2012 SRJC P1 Q1
The graph of $y=\frac{2}{1+x}$ for $x\ge 0$, is shown in the diagram below. Region $R$ is bounded by the $x$-axis, the $y$-axis, the line $x=1$ and the curve $y=\frac{2}{1+x}$. The area of region $R$ may be approximated by the total area, $A$, of $n$ rectangles, each of width $\frac{1}{n}$, as shown in the diagram.
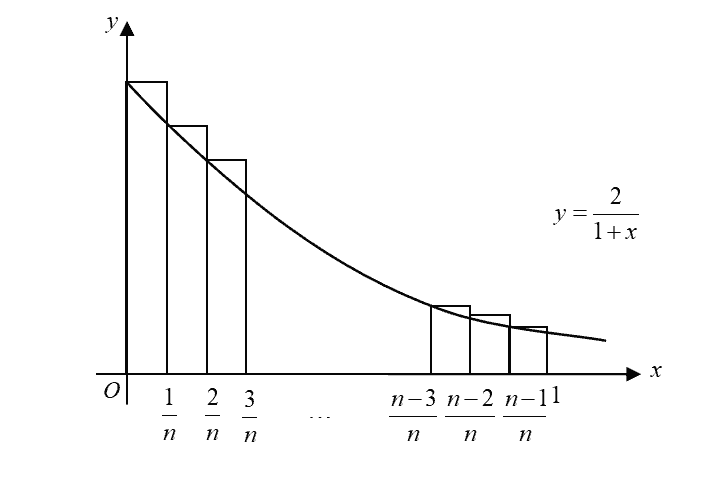
(i)
Show that $A=\sum\limits_{r=0}^{n-1}{\frac{2}{n+r}}$.
[2]
(ii)
By considering the exact area of region $R$, show that $\sum\limits_{r=0}^{n-1}{\frac{1}{n+r}}>\ln 2$.
[2]
Suggested Handwritten and Video Solutions
Share with your friends!
WhatsApp
Telegram
Facebook