A-Level H2 Math | 5 Essential Questions
Applications of Integration
Integration is a very useful extension of differentiation and relatively easy to understand. They are also known as the opposite of the derivatives. The definite integral is a powerful concept used to represent the area under a curve, which turns out to be useful in a lot of calculations.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2013 RVHS Promo Q3
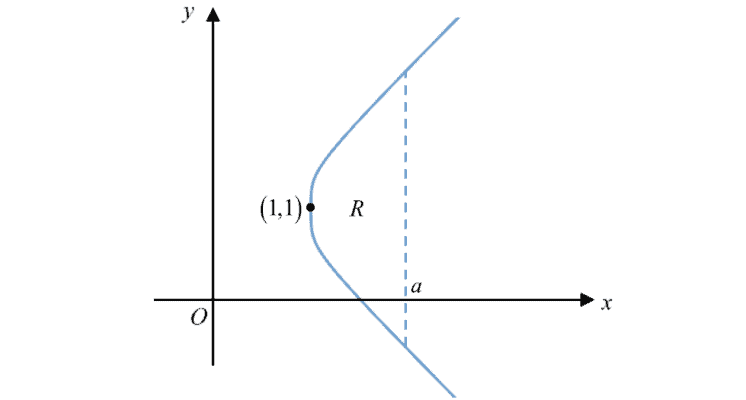
The diagram shows the sketch of the curve $C$, ${{\left( y-1 \right)}^{2}}=x\sqrt{{{x}^{2}}-1}$, with the vertex at $\left( 1,1 \right)$.
(i)
Write down the equation of the graph when $C$ is translated $1$ unit in the negative $y$-direction.
[1]
(i) Write down the equation of the graph when $C$ is translated $1$ unit in the negative $y$-direction.
[1]
(ii)
The shaded region $R$, bounded by $C$ and the vertical line, $x=a$, is rotated through $\pi $ radians about the line $y=1$. By using the substitution $u=\sqrt{{{x}^{2}}-1}$, or otherwise, find the exact volume obtained in terms of $a$.
[5]
(ii) The shaded region $R$, bounded by $C$ and the vertical line, $x=a$, is rotated through $\pi $ radians about the line $y=1$. By using the substitution $u=\sqrt{{{x}^{2}}-1}$, or otherwise, find the exact volume obtained in terms of $a$.
[5]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
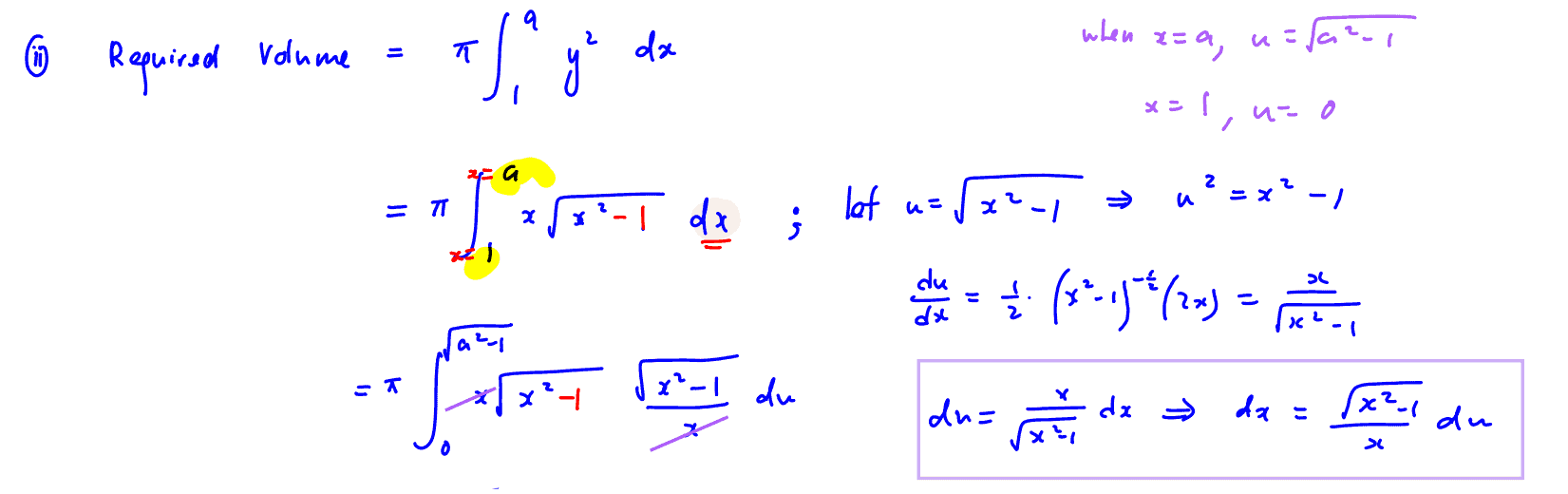
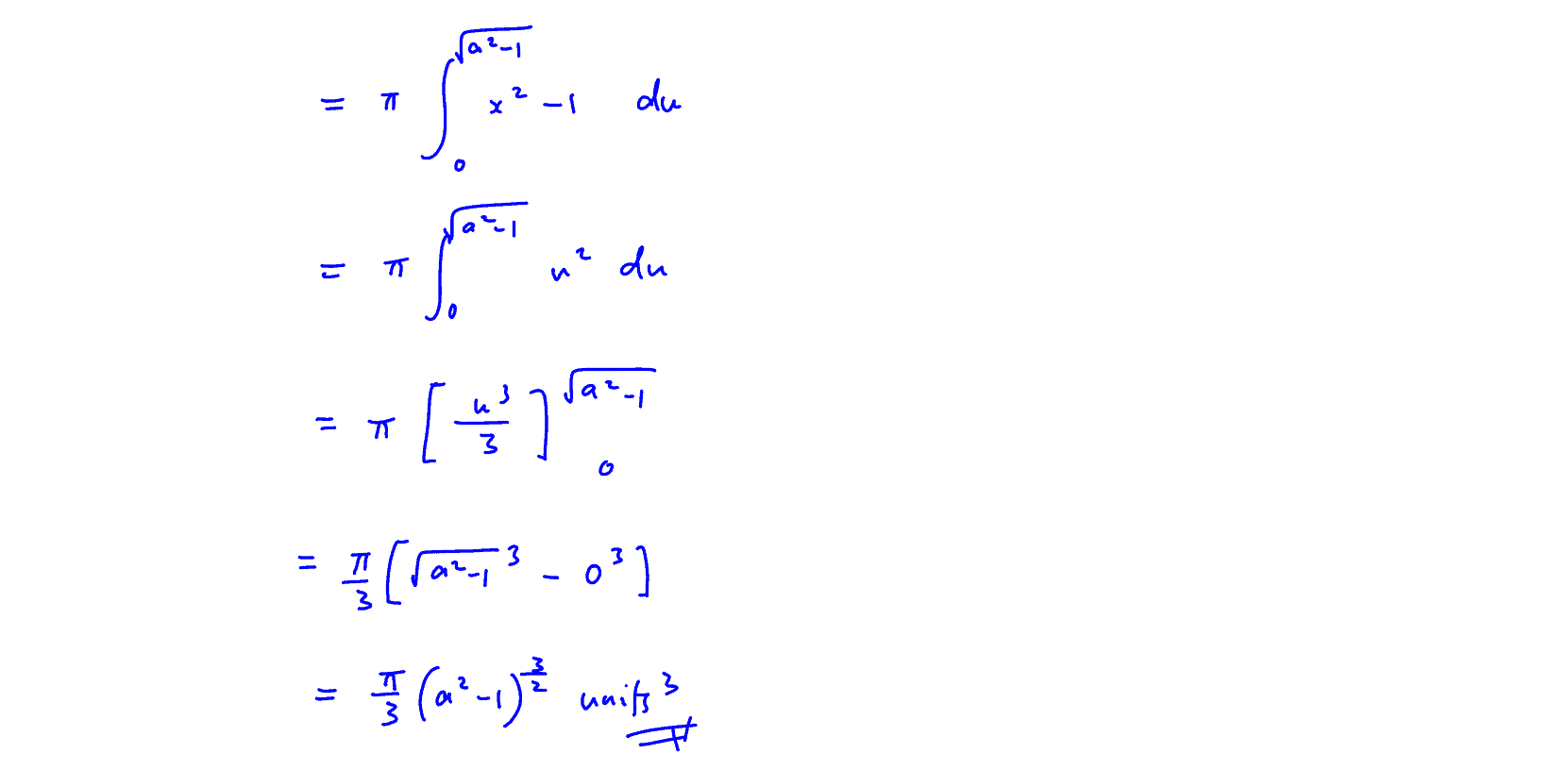
- (i)
- (ii)
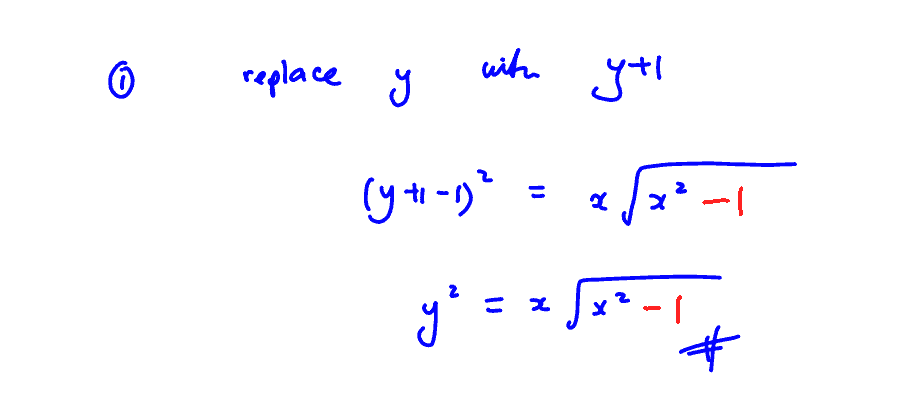
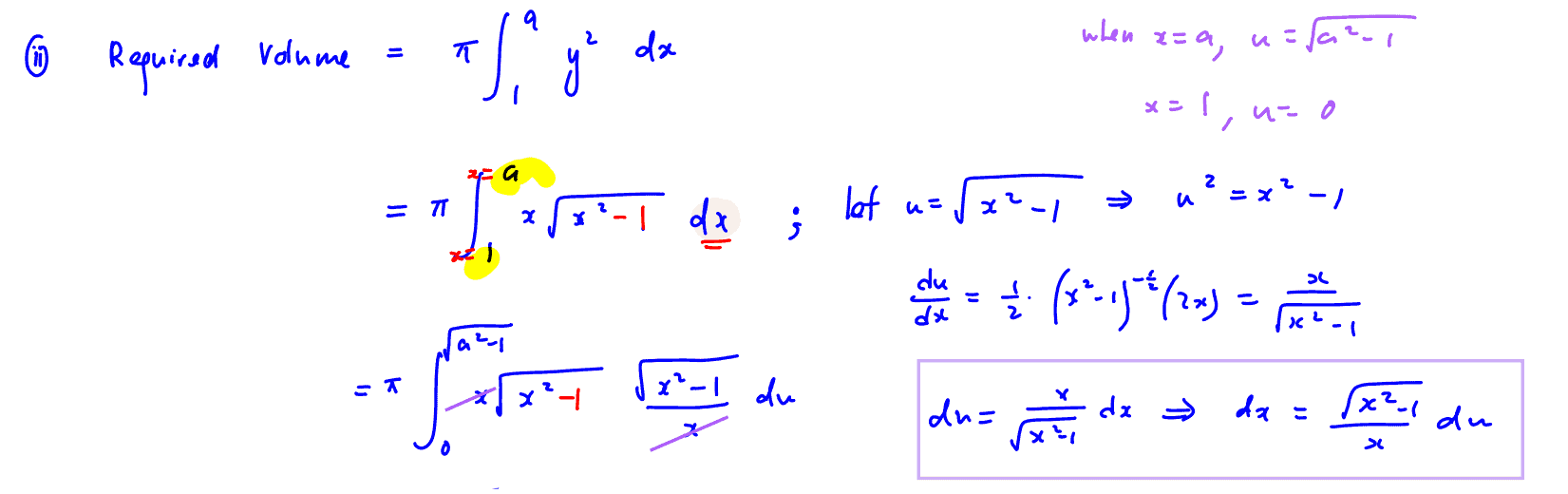
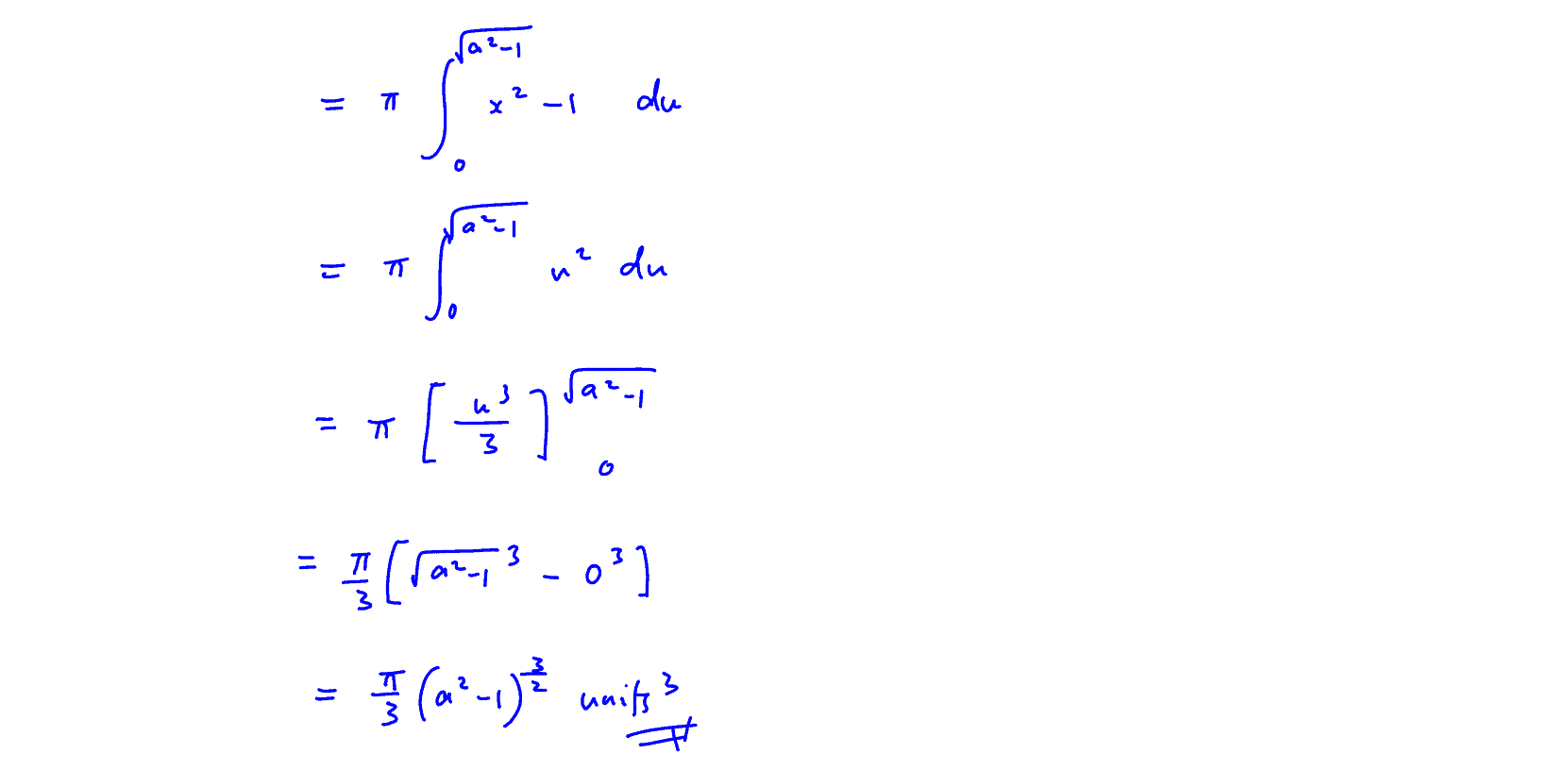
Share with your friends!
2013 AJC Promo Q8 (b)
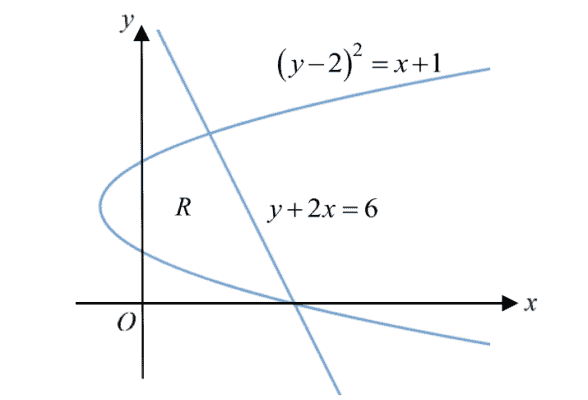
The diagram shows a shaded region $R$ bounded by the curve ${{\left( y-2 \right)}^{2}}=x+1$ and the line $y+2x=6$.
[4]
Suggested Handwritten and Video Solutions
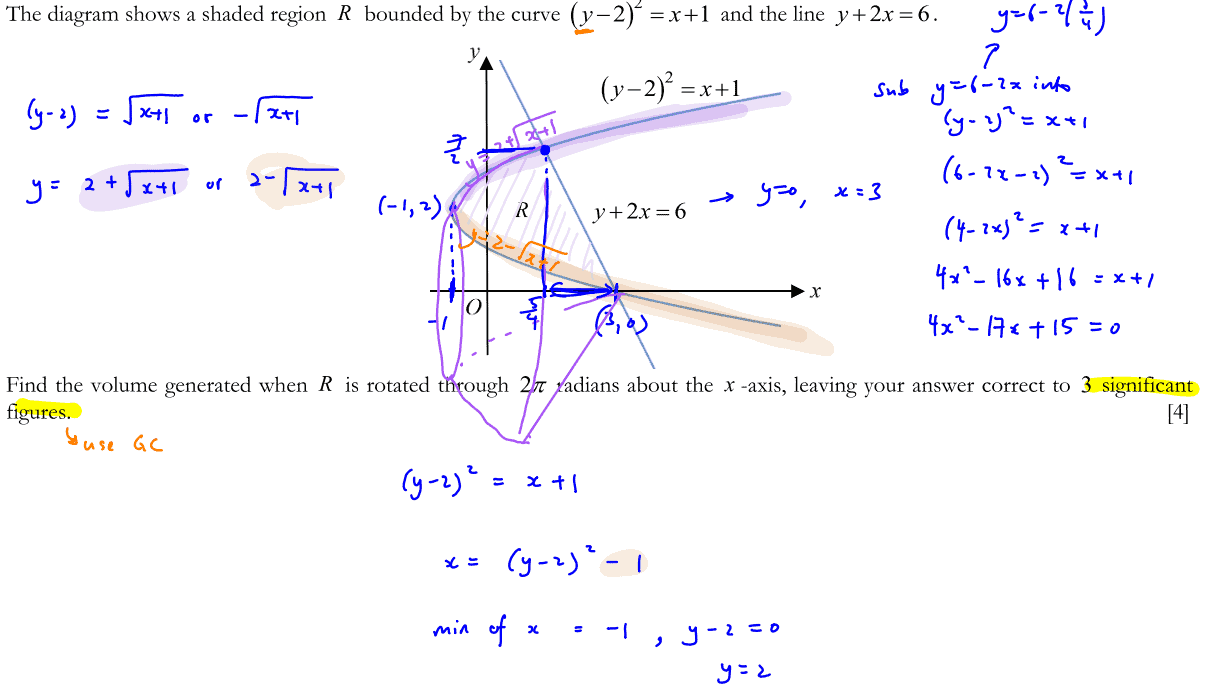
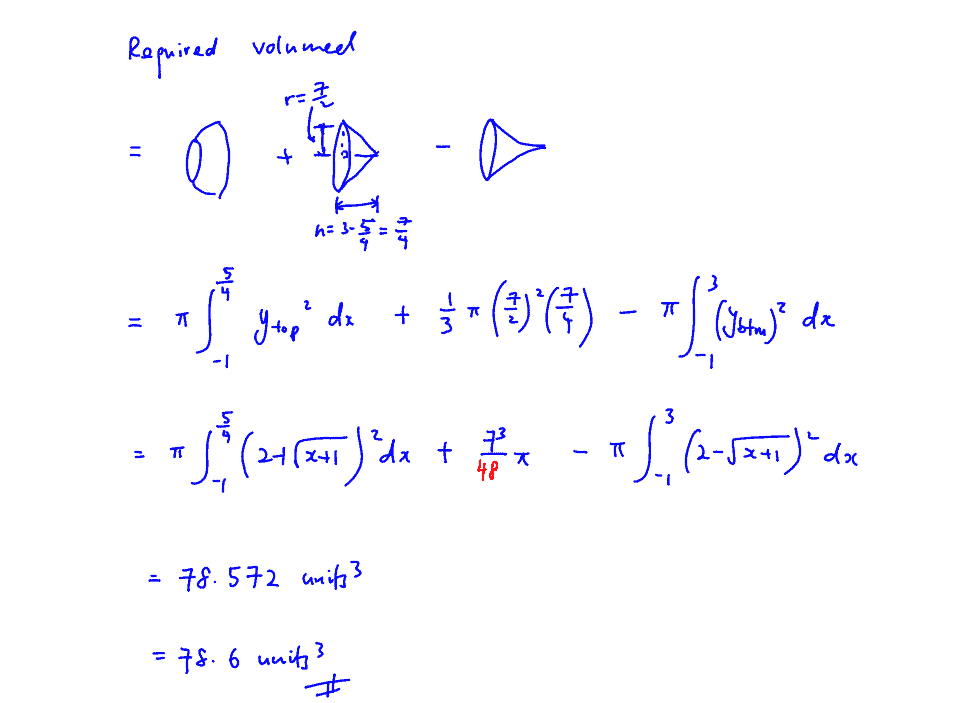
Share with your friends!
2017 YJC P1 Q9
(a)
By using the substitution $x=3\sec \theta $, evaluate $\int_{3\sqrt{2}}^{6}{\frac{3x+1}{\sqrt{{{x}^{2}}-9}}\text{d}x}$ exactly.
[5]
(a) By using the substitution $x=3\sec \theta $, evaluate $\int_{3\sqrt{2}}^{6}{\frac{3x+1}{\sqrt{{{x}^{2}}-9}}\text{d}x}$ exactly.
[5]
(b)
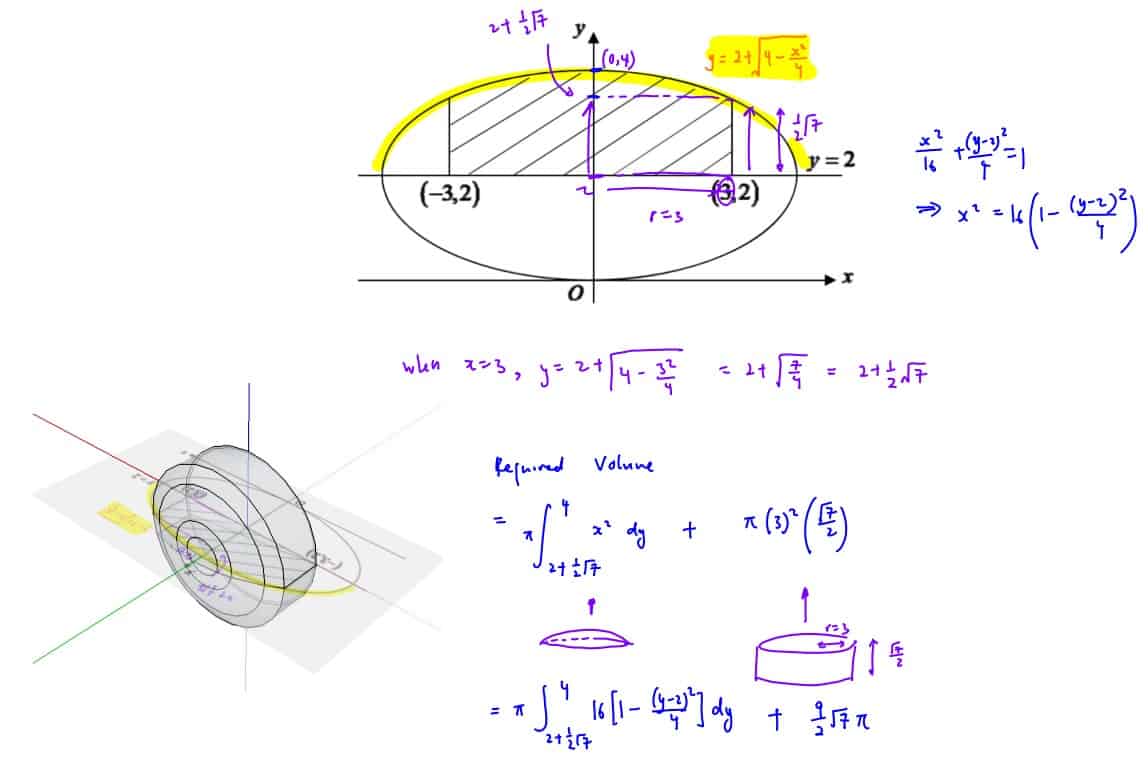
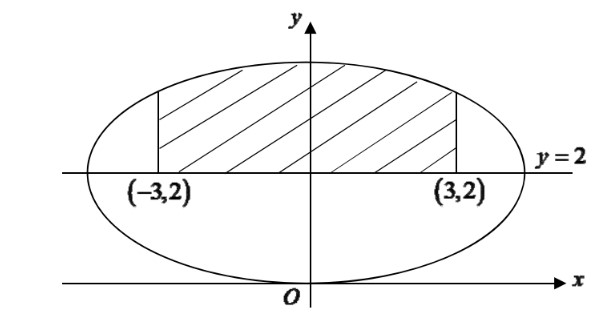 The diagram shows an ellipse with equation $\frac{{{x}^{2}}}{16}+\frac{{{\left( y-2 \right)}^{2}}}{4}=1$.
The diagram shows an ellipse with equation $\frac{{{x}^{2}}}{16}+\frac{{{\left( y-2 \right)}^{2}}}{4}=1$. (b)
The diagram shows an ellipse with equation $\frac{{{x}^{2}}}{16}+\frac{{{\left( y-2 \right)}^{2}}}{4}=1$.
(i)
Find the area of the shaded region, giving your answer correct to $3$ decimal places.
[2]
[2]
(ii)
Find the exact volume of the solid generated when the shaded region is rotated $180{}^\circ $ about the $y$-axis.
[4]
(ii) Find the exact volume of the solid generated when the shaded region is rotated $180{}^\circ $ about the $y$-axis.
[4]
Suggested Handwritten and Video Solutions
- (a)
- (b) (i)
- (b) (ii)

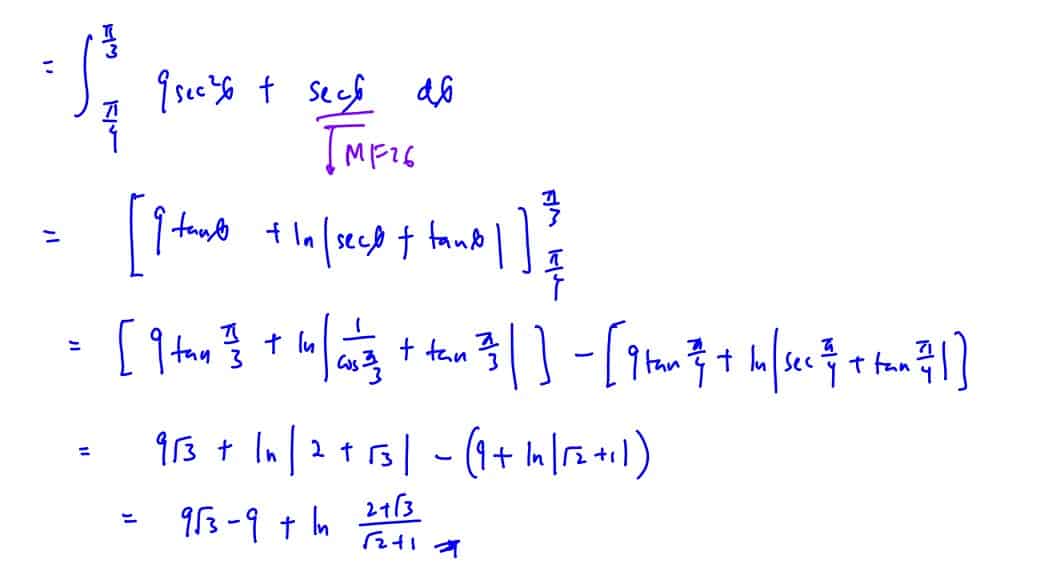
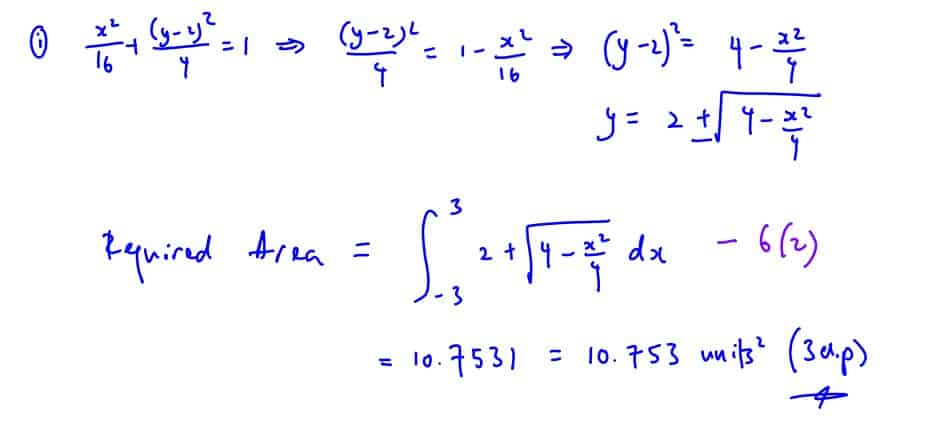
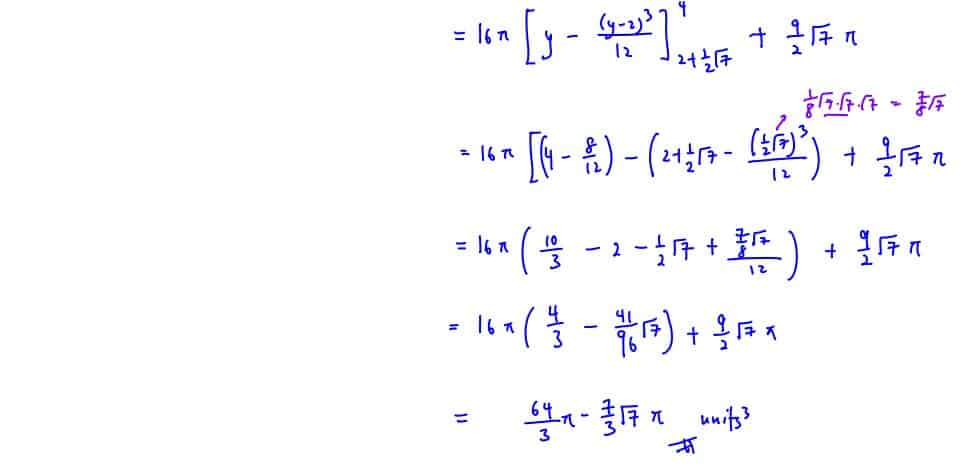
- (a)
- (b) (i)
- (b) (ii)

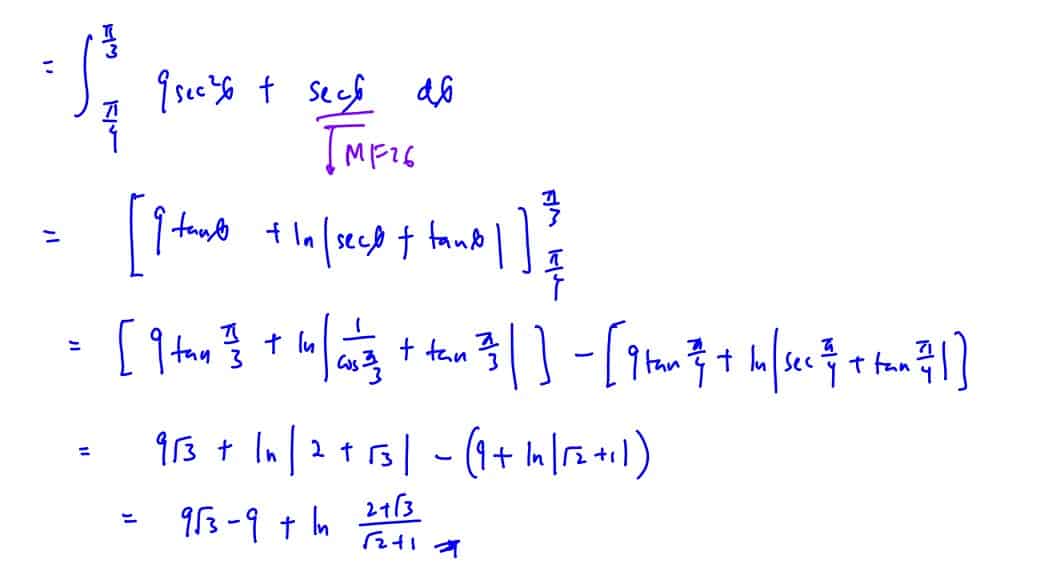
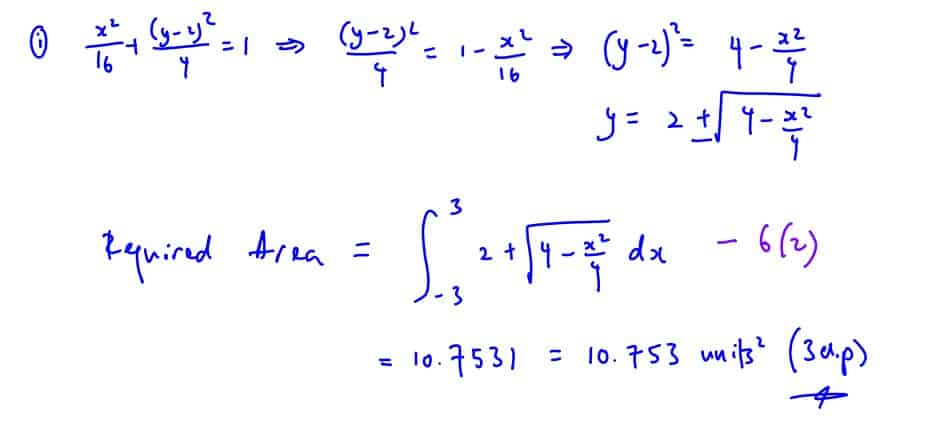

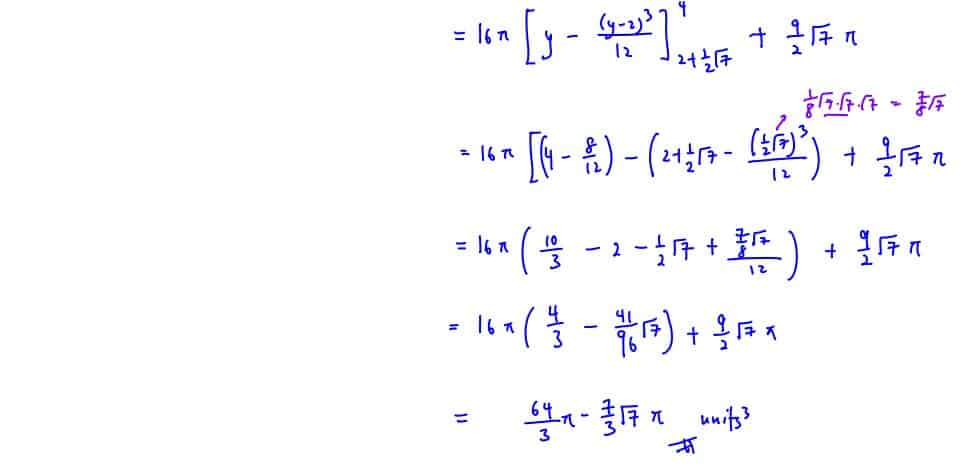
Share with your friends!
2020 ASRJC P2 Q4
(a)
Find $\int{\left( {{\cot }^{6}}2x+{{\cot }^{4}}2x-\sin \frac{x}{2}\sin \frac{3x}{2} \right)}\text{ d}x$.
[3]
(a) Find $\int{\left( {{\cot }^{6}}2x+{{\cot }^{4}}2x-\sin \frac{x}{2}\sin \frac{3x}{2} \right)}\text{ d}x$.
[3]
(b)
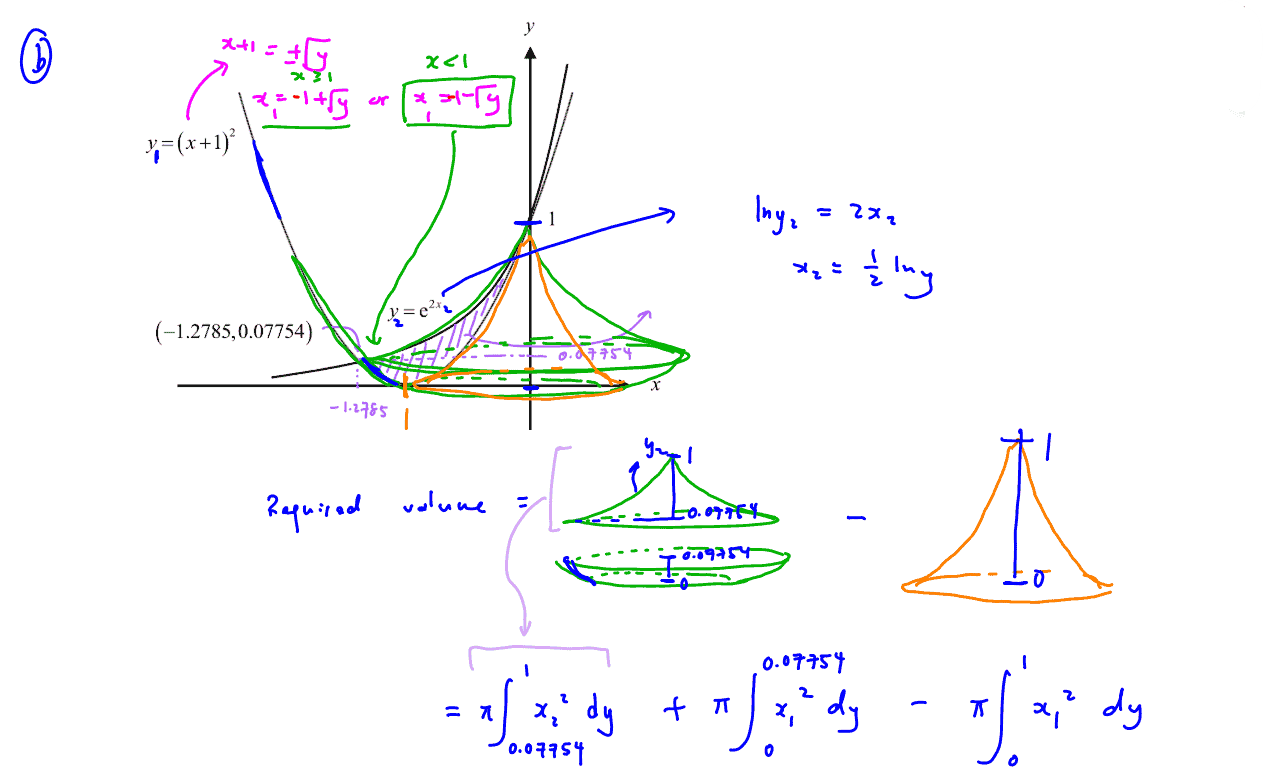
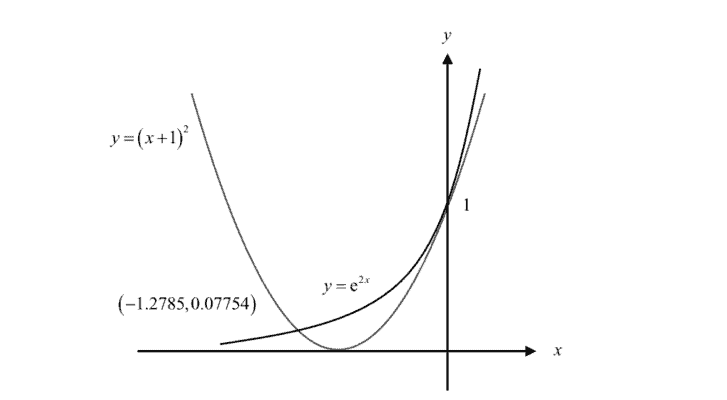 $R$ is the finite region bounded by the two curves $y={{\text{e}}^{2x}}$ and $y={{\left( x+1 \right)}^{2}}$.
Find the volume of the solid formed when $R$ is rotated through $2\pi $ radians about the $y$-axis, giving your answer correct to $4$ decimal places.
$R$ is the finite region bounded by the two curves $y={{\text{e}}^{2x}}$ and $y={{\left( x+1 \right)}^{2}}$.
Find the volume of the solid formed when $R$ is rotated through $2\pi $ radians about the $y$-axis, giving your answer correct to $4$ decimal places.
[3]
(b) The diagram shows the graphs of $y={{\text{e}}^{2x}}$ and $y={{\left( x+1 \right)}^{2}}$.
$R$ is the finite region bounded by the two curves $y={{\text{e}}^{2x}}$ and $y={{\left( x+1 \right)}^{2}}$.
Find the volume of the solid formed when $R$ is rotated through $2\pi $ radians about the $y$-axis, giving your answer correct to $4$ decimal places.
[3]
(c)
$x=2\left( \sin \frac{t}{2}-\cos \frac{t}{2} \right)$, $y=\sin \frac{t}{2}+\cos \frac{t}{2}$, for $-\frac{3\pi }{2}\le t\le -\frac{\pi }{2}$.
The line $L$ with equation $y=-2x-5$ meets the curve $C$ at the point $\left( -2,\,-1 \right)$. $S$ is the region enclosed by line $L$, curve $C$and the $x$-axis as shown in the diagram below.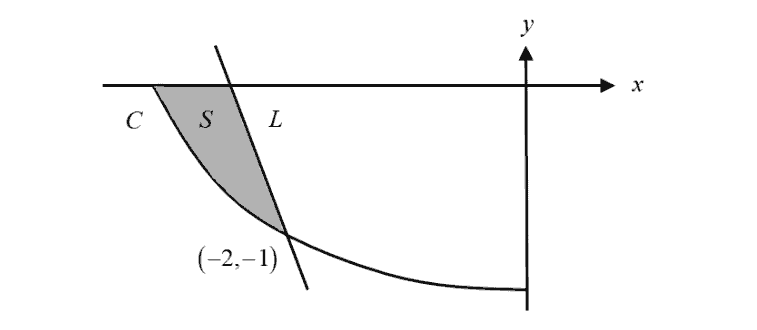
(c) A curve $C$ has parametric equations
$x=2\left( \sin \frac{t}{2}-\cos \frac{t}{2} \right)$, $y=\sin \frac{t}{2}+\cos \frac{t}{2}$, for $-\frac{3\pi }{2}\le t\le -\frac{\pi }{2}$.
The line $L$ with equation $y=-2x-5$ meets the curve $C$ at the point $\left( -2,\,-1 \right)$.
$S$ is the region enclosed by line $L$, curve $C$and the $x$-axis as shown in the diagram below.
(i)
Show that the x-intercept of curve $C$ is $-2\sqrt{2}$.
[2]
(i) Show that the x-intercept of curve $C$ is $-2\sqrt{2}$.
[2]
(ii)
Find the exact area of $S$.
[6]
(ii) Find the exact area of $S$.
[6]
Suggested Handwritten and Video Solutions
- (a)
- (b)
- (c) (i)
- (c) (ii)
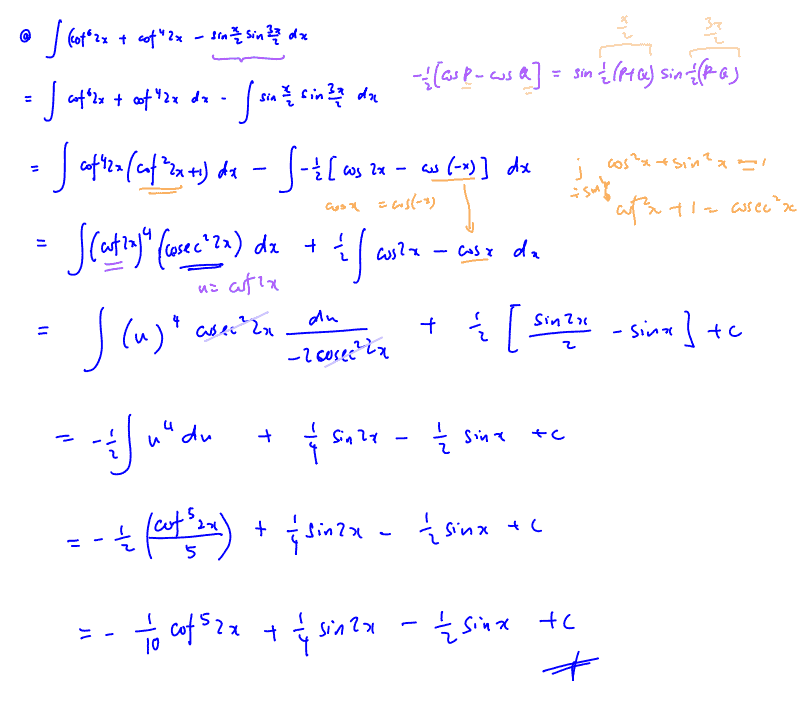
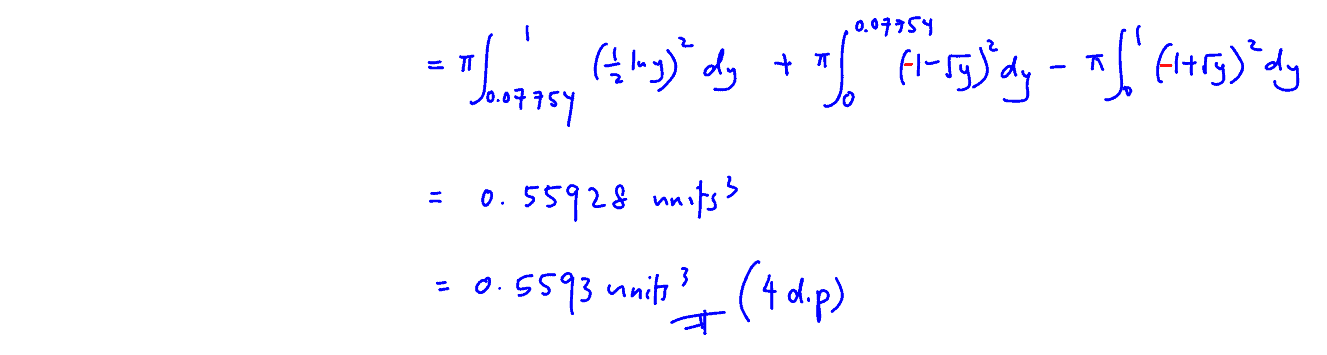
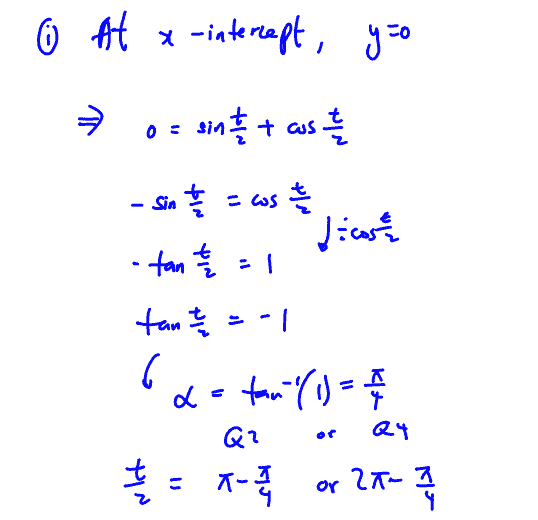
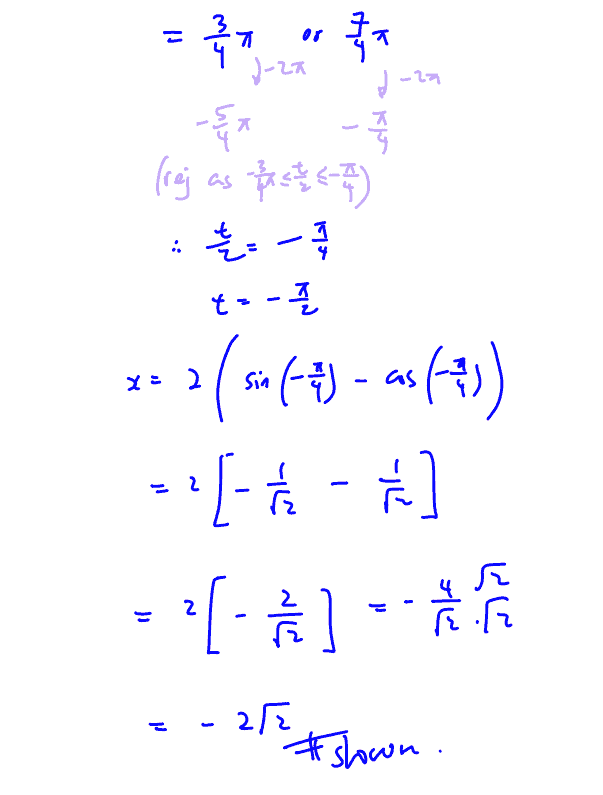
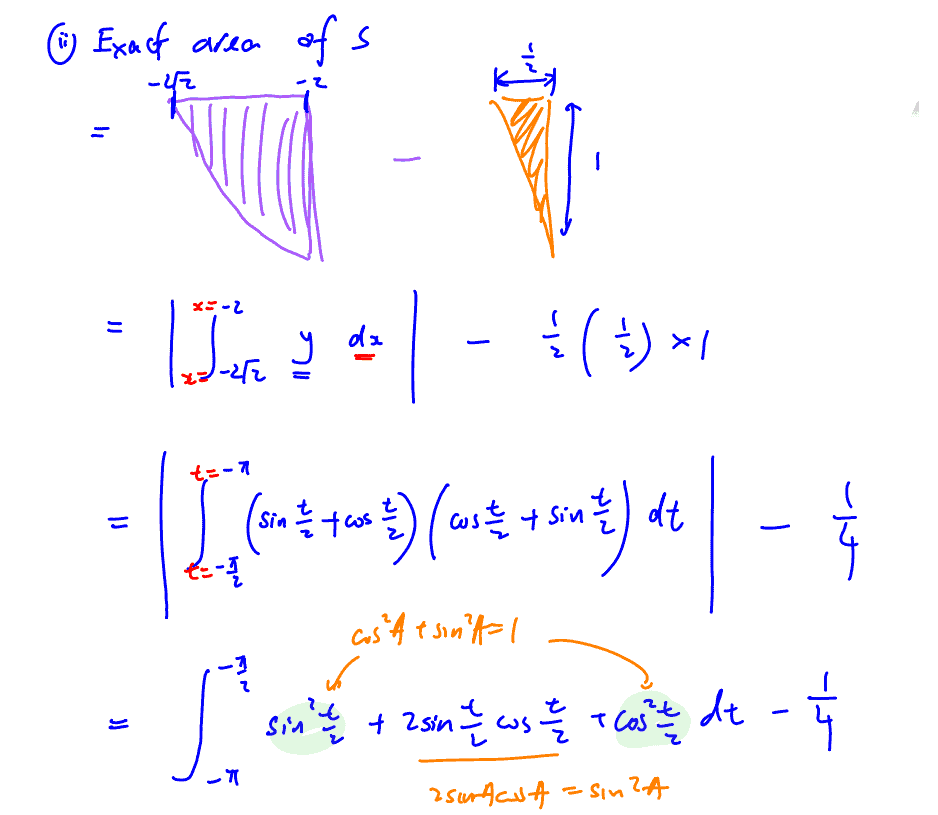
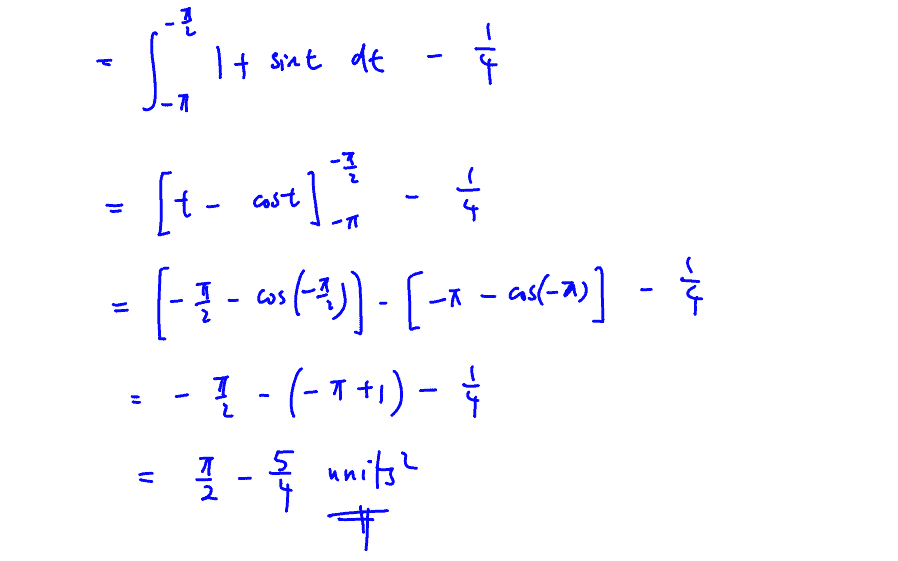
- (a)
- (b)
- (c) (i)
- (c) (ii)
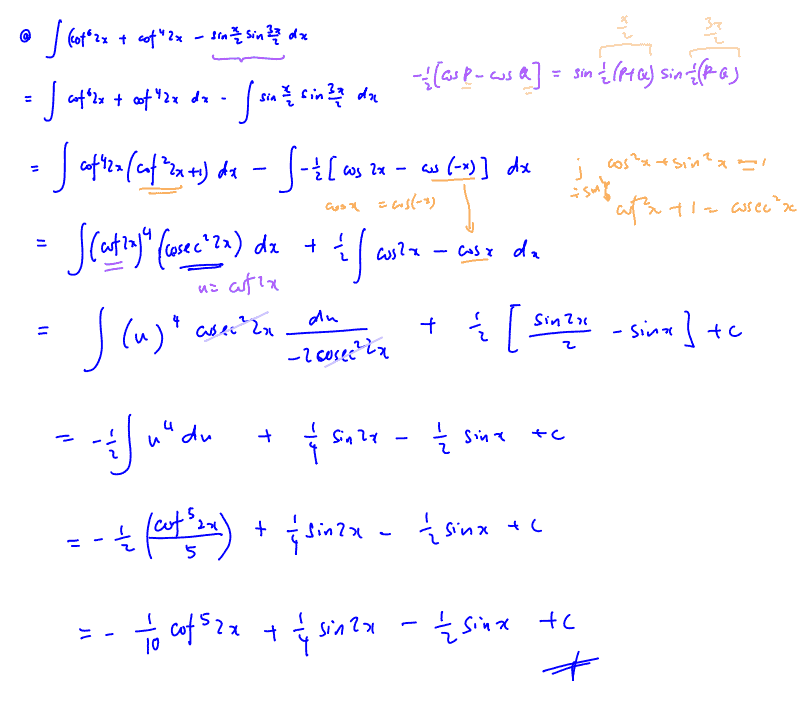

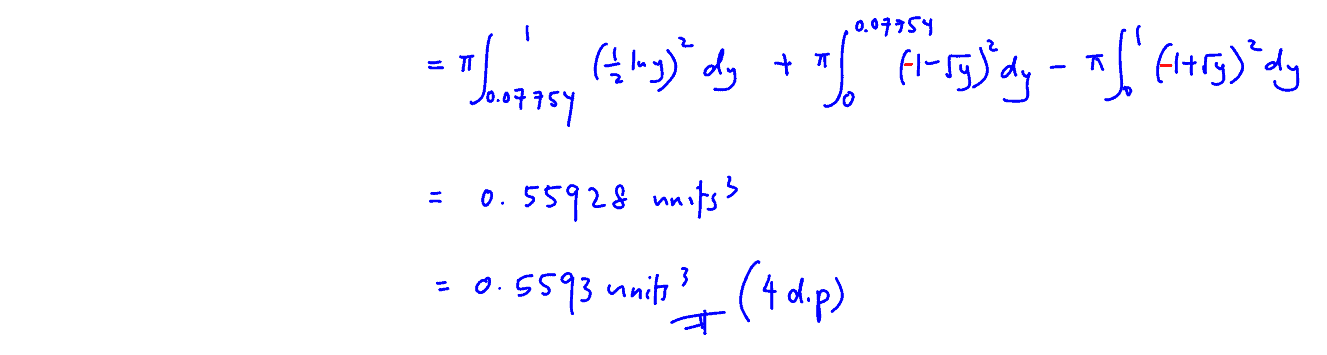
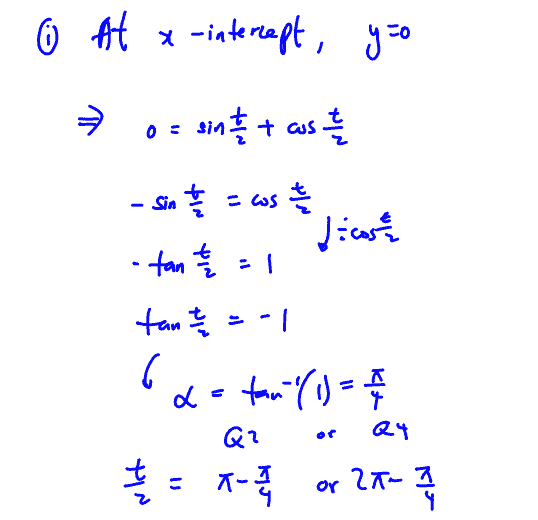
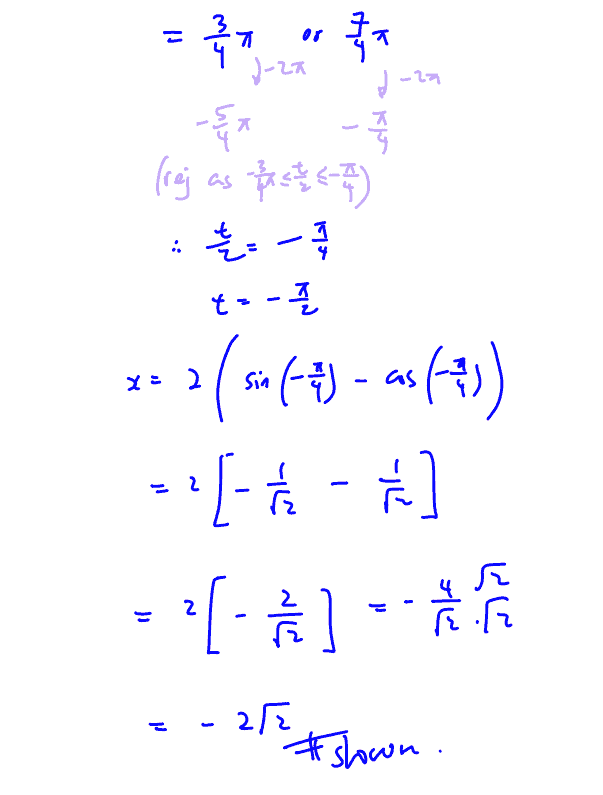
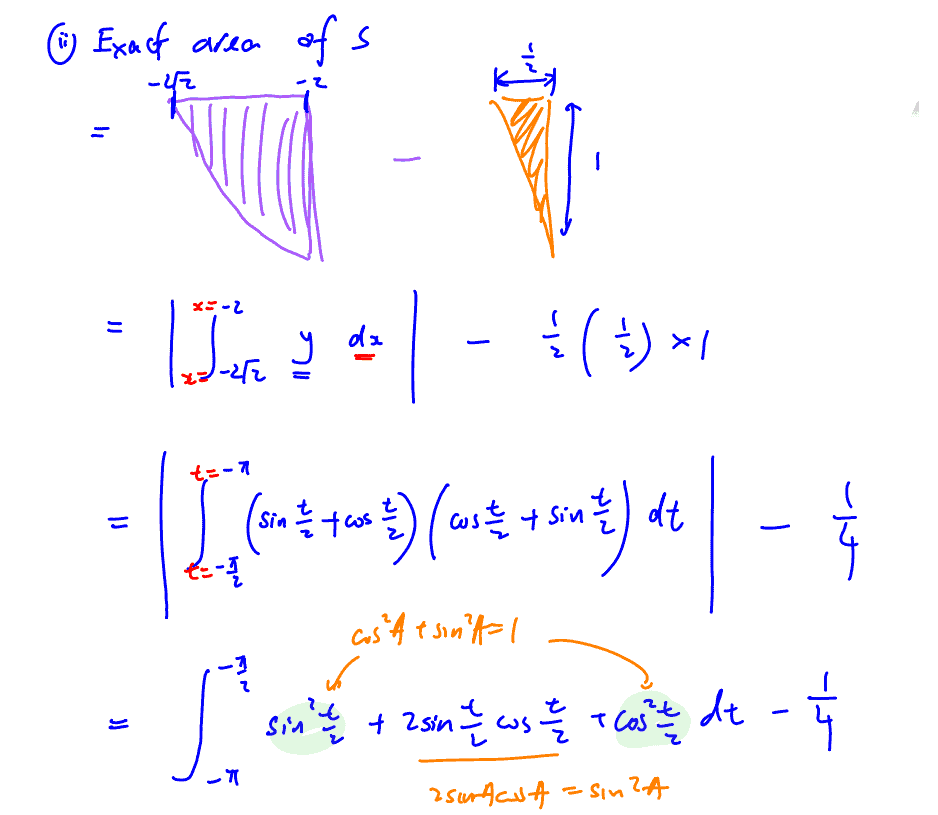
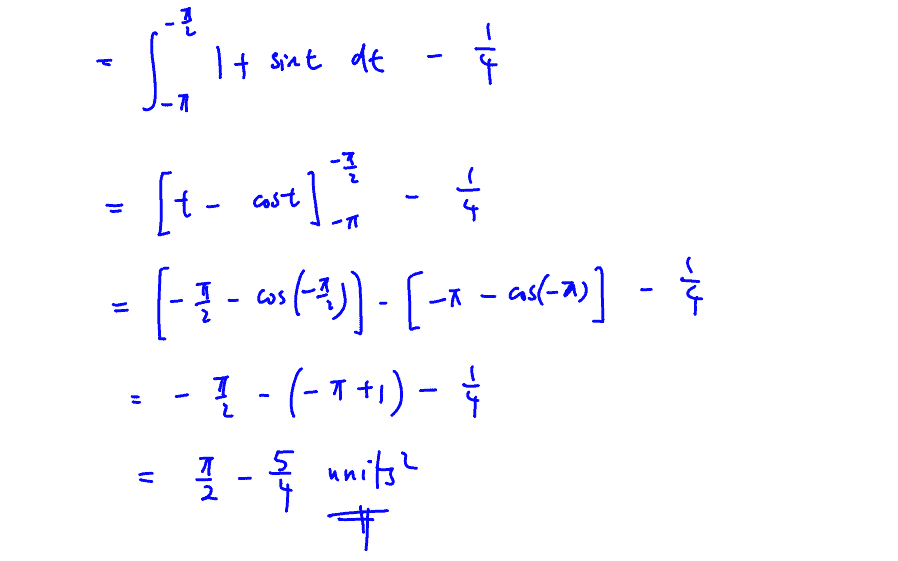
Share with your friends!
2011 CJC P1 Q8
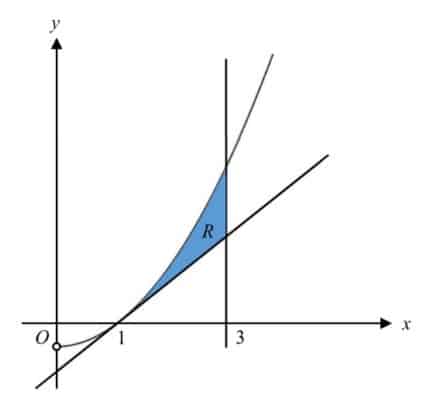
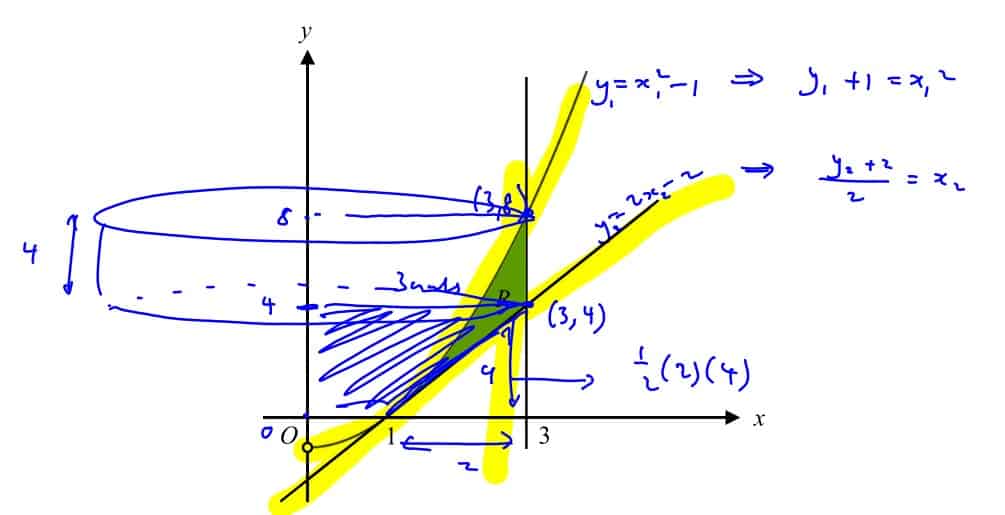
The diagram below shows the curve with equation $y={{x}^{2}}-1$, $x>0$ and the tangent $y=2x-2$ to the curve at the point $(1,0)$.
(i)
Write down the coordinates of the point where this tangent meets the line $x=3$.
[1]
(i) Write down the coordinates of the point where this tangent meets the line $x=3$.
[1]
The region, $R$, shaded in the diagram, is bounded by the curve, the tangent to the curve at $(1,0)$ and the line $x=3$.
Find
(ii)
the area of $R$,
[2]
(ii) the area of $R$,
[2]
(iii)
the exact volume of the solid of revolution obtained when $R$ is rotated through $2\pi $ radians about the $y$-axis.
[4]
(iii) the exact volume of the solid of revolution obtained when $R$ is rotated through $2\pi $ radians about the $y$-axis.
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
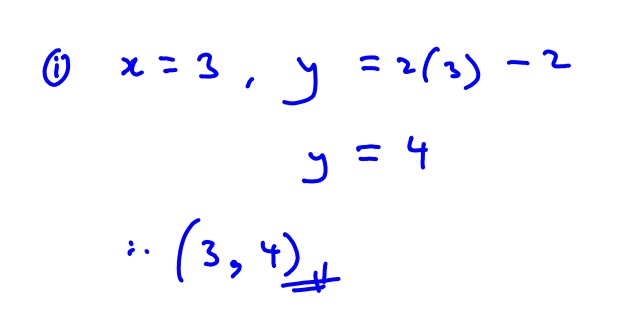
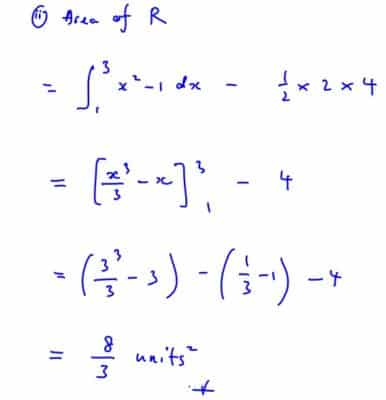

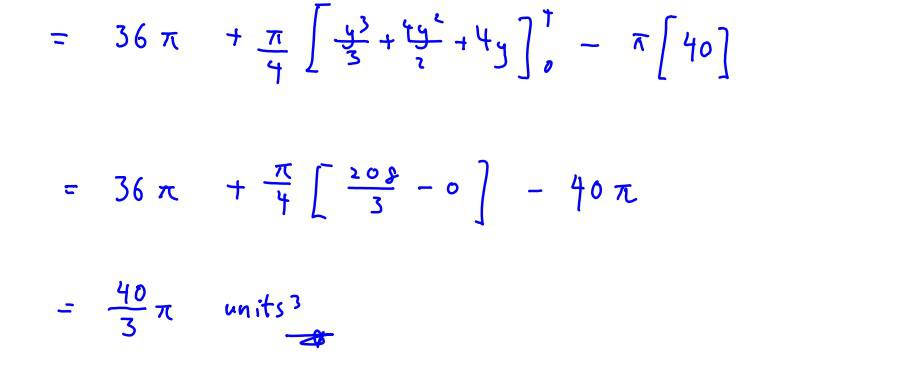
- (i)
- (ii)
- (iii)
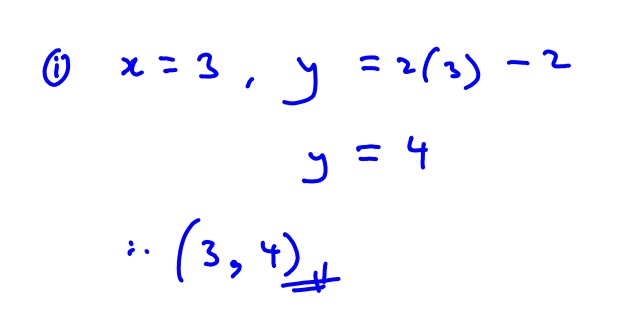
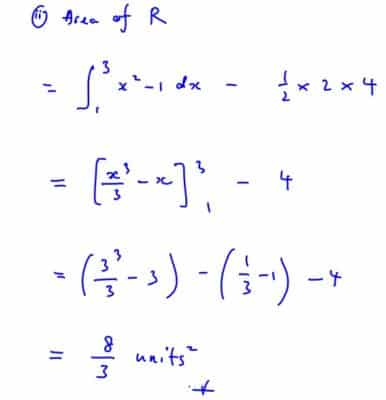


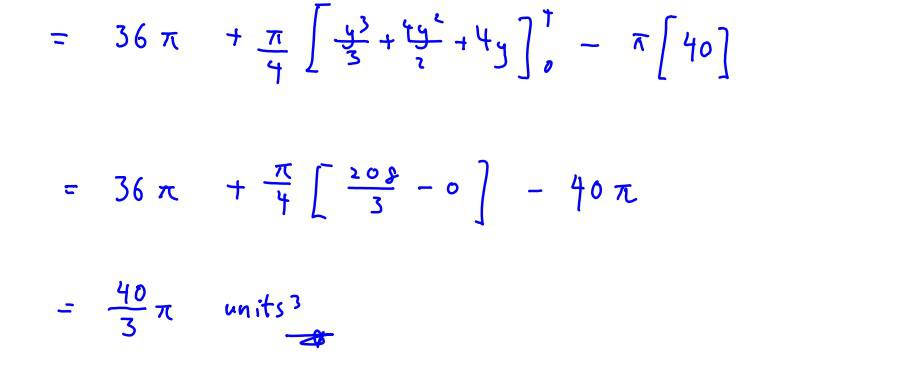
Share with your friends!
A curve $C$ has equation $y=\frac{1}{\sqrt{4-{{x}^{2}}}}$ for $-1\le x\le 1$. The region $R$ is enclosed by $C$, the $x$- axis and the lines $x=-1$ and $x=1$.
(i)
Find the exact value of the area of $R$.
[3]
(ii)
Find the exact value of the volume generated when $R$ is rotated through two right angles about the $x$- axis.
[3]
(iii)
Show that the volume generated when $R$ is rotated through two right angles about the $y$- axis is $\pi \,(4-2\sqrt{3})$.
[4]
Download Applications of Integration Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!