A-Level H2 Math | 5 Essential Questions
Binomial Distribution
The binomial distribution is a discrete probability distribution that gives only two possible results in an experiment, hence the name “binomial”. In order to use a binomial distribution, there must be some assumptions made about the experiment itself.
- Each trial of the experiment must be independent.
- There must be only two possible outcomes of each trial.
- The probability of success must be constant in every trial.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2015 DHS P2 Q7 [Modified]
Data is transmitted in bytes, where each byte consists of $8$ bits. The probability of a bit being corrupted during its transmission is $0.03$. A byte is considered ‘corrupted’ if it contains at least $2$ corrupted bits.
Assume that all bits are not corrupted prior to their transmission.
(i)
Find the probability that a randomly chosen byte is corrupted during its transmission.
(i) Find the probability that a randomly chosen byte is corrupted during its transmission.
(ii)
Given that a randomly chosen byte is not corrupted during its transmission, find the probability that it contains no corrupted bits.
(ii) Given that a randomly chosen byte is not corrupted during its transmission, find the probability that it contains no corrupted bits.
(iii)
Find the probability that between $5$ and $10$ bytes are corrupted during the transmission of $100$ bytes.
(iii) Find the probability that between $5$ and $10$ bytes are corrupted during the transmission of $100$ bytes.
In another transmission system, the probability of having at least $3$ corrupted bytes during the transmission of $20$ bytes is $0.85$. Find the probability that a bit is corrupted during its transmission.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- -
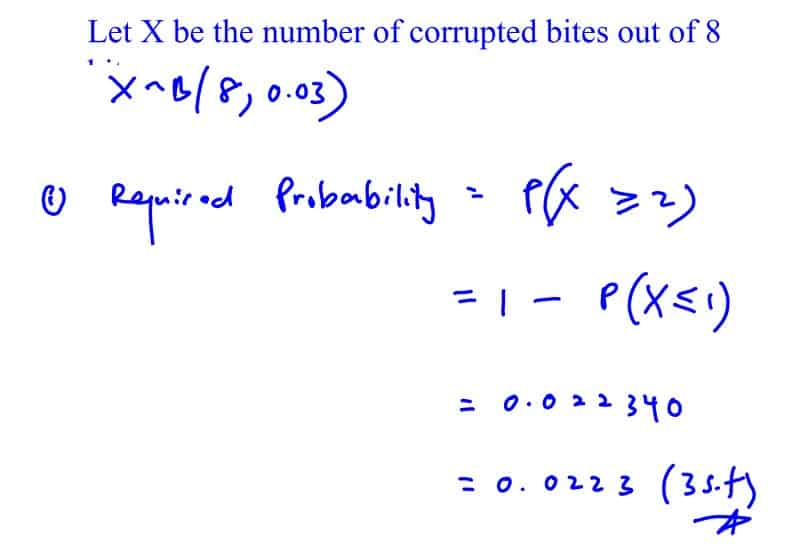
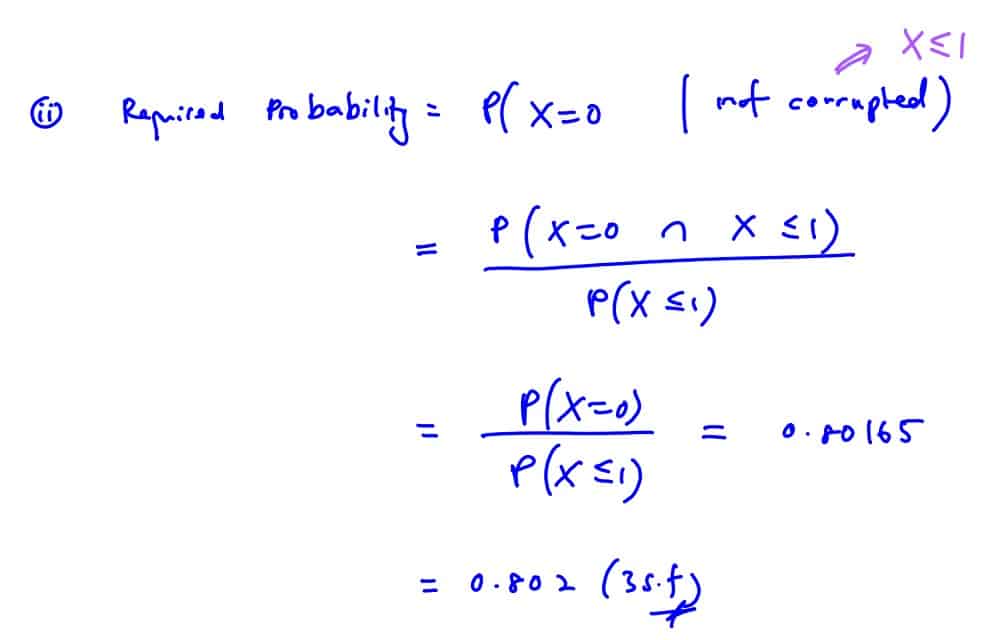


- (i)
- (ii)
- (iii)
- -
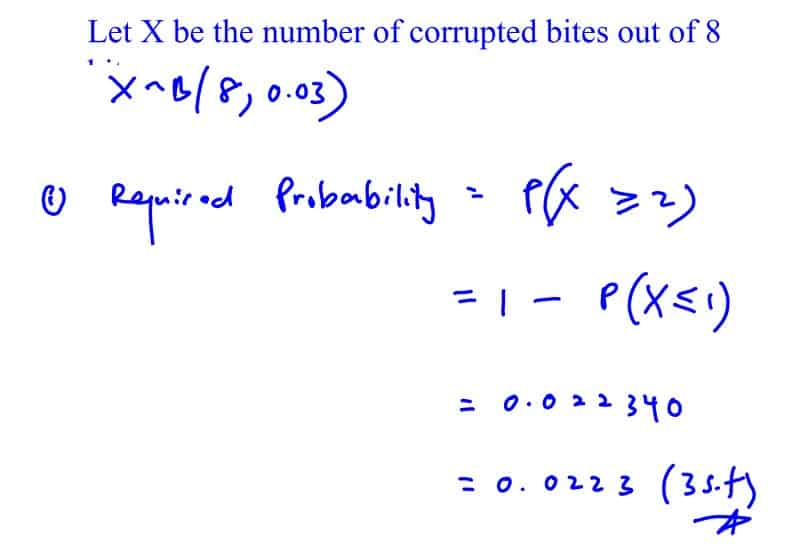
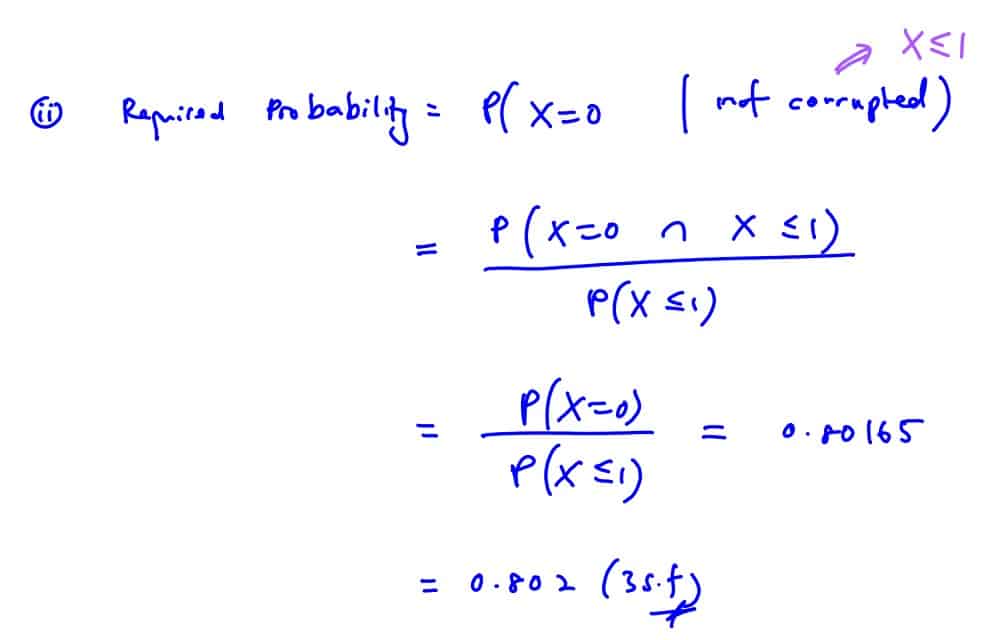


2017 VJC J2 MYE P1 Q11
A trial for a new treatment for a particular disease is to be carried out. A sample of $n$ patients suffering from this disease is taken and these patients are invited to take part in the trial. The number of patients in the sample who accept the invitation is denoted by $X$.
(i)
State, in context, two assumptions needed for $X$ to be well modelled by a binomial distribution.
[2]
(i) State, in context, two assumptions needed for $X$ to be well modelled by a binomial distribution.
[2]
Assume now that $X$ has the distribution $\text{B}(10,\,0.25)$.
(ii)
Find the most probable number of patients who accept the invitation.
[2]
(ii) Find the most probable number of patients who accept the invitation.
[2]
(iii)
Find the probability that exactly $6$ patients accept the invitation given that at least $1$ patient accepts the invitation.
[2]
(iii) Find the probability that exactly $6$ patients accept the invitation given that at least $1$ patient accepts the invitation.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)


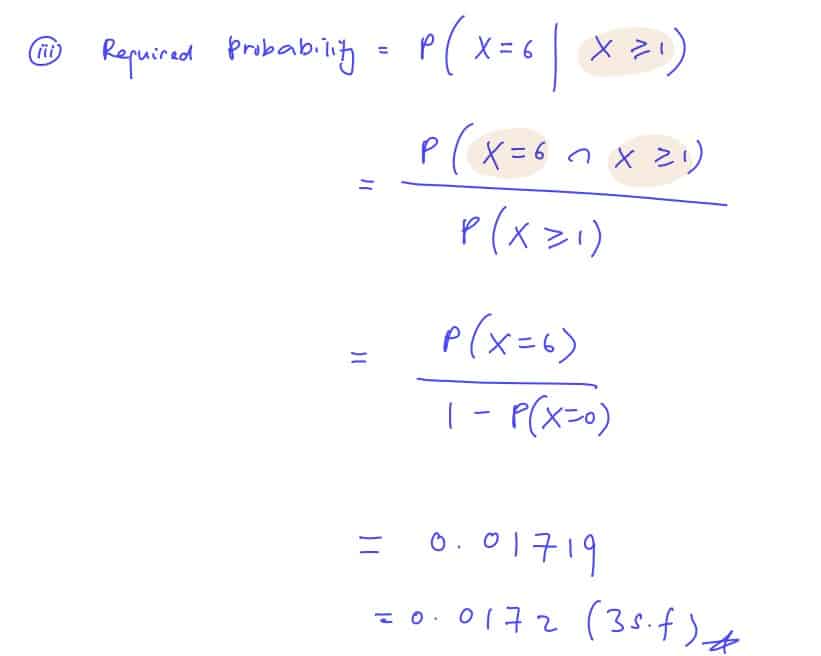
- (i)
- (ii)
- (iii)


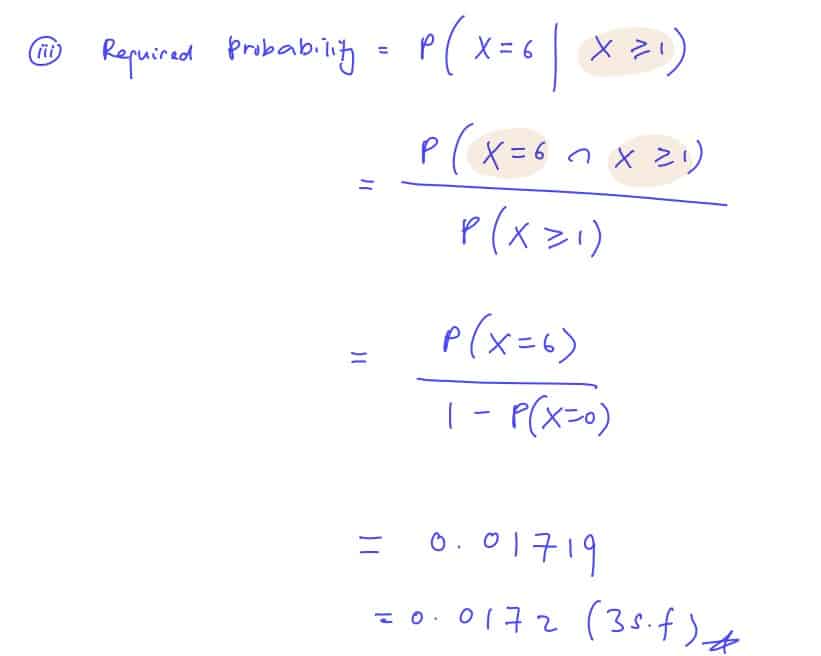
Share with your friends!
These Ten-Year-Series (TYS) worked solutions with video explanations for 1982 A Level H2 Mathematics Paper 1 Question 13 are suggested by Mr Gan. For any comments or suggestions please contact us at support@timganmath.edu.sg.
N1982 P1 Q13
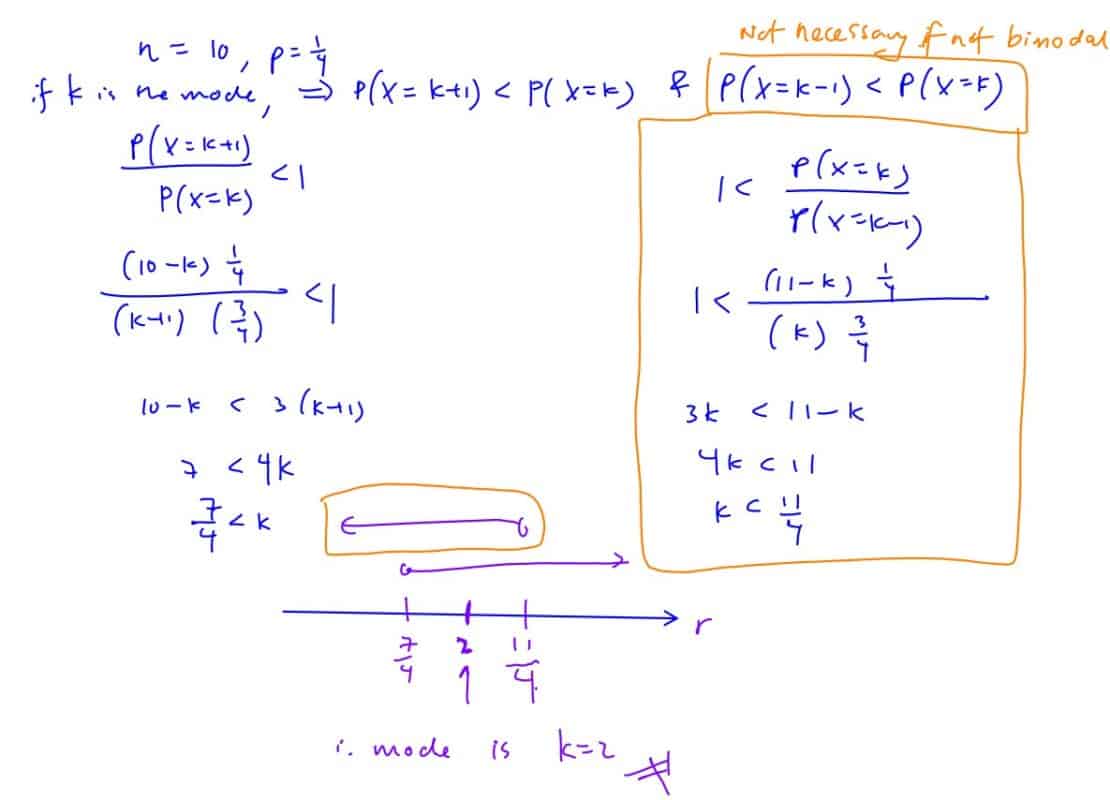
The random variable $X$ is the number of successes in $n$ independent trials of an experiment in which the probability of a success in any one trial is $p$.
Show that
$\frac{\text{P}\left( X=k+1 \right)}{\text{P}\left( X=k \right)}=\frac{\left( n-k \right)p}{\left( k+1 \right)\left( 1-p \right)},k=0,1,2,…,\left( n-1 \right)$
Find the most probable number of success when $n=10$ and $p=\frac{1}{4}$.
Suggested Handwritten and Video Solutions

Share with your friends!
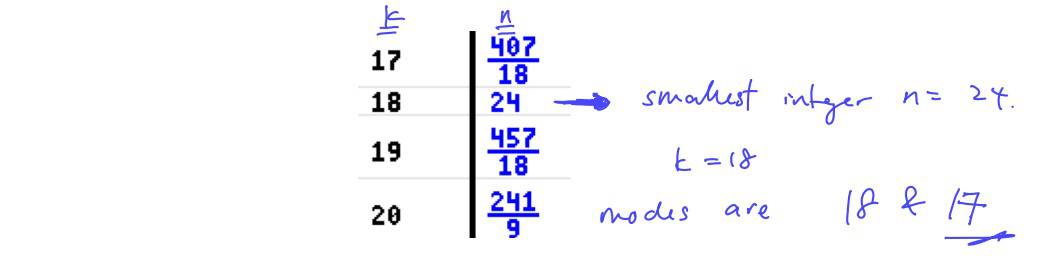
2018 ACJC MYE Q8
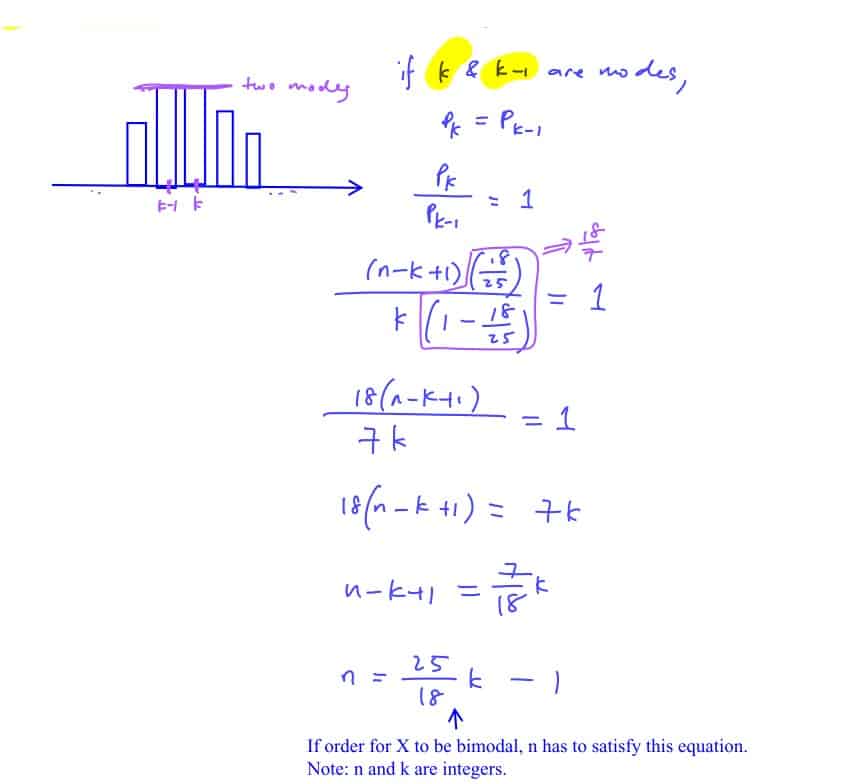
The random variable $X$ is the number of successes in $n$ independent trials of an experiment in which the probability of a success at any trial is $p$.
Denoting $\text{P}(X=k)$ by ${{p}_{k}}$, it is given that $\frac{{{p}_{k}}}{{{p}_{k-1}}}=\frac{(n-k+1)p}{k(1-p)}$, $k=1$, $2$, …, $n$.
A distribution is said to be bimodal if it has two modes.
Find the least value of $n$, and the corresponding modes of $X$, given that $X$ is bimodal and that $p=\frac{18}{25}$.
Suggested Handwritten and Video Solutions
Share with your friends!
2019 SAJC P2 Q10
A factory manufactures a large number of erasers in a variety of colours. Each box of erasers contains $36$ randomly chosen erasers. On average, $20$% of erasers in the box are blue.
(i)
State, in context, two assumptions needed for the number of blue erasers in a box to be well modelled by a binomial distribution.
[2]
(i) State, in context, two assumptions needed for the number of blue erasers in a box to be well modelled by a binomial distribution.
[2]
(ii)
Find the probability that a randomly chosen box of erasers contain at most six blue erasers.
[1]
(ii) Find the probability that a randomly chosen box of erasers contain at most six blue erasers.
[1]
$200$ randomly chosen boxes are packed into a carton. A carton is considered acceptable if at least $40$% of the boxes contain at most six blue erasers each.
(iii)
Find the probability that a randomly chosen carton is acceptable.
[3]
(iii) Find the probability that a randomly chosen carton is acceptable.
[3]
The cartons are exported by sea. Over a one-year period, there are $30$ shipments of $150$ cartons each.
(iv)
Using a suitable approximation, find the probability that the mean number of acceptable cartons per shipment for the year is less than $80$.
[3]
(iv) Using a suitable approximation, find the probability that the mean number of acceptable cartons per shipment for the year is less than $80$.
[3]
The owner decided to change the proportion of blue erasers to $p$. A box of erasers is chosen.
(v)
Write down in terms of $p$, the probability that the box contains exactly one blue eraser.
[1]
(v) Write down in terms of $p$, the probability that the box contains exactly one blue eraser.
[1]
(vi)
The probability that a box contains exactly one blue eraser is twice the probability that the box contains exactly two blue erasers. Write an equation in terms of $p$, and hence find the value of $p$.
[2]
(vi) The probability that a box contains exactly one blue eraser is twice the probability that the box contains exactly two blue erasers. Write an equation in terms of $p$, and hence find the value of $p$.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
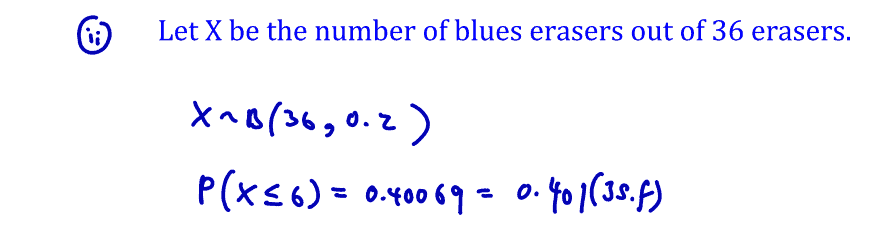


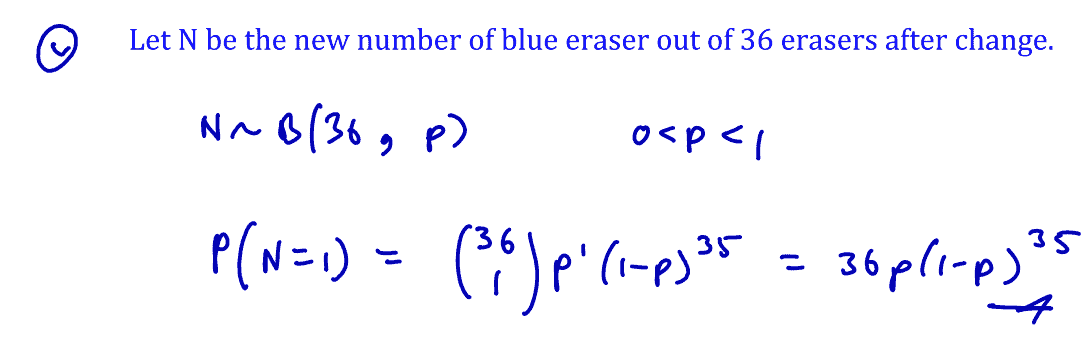
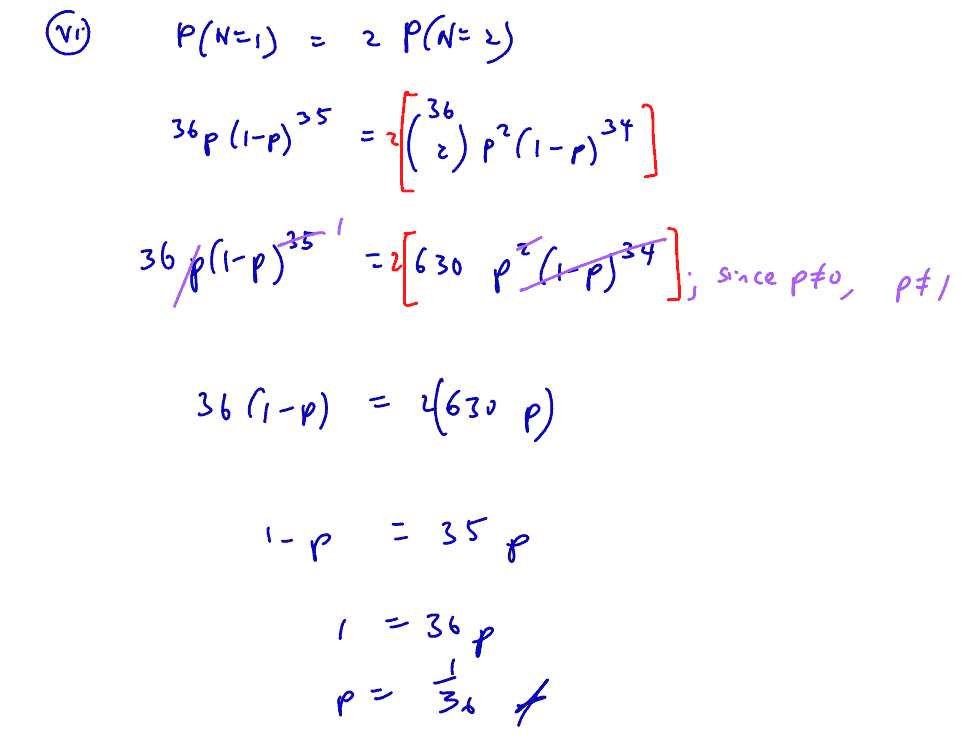
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
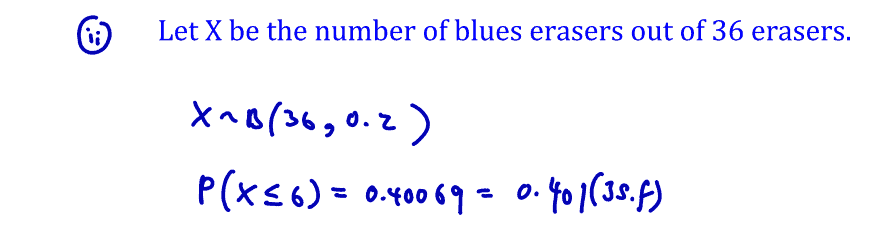


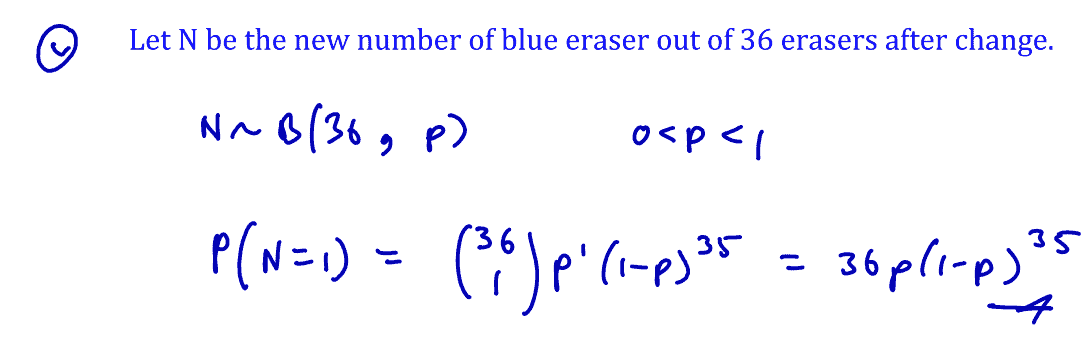
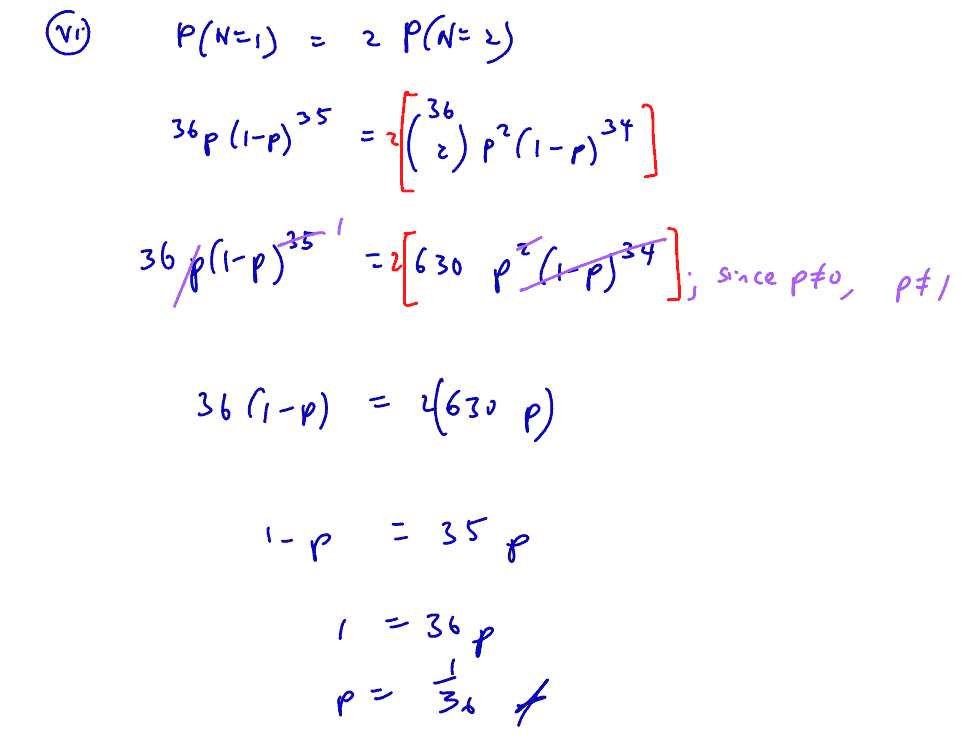
Share with your friends!
Download Binomial Distribution Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
