A-Level H2 Math | 5 Essential Questions
Complex Numbers
Complex numbers are numbers with a real part and an imaginary part, $\text{i}$. Complex numbers are generally written in the form $a+b\text{i}$ where the imaginary number $\text{i}$ is equal to $\sqrt{-1}$. Complex numbers are the name mathematicians give to the generalization of real numbers that allow us to take square roots of negative numbers. This allow us to solve certain equations that had no real solution.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each question. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2017 NYJC P1 Q3
Do not use a calculator in answering this question.
(i)
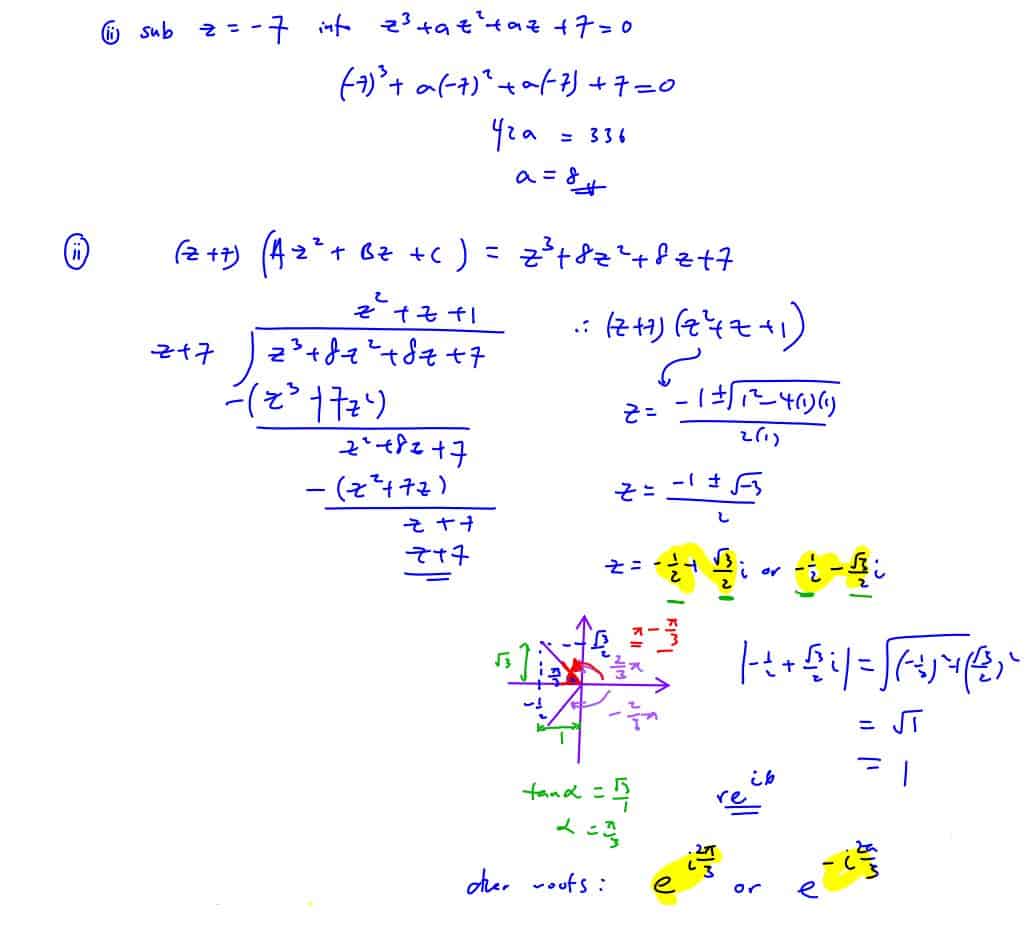
Explain why the equation ${{z}^{3}}+a{{z}^{2}}+az+7=0$ cannot have more than two non-real roots, where $a$ is a real constant.
[1]
(i) Explain why the equation ${{z}^{3}}+a{{z}^{2}}+az+7=0$ cannot have more than two non-real roots, where $a$ is a real constant.
[1]
(ii)
Given that $z=-7$ is a root of the equation in (i), find the other roots, leaving your answers in the form $r{{e}^{\text{i}\theta }}$, where $r>0$ and $-\pi <\theta \le \pi $ .
[4]
(ii) Given that $z=-7$ is a root of the equation in (i), find the other roots, leaving your answers in the form $r{{e}^{\text{i}\theta }}$, where $r>0$ and $-\pi <\theta \le \pi $ .
[4]
(iii)
Hence, solve the equation $\text{i}{{z}^{3}}+8{{z}^{2}}-8\text{i}z-7=0$, leaving your answers in the form $r{{e}^{\text{i}\theta }}$, where $r>0$ and $-\pi <\theta \le \pi $ .
[2]
(iii) Hence, solve the equation $\text{i}{{z}^{3}}+8{{z}^{2}}-8\text{i}z-7=0$, leaving your answers in the form $r{{e}^{\text{i}\theta }}$, where $r>0$ and $-\pi <\theta \le \pi $ .
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)


- (i)
- (ii)
- (iii)



Share with your friends!
2009 NJC P1 Q9 (b) Modified
Write down the real root of
${{w}^{3}}+8=0$,
Where $w$ is a complex number.
Hence, find the other roots of ${{w}^{3}}+8=0$ in exact form.
Deduce the roots of ${{w}^{4}}+{{w}^{3}}+8w+8=0$.
Determine the roots of $z$ such that ${{z}^{4}}-\mathbf{i}{{z}^{3}}+8\mathbf{i}z+8=0$.
Suggested Handwritten and Video Solutions

Share with your friends!
2014 JJC P1 Q10 (a)
Given that the complex number $z=(1+\text{i})t+\frac{1-\text{i}}{t}$ is represented by the point $P$ on Argand diagram where $t$ is a non-zero real constant. Find the Cartesian equation of the locus of the point $P$.
[3]
Suggested Handwritten and Video Solutions
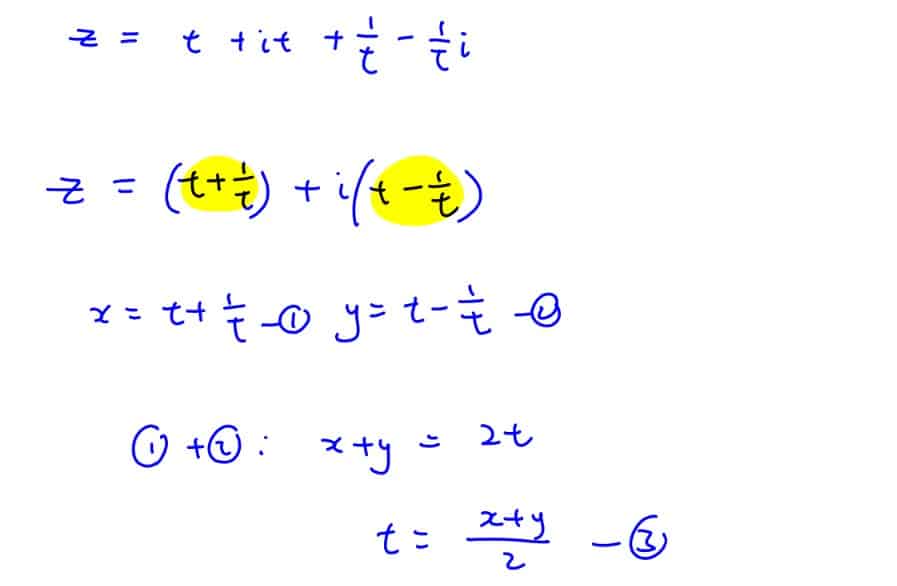
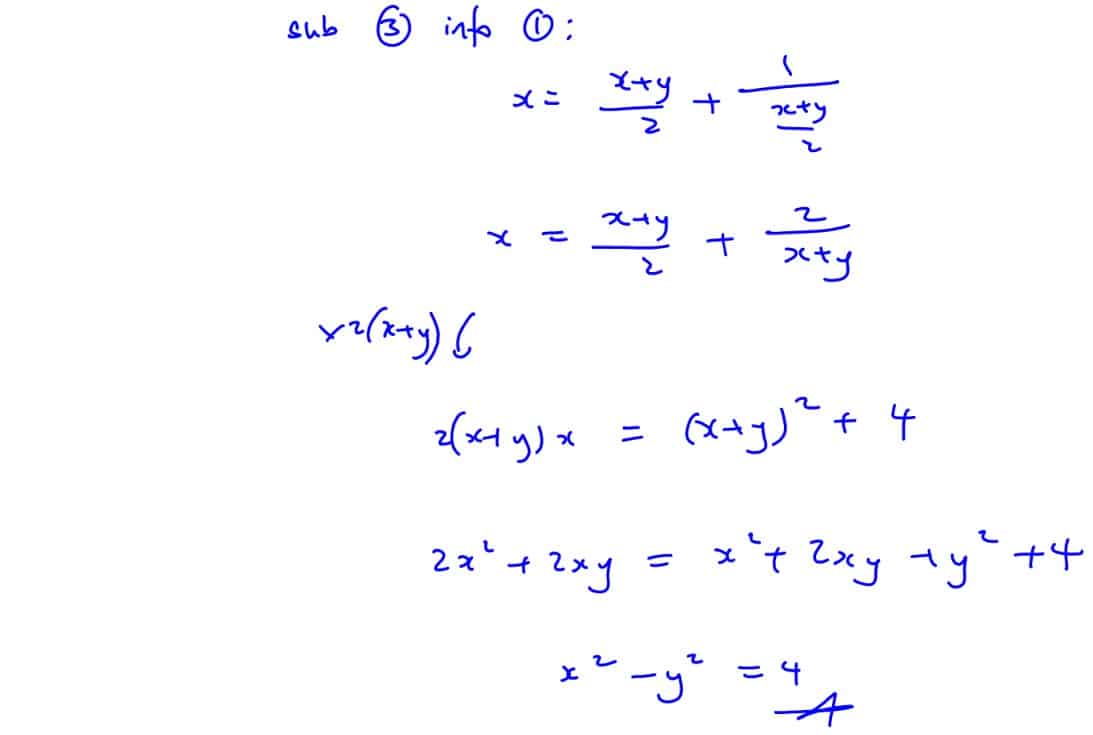
Share with your friends!
2020 CJC P1 Q2
The complex number $z$ has modulus $2$ and argument $\frac{\pi }{8}$ . It is also given that $w=1+\text{i}$.
(i)
Given that $n$ is an integer, find $\frac{{{z}^{n}}}{w*}$ in terms of $n$, giving your answer in the form $r{{e}^{i\theta }}$ .
[3]
(i) Given that $n$ is an integer, find $\frac{{{z}^{n}}}{w*}$ in terms of $n$, giving your answer in the form $r{{e}^{i\theta }}$ .
[3]
(ii)
Hence, find the smallest two positive integers $n$ such that $\frac{{{z}^{n}}}{w*}$ is real and negative.
[3]
(ii) Hence, find the smallest two positive integers $n$ such that $\frac{{{z}^{n}}}{w*}$ is real and negative.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
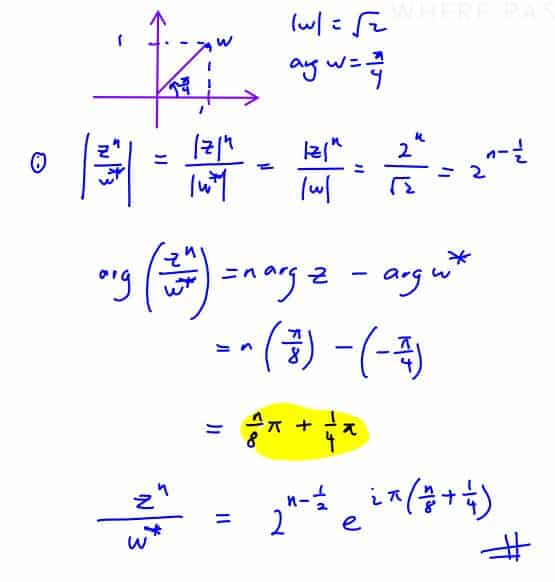

- (i)
- (ii)
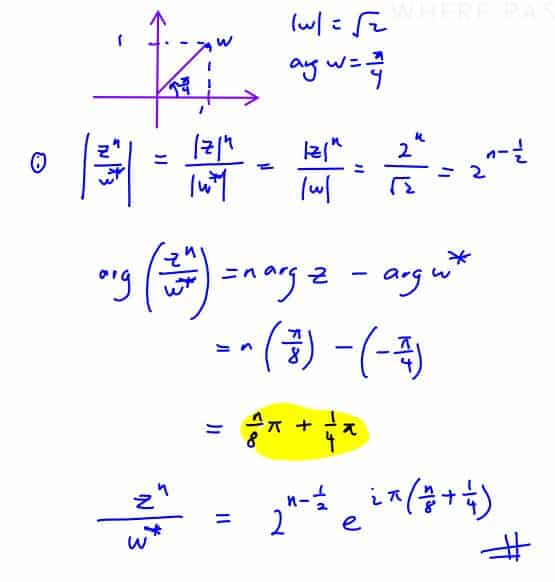

Share with your friends!
2015 RI P1 Q6 (b) Modified
Prove that $\frac{1+\sin \frac{3\pi }{8}+\text{i}\cos \frac{3\pi }{8}}{1+\sin \frac{3\pi }{8}-\text{i}\cos \frac{3\pi }{8}}=\cos \frac{\pi }{8}+\text{i}\sin \frac{\pi }{8}$.
Suggested Handwritten and Video Solutions
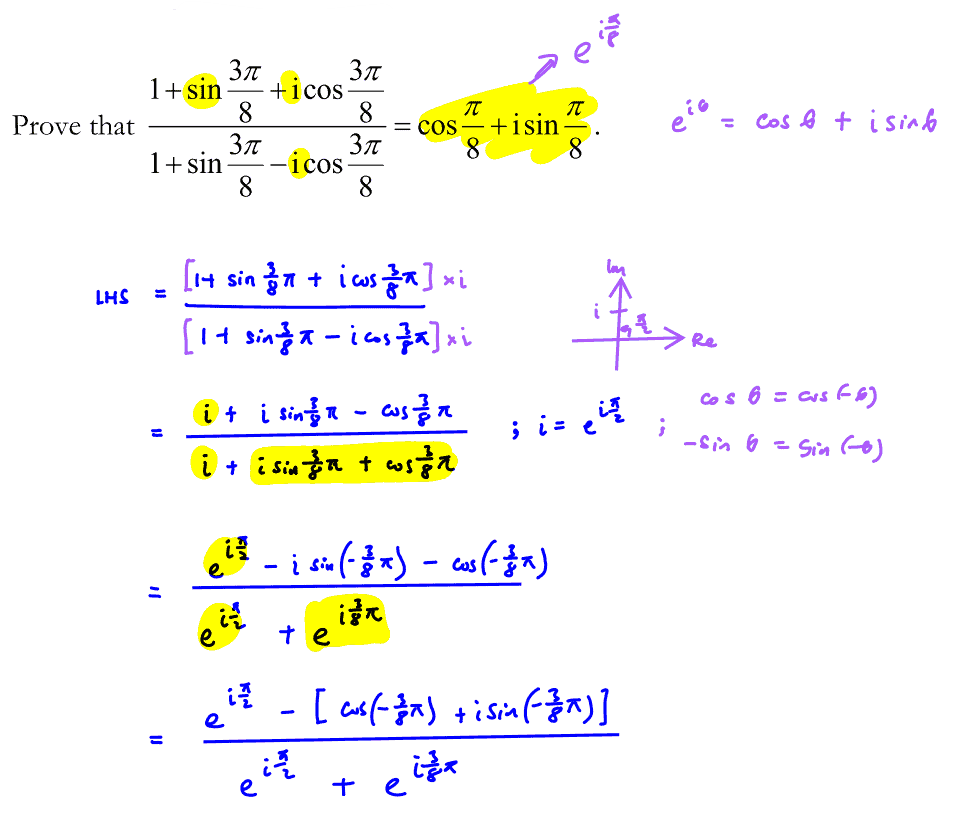
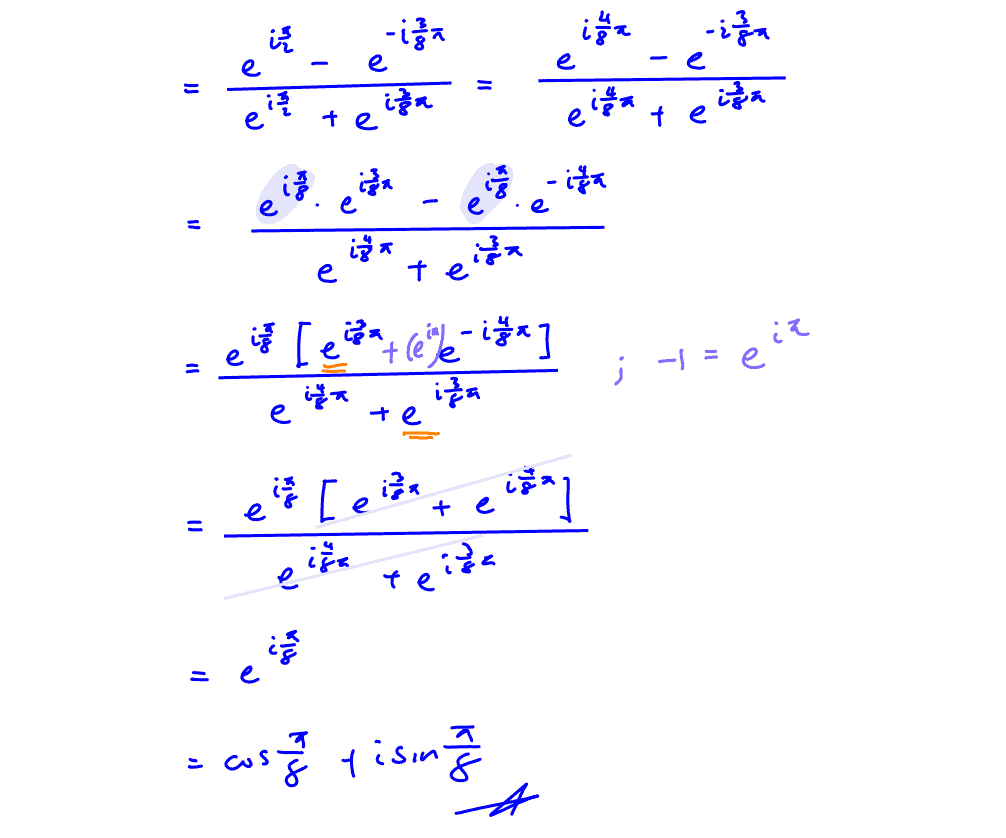
Share with your friends!
Download Complex Numbers Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
