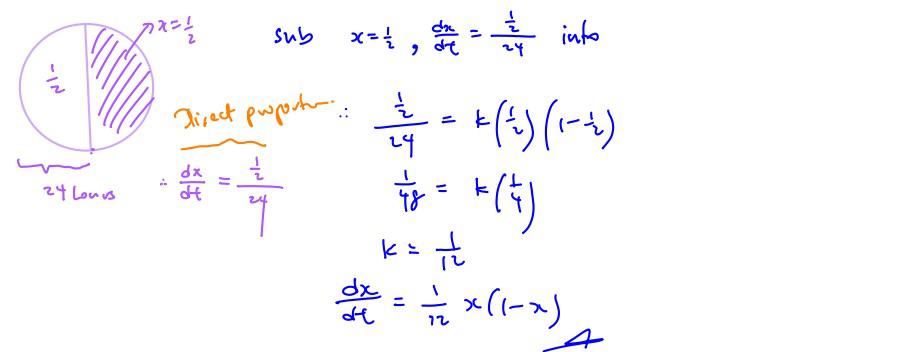A-Level H2 Math | 5 Essential Questions
Differential Equations
Differential equation refers to any equation that contains one or more functions and their derivatives. Differential equations are equations that describe how continuously changing quantities are related. They come in handy when modelling real-world phenomena that can be described by continuous change, such as population growth, falling objects, and mixing fluids.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each question. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2019 ACJC Promo Q3
Find the general solution of the differential equation $\frac{\text{d}m}{\text{d}v}=\frac{{{m}^{2}}+m+1}{m+1}$.
[5]
Suggested Handwritten and Video Solutions

Share with your friends!
2020 NYJC CT2 P1 Q10
The motion of a particle is described by the differential equation $\frac{{{\text{d}}^{2}}x}{\text{d}{{t}^{2}}}-4\frac{\text{d}x}{\text{d}t}+4x={{\text{e}}^{2t}}$, where $x$ is the displacement of the particle in metres along the $x$- axis with respect to origin $O$ at time $t$ seconds. By using the substitution $x=u{{\text{e}}^{2t}}$, show that this differential equation may be reduced to the form $\frac{{{\text{d}}^{2}}u}{\text{d}{{t}^{2}}}=a$, where $a$ is a constant to be determined.
Hence, find the displacement of the particle at time $t$ if the particle moves off from the initial point $x=1$ with a velocity of $1$m/s.
[7]
After some time, the particle is returned to its initial point and set into a new motion along the $x$- axis. The motion of the particle is described by the differential equation $\frac{\text{d}v}{\text{d}t}=2{{\text{e}}^{-v}}$, where $v$ is the velocity of the particle in metres per second at time $t$ seconds after it starts on this new motion. If the particle is at rest just before it begins this new motion, find an expression for $t$ in terms of $v$.
Show that $2x=3+{{\text{e}}^{v}}(v-1)$, where $x$ is the horizontal displacement of the particle in metres.
[6]
Suggested Handwritten and Video Solutions
- I
- II
- III
- IV
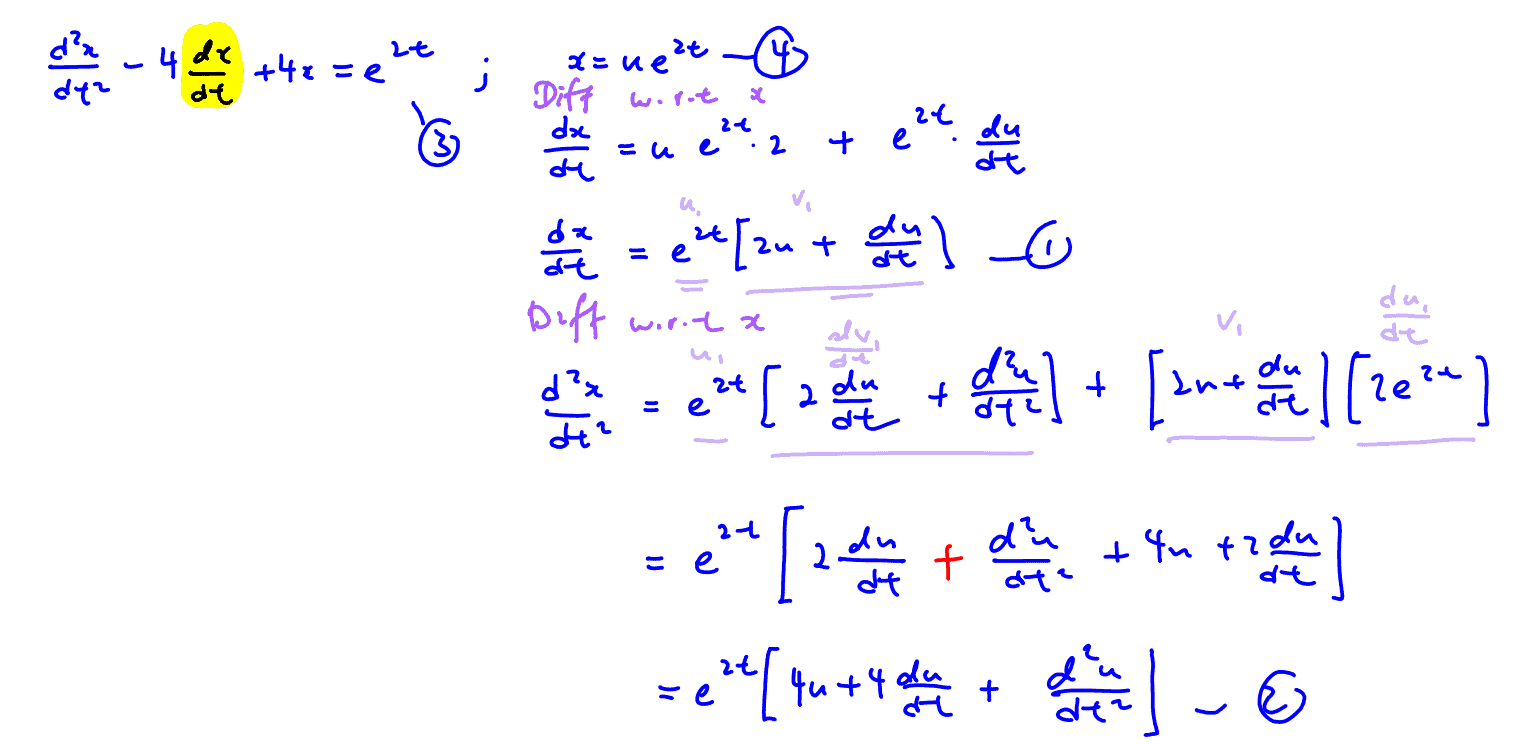
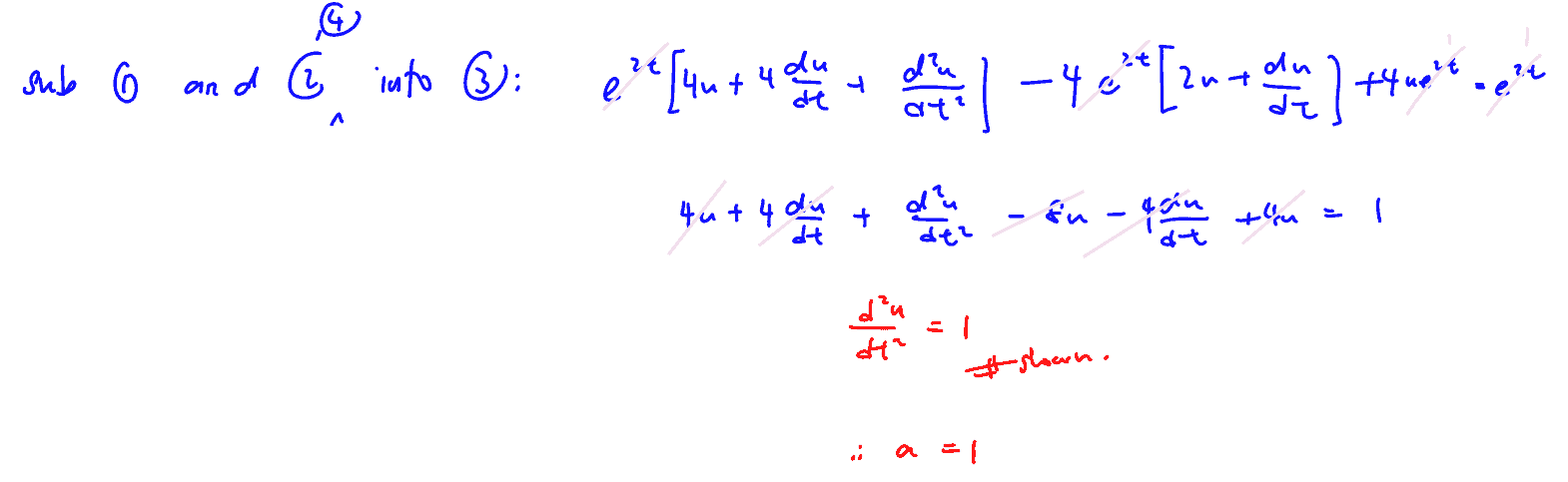
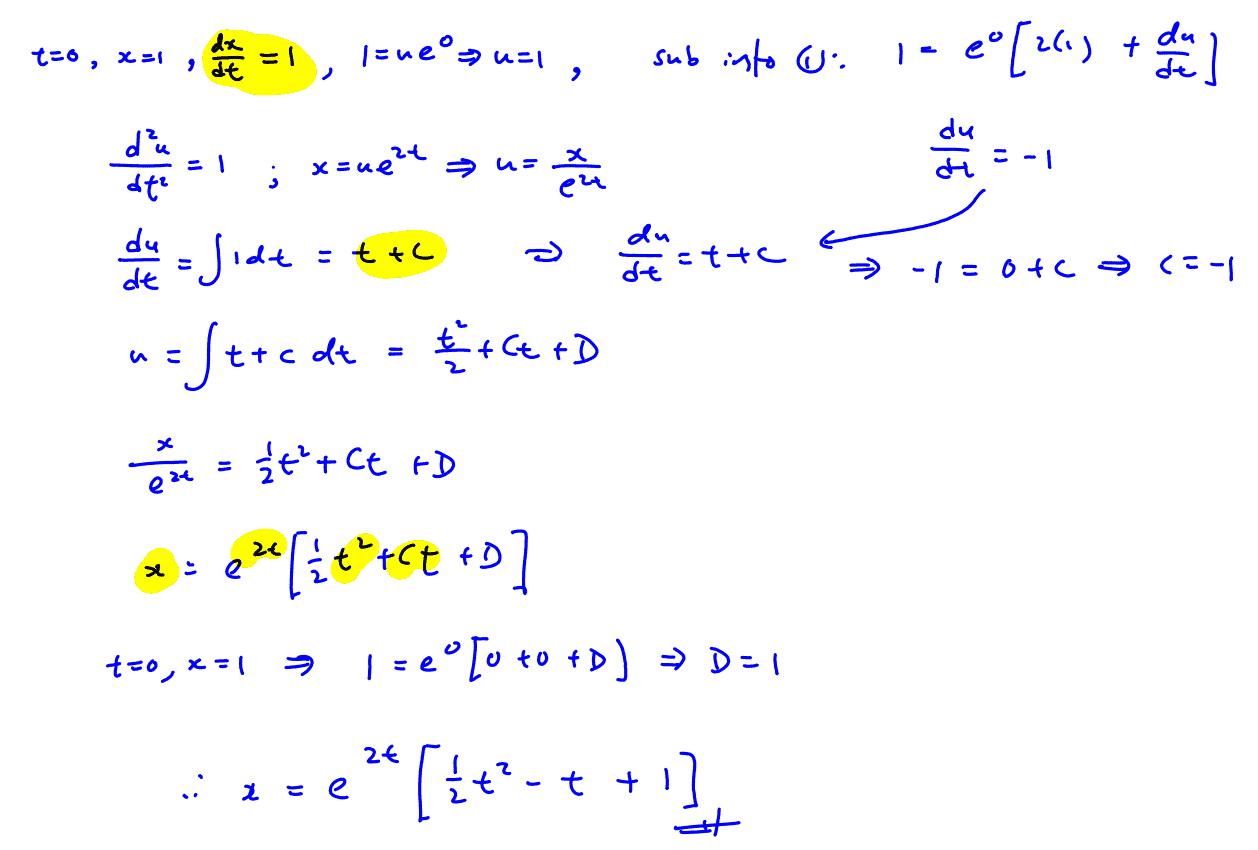
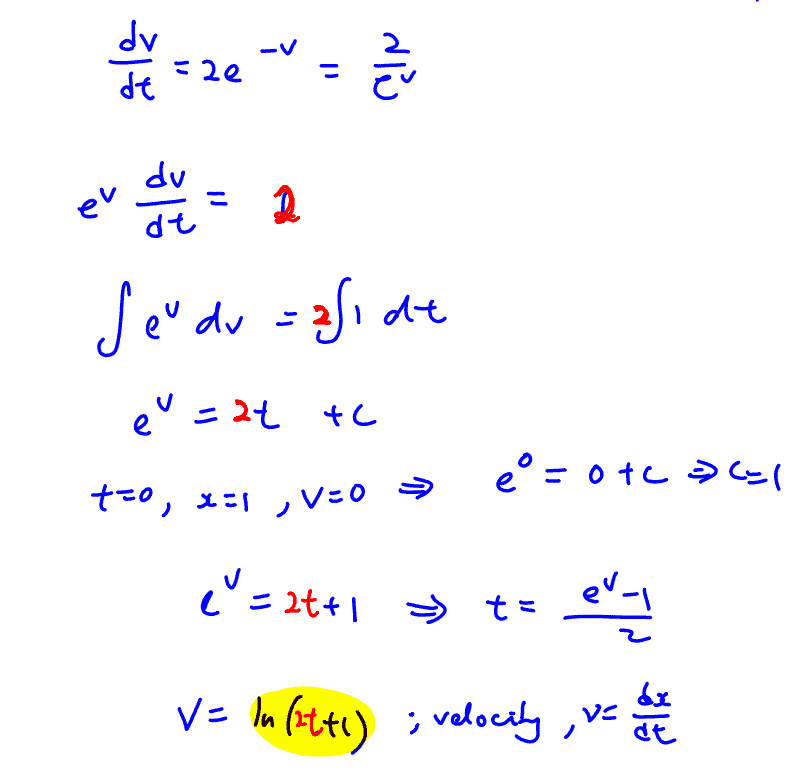
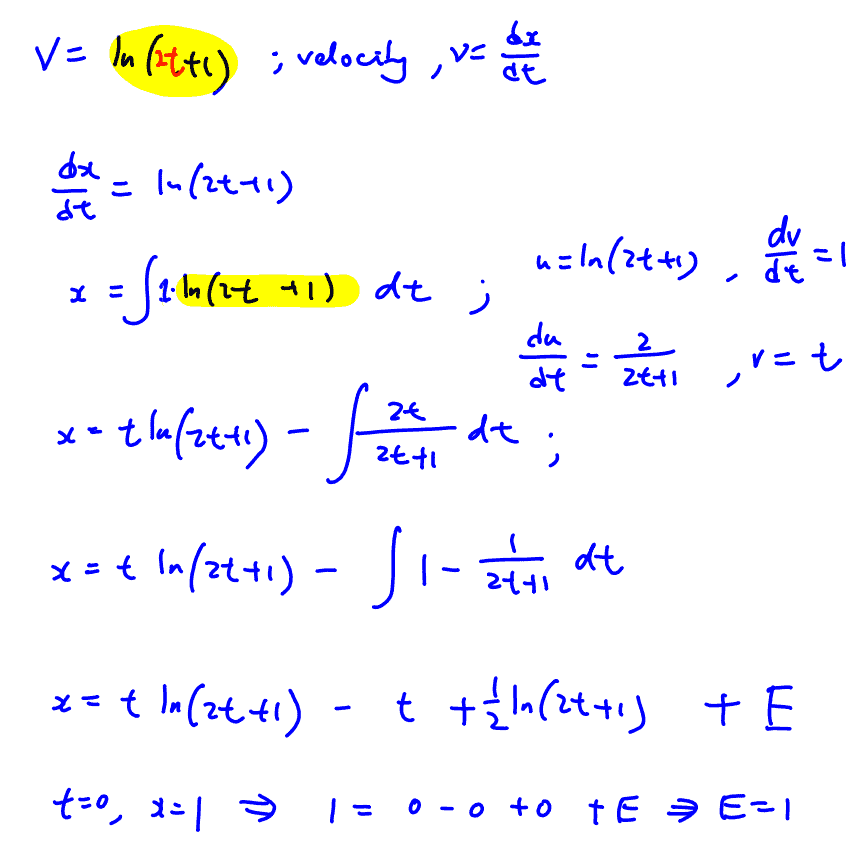
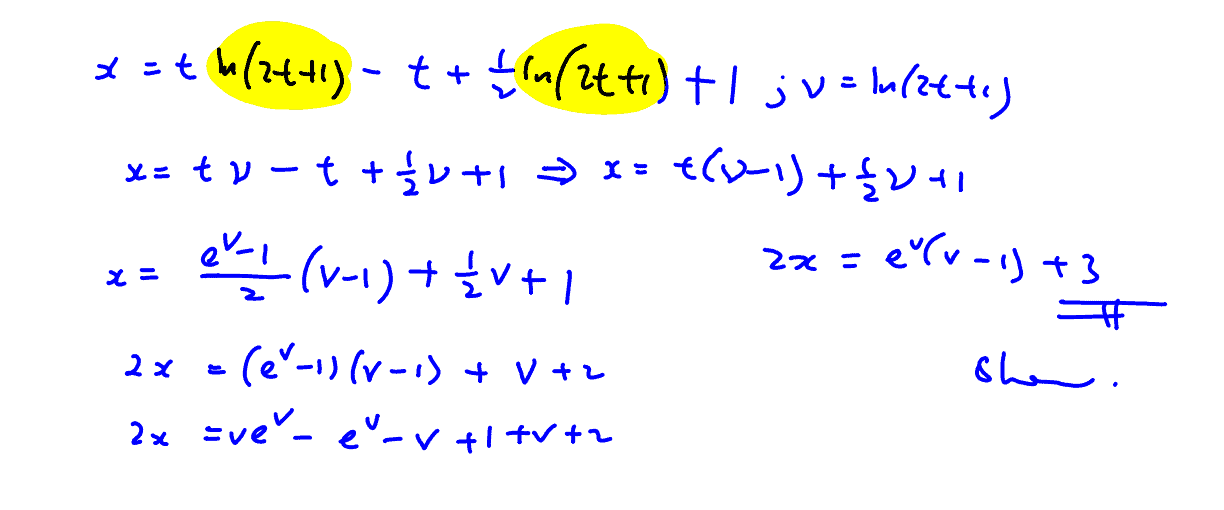
- I
- II
- III
- IV
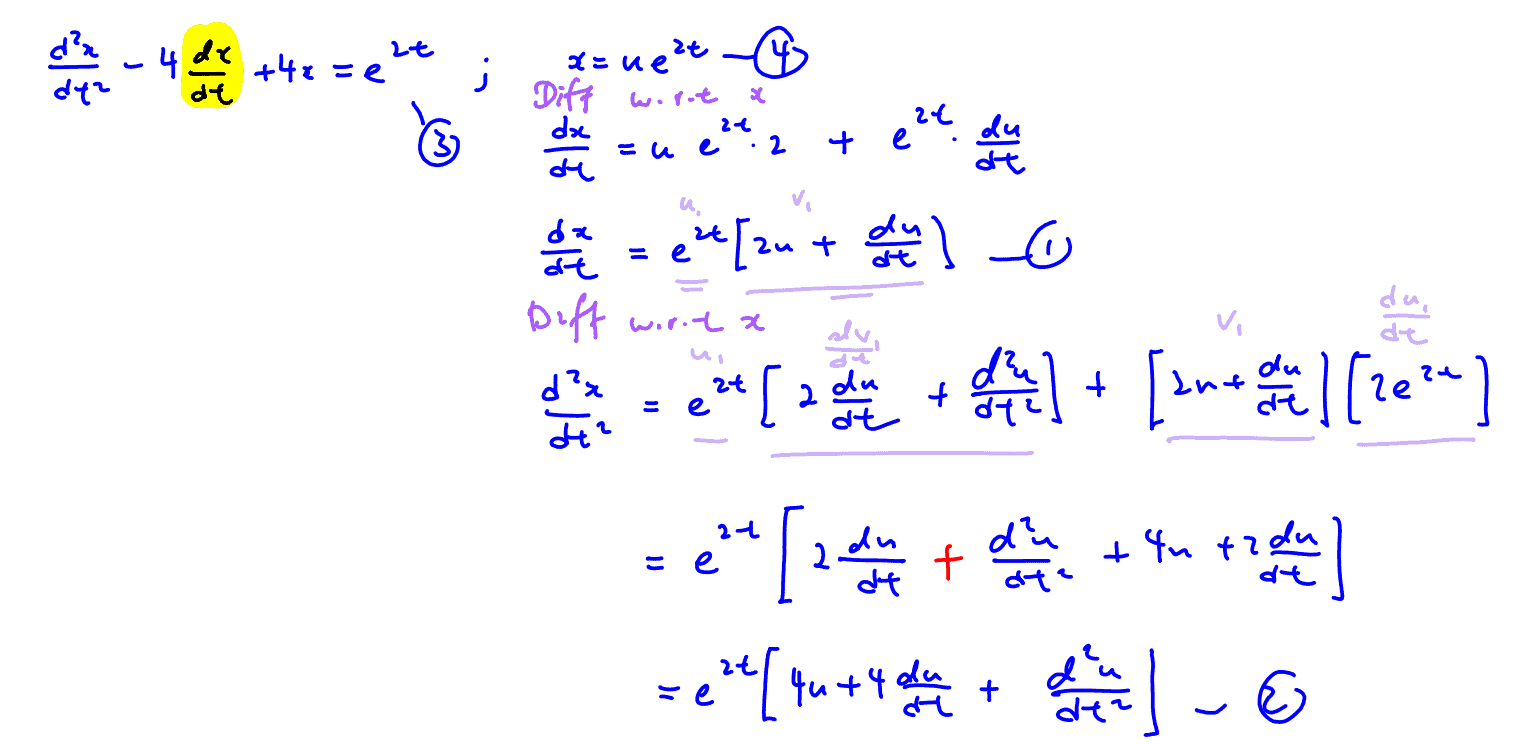
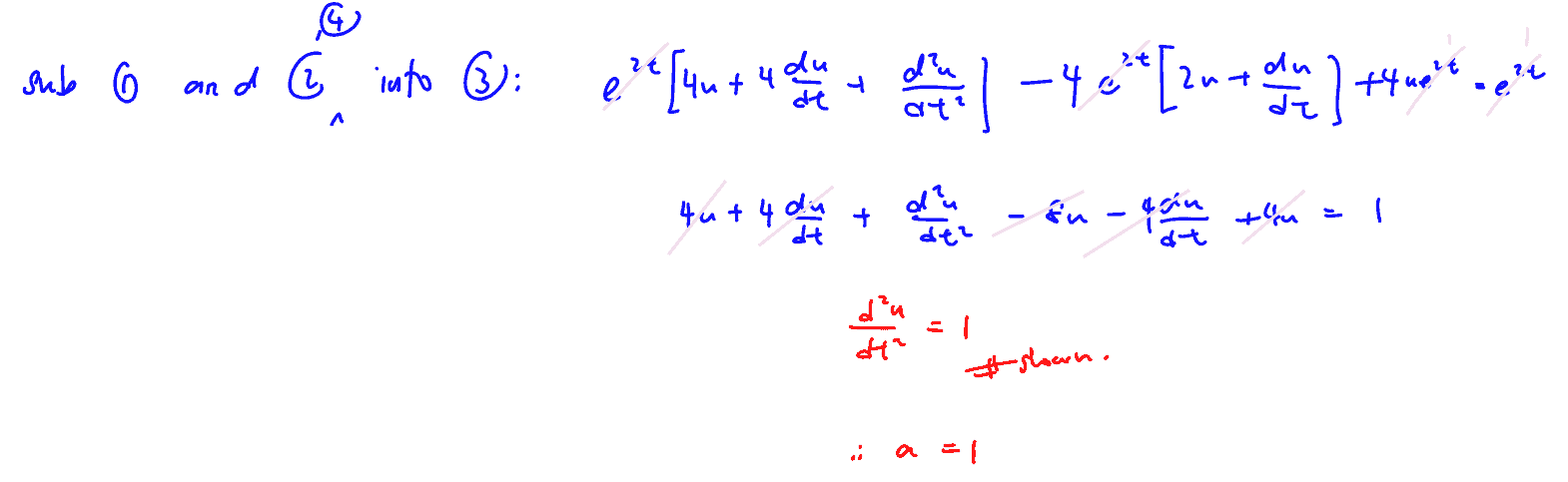
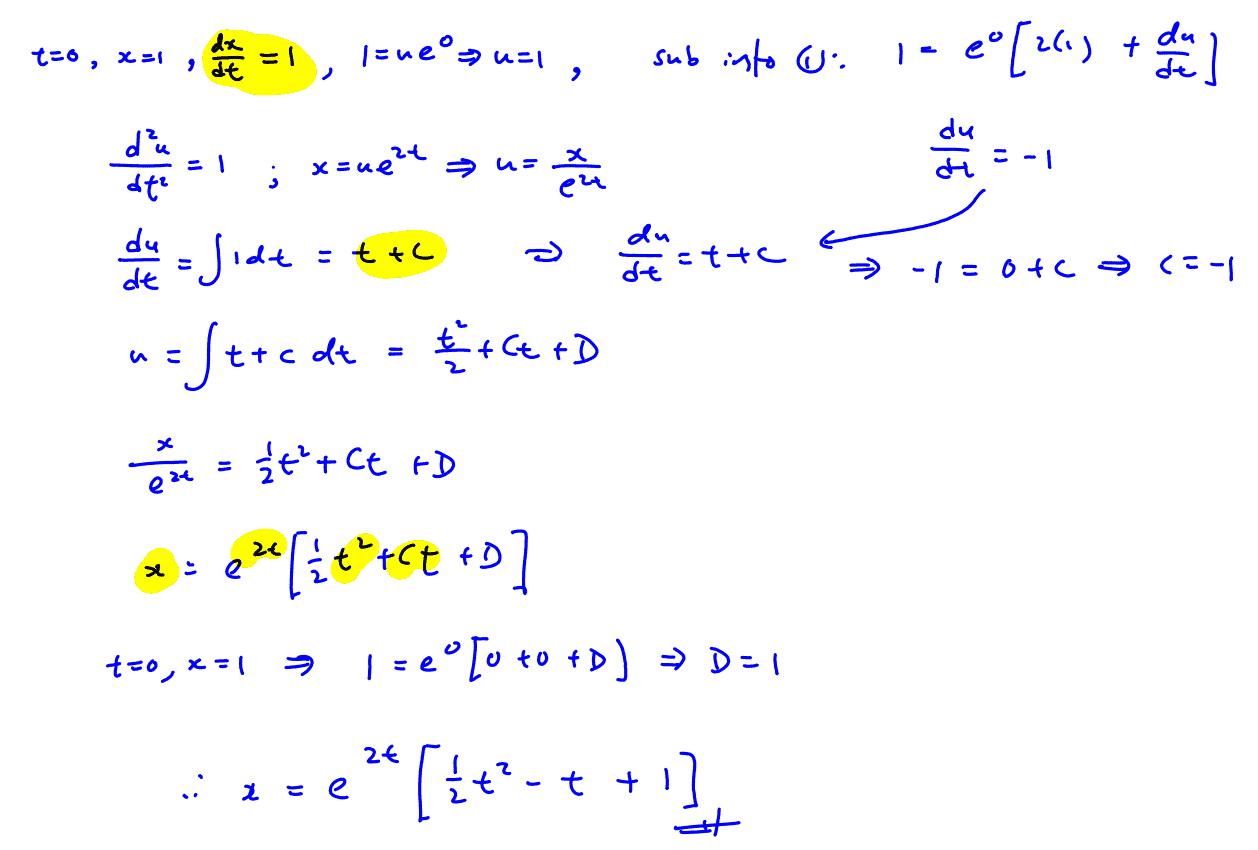
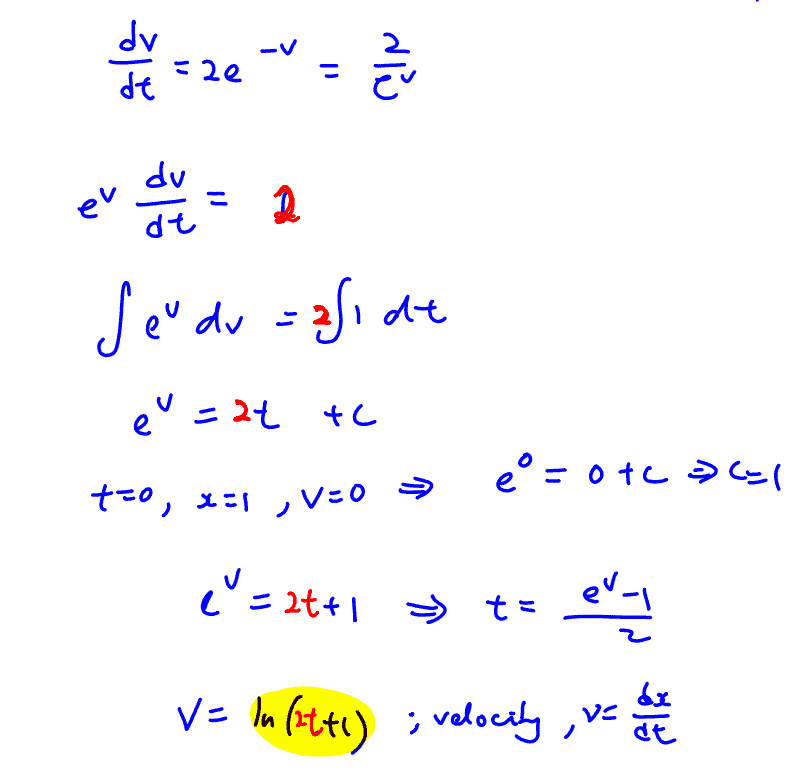
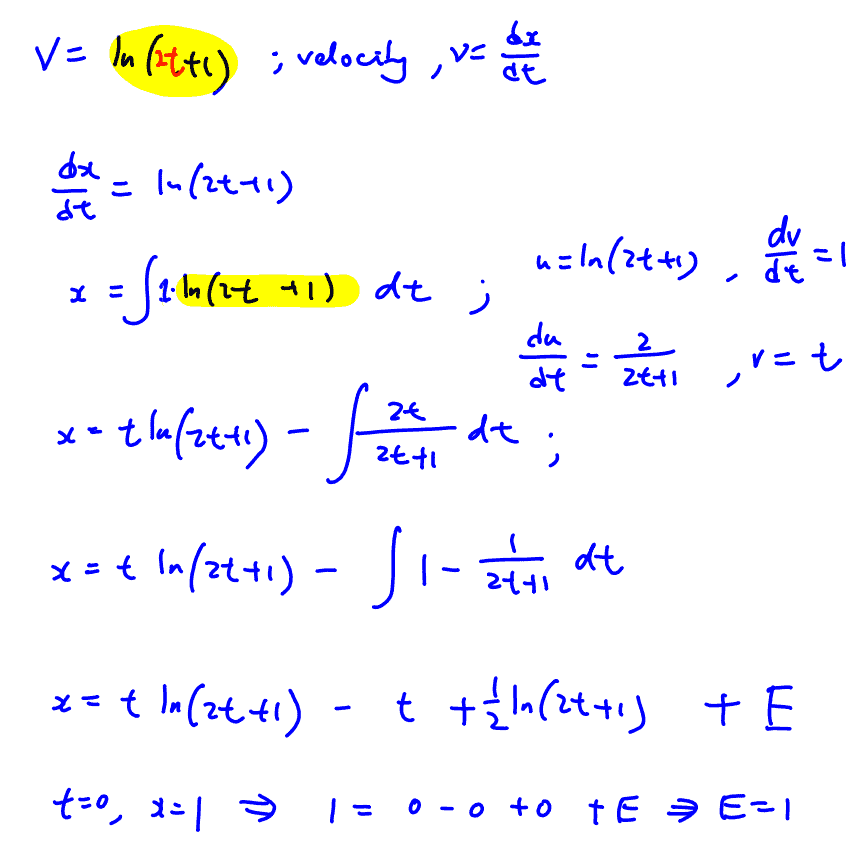
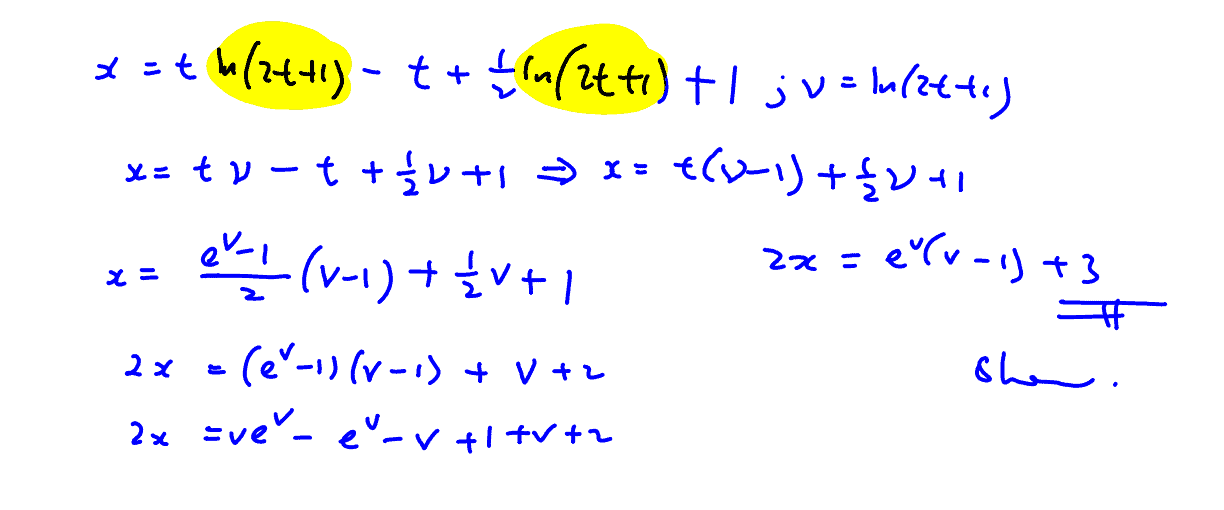
Share with your friends!
IJC P2 Q5 (b) Modified
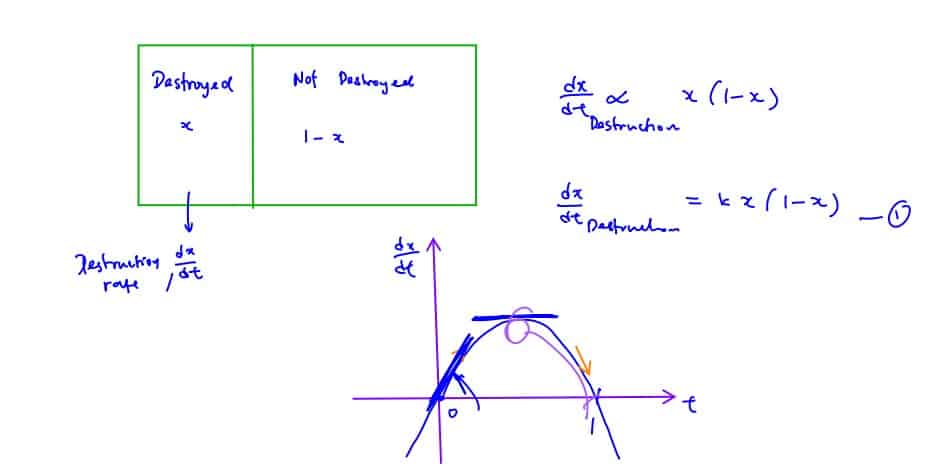
In established forest fires, the proportion of the total area of the forest which has been destroyed is denoted by $x$, and the rate of change of $x$ with respect to time, $t$ hours, is called the destruction rate. Investigations show that the destruction rate is directly proportional to the product of the proportion destroyed and the proportion not destroyed. A particular fire is initially noticed when one half of the forest is destroyed, and it is found that the destruction rate at this time is such that, if it remained constant thereafter, the forest would be destroyed completely in a further 24 hours.
Show that $12\frac{\text{d}x}{\text{d}t}=x(1-x)$ .
[3]
Deduce that approximately 73% of the forest is destroyed 12 hours after it is first noticed.
[6]
Suggested Handwritten and Video Solutions
Share with your friends!
2018 EJC JC2 MYE P2 Q4
A tank has a capacity of 100 litres. Initially, the tank contains 10 litres of water thoroughly mixed with 300 grams of salt. Salt water with a concentration of 5 g/litre is poured into the tank at a constant rate of 2 litres per minute, while the mixture flows out at a constant rate of 1 litre per minute.
Let $S$ denote the amount of dissolved salt in the tank (in grams) at time $t$ minutes after salt water is poured into the tank.
(i)
Show that $\frac{\text{d}S}{\text{d}t}=10-\frac{S}{t+10}$, stating your assumption(s) clearly.
[2]
(i) Show that $\frac{\text{d}S}{\text{d}t}=10-\frac{S}{t+10}$, stating your assumption(s) clearly.
[2]
(ii)
By substituting $Q=\left( t+10 \right)S$, solve the differential equation in (i), and find $S$ in terms of $t$.
[4]
(ii) By substituting $Q=\left( t+10 \right)S$, solve the differential equation in (i), and find $S$ in terms of $t$.
[4]
(iii)
Hence, find the concentration of salt in the tank at the point just before it overflows.
[2]
(iii) Hence, find the concentration of salt in the tank at the point just before it overflows.
[2]
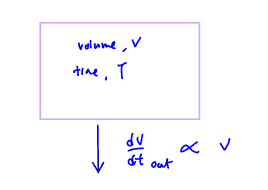
Once the volume of salt solution in the tank reaches 100 litres, the pouring stops, and the tank is allowed to drain off. The salt solution drains from the tank at a rate proportional to the volume of solution in the tank. Let $V$ denote the volume of solution in the tank at time $T$ after the tank starts to drain off.
(iv)
If the tanks takes 10 minutes to drain half of its contents, find $V$ in terms of $T$.
[4]
(iv) If the tanks takes 10 minutes to drain half of its contents, find $V$ in terms of $T$.
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
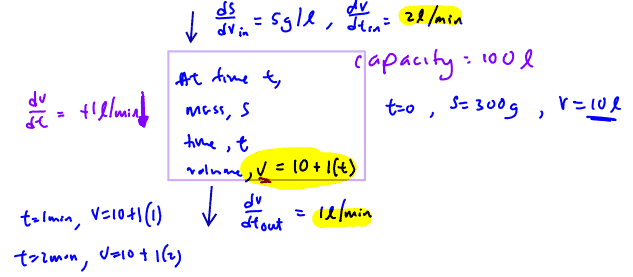
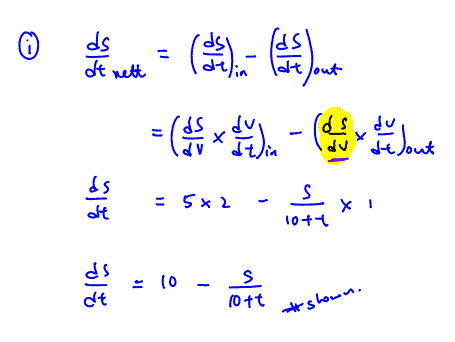
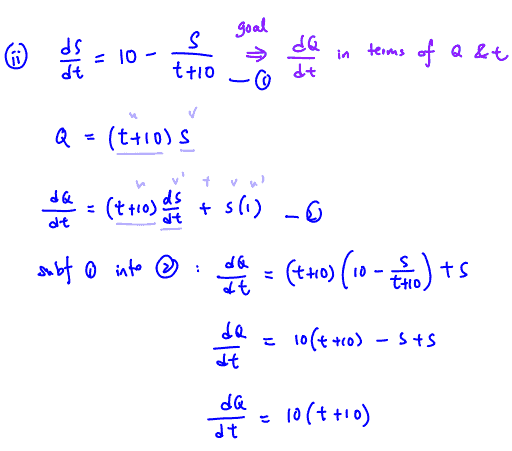
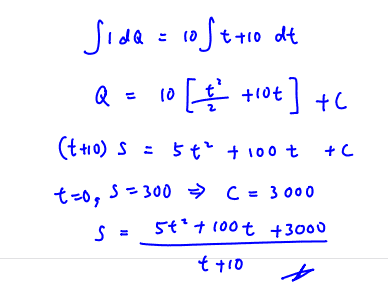
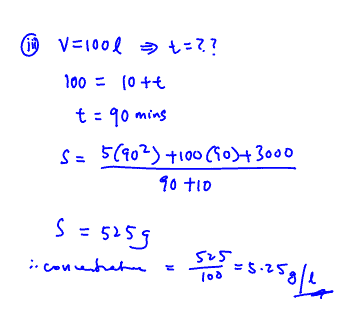

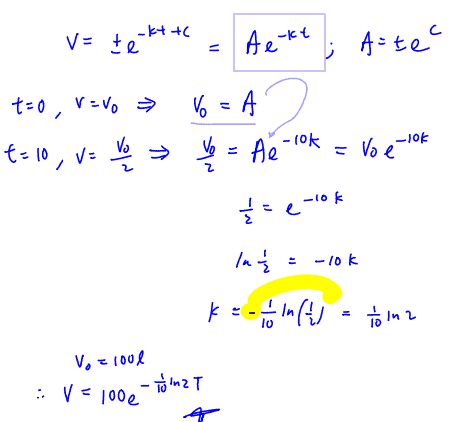
- (i)
- (ii)
- (iii)
- (iv)
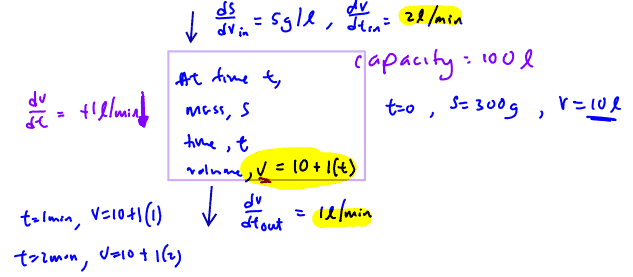
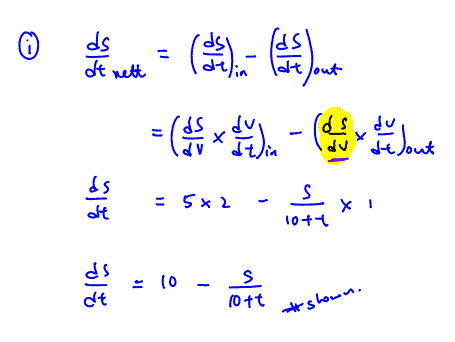
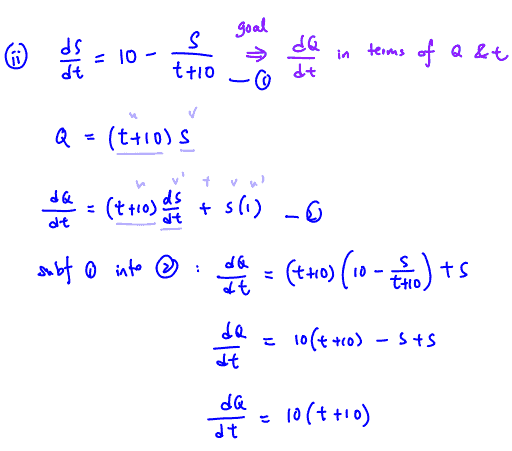
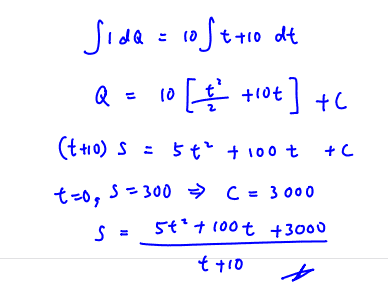
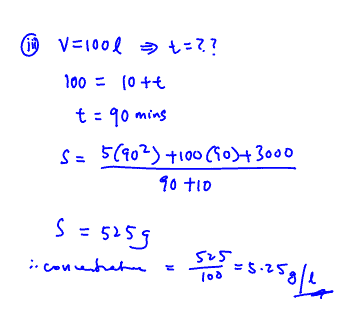


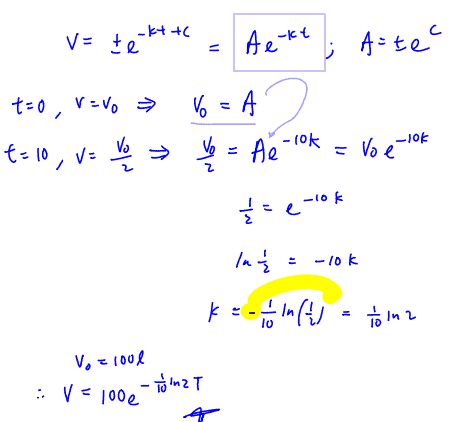
Share with your friends!
2019 NYJC P1 Q7
A spherical tank with negligible thickness and internal radius $a$cm contains water. At time $t$s, the water surface is at a height $x$cm above the lowest point of the tank and the volume of water in the tank, $V$cm$^{3}$, is given by $V=\frac{1}{3}\pi {{x}^{2}}\left( 3a-x \right)$. Water flows from the tank, through an outlet at its lowest point, at a rate $\pi k\sqrt{x}$cm$^{3}$ s$^{-1}$, where $k$ is a positive constant.
(i)
Show that $\left( 2ax-{{x}^{2}} \right)\frac{\text{d}x}{\text{d}t}=-k\sqrt{x}$.
[2]
(i) Show that $\left( 2ax-{{x}^{2}} \right)\frac{\text{d}x}{\text{d}t}=-k\sqrt{x}$.
[2]
(ii)
Find the general solution for $t$ in terms of $x$,$a$ and $k$.
[3]
(ii) Find the general solution for $t$ in terms of $x$,$a$ and $k$.
[3]
(iii)
Find the ratio ${{T}_{1}}:{{T}_{2}}$, where ${{T}_{1}}$ is the time taken to empty the tank when initially it is completely full, and ${{T}_{2}}$ is the time taken to empty the tank when initially it is half full.
[4]
(iii) Find the ratio ${{T}_{1}}:{{T}_{2}}$, where ${{T}_{1}}$ is the time taken to empty the tank when initially it is completely full, and ${{T}_{2}}$ is the time taken to empty the tank when initially it is half full.
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)

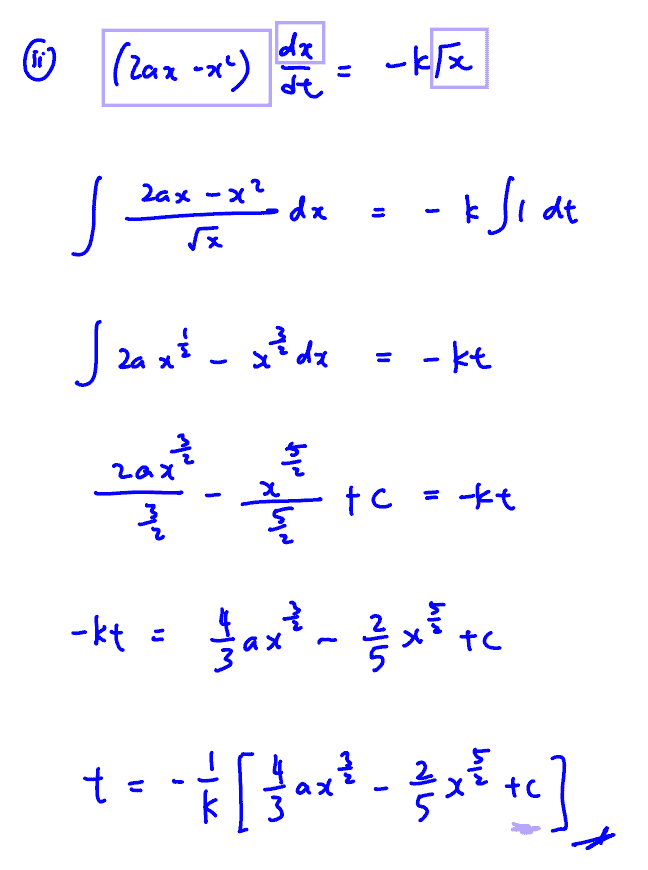
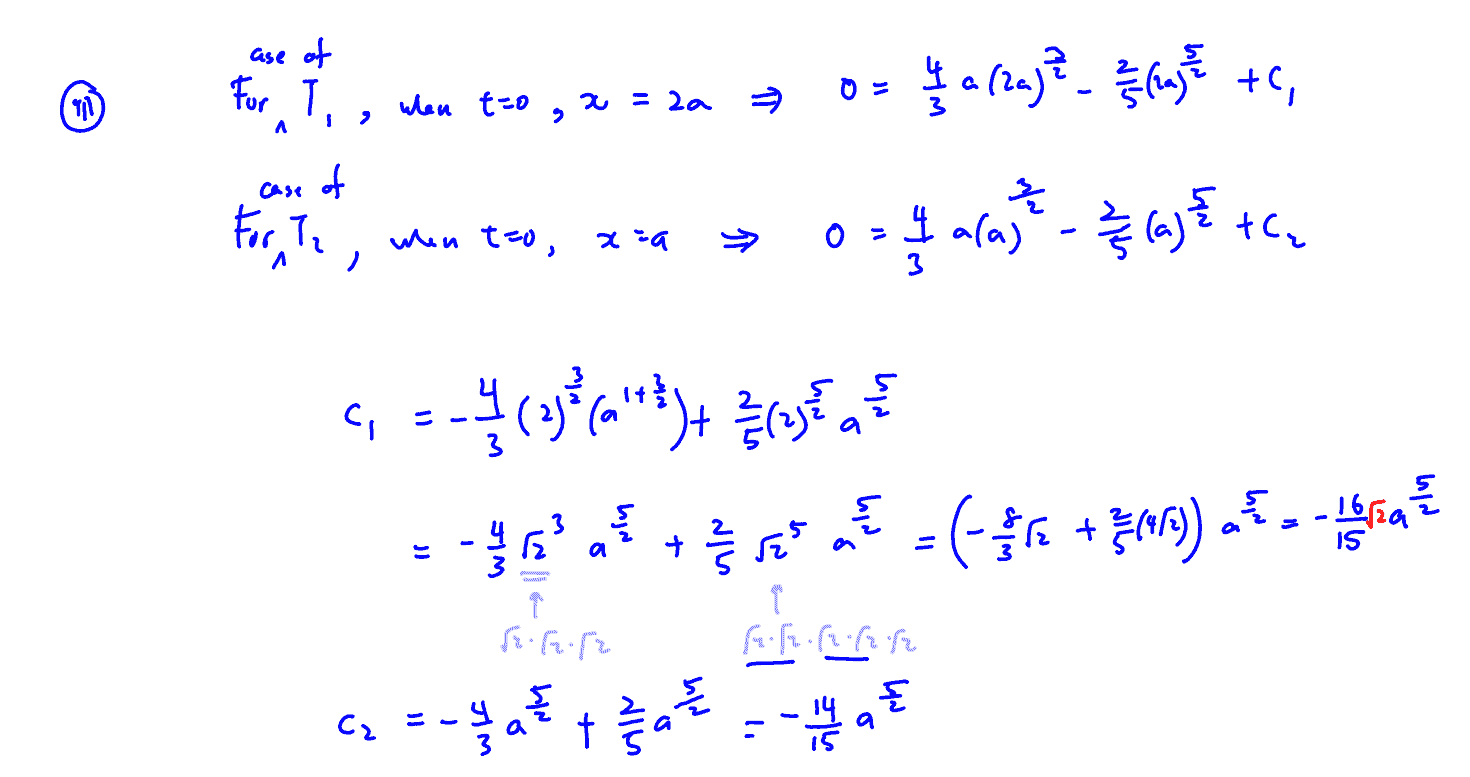
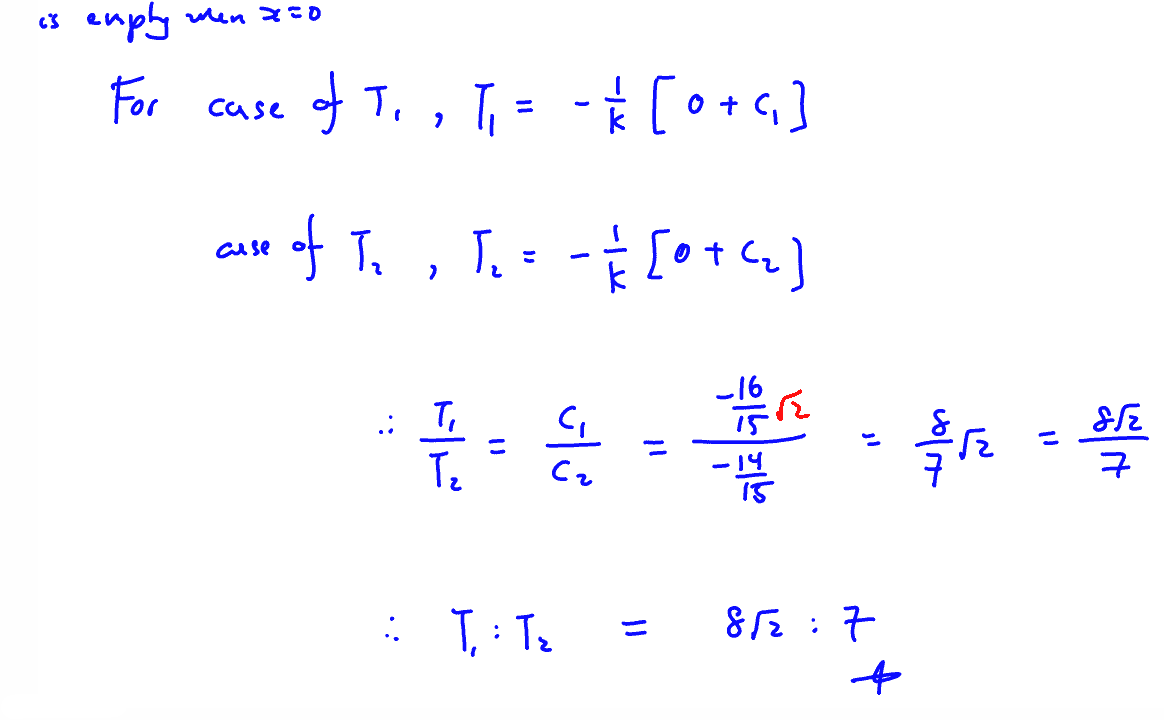
- (i)
- (ii)
- (iii)

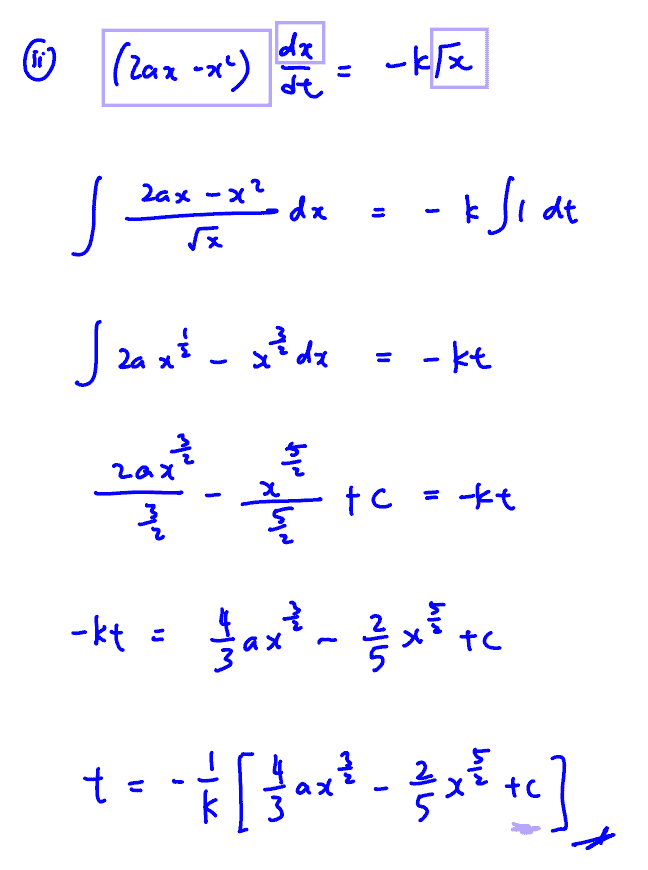
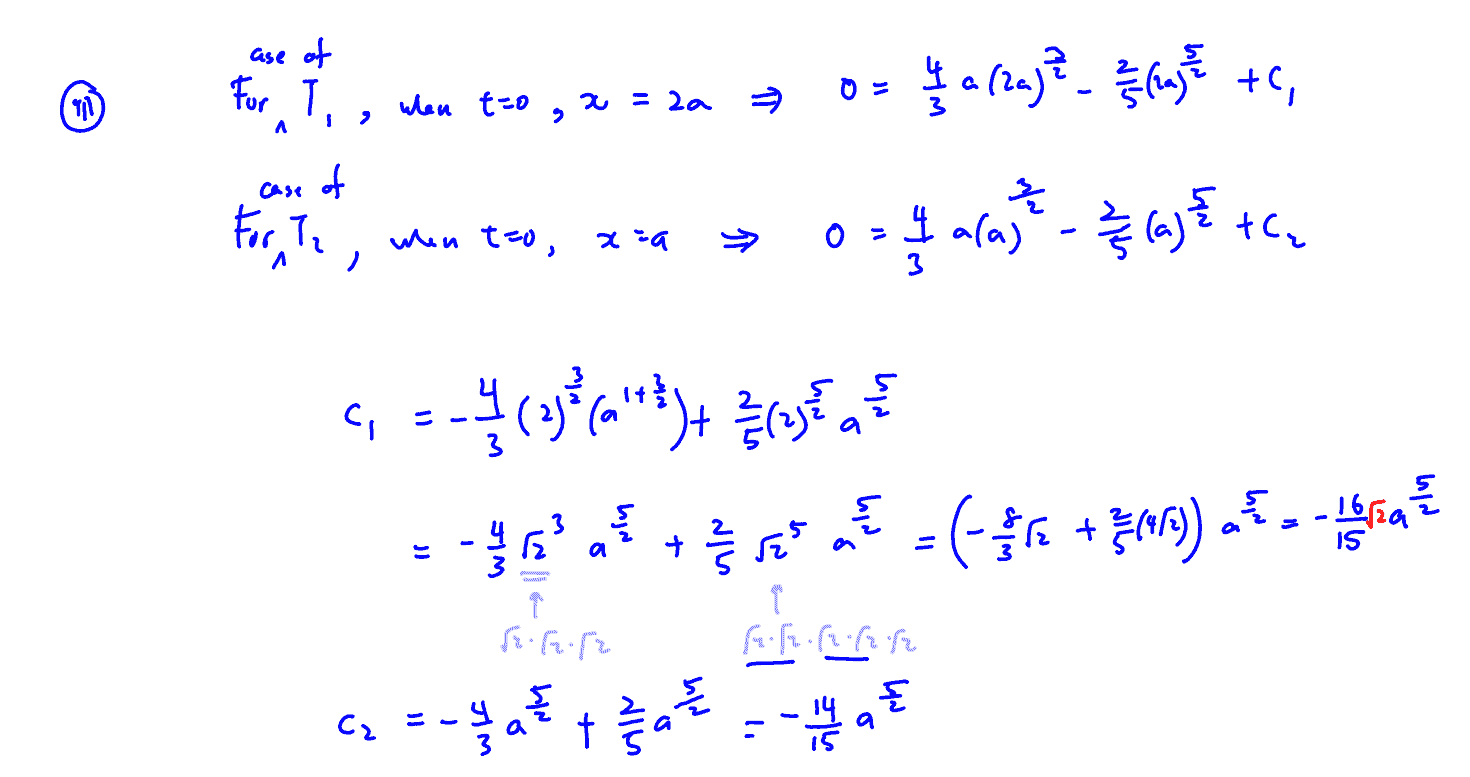
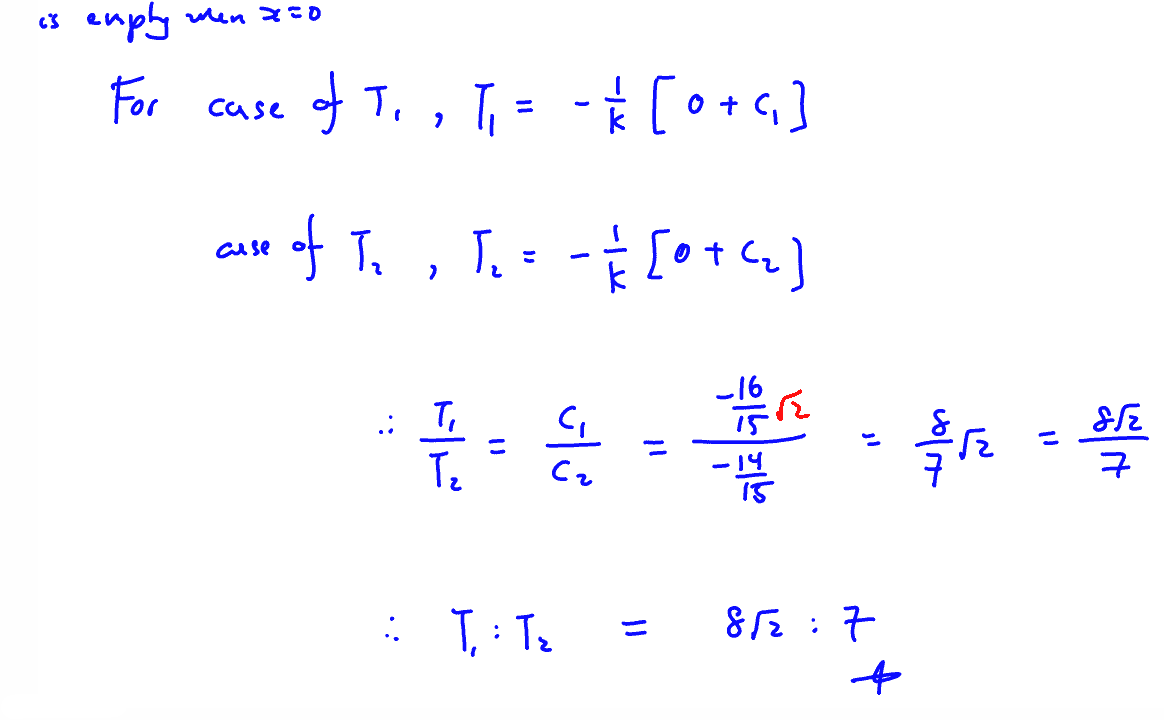
Share with your friends!
Download Differential Equations Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!