A-Level H2 Math | 5 Essential Questions
Discrete Random Variable
A discrete random variable can only take on either a finite or at most a countably infinite set of discrete values such as $0, 1, 2, 3, …$. Discrete random variables are often used to model the number of times an event occurs in a given time period. The sum of all the probabilities of the experiment is equal to $1$.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
These Ten-Year-Series (TYS) worked solutions with video explanations for 1977 A Level H2 Mathematics Paper 1 Question 12 are suggested by Mr Gan. For any comments or suggestions please contact us at support@timganmath.edu.sg.
N1977 P1 Q12
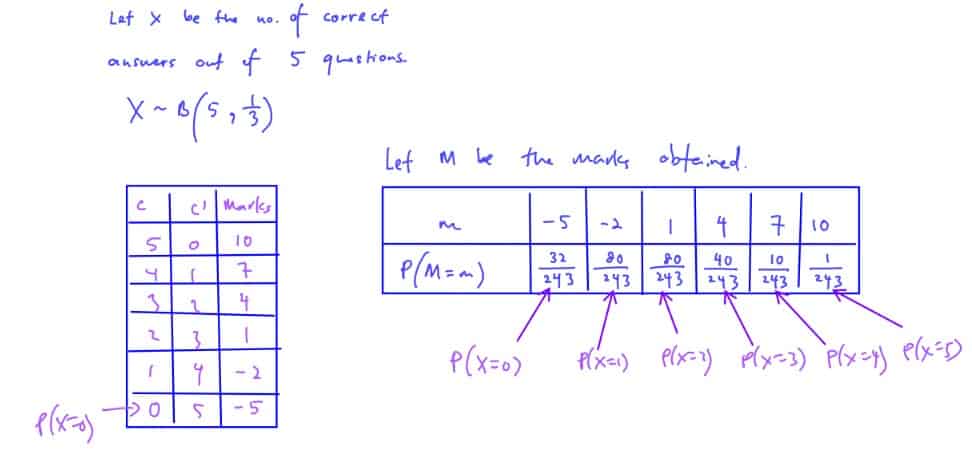
A test consists of five multiple choice questions to each of which three answers are given, only one of which is correct. For each correct answer a candidate gets $2$ marks, but loses $1$ mark for each incorrect answer. A particular candidate answers all question purely by guesswork. Draw up a table to show all the possible total marks from $-5$ to $10$ and the probability associated with each mark for this candidate. Use the table to show that the expected mark is zero, and find the variance of this distribution.
Suggested Handwritten and Video Solutions
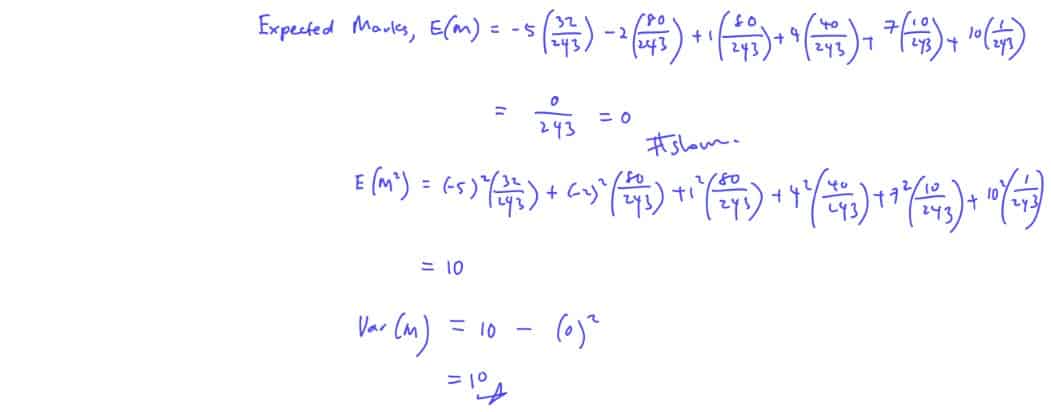
Share with your friends!
These Ten-Year-Series (TYS) worked solutions with video explanations for 1978 A Level H2 Mathematics Paper 2 Question 12 are suggested by Mr Gan. For any comments or suggestions please contact us at support@timganmath.edu.sg.
N1978 P2 Q12
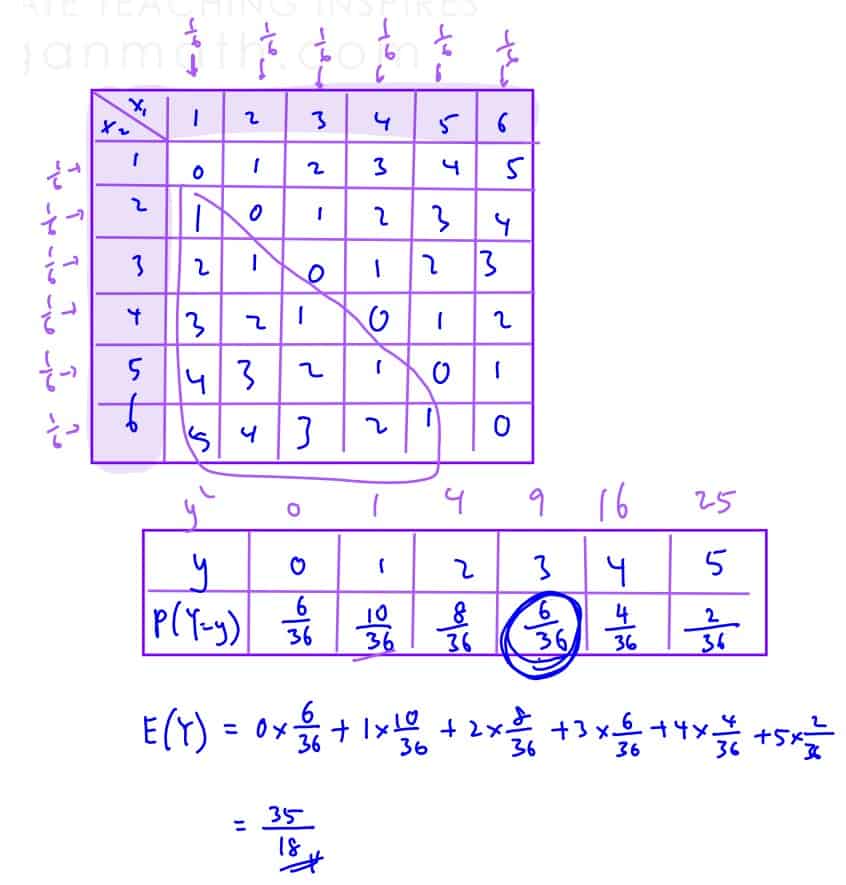
A fair die is thrown once and random variable $X$ denotes the score obtained. Write down $\text{E}\left( X \right)$ and show that $\text{Var}\left( X \right)=\frac{35}{12}$. The die is thrown twice, and ${{X}_{1}}$and${{X}_{2}}$ obtained from each attempt.
Tabulate the probability distribution of $Y=\left| {{X}_{1}}-{{X}_{2}} \right|$, and find $E\left( Y \right)$.
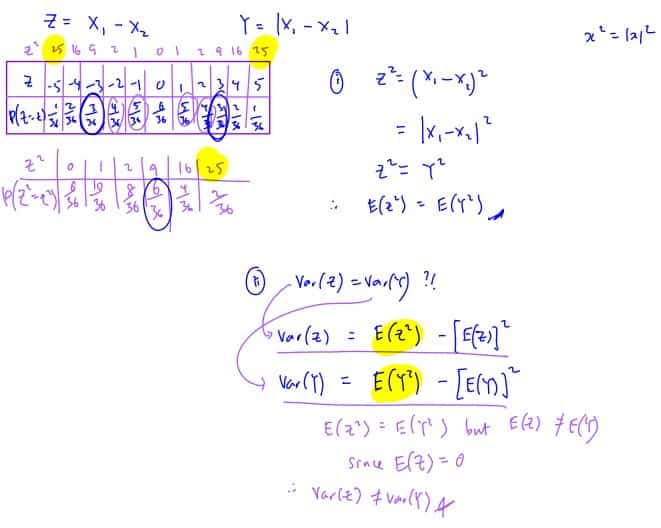
The random variable $Z$ is defined by $Z={{X}_{1}}-{{X}_{2}}$. State with reasons whether or not
(i)
$E\left( {{Z}^{2}} \right)=E\left( {{Y}^{2}} \right)$.
(ii)
$\text{Var}\left( Z \right)=\text{Var}\left( Y \right)$.
Suggested Handwritten and Video Solutions
- I
- II
- III

- I
- II
- III



Share with your friends!
2018 DHS P2 Q10
The discrete random variable $X$ has probability mass function given by
$\text{P}(X=x)=\left\{ \begin{matrix}
& \frac{ax}{n(n+1)}\,\,\,\,\text{for}\,\,x=1,2,…,n, \\
& 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{otherwise,} \\
\end{matrix} \right.$
where $a$ is a constant.
(i)
Show that $a=2$.
[2]
(i) Show that $a=2$.
[2]
(ii)
Find $\text{E}(X)$ in terms of $n$. You may use the result that $\sum\limits_{r=1}^{n}{{{r}^{2}}=\frac{n}{6}(n+1)(2n+1)}$.
[3]
(ii) Find $\text{E}(X)$ in terms of $n$. You may use the result that $\sum\limits_{r=1}^{n}{{{r}^{2}}=\frac{n}{6}(n+1)(2n+1)}$.
[3]
Two players ${{P}_{1}}$ and ${{P}_{2}}$ play a game with $n+1$ tokens labelled $1$ to $n+1$. Each player randomly picks one token without replacement and the player who picks the token with the smaller number loses. The amount of money lost by the losing player, in dollars, will be the number on the winning token. For example, if ${{P}_{1}}$ and ${{P}_{2}}$ pick the tokens labelled $5$ and $3$ respectively, ${{P}_{2}}$ loses $\$\,5$ to ${{P}_{1}}$.
(iii)
Explain why the probability of ${{P}_{2}}$ losing a game is $0.5$.
[1]
(iii) Explain why the probability of ${{P}_{2}}$ losing a game is $0.5$.
[1]
(iv)
Given that ${{P}_{2}}$ loses, find the probability ${{P}_{2}}$ loses $\$\,(m+1)$ in terms of $m$ and $n$, where $m$ is such that $1\le m\le n$.
[3]
(iv) Given that ${{P}_{2}}$ loses, find the probability ${{P}_{2}}$ loses $\$\,(m+1)$ in terms of $m$ and $n$, where $m$ is such that $1\le m\le n$.
[3]
(v)
Using the result in part (i), when ${{P}_{2}}$ loses a game, find the amount that he is expected to lose in terms of $n$.
[3]
(v) Using the result in part (i), when ${{P}_{2}}$ loses a game, find the amount that he is expected to lose in terms of $n$.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
- (v)
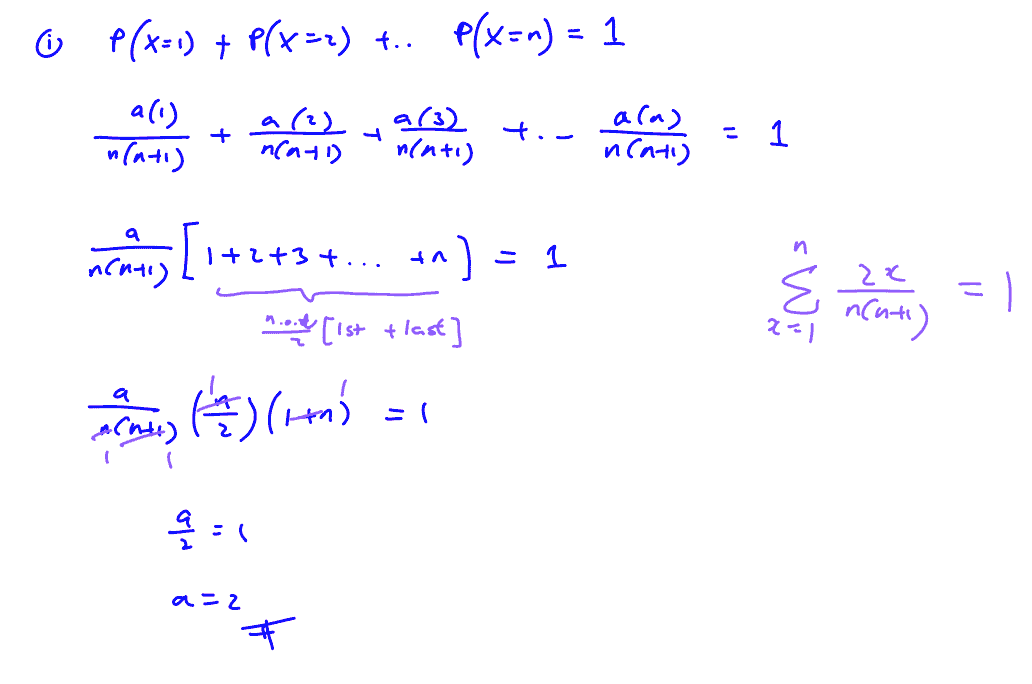
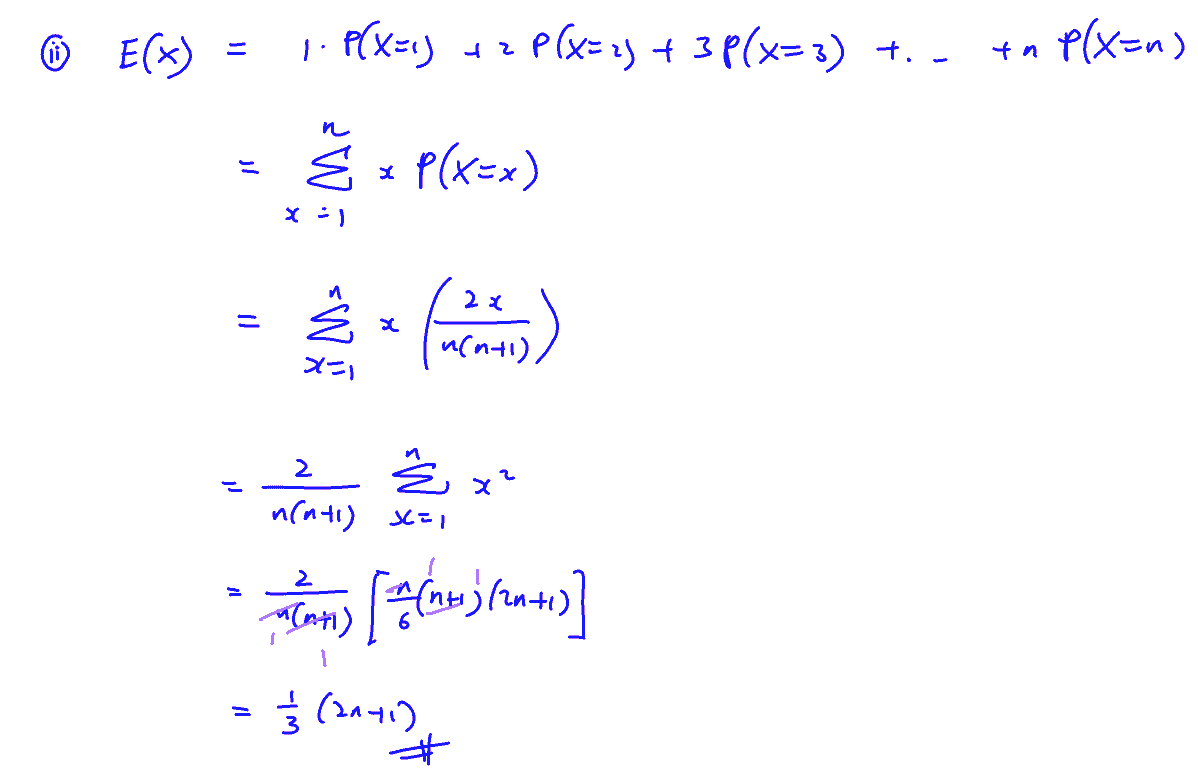
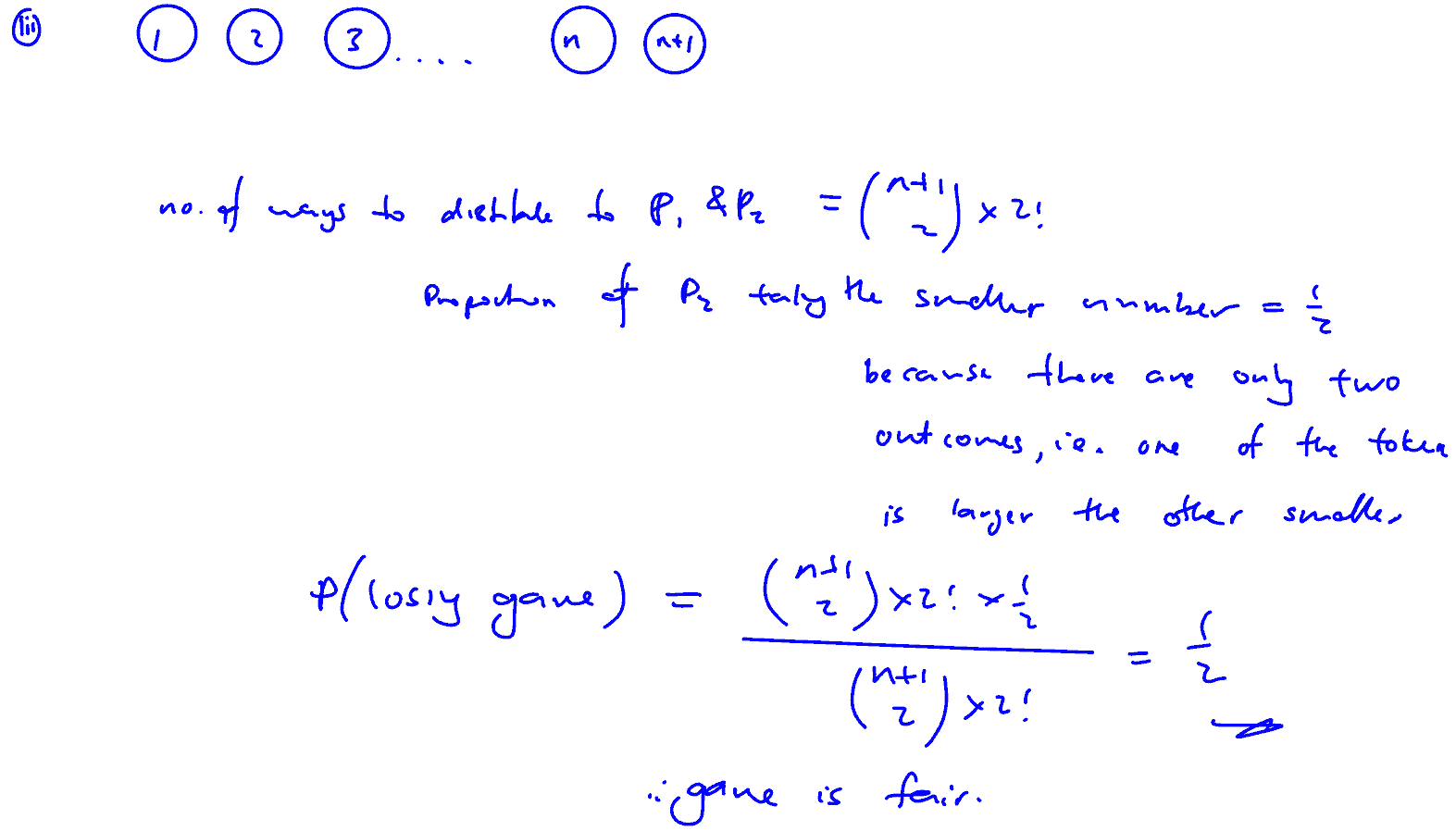
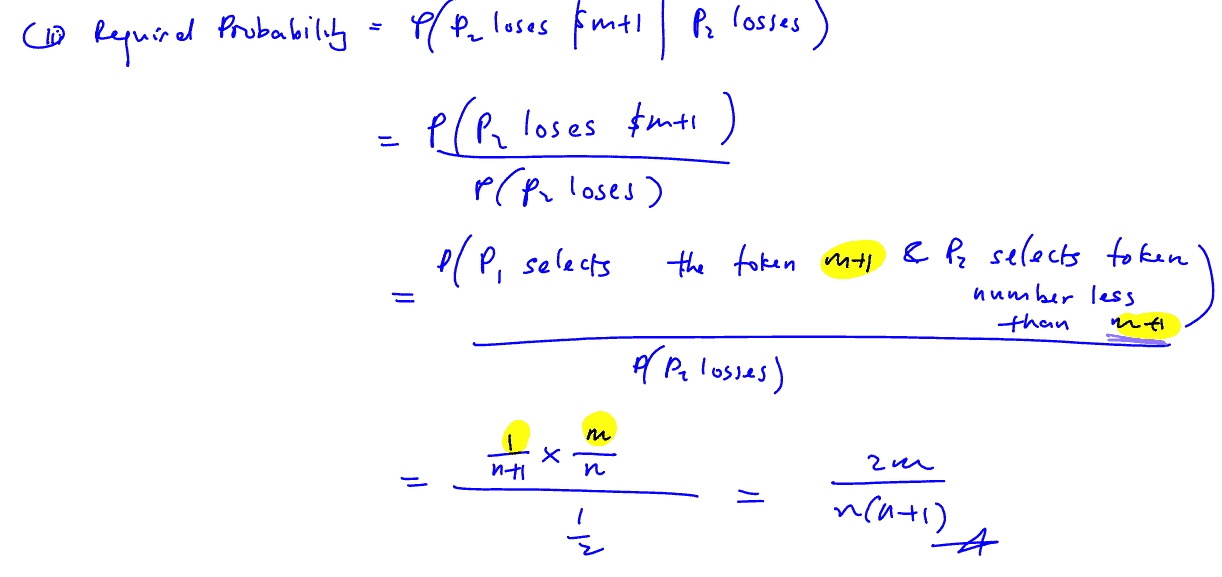
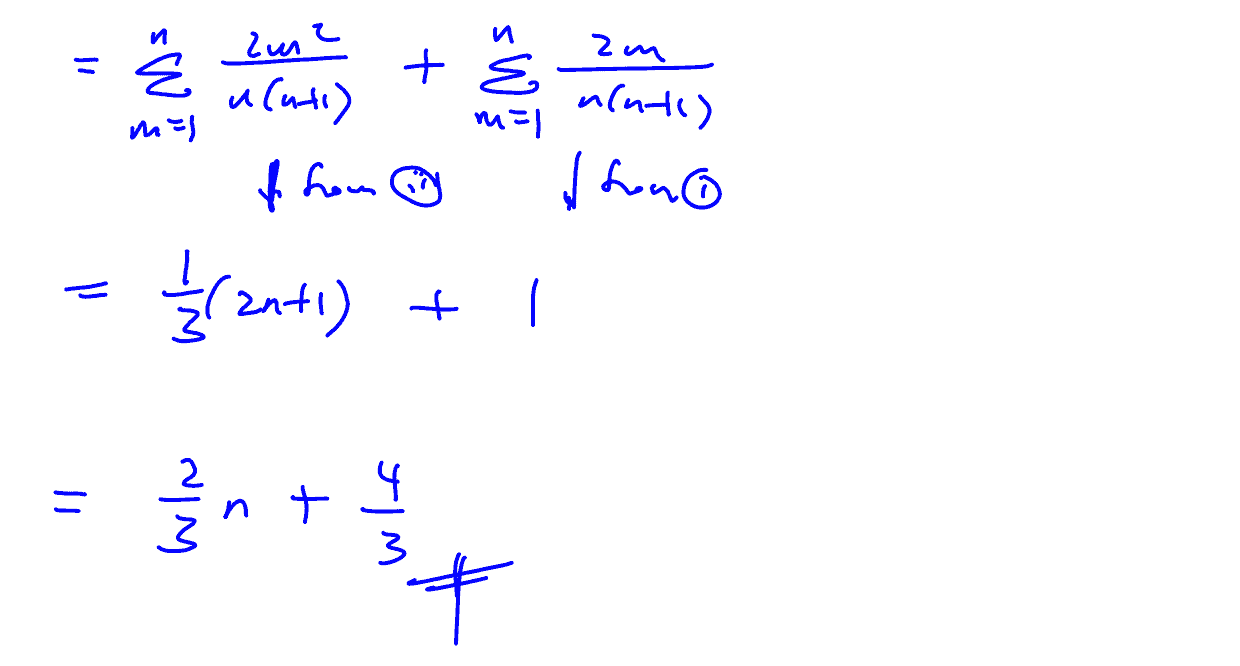
- (i)
- (ii)
- (iii)
- (iv)
- (v)
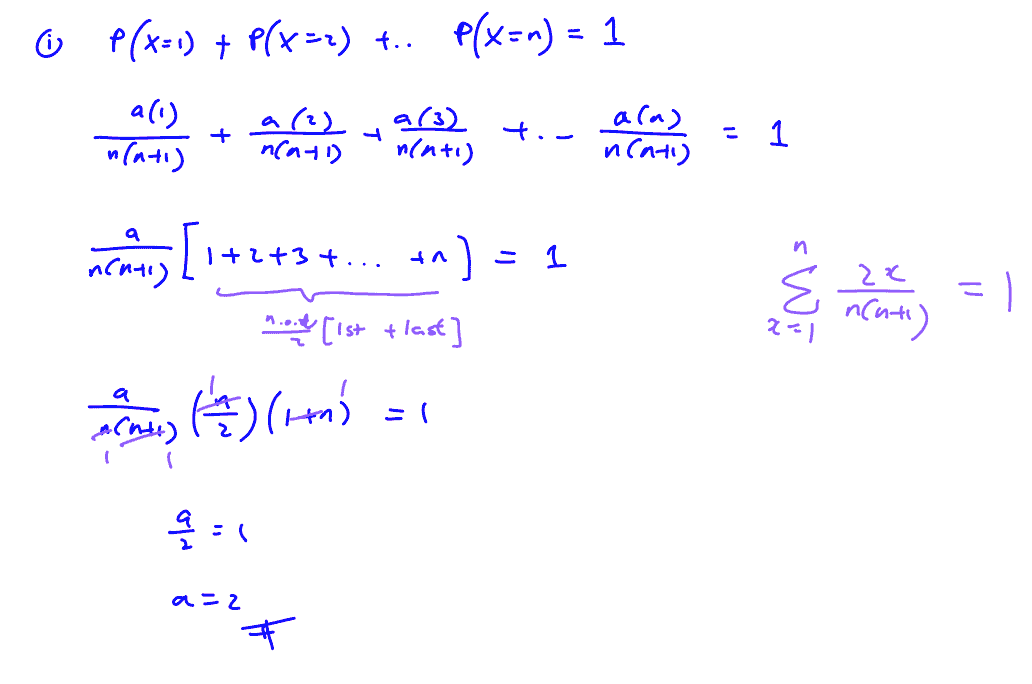
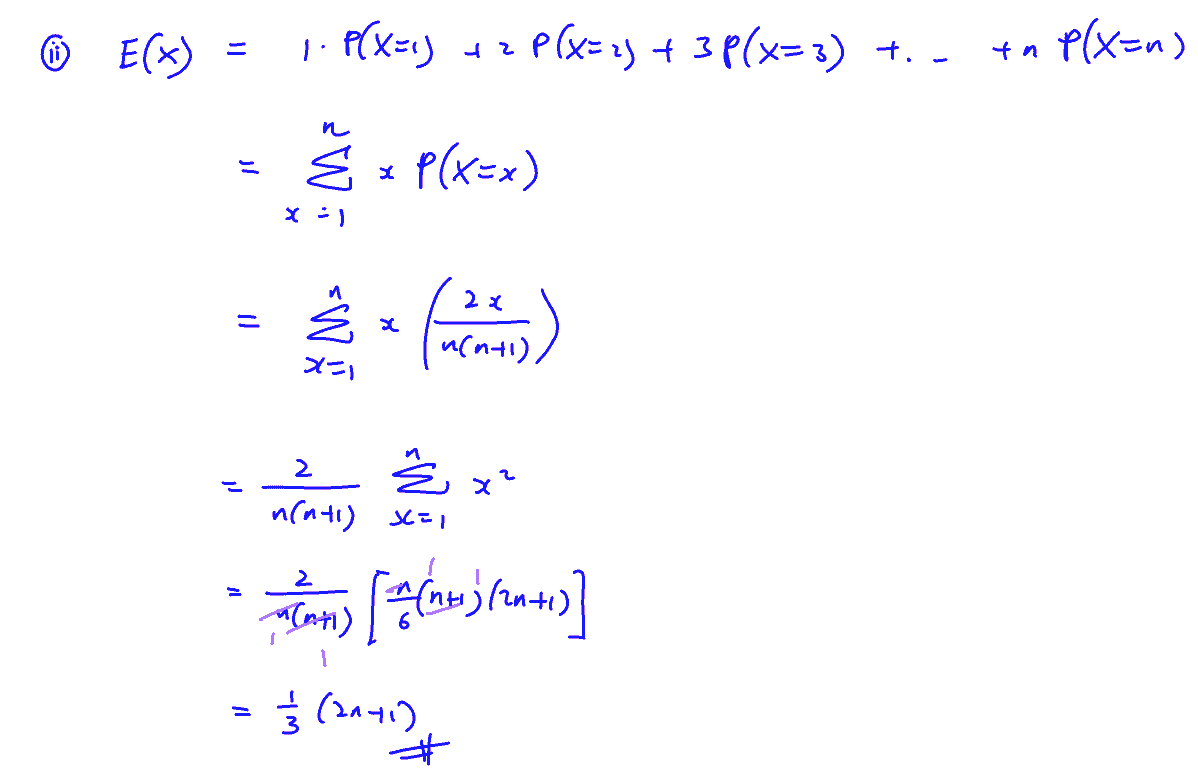
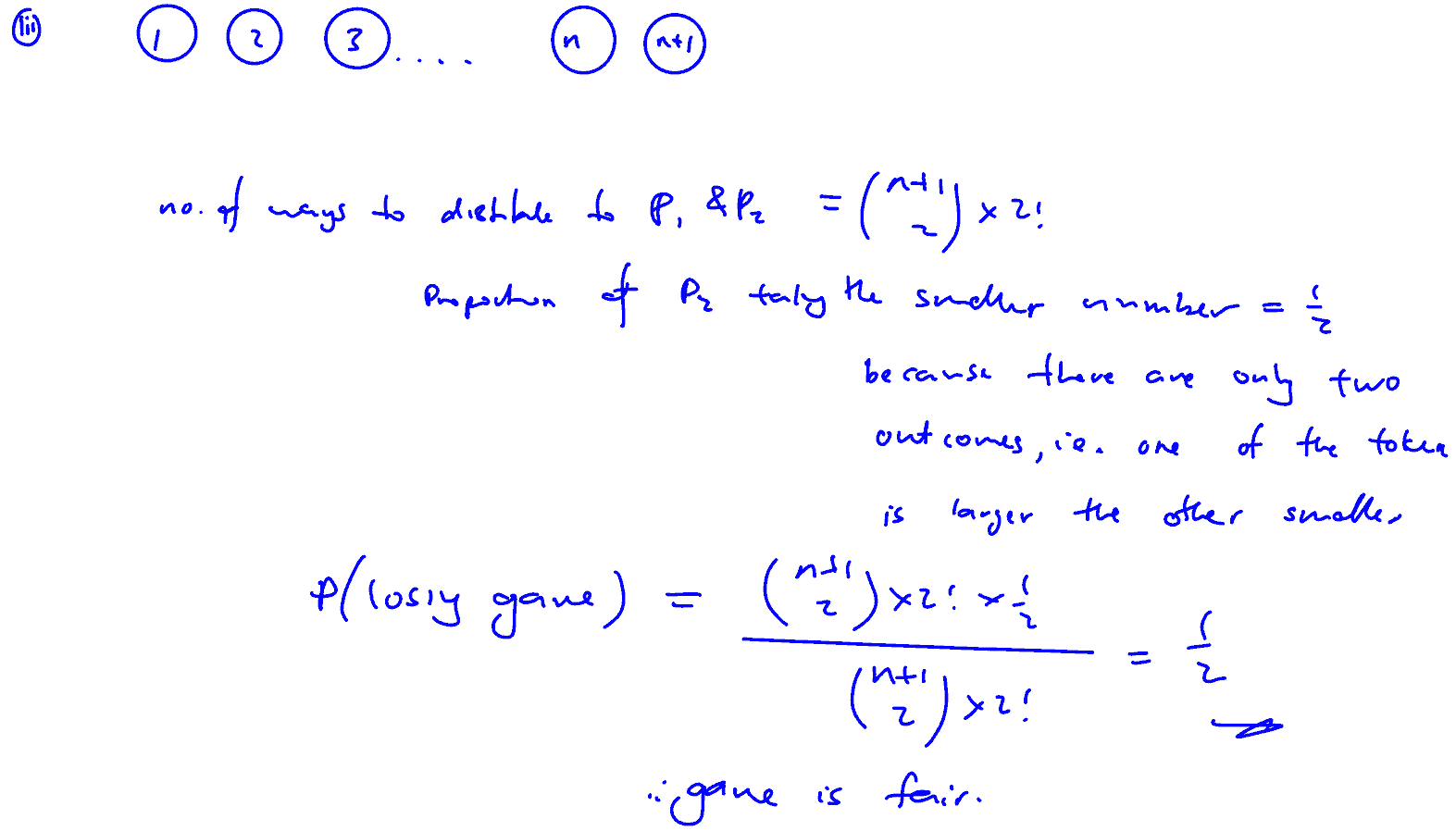
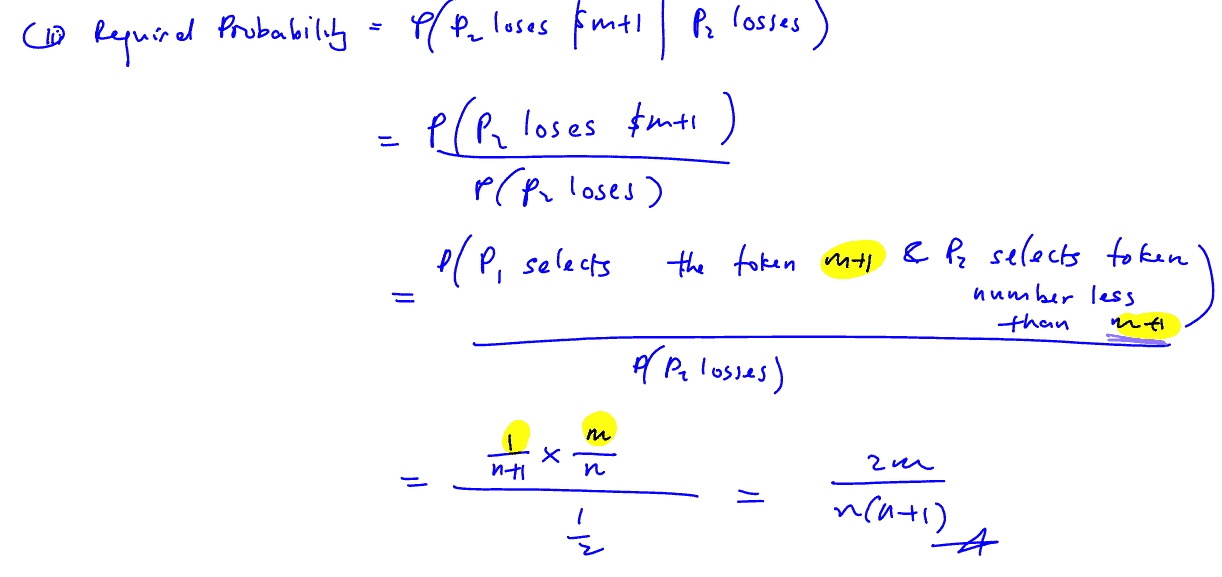
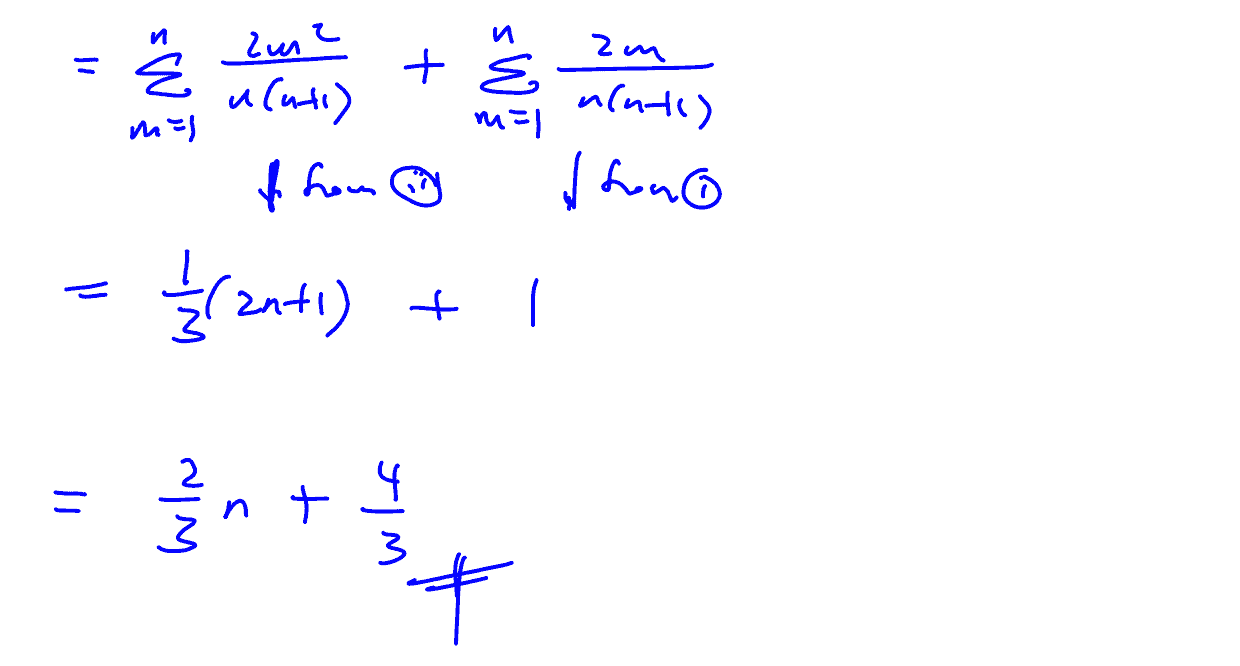
Share with your friends!
Discrete Random Variable – Probability Involving Proportionality
Four rods of lengths $1$, $2$, $3$ and $4$ units are placed in a bag from which one rod is selected at random. The probability of selecting a rod of length $l$ is $kl$. Find the value of $k$.
Show that the expected value of $X$, the length of the selected rod, is $3$ units and the variance of $X$.
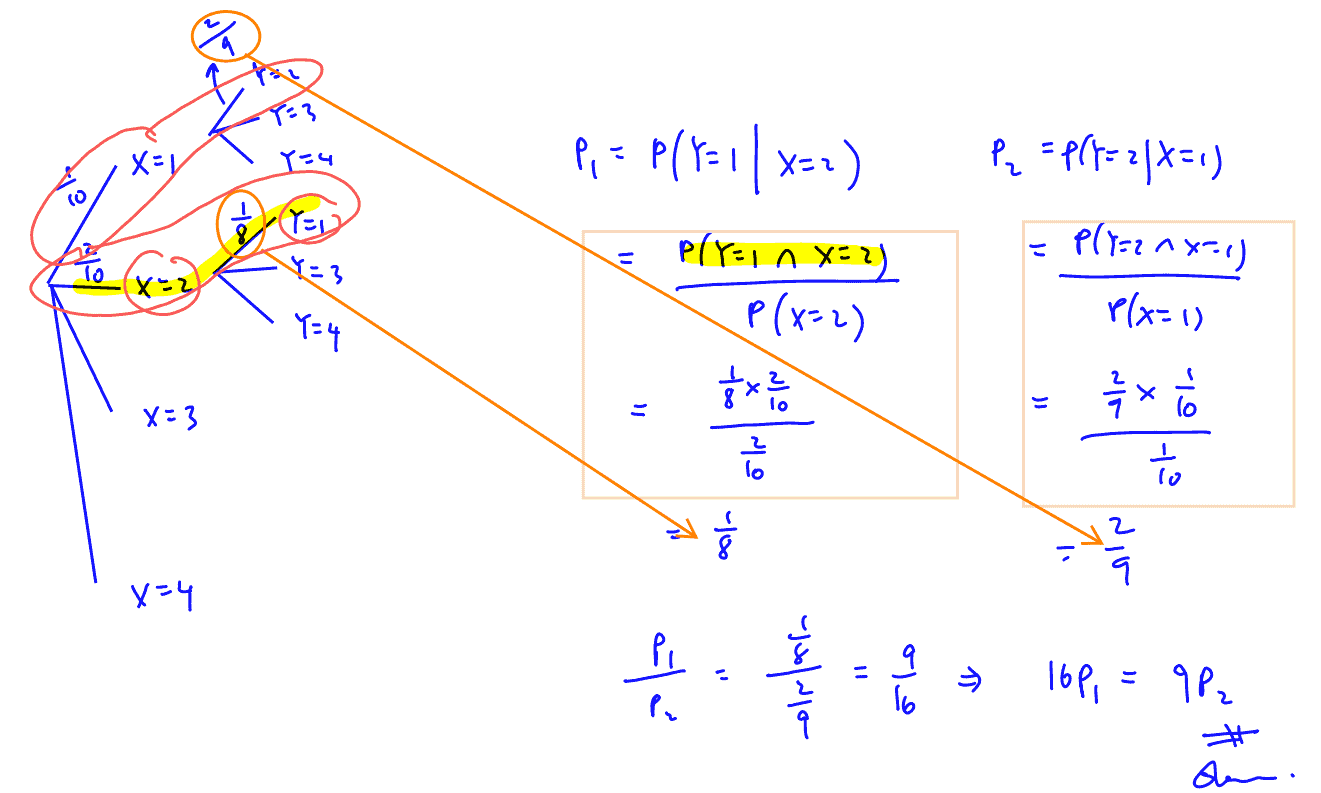
After a rod has been selected it is not replaced. The probabilities of selection for each of the three rods remain are in the same ratio as they were before the first selection. A second rod is now selected from the bag. Defining $Y$to be the length of the rod and writing ${{P}_{1}}=\text{P}\left( Y=1|X=2 \right)$, ${{P}_{2}}=\text{P}\left( Y=2|X=1 \right)$ show that $16{{P}_{1}}=9{{P}_{2}}$
Show also that $\text{P}\left( X+Y=3 \right)=\frac{17}{360}$.
Suggested Handwritten and Video Solutions
- I
- II
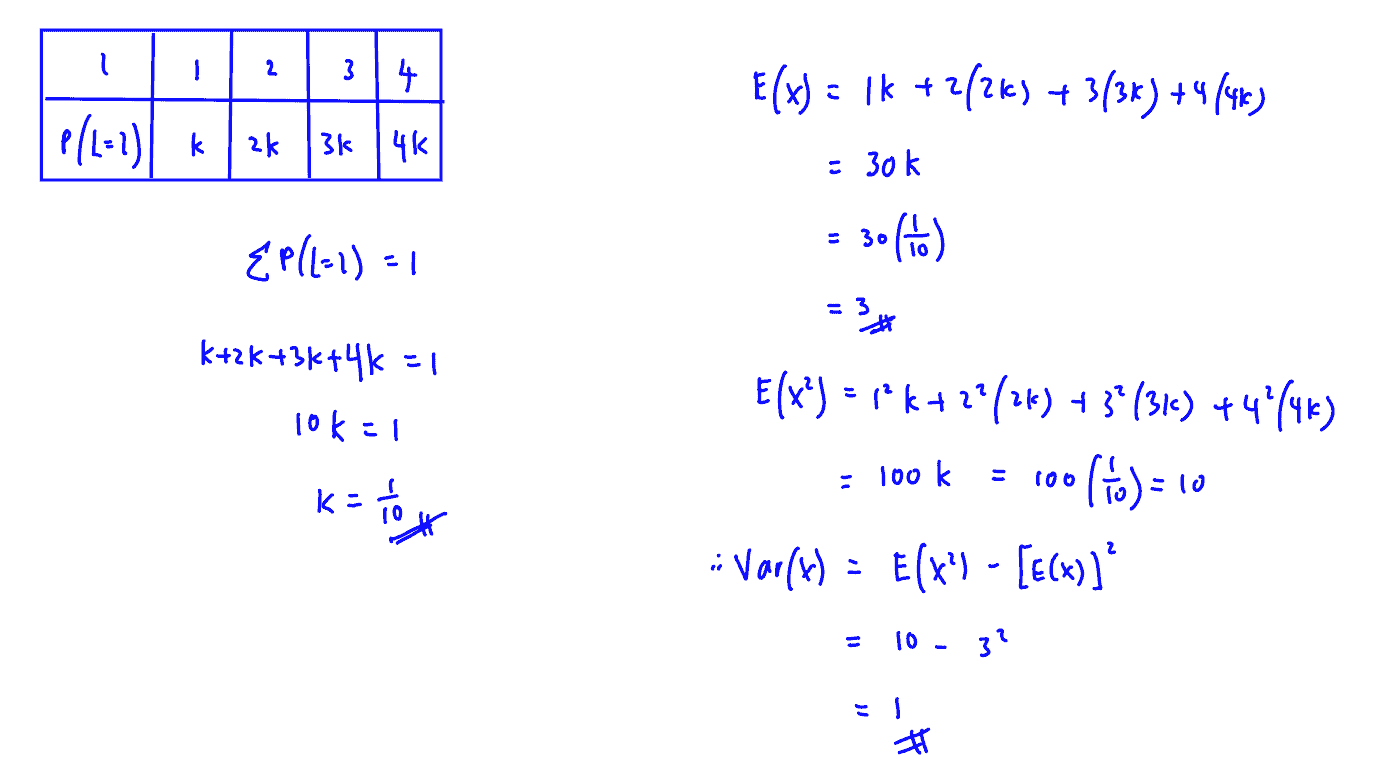
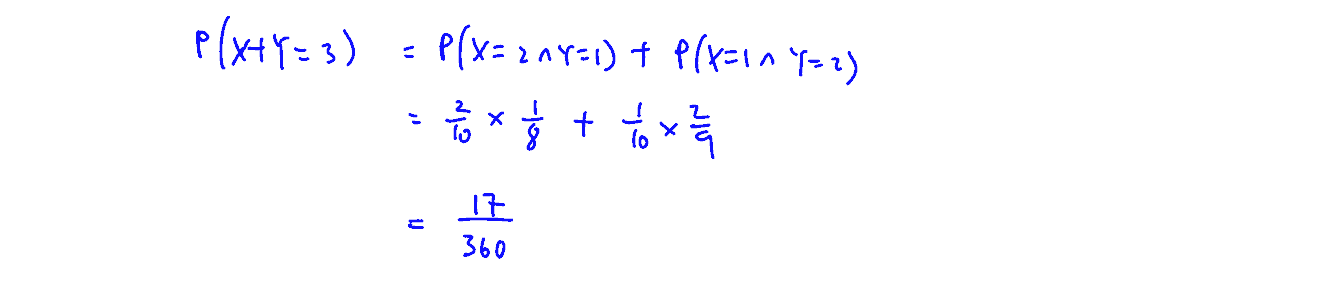
- I
- II
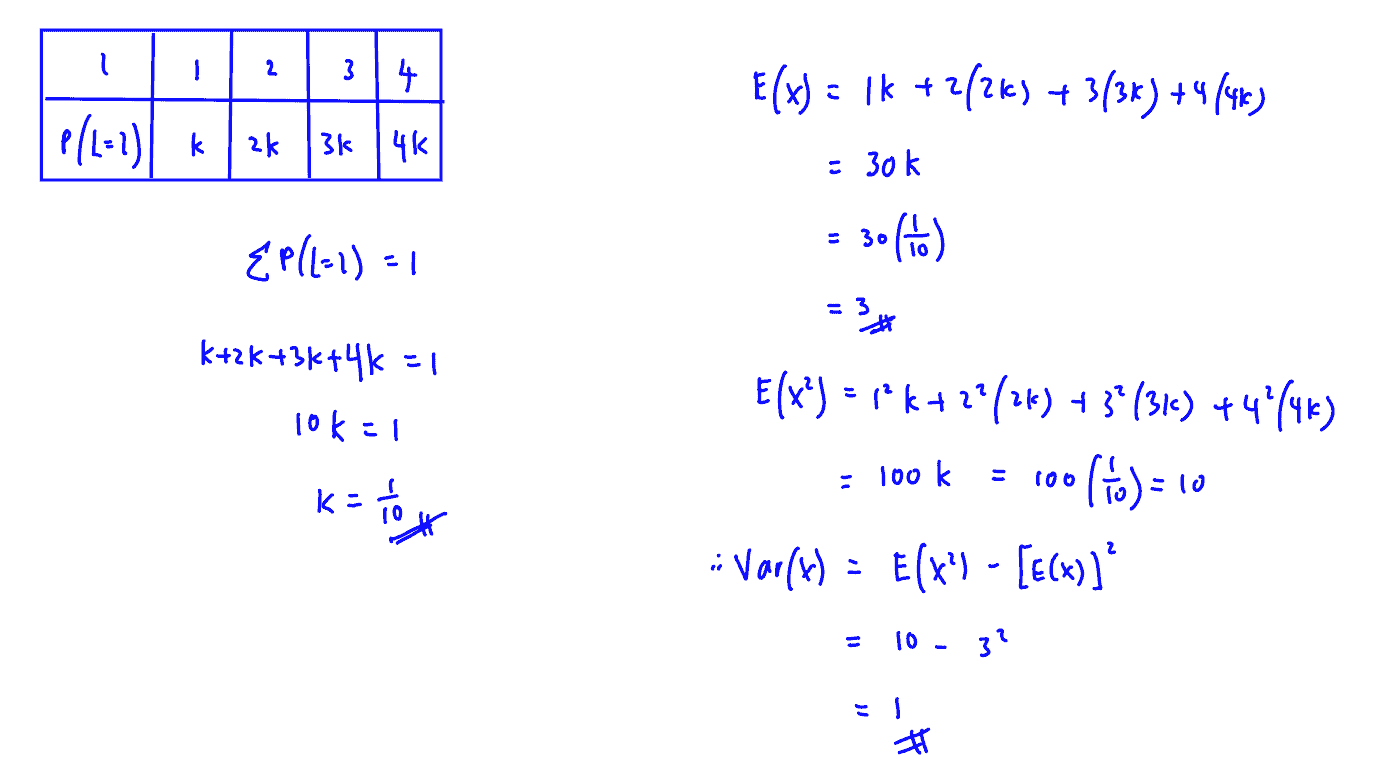

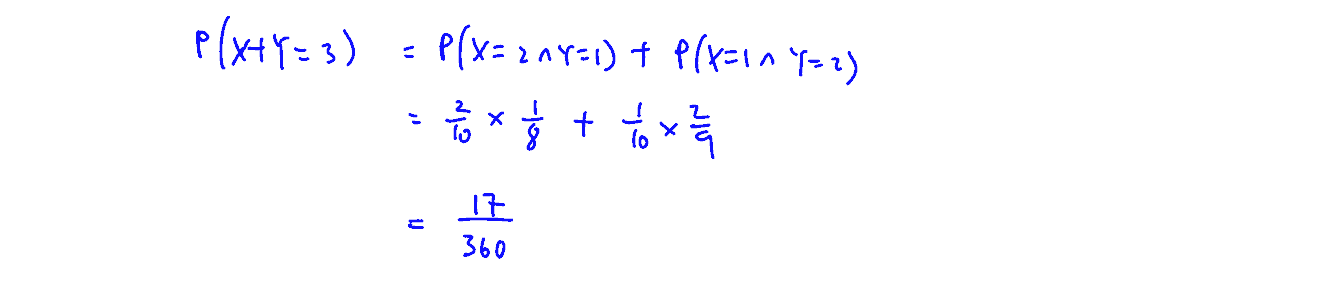
Share with your friends!
2018 RI CT3 J2 Q13
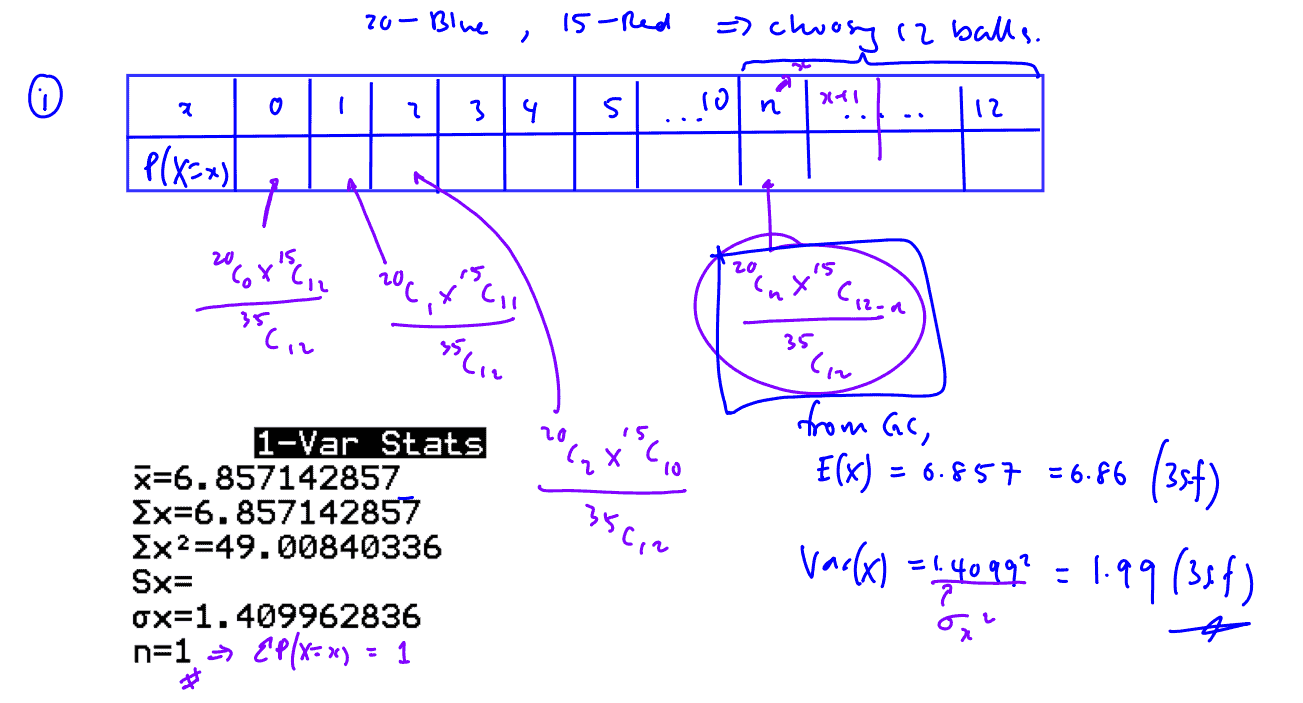
A bag contains $20$ blue balls and $15$ red balls. In a game, Joe draws $12$ balls one by one, at random and without replacement. The number of blue balls Joe draws from the bag is denoted by $X$.
(i)
Find $\text{E}\left( X \right)$ and $\text{Var}\left( X \right)$.
[4]
(ii)
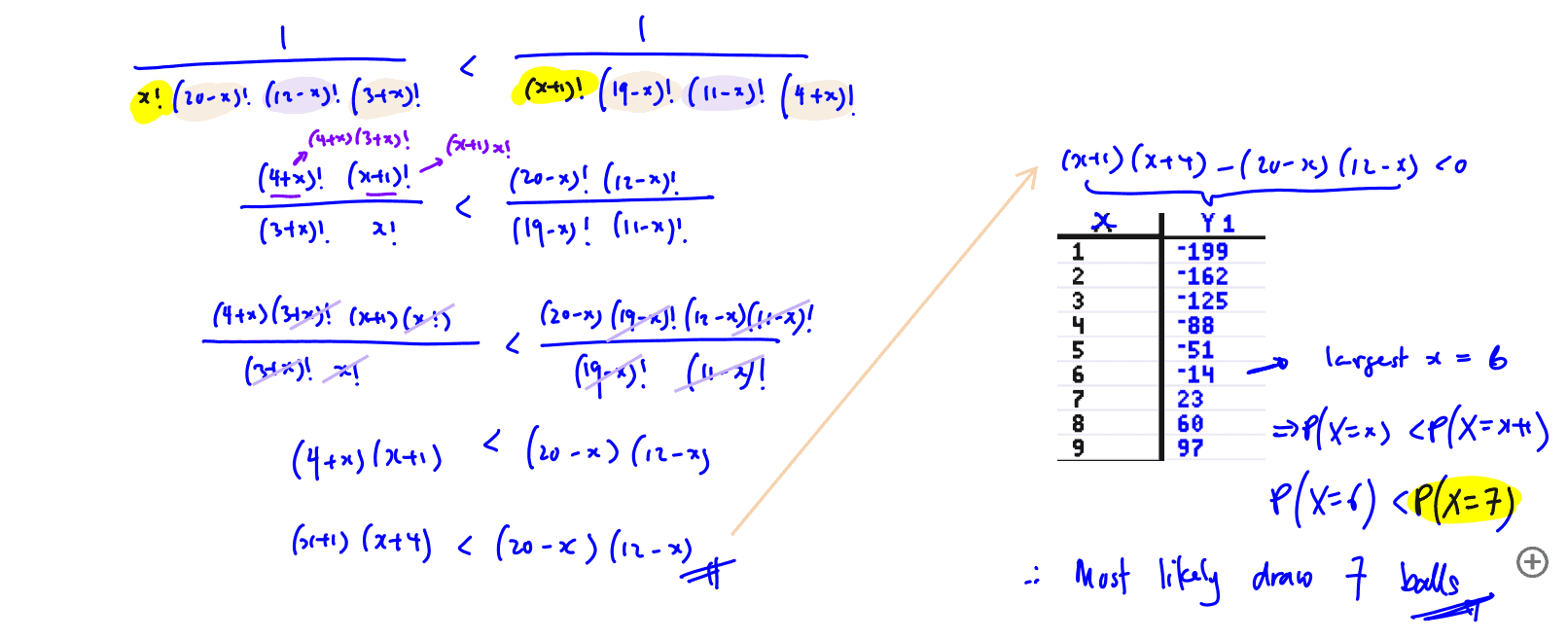
If $\text{P}\left( X=x \right)<\text{P}\left( X=x+1 \right)$, show that $x$ satisfies the inequality
$\left( x+a \right)\left( x+b \right)<\left( c-x \right)\left( d-x \right)$
where $a$, $b$, $c$ and $d$ are constants to be determined. Use this inequality to find the number of blue balls that Joe is most likely to draw.
[5]
Joe plays this game $30$ times.
(iii)
Find the probability that Joe draws at least $10$ blue balls in more than $4$ of his $30$ games.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
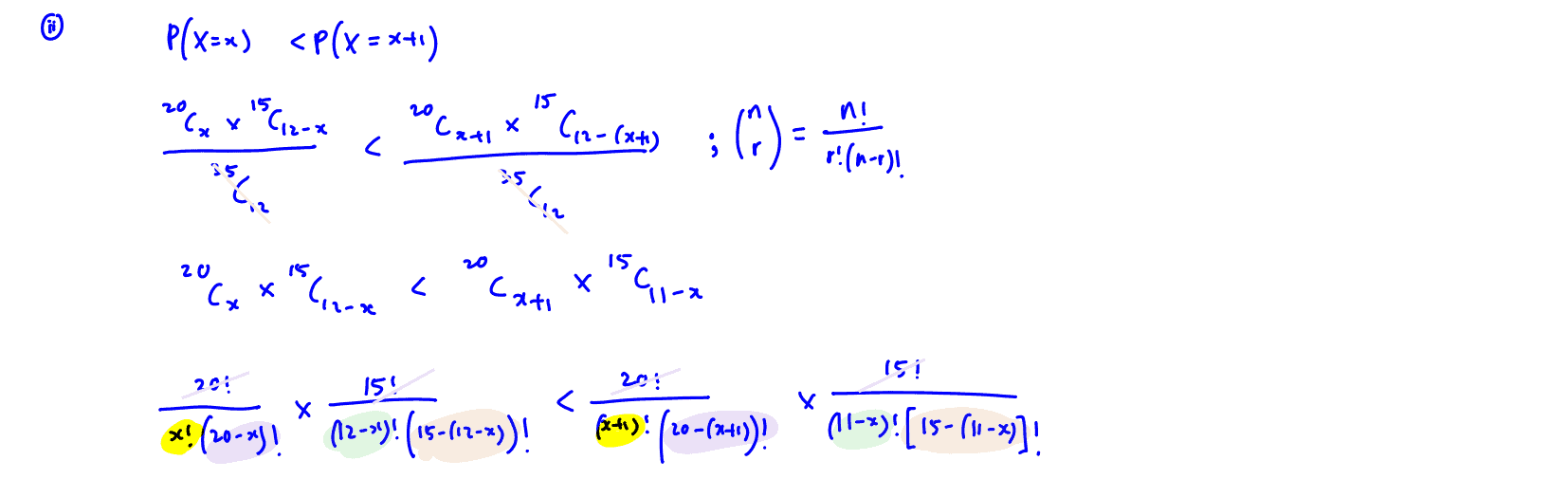
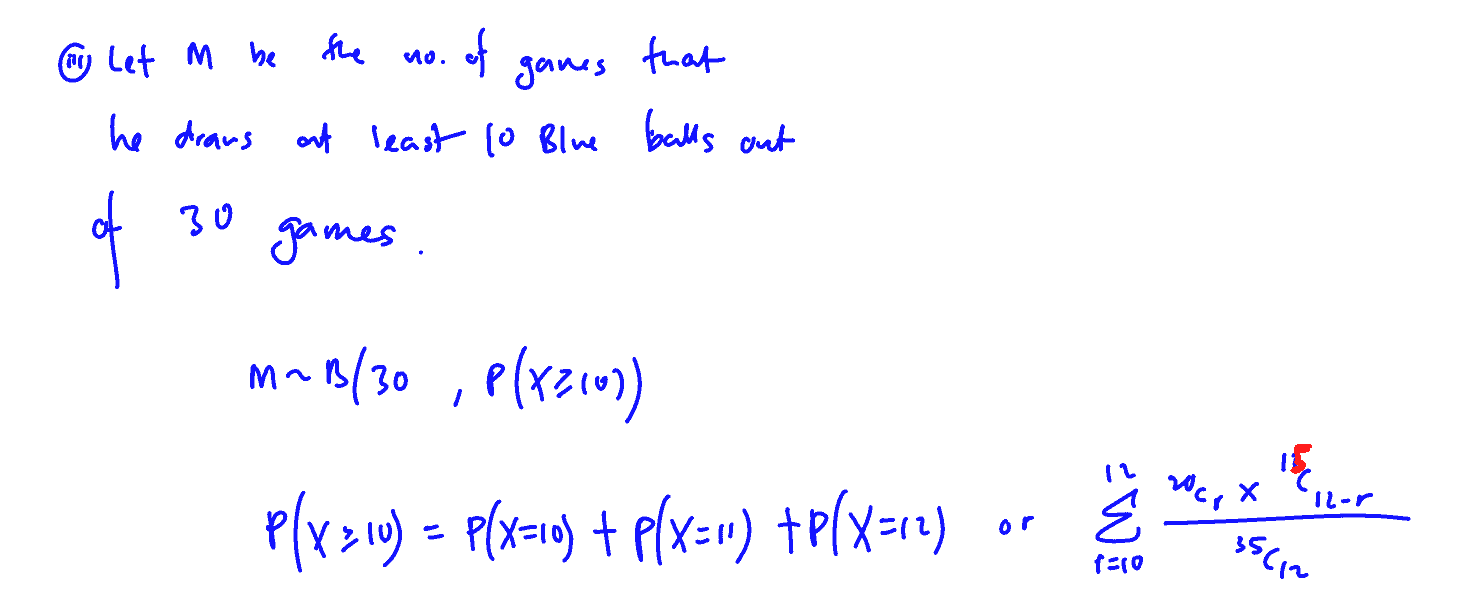
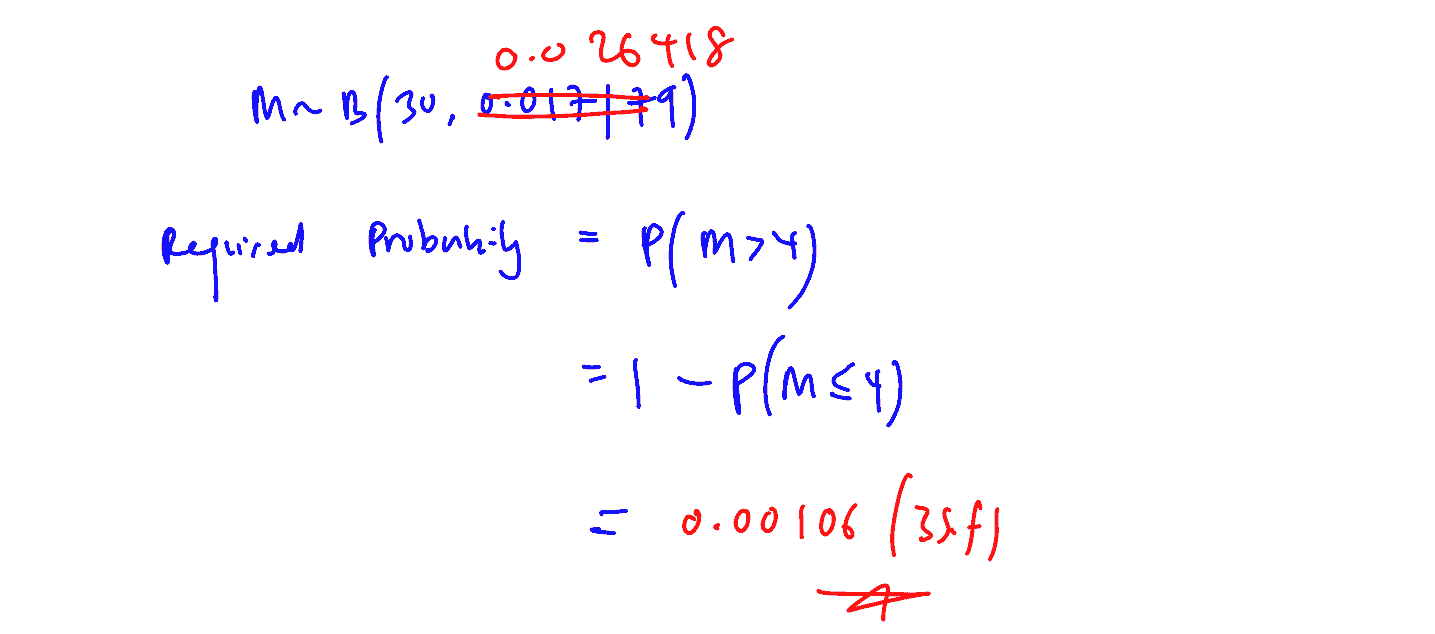
- (i)
- (ii)
- (iii)

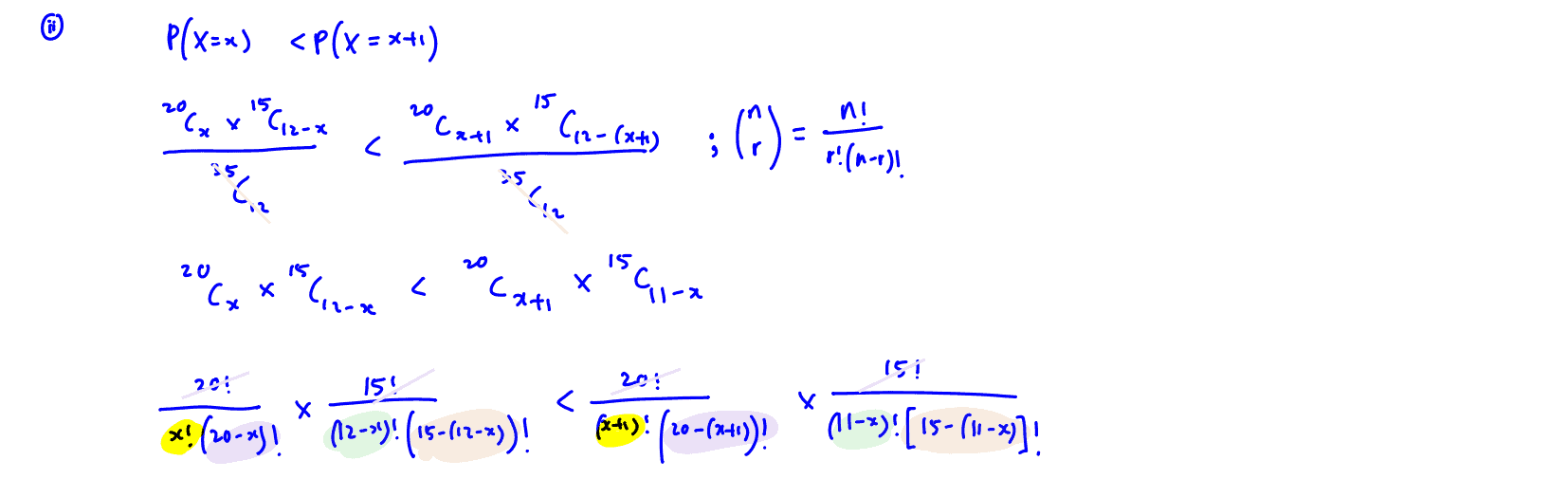

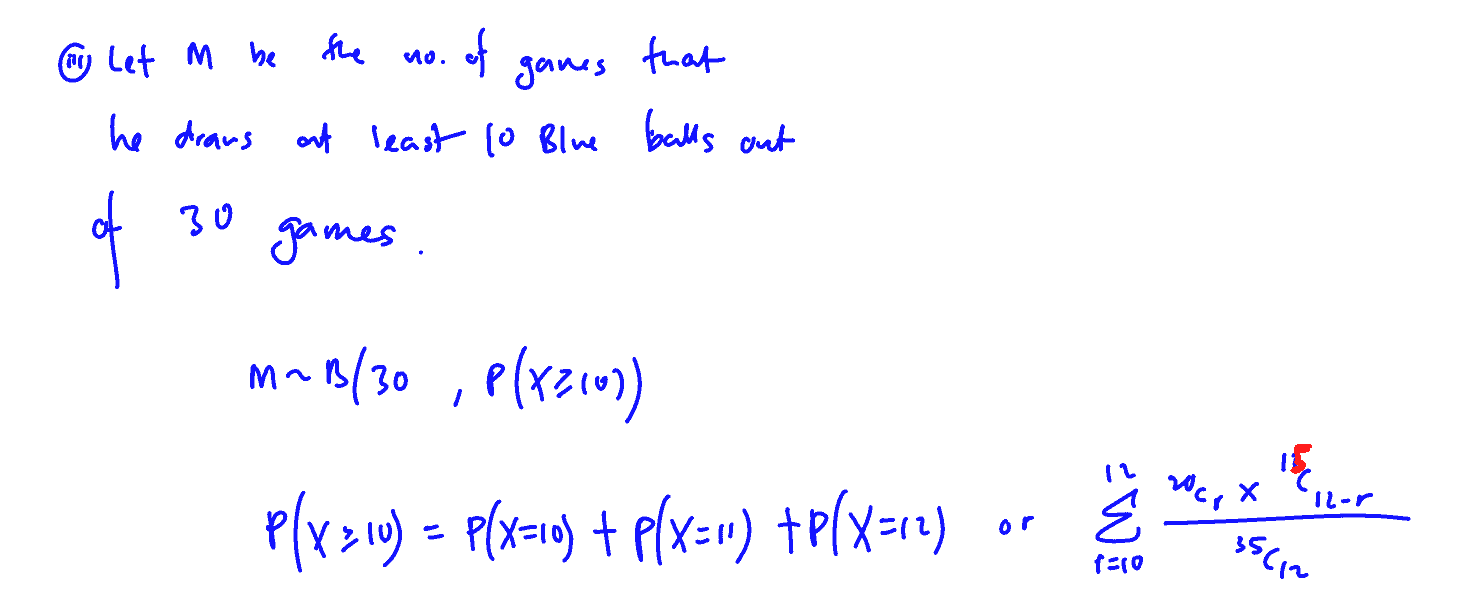
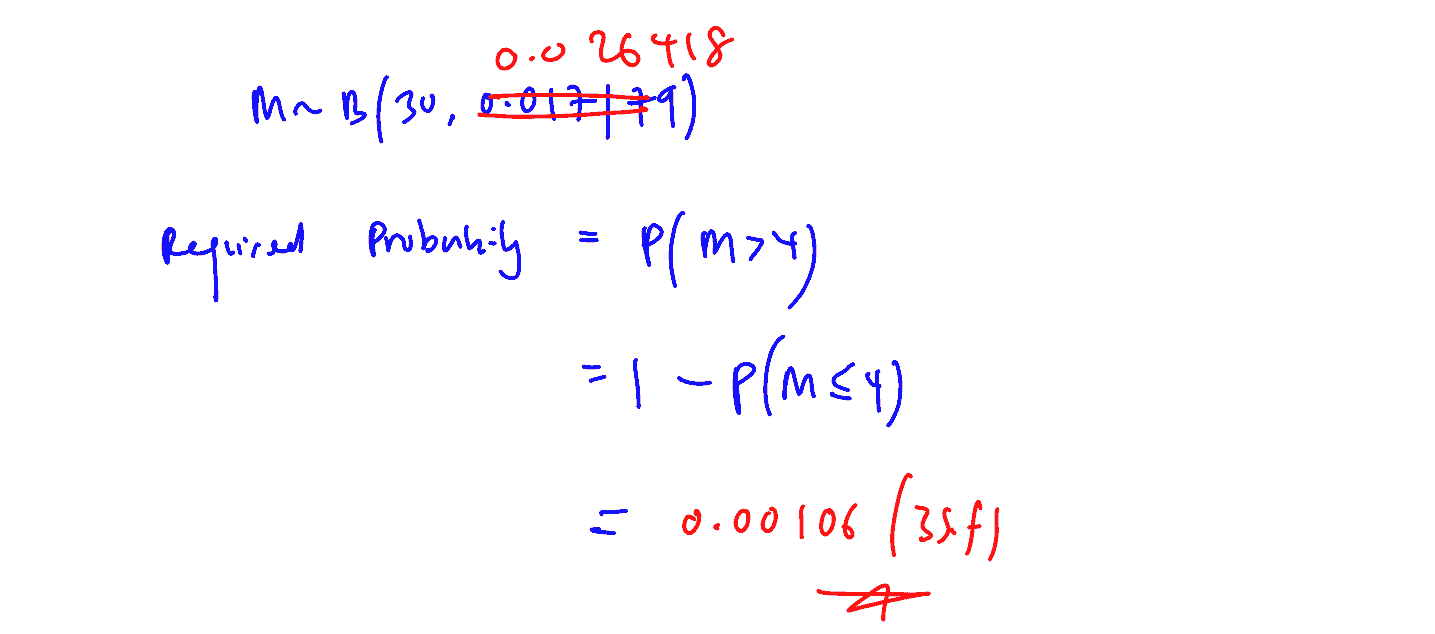
Share with your friends!
Download Discrete Random Variable Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
