A-Level H2 Math | 5 Essential Questions
Functions
In mathematics, the function is a relation that relates the elements from a set (domain) to the elements in another set (codomain). Each element in the domain is related to exactly one element in the codomain. Some of the frequently used functions are quadratic functions, polynomial functions, inverse functions, modulus functions, etc.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2020 YIJC P1 Q7
The functions $\text{f}$ and $\text{g}$ are defined by
$\begin{matrix}
& \text{f}:x\mapsto {{x}^{2}}+3x+1,x\in \mathbb{R},x\le -\frac{3}{2}, \\
& \text{g}:x\mapsto 3+{{\text{e}}^{-x}},x\in \mathbb{R}. \\
\end{matrix}$
(i)
Show that $\text{f}$ has an inverse.
[1]
(i) Show that $\text{f}$ has an inverse.
[1]
(ii)
Give a reason why the composite function ${{\text{f}}^{-1}}\text{g}$ exists. Find ${{\text{f}}^{-1}}\text{g}\left( x \right)$ and state the domain of ${{\text{f}}^{-1}}\text{g}$.
[6]
(ii) Give a reason why the composite function ${{\text{f}}^{-1}}\text{g}$ exists. Find ${{\text{f}}^{-1}}\text{g}\left( x \right)$ and state the domain of ${{\text{f}}^{-1}}\text{g}$.
[6]
The function $\text{h}$ is defined as follows.
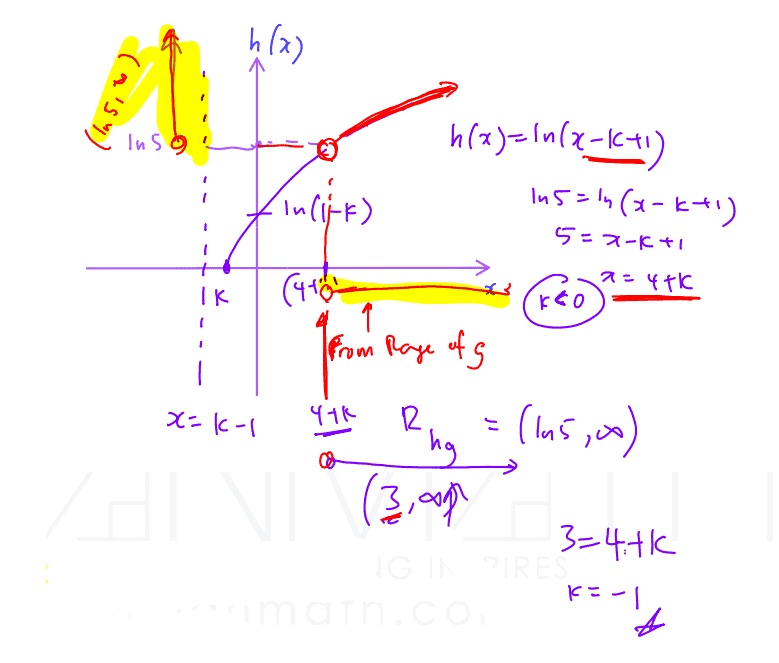
$\text{h}:x\mapsto \ln \left( x-k+1 \right),x\in \mathbb{R},x\ge k,$ where $k<0$.
(iii)
Find the value of $k$ such that the range of $\text{hg}$ is given by $\left( \ln 5,\infty \right)$.
[2]
(iii) Find the value of $k$ such that the range of $\text{hg}$ is given by $\left( \ln 5,\infty \right)$.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
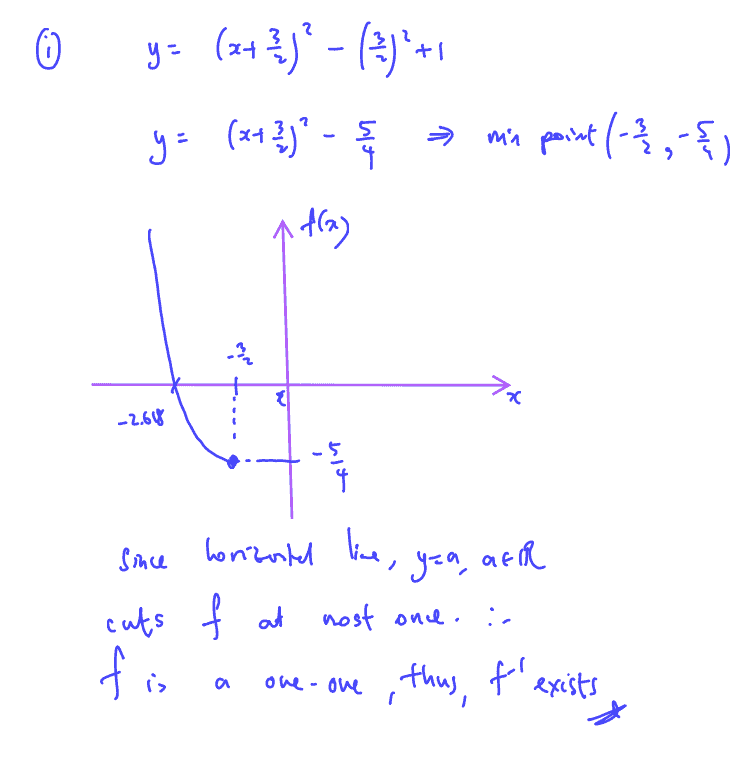
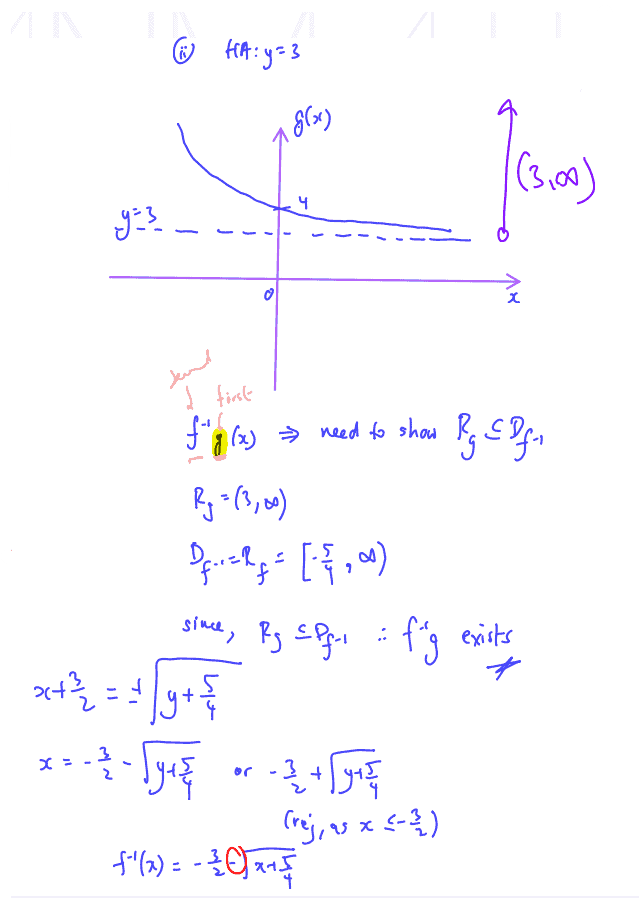
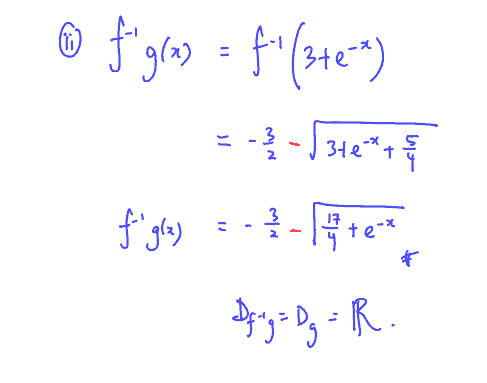
- (i)
- (ii)
- (iii)
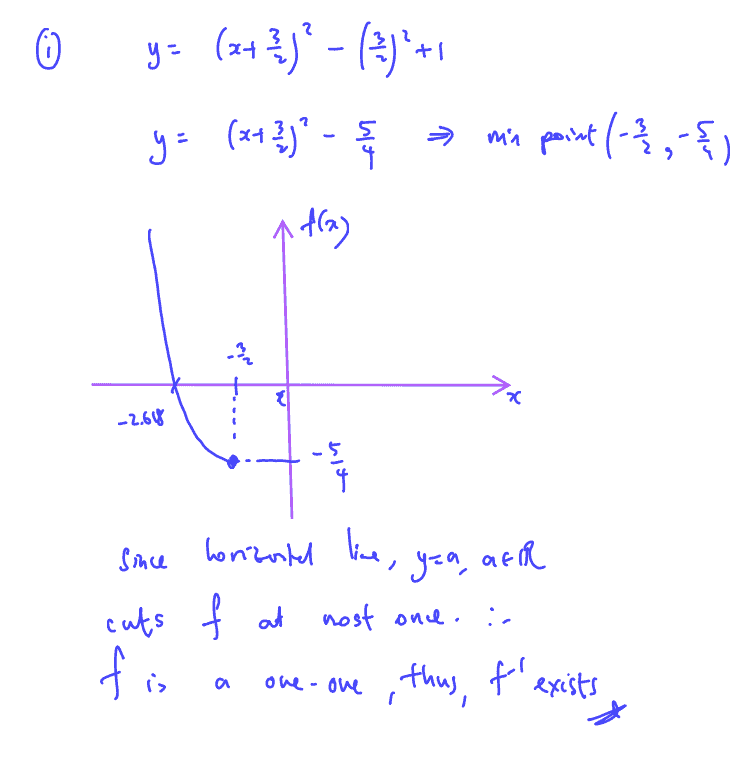
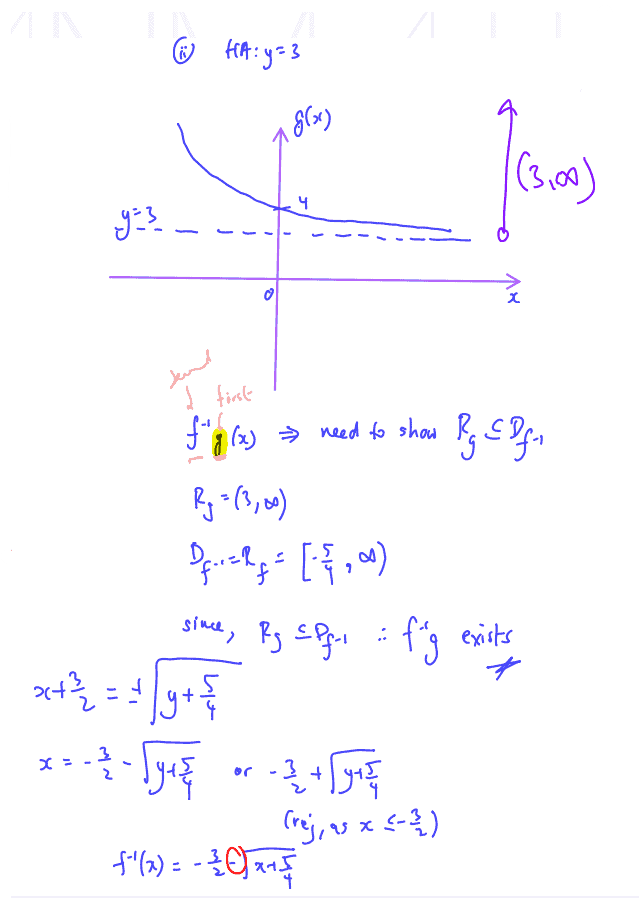
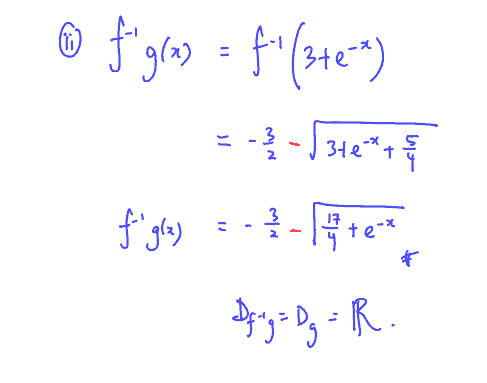

Share with your friends!
2020 DHS Promo Q3
Functions $\text{f}$ and $\text{g}$ are defined by
$\text{f}:x\mapsto {{x}^{2}}+cx+d,x\in \mathbb{R},$ where $c$ and $d$ are constants,
$\text{g}:x\mapsto \ln x,x\in \mathbb{R},x>0$.
(i)
Given that the composite function $\text{gf}$ exists, find an inequality involving $c$ and $d$.
[2]
(i) Given that the composite function $\text{gf}$ exists, find an inequality involving $c$ and $d$.
[2]
For the rest of the question, take $c=2,d=4$.
(ii)
Write down an expression for $\text{gf}\left( x \right)$ and find exactly the range of $\text{gf}$.
[3]
(ii) Write down an expression for $\text{gf}\left( x \right)$ and find exactly the range of $\text{gf}$.
[3]
(iii)
The graph of a function $\text{h}$ is symmetrical about the line $x=k$ if $\text{h}\left( x+k \right)=\text{h}\left( -x+k \right)$ for all valid values of $x$. Using this definition, show that the graph of $\text{gf}$ is symmetrical about the line $x=-1$.
[2]
(iii) The graph of a function $\text{h}$ is symmetrical about the line $x=k$ if $\text{h}\left( x+k \right)=\text{h}\left( -x+k \right)$ for all valid values of $x$. Using this definition, show that the graph of $\text{gf}$ is symmetrical about the line $x=-1$.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)

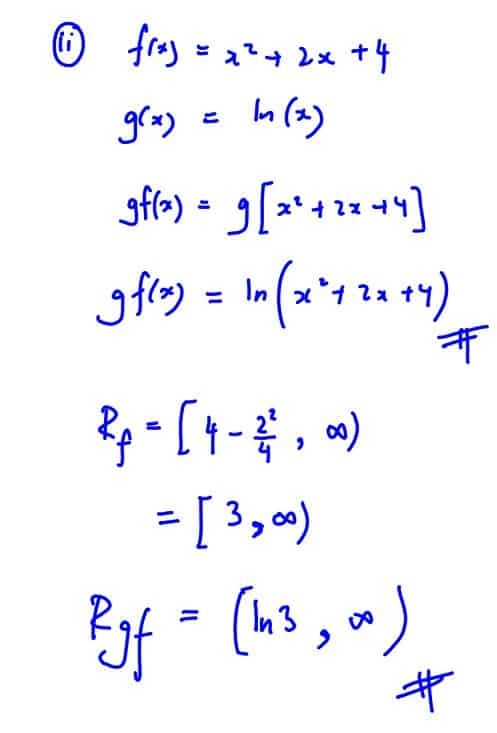
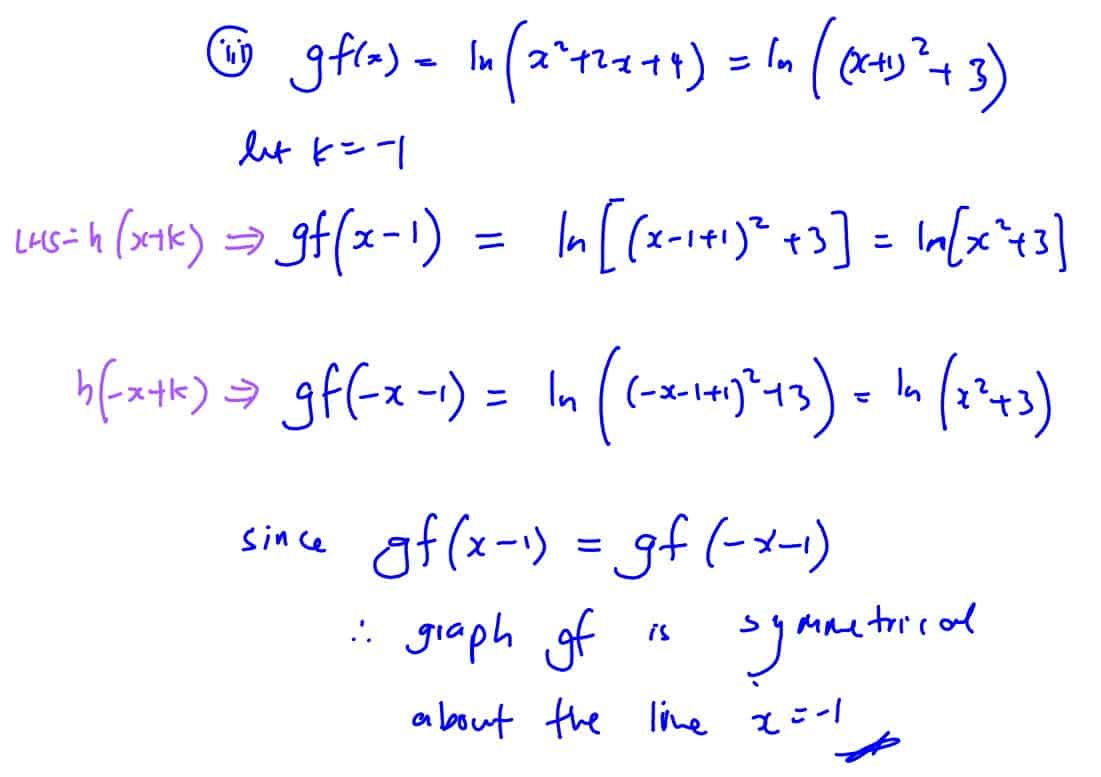
- (i)
- (ii)
- (iii)

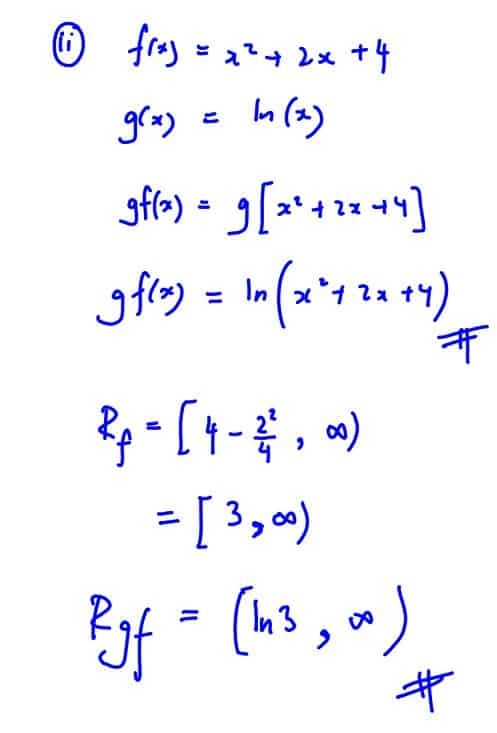
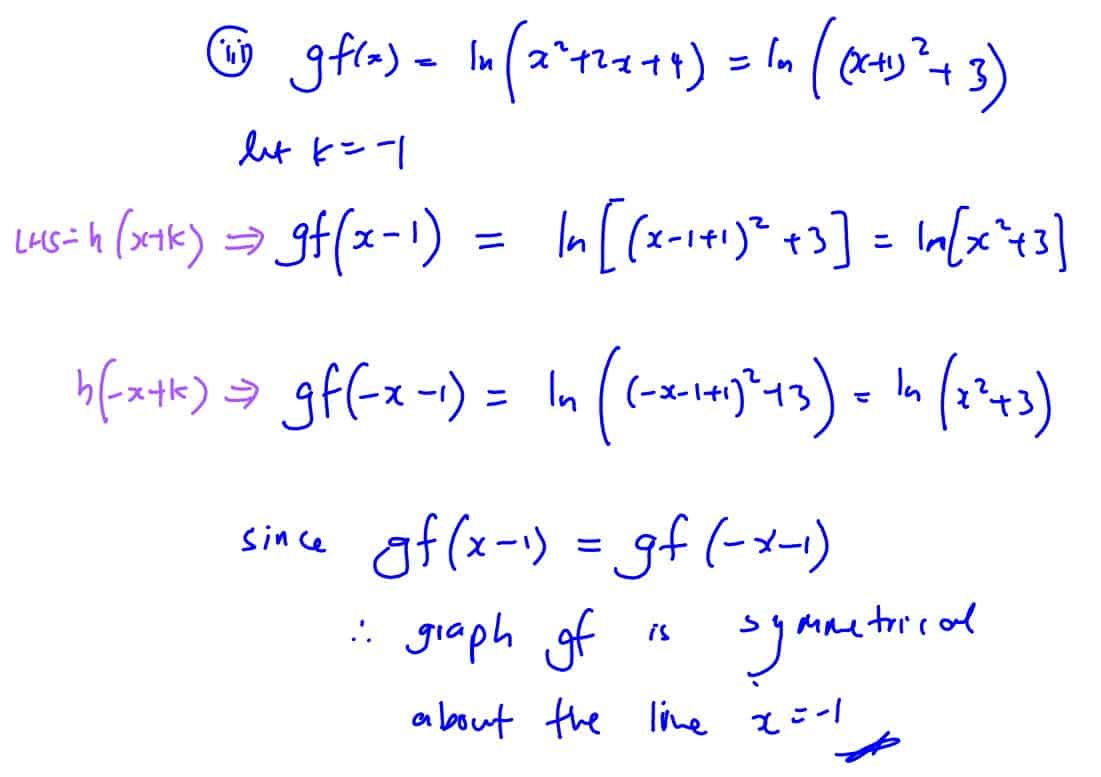
Share with your friends!
2020 TMJC Promo Q7
$\text{f}:x\mapsto -\ln (x-2)$, $x\in \mathbb{R}$, $2<x\le 3$.
(i)
[4]
(i) Find ${{\text{f}}^{-1}}(x)$ and state the domain and range of ${{\text{f}}^{-1}}$.
[4]
(ii)
[6]
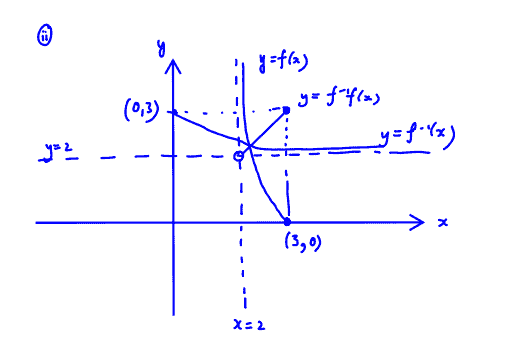
(ii) Sketch on the same diagram the graphs of $y=\text{f}(x)$, $y={{\text{f}}^{-1}}(x)$ and $y={{\text{f}}^{-1}}\text{f}(x)$, giving the equations of any asymptotes and the exact coordinates of any points where the curves cross the $x$- and $y$- axes.
[6]
(iii)
$x+\ln (x-2)=0$,
and find the value of this $x$-coordinate.[2]
(iii) Explain why the x-coordinate of the point of intersection of the graph of $y=\text{f}(x)$ and $y={{\text{f}}^{-1}}(x)$ satisfies the equation
$x+\ln (x-2)=0$,
and find the value of this $x$-coordinate.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
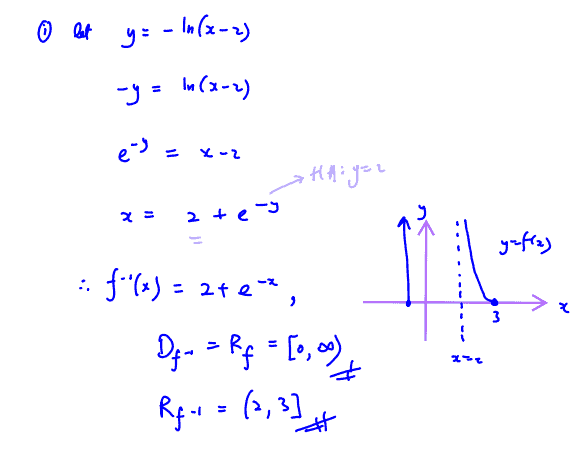
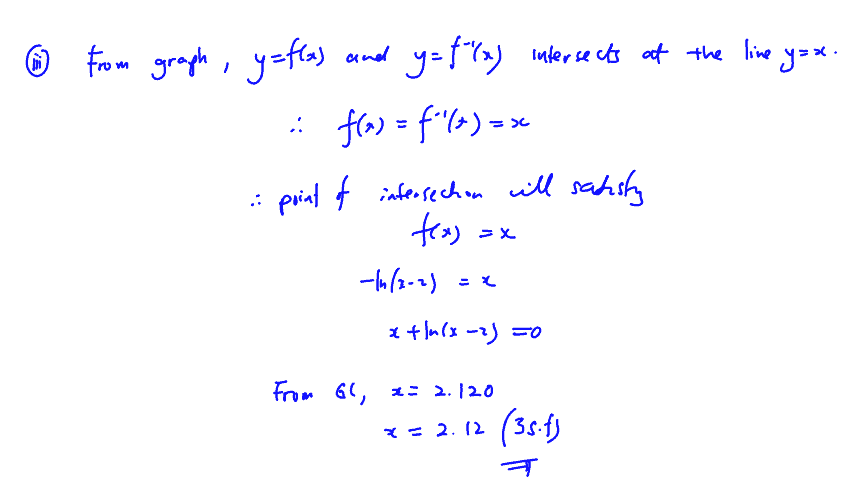
- (i)
- (ii)
- (iii)
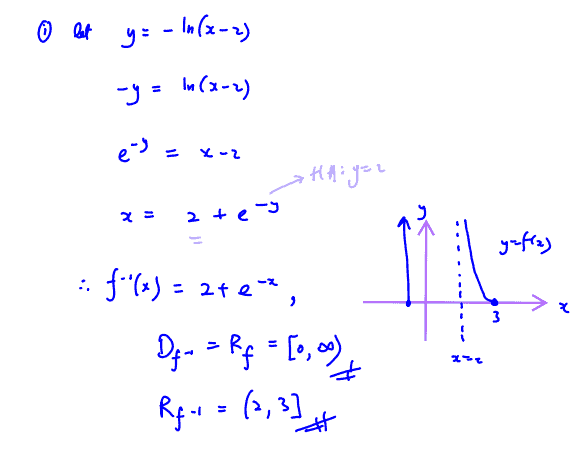

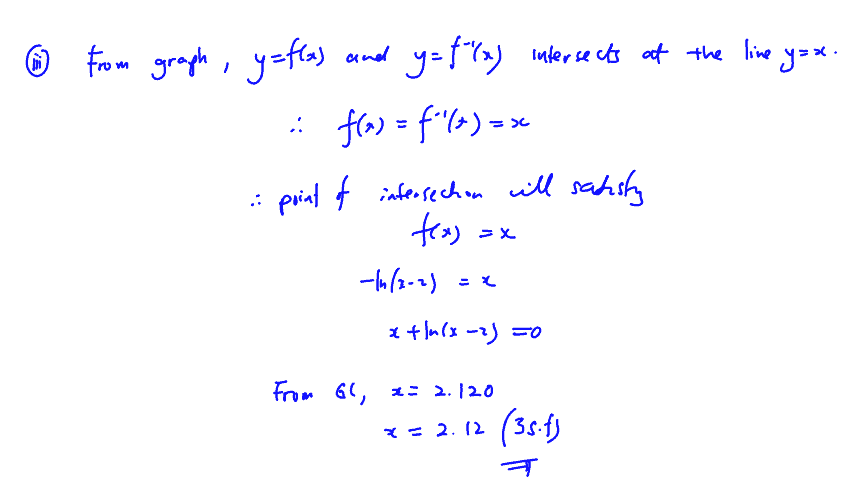
Share with your friends!
2020 EJC Promo Q10
Functions $\text{f}$ and $\text{g}$ are defined by
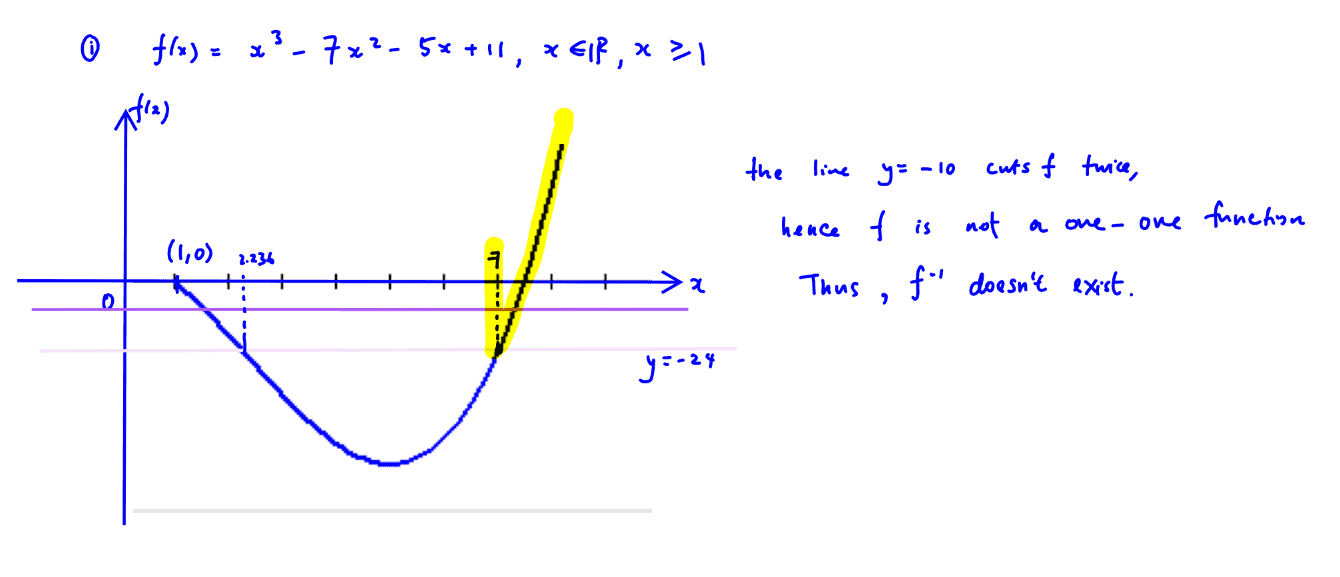
$\text{f}:x\mapsto {{x}^{3}}-7{{x}^{2}}-5x+11$, $x\in \mathbb{R}$, $x\ge k$,
$\text{g}:x\mapsto {{\left( x+1 \right)}^{2}}+2$,$x\in \mathbb{R}$.
(i)
Let $k=1$.
(i) Let $k=1$.
(a)
Show that $\text{f}$ does not have an inverse.
[2]
(a) Show that $\text{f}$ does not have an inverse.
[2]
(b)
[2]
(b) Determine whether the composite function $\text{fg}$ exists.
[2]
(ii)
[2]
(ii) Find the value of $k$ given that ${{\text{f}}^{-1}}$ exists and that the domain of ${{\text{f}}^{-1}}$ is $x\in \mathbb{R}$, $x\ge -24$.
[2]
(iii)
Let $k=6$.
(iii) Let $k=6$.
(a)
Show algebraically that $\text{f}'(x)>0$ for all values of $x$ in the domain of $\text{f}$.
[2]
[2]
(b)
Solve the equation $\text{g}{{\text{f}}^{-1}}(x)=83$.
[3]
(b) Solve the equation $\text{g}{{\text{f}}^{-1}}(x)=83$.
[3]
Suggested Handwritten and Video Solutions
- (i)(a)
- (i)(b)
- (ii)
- (iii)(a)
- (iii)(b)
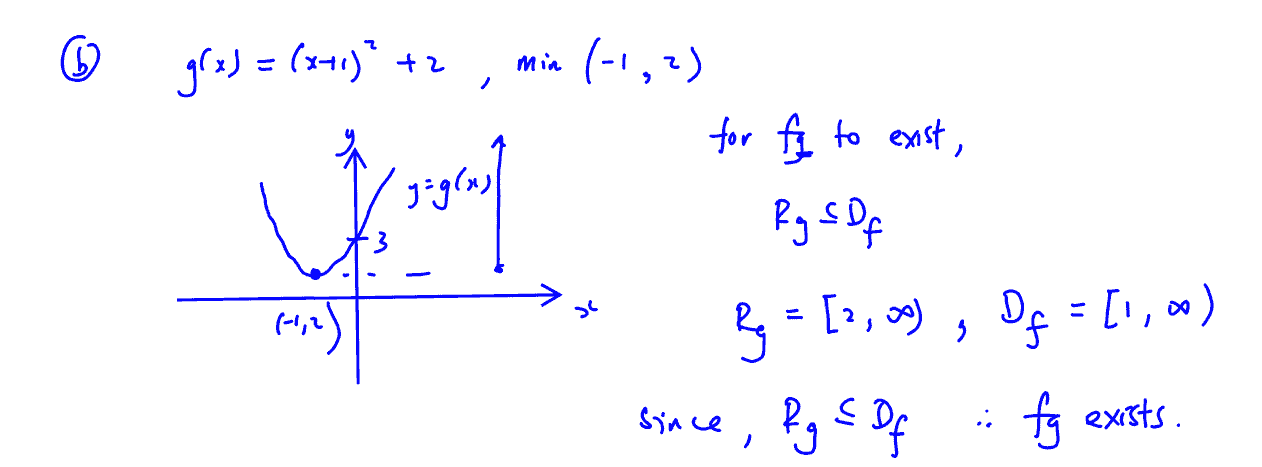
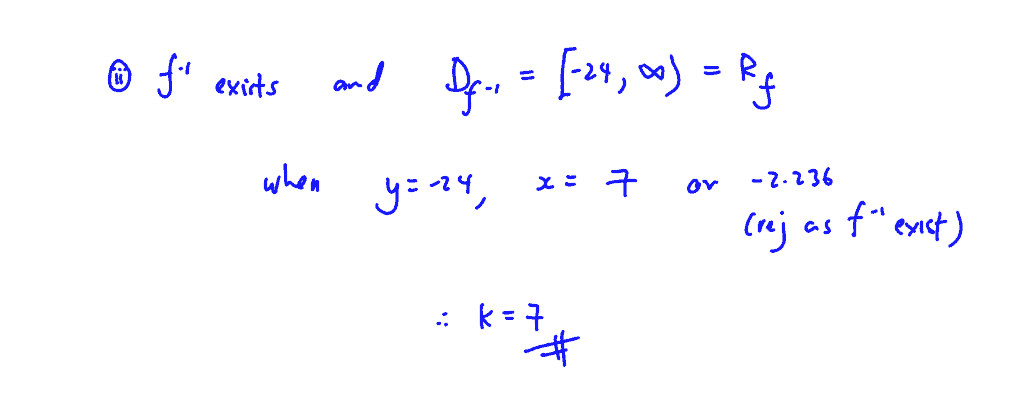
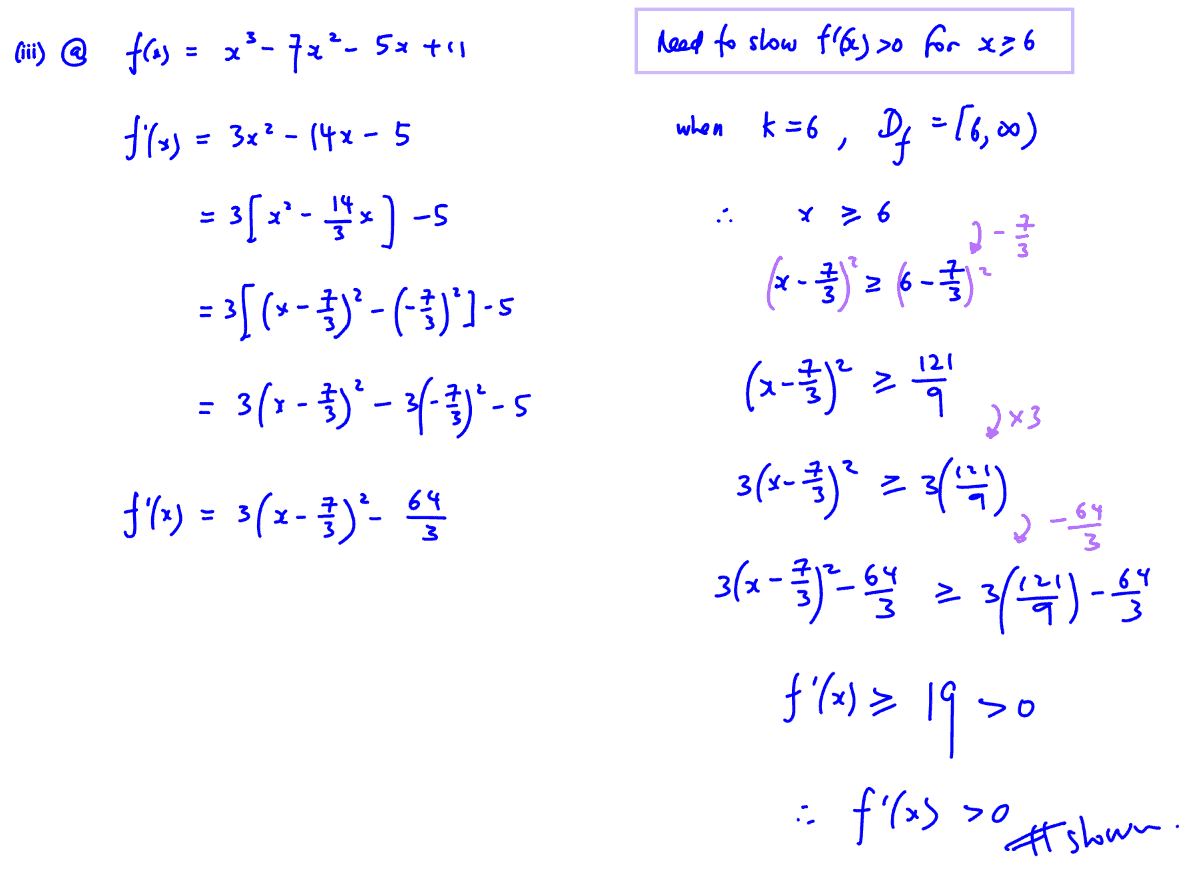
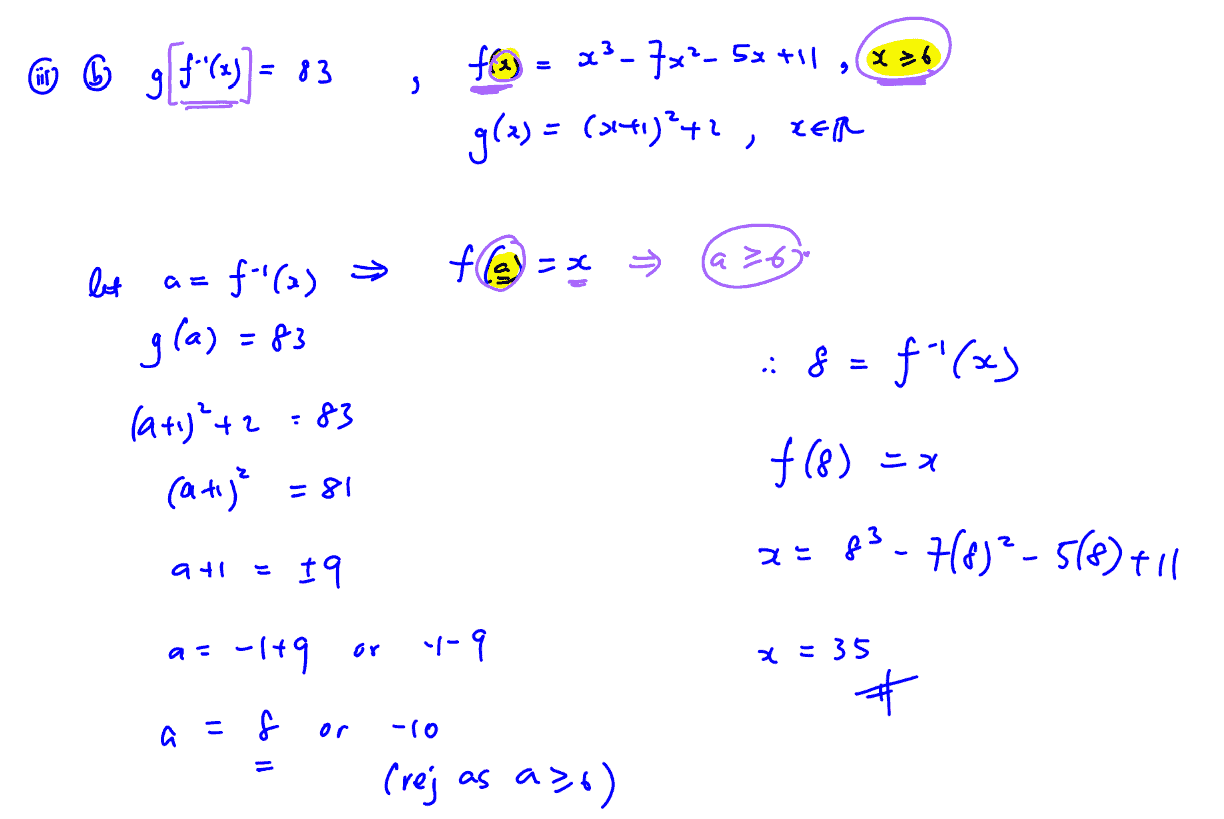
- (i)(a)
- (i)(b)
- (ii)
- (iii)(a)
- (iii)(b)

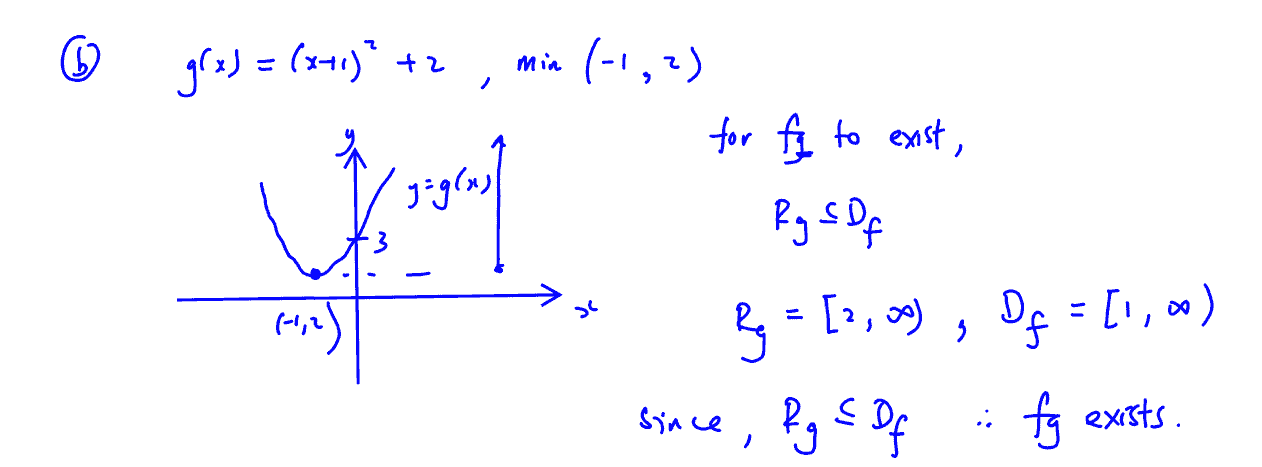
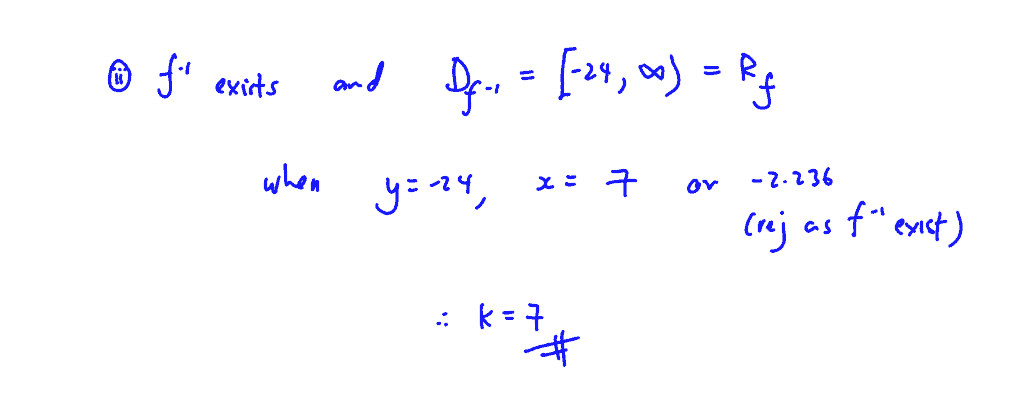
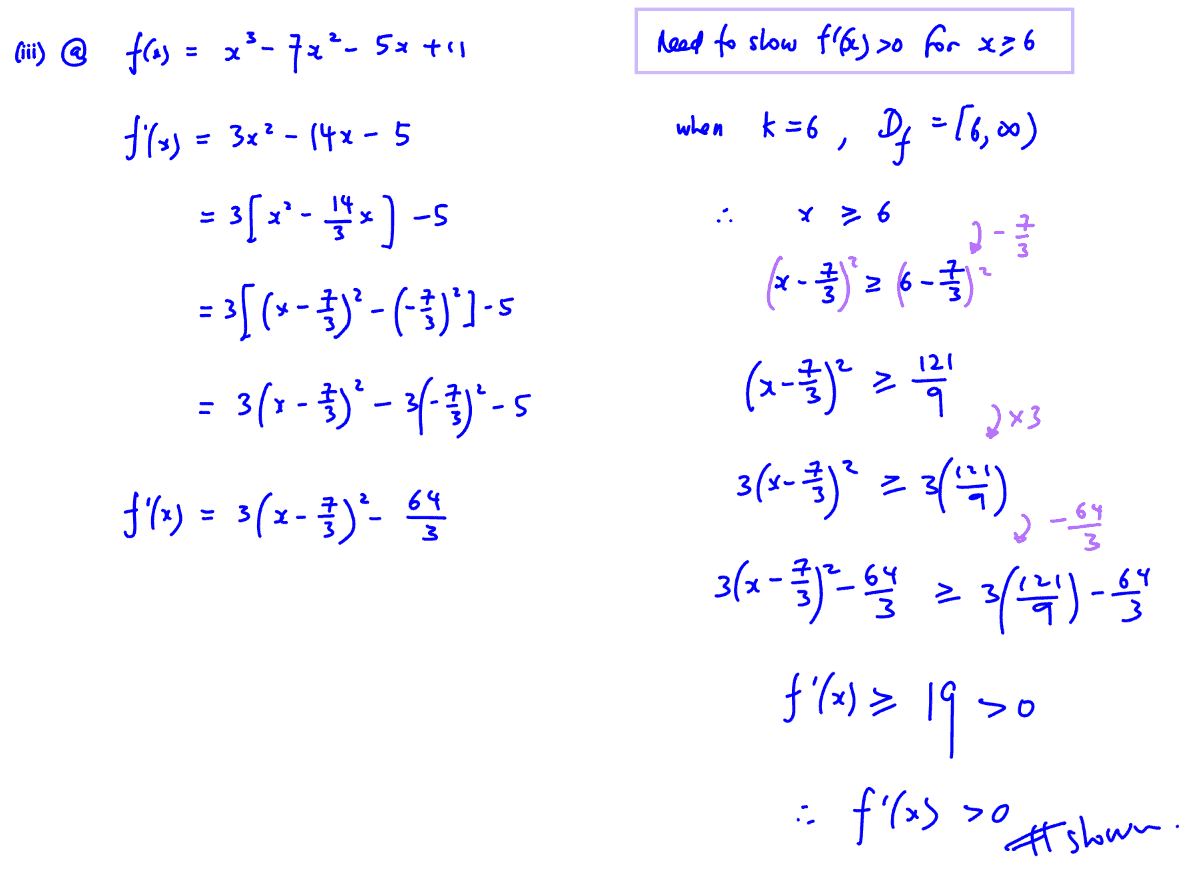
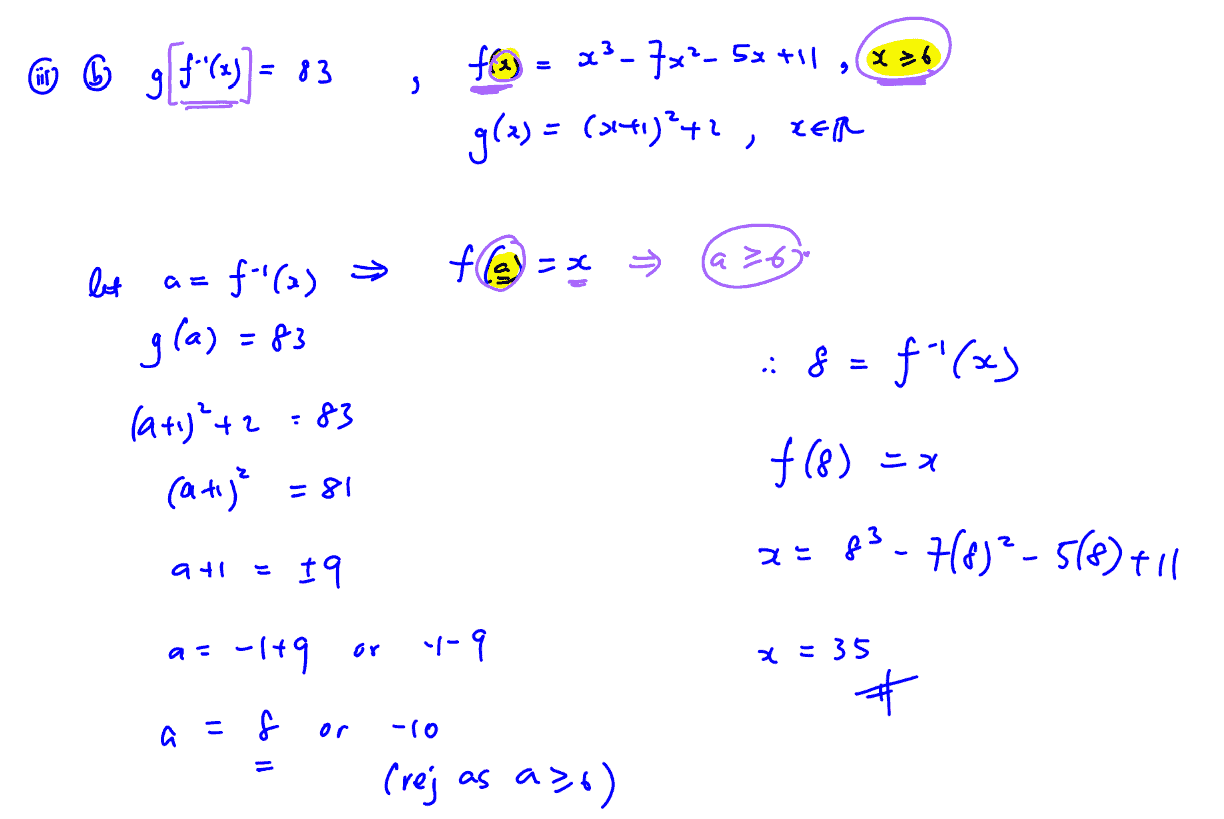
Share with your friends!
2016 ACJC Promo Q8
(i)
$\text{f}:x\mapsto \sin x,$ $x\in \mathbb{R},$ $-\pi \le x\le \pi $ ${{\text{f}}^{-1}}:x\mapsto {{\sin }^{-1}}x,$ $x\in \mathbb{R},$ $-1\le x\le 1$.
With the aid of a sketch, explain what is wrong with the definition of $\text{f}$, and suggest a suitable restriction to its domain such that the definition of ${{\text{f}}^{-1}}$ is correct.[2]
(i) A student defines a function $\text{f}$ and its inverse ${{\text{f}}^{-1}}$ by the following:
$\text{f}:x\mapsto \sin x,$ $x\in \mathbb{R},$ $-\pi \le x\le \pi $
${{\text{f}}^{-1}}:x\mapsto {{\sin }^{-1}}x,$ $x\in \mathbb{R},$ $-1\le x\le 1$.
With the aid of a sketch, explain what is wrong with the definition of $\text{f}$, and suggest a suitable restriction to its domain such that the definition of ${{\text{f}}^{-1}}$ is correct.
[2]
(ii)
[3]
(ii) The function $\text{g}$ is defined by $\text{g}:x\mapsto {{e}^{-{{\left( x+1 \right)}^{2}}}}$, $x\in \mathbb{R}$, $-1\le x\le 0$. Find the inverse function ${{\text{g}}^{-1}}$ in similar form.
[3]
(iii)
[1]
(iii) Explain if the composite function ${{\text{g}}^{-1}}{{\text{f}}^{-1}}$ exists.
[1]
(iv)
[4]
(iv) Write down ${{\text{f}}^{-1}}{{\text{g}}^{-1}}\left( x \right)$and its domain, and find its range. Hence, or otherwise, find the value of $x$ such that $\text{gf}\left( x \right)=\frac{1}{e}$.
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)

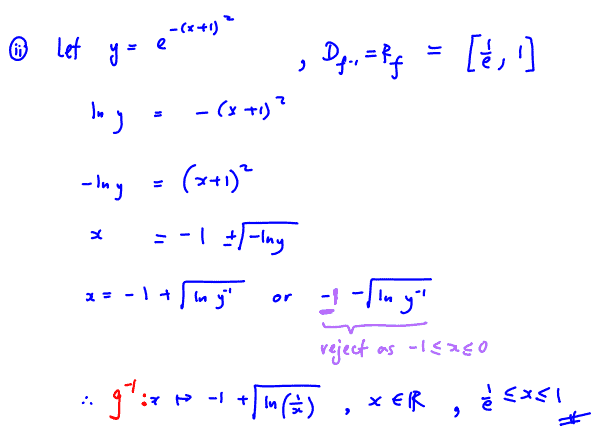
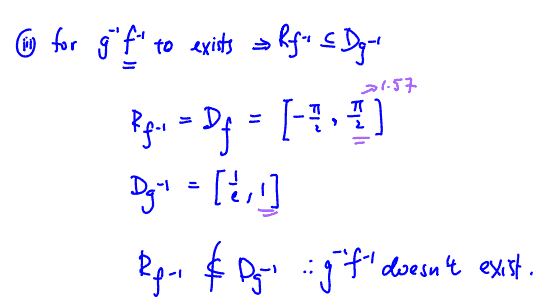
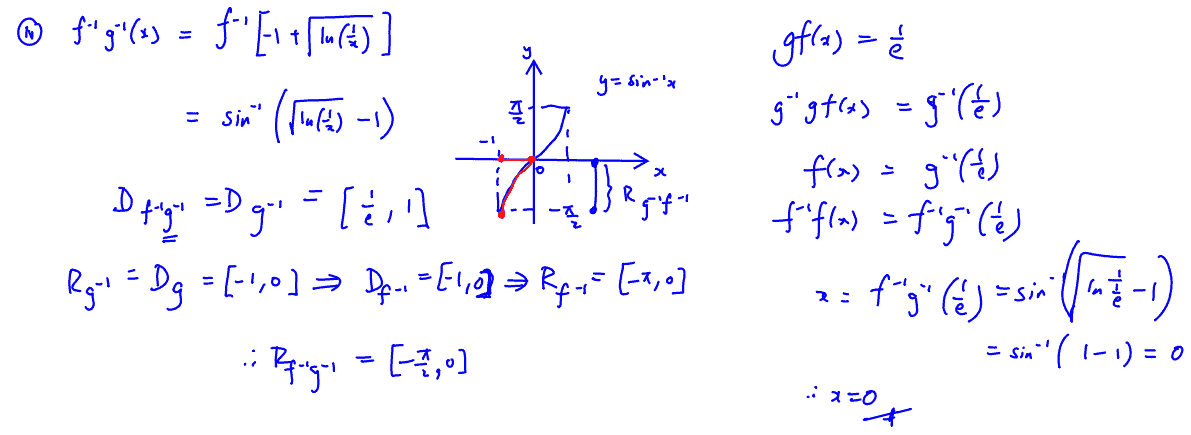
- (i)
- (ii)
- (iii)
- (iv)

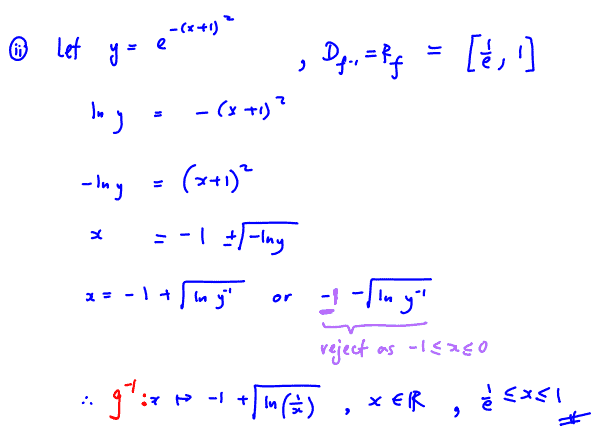
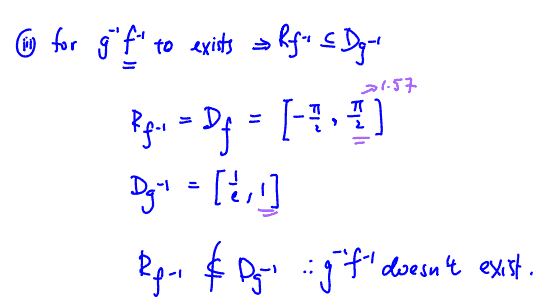
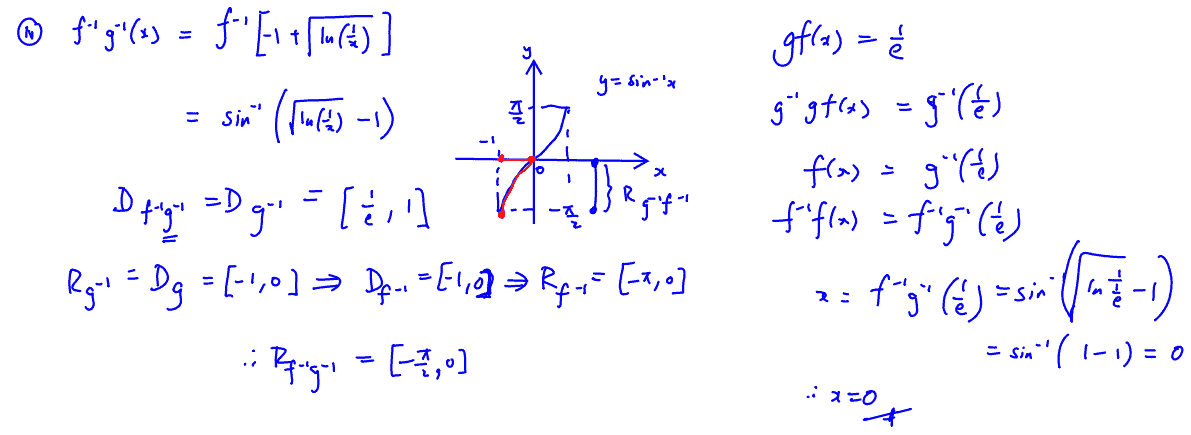
Share with your friends!
Download Functions Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
