A-Level H2 Math | 5 Essential Questions
Graphing Techniques
When you have a system of two or more equations that must be solved simultaneously, one way to do it is by graphing the equations on the same coordinate plane. This is often easier than solving the system algebraically and being able to visualize the solution is a big help in understanding it.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
Graphing Techniques Q1: Prelims Revision
The curve $C$ has equation $y=\frac{{{x}^{2}}+ax+b}{x+c}$, where $a$, $b$ and $c$ are constants. The line $x=3$ is an asymptote to $C$ and the range of values that $y$ can take is given by $y\le -2$ or $y\ge 4$. Find the values of $a$, $b$ and $c$.
[4]
Suggested Handwritten and Video Solutions


Share with your friends!
ACJC Tutorial 2 Q8
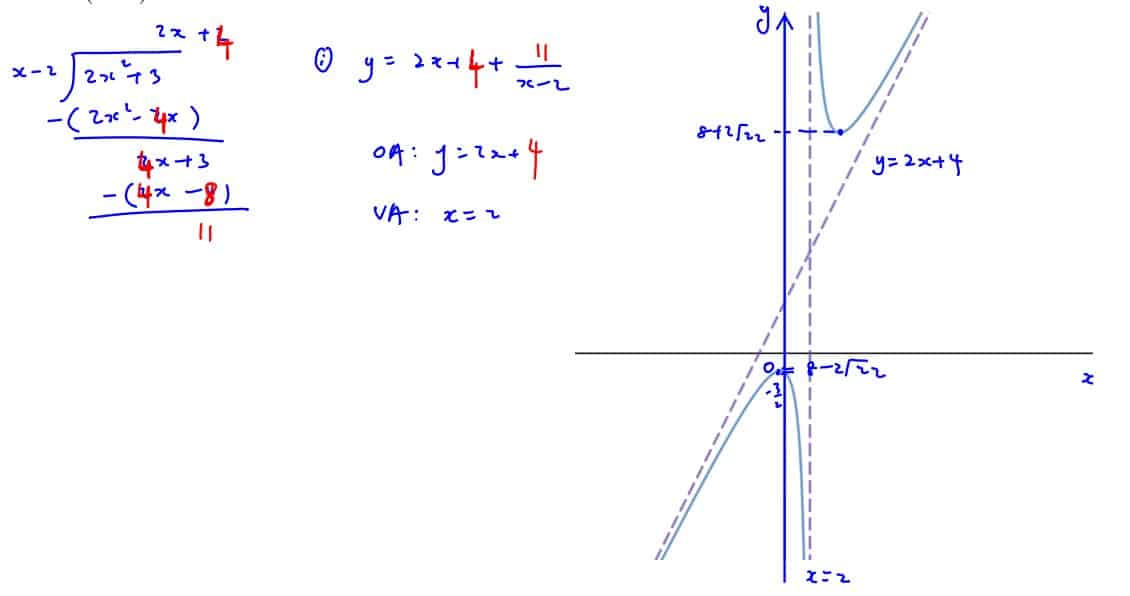
It is given that $y=\frac{2{{x}^{2}}+3}{x-2},x\in \mathbb{R},x\ne 2$.
(i)
Sketch the graph of $y=\frac{2{{x}^{2}}+3}{x-2}$ and label clearly the equations of the asymptotes and intercepts if any.
(i) Sketch the graph of $y=\frac{2{{x}^{2}}+3}{x-2}$ and label clearly the equations of the asymptotes and intercepts if any.
(ii)
The graph of $y=\frac{2{{x}^{2}}+3}{x-2}$ cannot lie between values $p$ and $m$, where $p>m$ . State the value of $p$ and $m$ .
(ii) The graph of $y=\frac{2{{x}^{2}}+3}{x-2}$ cannot lie between values $p$ and $m$, where $p>m$ . State the value of $p$ and $m$ .
(iii)
By means of a graphical argument, state the maximum number of real roots the equation $kx\left( x-2 \right)-2{{x}^{2}}=3$ have.
(iii) By means of a graphical argument, state the maximum number of real roots the equation $kx\left( x-2 \right)-2{{x}^{2}}=3$ have.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)

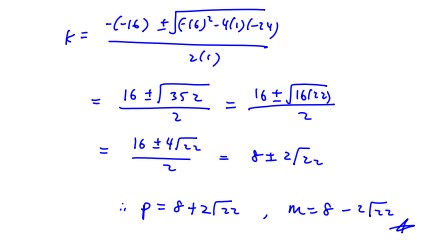

- (i)
- (ii)
- (iii)


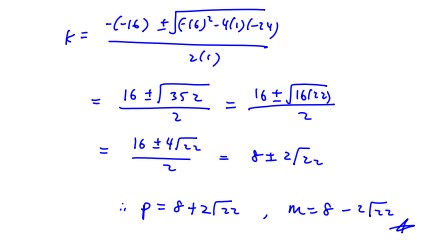

Share with your friends!
2013 YJC P1 Q12
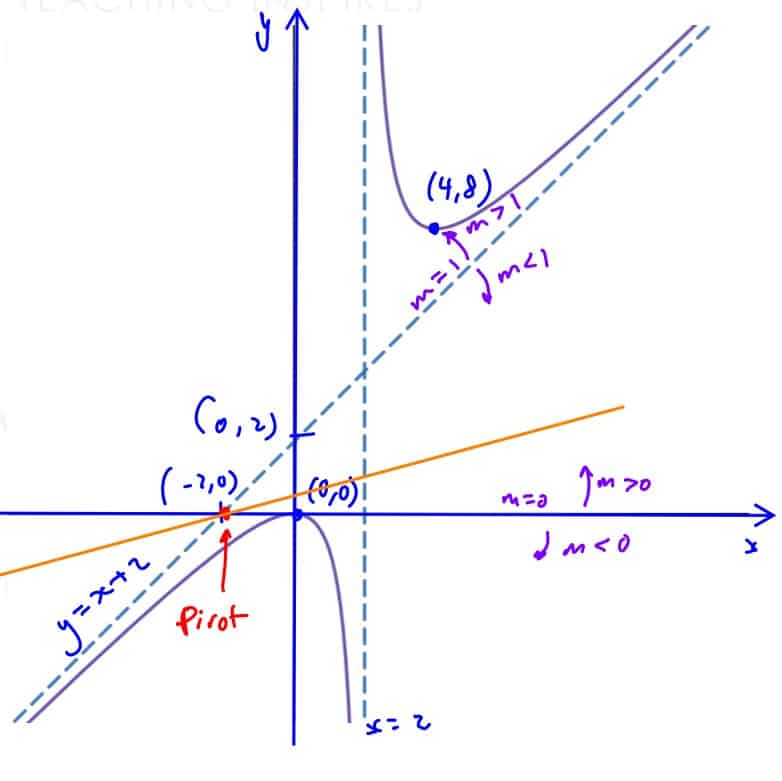
The curve $C$ has equation $y=\frac{{{x}^{2}}}{x-2}$.
(i)
Find the equation(s) of the asymptote(s) of $C$.
[1]
(i) Find the equation(s) of the asymptote(s) of $C$.
[1]
(ii)
Sketch the curve $C$, labelling the equation(s) of its asymptote(s) and coordinates of any axial intercepts and turning points.
[2]
(ii) Sketch the curve $C$, labelling the equation(s) of its asymptote(s) and coordinates of any axial intercepts and turning points.
[2]
(iii)
Hence find the range of values of $k$ for which the equation ${{x}^{2}}=k\left( {{x}^{2}}-4 \right)$ has no real roots.
(iii) Hence find the range of values of $k$ for which the equation ${{x}^{2}}=k\left( {{x}^{2}}-4 \right)$ has no real roots.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
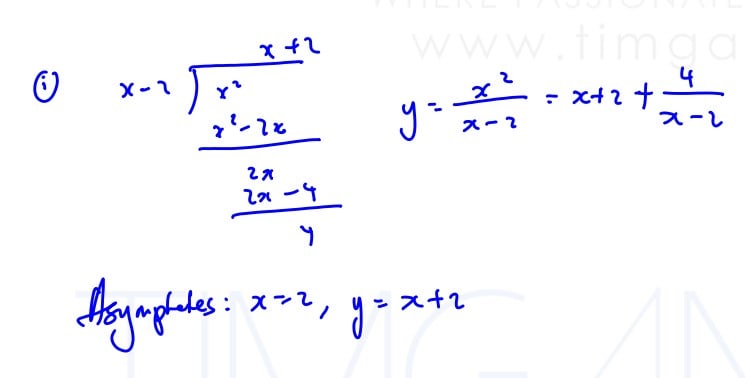
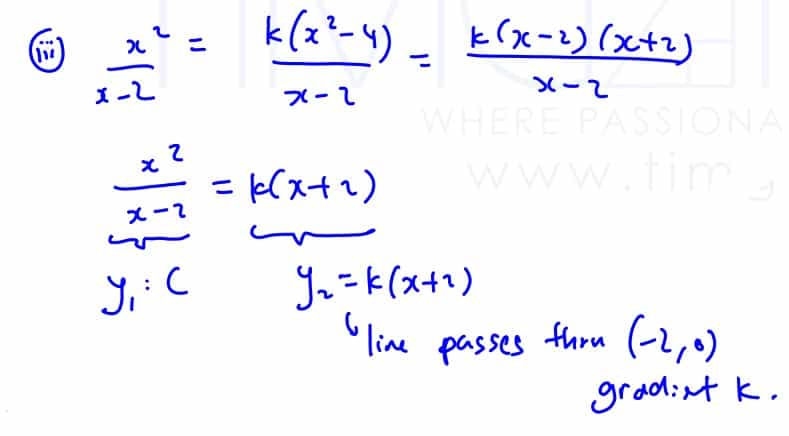
- (i)
- (ii)
- (iii)
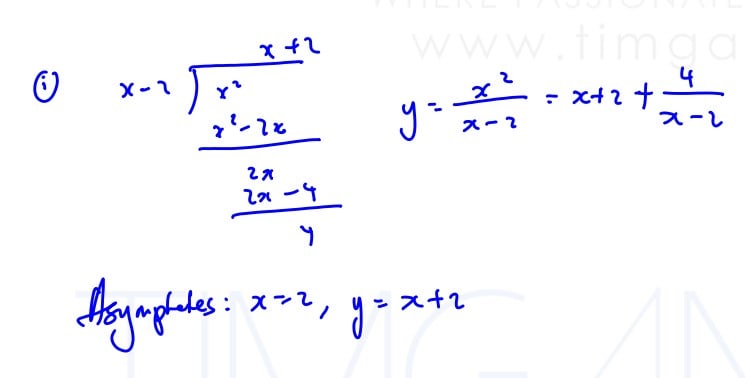

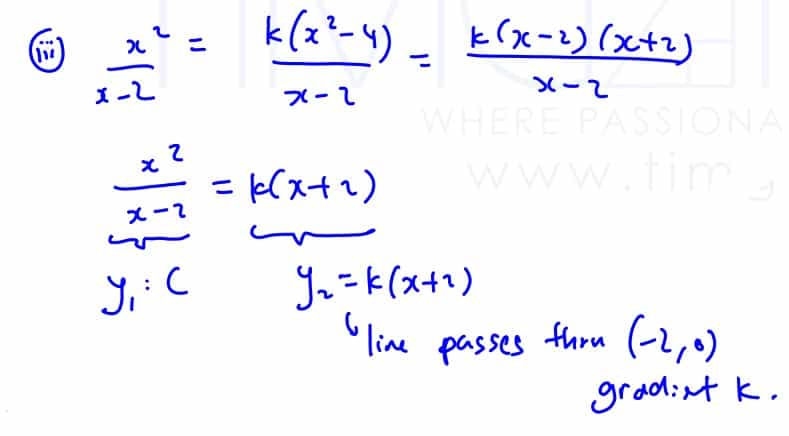
Share with your friends!
2013 MJC Promo Q6
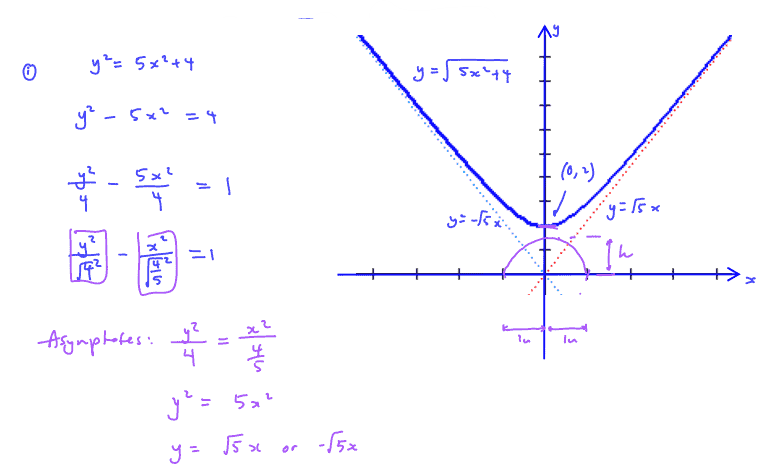
The curve $C$ has equation $y=\sqrt{5{{x}^{2}}+4}$.
(i)
Sketch curve $C$, indicating clearly the axial intercepts, the equations of the asymptotes and the coordinates of the stationary points.
(i) Sketch curve $C$, indicating clearly the axial intercepts, the equations of the asymptotes and the coordinates of the stationary points.
(ii)
Hence, by inserting a suitable graph, determine the range of values of $h$, where $h$ is a positive constant, such that the equation $\sqrt{5{{x}^{2}}+4}=h\sqrt{(1-{{x}^{2}})}$ has no real roots.
(ii) Hence, by inserting a suitable graph, determine the range of values of $h$, where $h$ is a positive constant, such that the equation $\sqrt{5{{x}^{2}}+4}=h\sqrt{(1-{{x}^{2}})}$ has no real roots.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
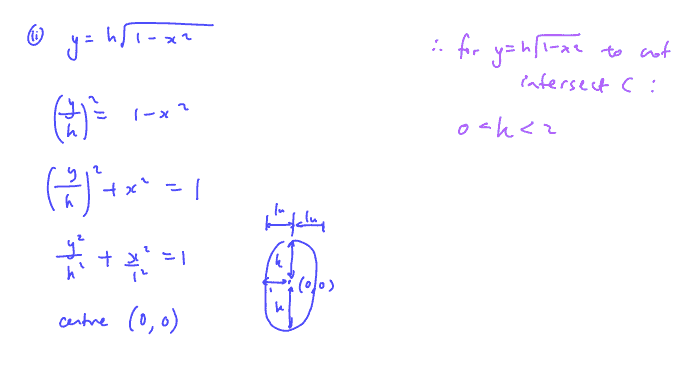
- (i)
- (ii)

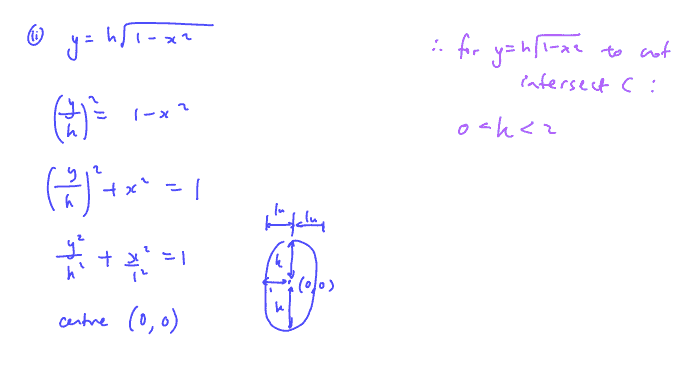
Share with your friends!
2007 SAJC P1 Q7 [Modified]
The curve $C$ has equation $y=\frac{a{{x}^{2}}+2}{x-1}$ where $x\ne 1$ and $a$ is a non-zero constant.
(i)
Show that if the curve $C$ has no stationary points, then $-2<a<0$.
(i) Show that if the curve $C$ has no stationary points, then $-2<a<0$.
(ii)
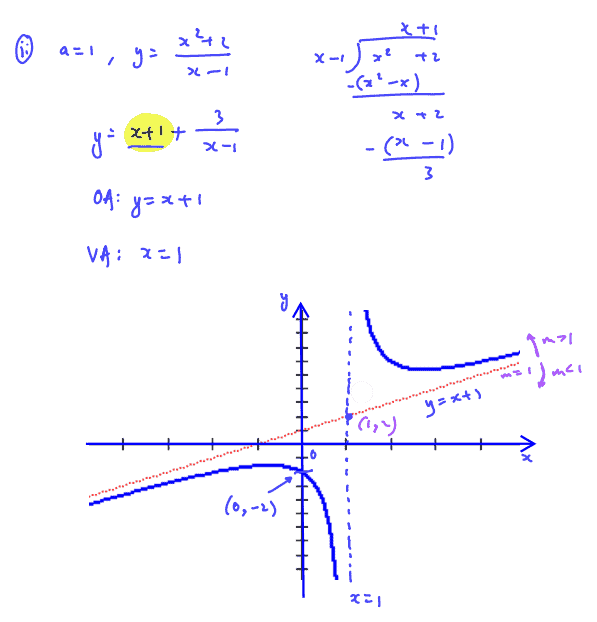
Sketch the curve for $a=1$, showing clearly the asymptotes and coordinates of any intersections with the coordinate axes.
(ii) Sketch the curve for $a=1$, showing clearly the asymptotes and coordinates of any intersections with the coordinate axes.
(iii)
Verify that $y=k(x-1)+2$ passes through $(1,2)$ for all real values of $k$.
(iii) Verify that $y=k(x-1)+2$ passes through $(1,2)$ for all real values of $k$.
(iv)
By considering the equation of an appropriate line drawn on the same diagram with the curve $C$, find the range of values of $k$ for which the equation ${{x}^{2}}+2=k{{(x-1)}^{2}}+2(x-1)$ has no real roots.
(iv) By considering the equation of an appropriate line drawn on the same diagram with the curve $C$, find the range of values of $k$ for which the equation ${{x}^{2}}+2=k{{(x-1)}^{2}}+2(x-1)$ has no real roots.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
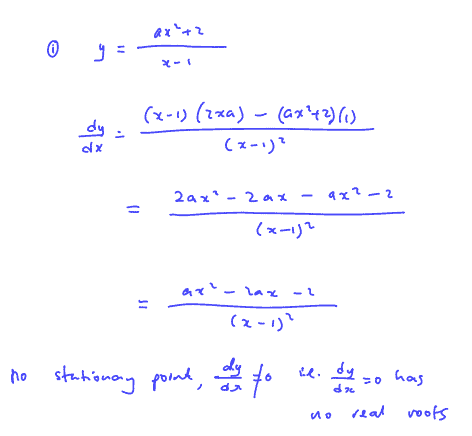
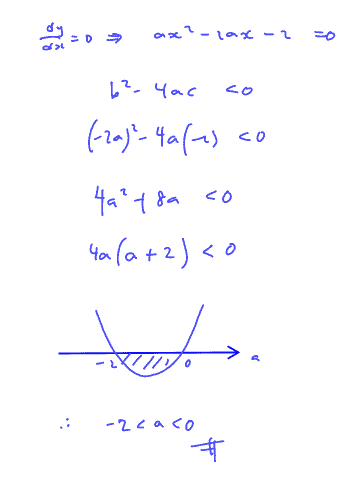
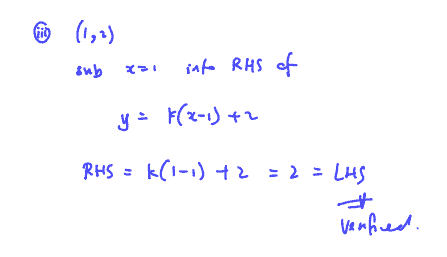
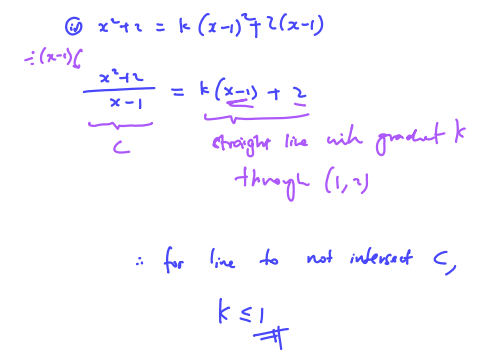
- (i)
- (ii)
- (iii)
- (iv)
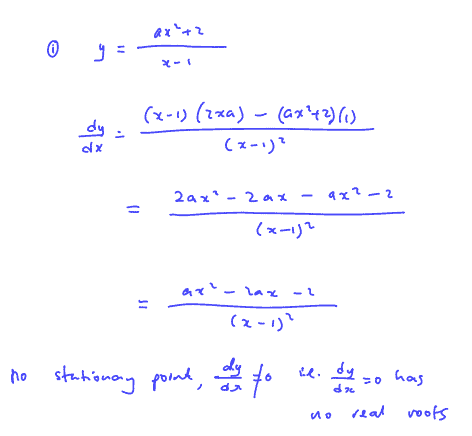
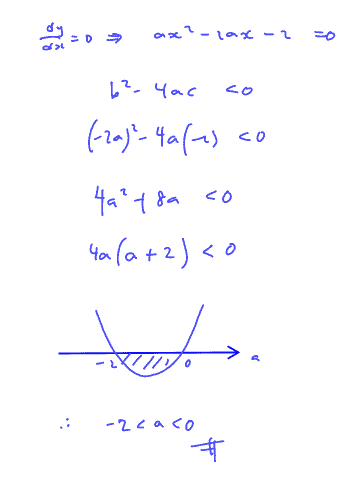

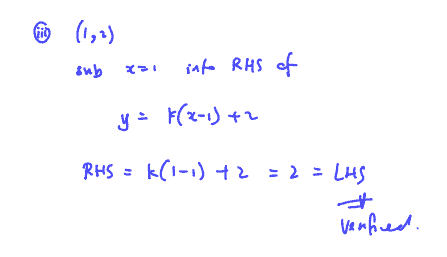
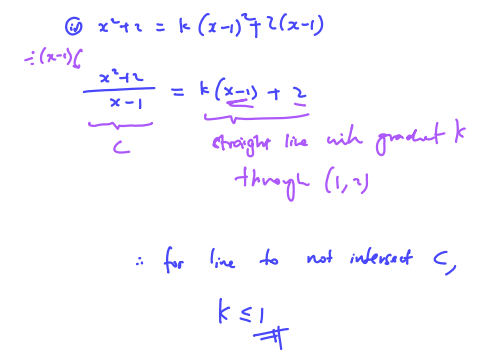
Share with your friends!
Download Graphing Techniques Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
