A-Level H2 Math | 5 Essential Questions
Inequalities
In mathematics, the inequality relation is one of the fundamental building blocks for inequalities. It deals with the mathematical comparison of two elements, and it serves as a key to understanding why numbers behave the way they do. Inequalities allow us to describe sets of numbers and the relationship between those numbers.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each question. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2019 NJC P1 Q2
Without using a calculator
(i)
Solve the inequality $\frac{2{{x}^{2}}+5x+9}{x-7}\le x-4$.
[4]
(i) Solve the inequality $\frac{2{{x}^{2}}+5x+9}{x-7}\le x-4$.
[4]
(ii)
Hence, solve the inequality $\frac{2+5{{e}^{x}}+9{{e}^{2x}}}{7{{e}^{x}}-1}\ge 4{{e}^{x}}-1$.
[2]
(ii) Hence, solve the inequality $\frac{2+5{{e}^{x}}+9{{e}^{2x}}}{7{{e}^{x}}-1}\ge 4{{e}^{x}}-1$.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)



- (i)
- (ii)



Share with your friends!
2013 CJC Promo Q8
(a)
(i)
Without using a calculator, solve the inequality $\frac{x+6}{{{x}^{2}}-3x-4}\le \frac{1}{4-x}$.
[3]
(i) Without using a calculator, solve the inequality $\frac{x+6}{{{x}^{2}}-3x-4}\le \frac{1}{4-x}$.
[3]
(ii)
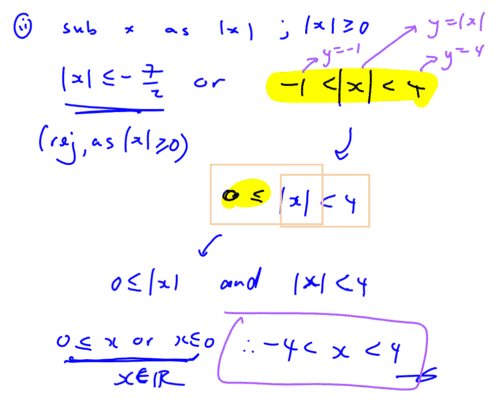
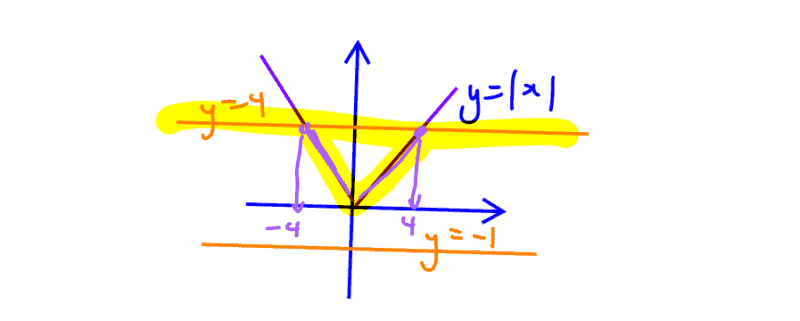
Hence, deduce the range of values of $x$ that satisfies
$\frac{\left| x \right|+6}{{{x}^{2}}-3\left| x \right|-4}\le \frac{1}{4-\left| x \right|}$.
[2]
(ii) Hence, deduce the range of values of $x$ that satisfies
$\frac{\left| x \right|+6}{{{x}^{2}}-3\left| x \right|-4}\le \frac{1}{4-\left| x \right|}$.
[2]
(b)
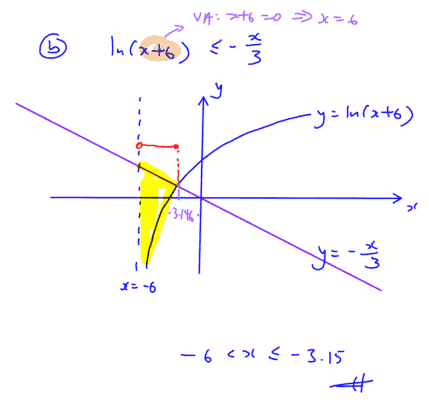
Solve the inequality $\ln \left( x+6 \right)\le -\frac{x}{3}$.
[3]
(b) Solve the inequality $\ln \left( x+6 \right)\le -\frac{x}{3}$.
[3]
Suggested Handwritten and Video Solutions
- (a) (i)
- (a)(ii)
- (b)
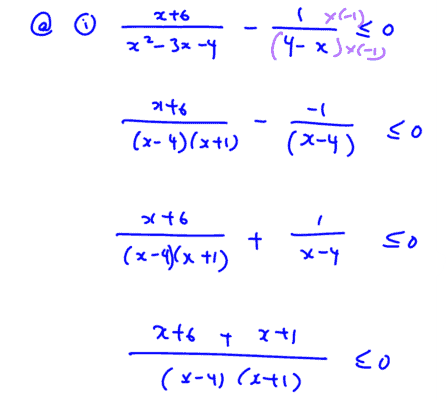
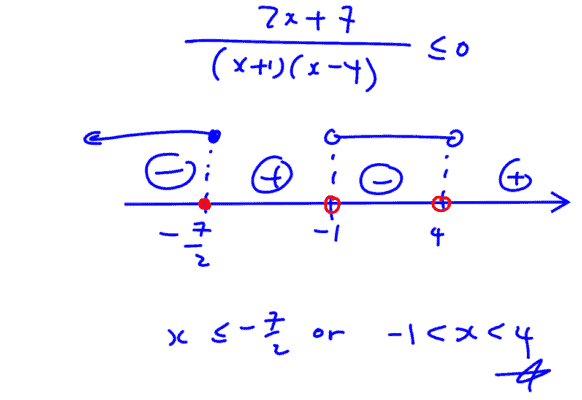
- (a) (i)
- (a) (ii)
- (b)
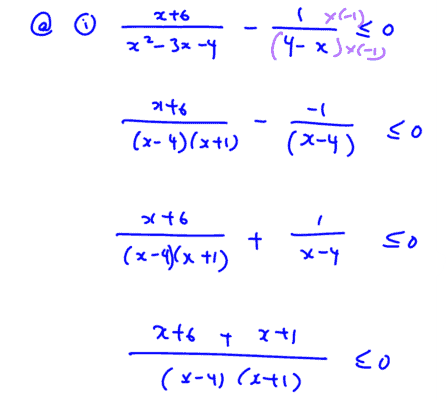
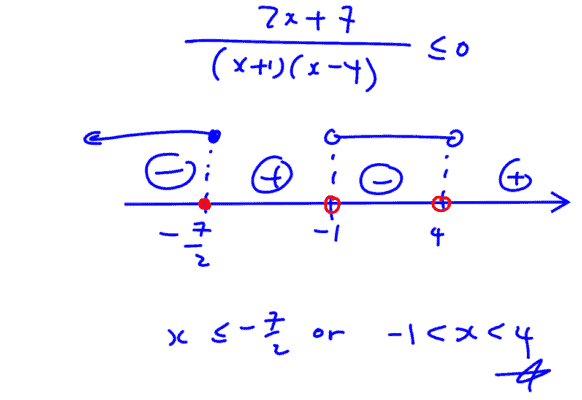



Share with your friends!
2020 CJC Promo Q1
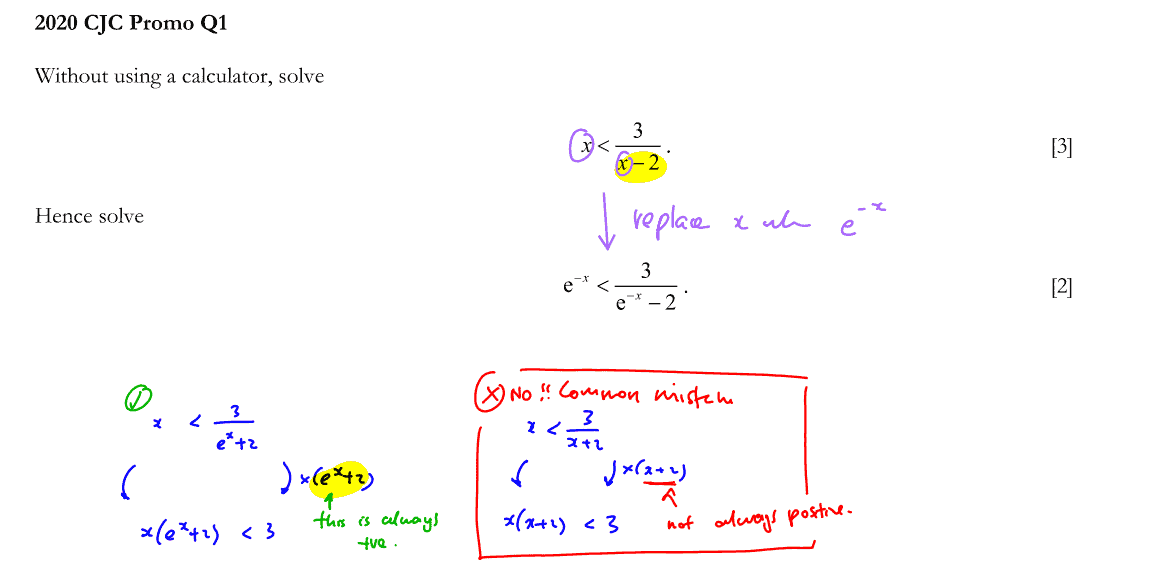
Without using a calculator, solve
$x<\frac{3}{x-2}$.
[3]
Hence solve
${{\text{e}}^{-x}}<\frac{3}{{{\text{e}}^{-x}}-2}$.
[2]
Suggested Handwritten and Video Solutions
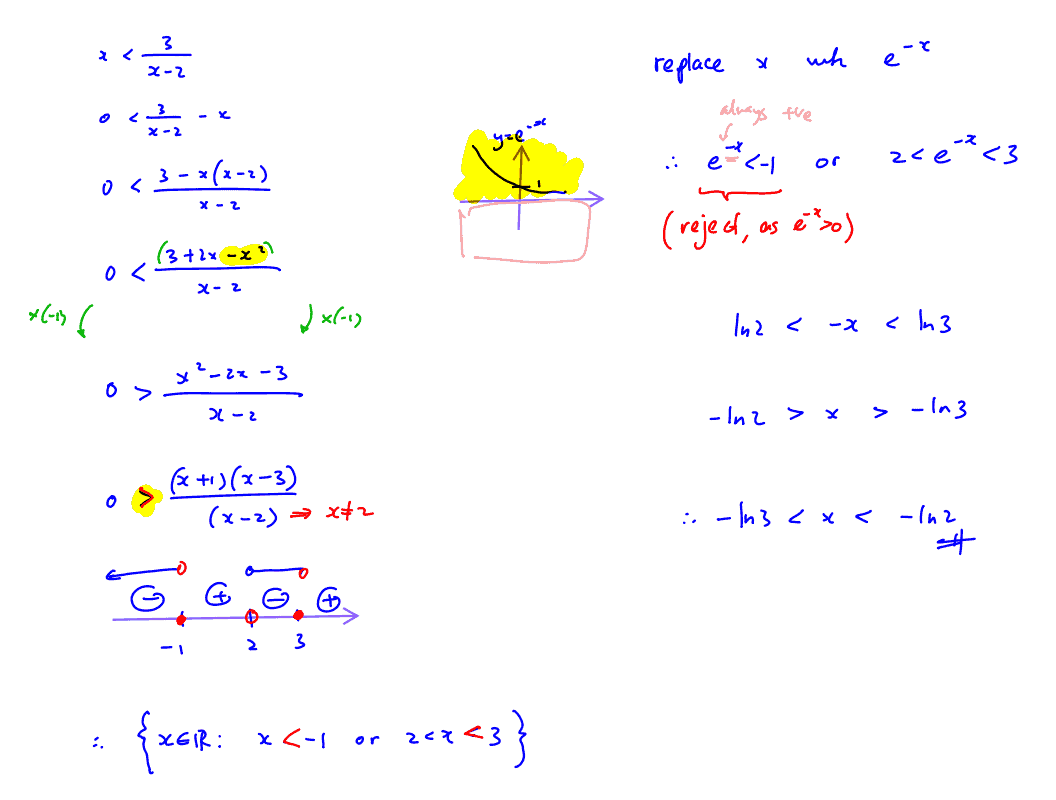
Share with your friends!
2019 TJC Promo Q1
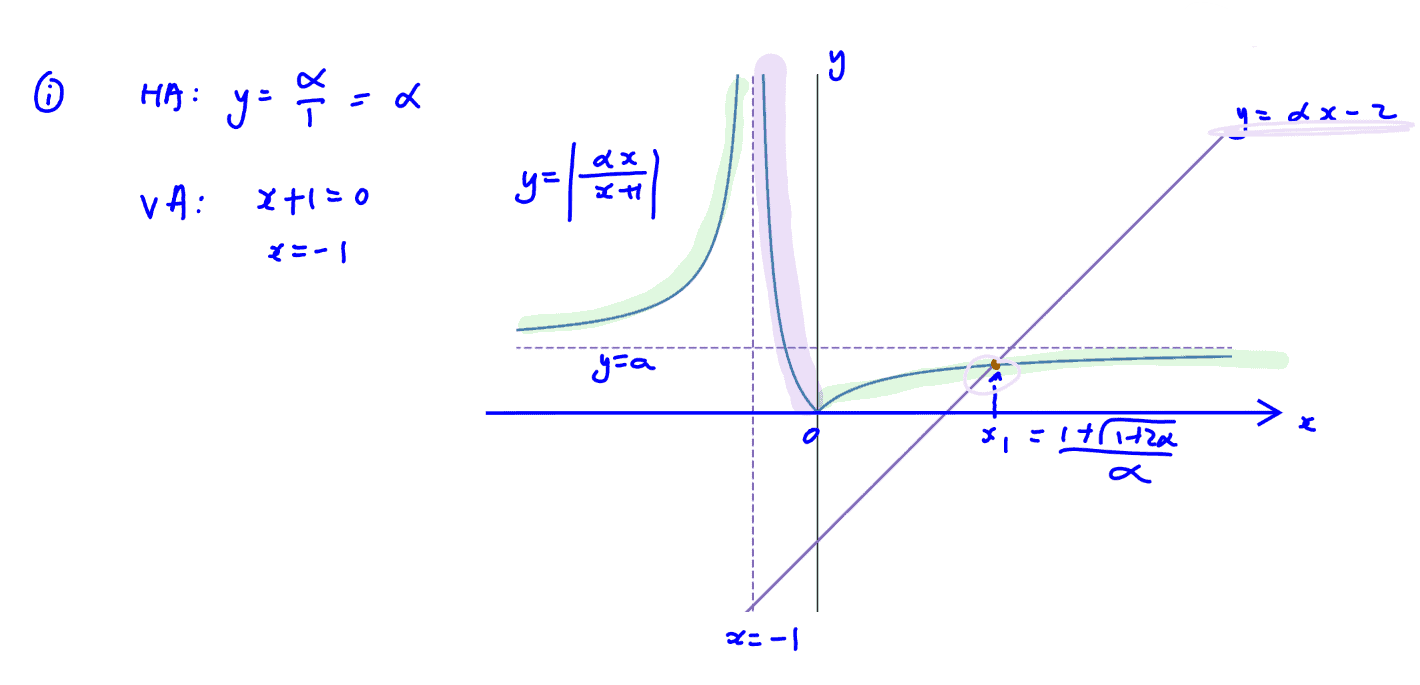
(i)
Sketch the curve with equation $y=\left| \frac{\alpha x}{x+1} \right|$, where $\alpha $ is a positive constant, stating the equations of the asymptotes. On the same diagram, sketch the line with equation $y=\alpha x-2$.
[3]
(i) Sketch the curve with equation $y=\left| \frac{\alpha x}{x+1} \right|$, where $\alpha $ is a positive constant, stating the equations of the asymptotes. On the same diagram, sketch the line with equation $y=\alpha x-2$.
[3]
(ii)
Solve the inequality $\left| \frac{\alpha x}{x+1} \right|\ge \alpha x-2$, giving your answers in term of $\alpha $.
[3]
(ii) Solve the inequality $\left| \frac{\alpha x}{x+1} \right|\ge \alpha x-2$, giving your answers in term of $\alpha $.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- -
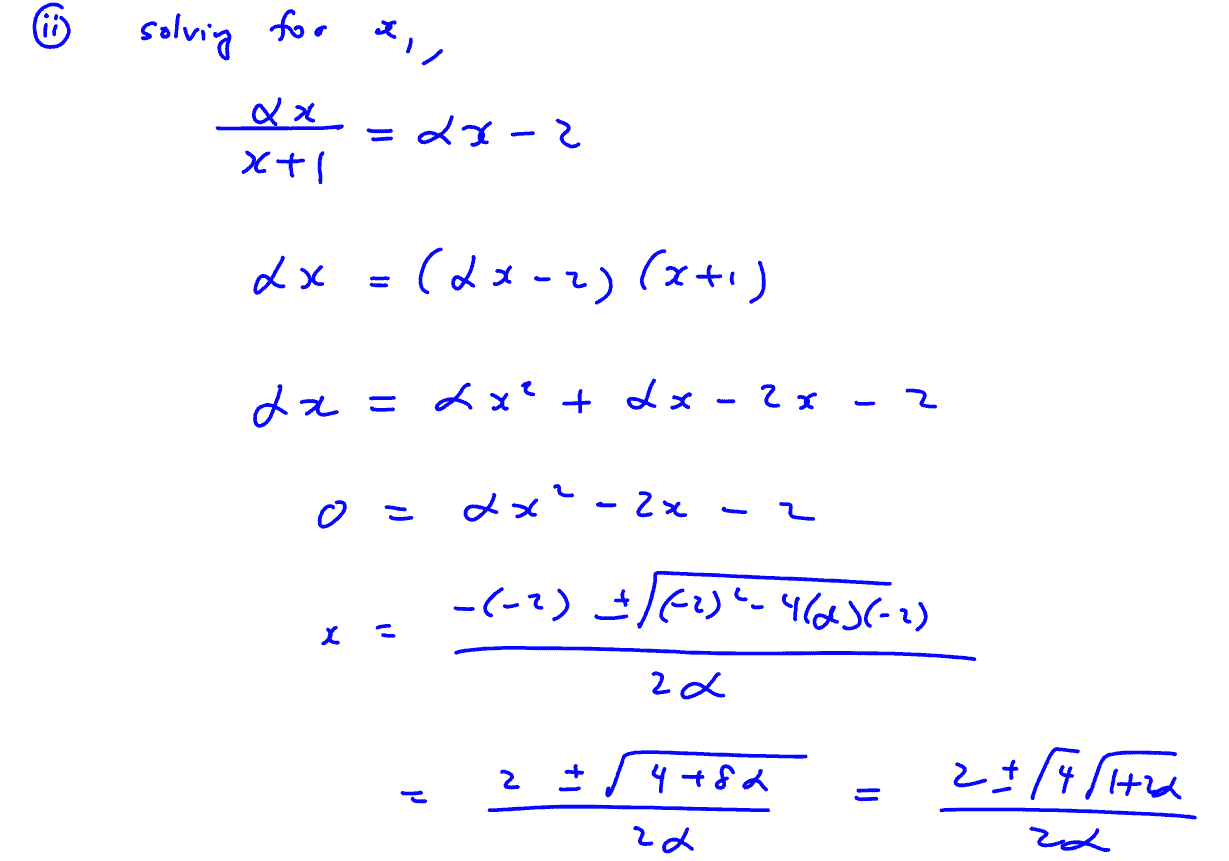
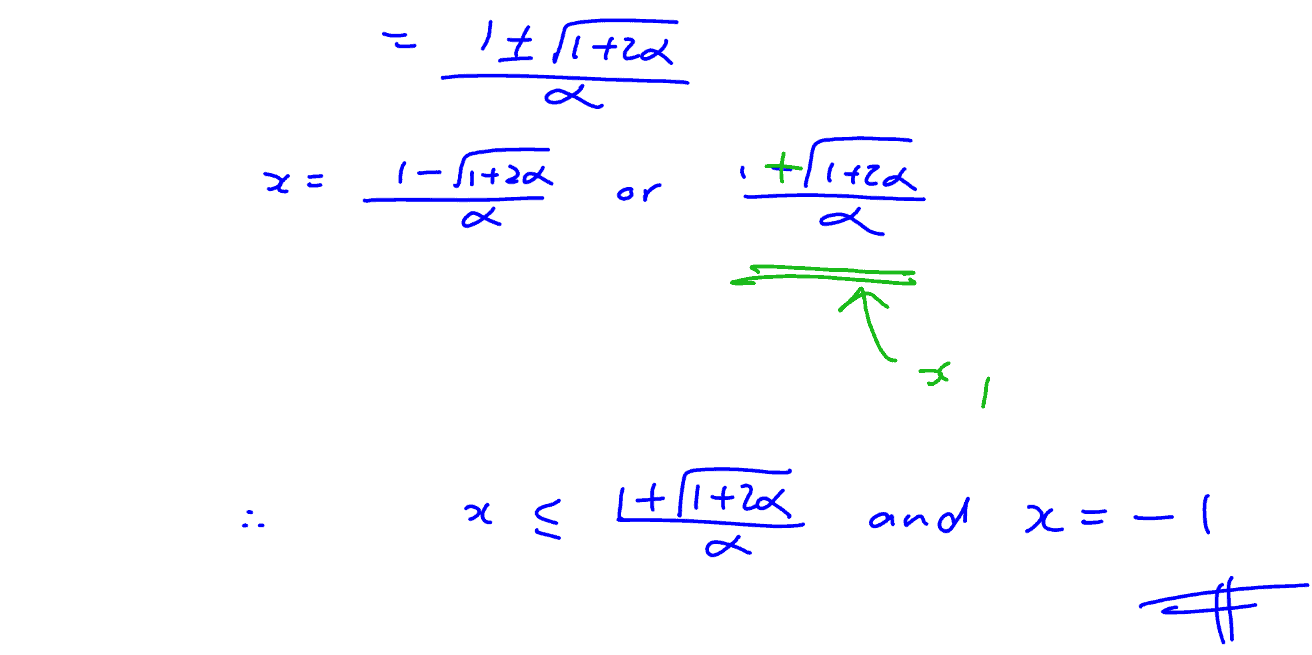
- (i)
- (ii)
- -

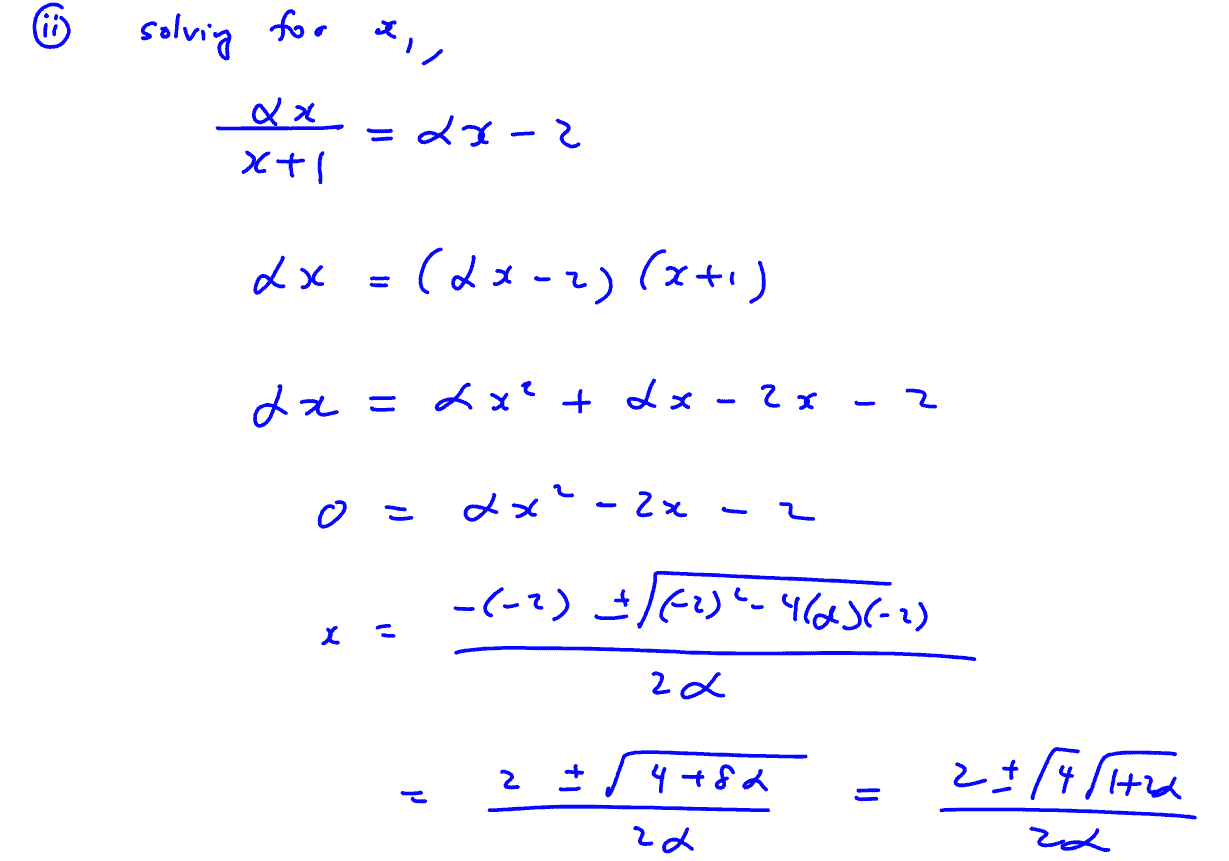
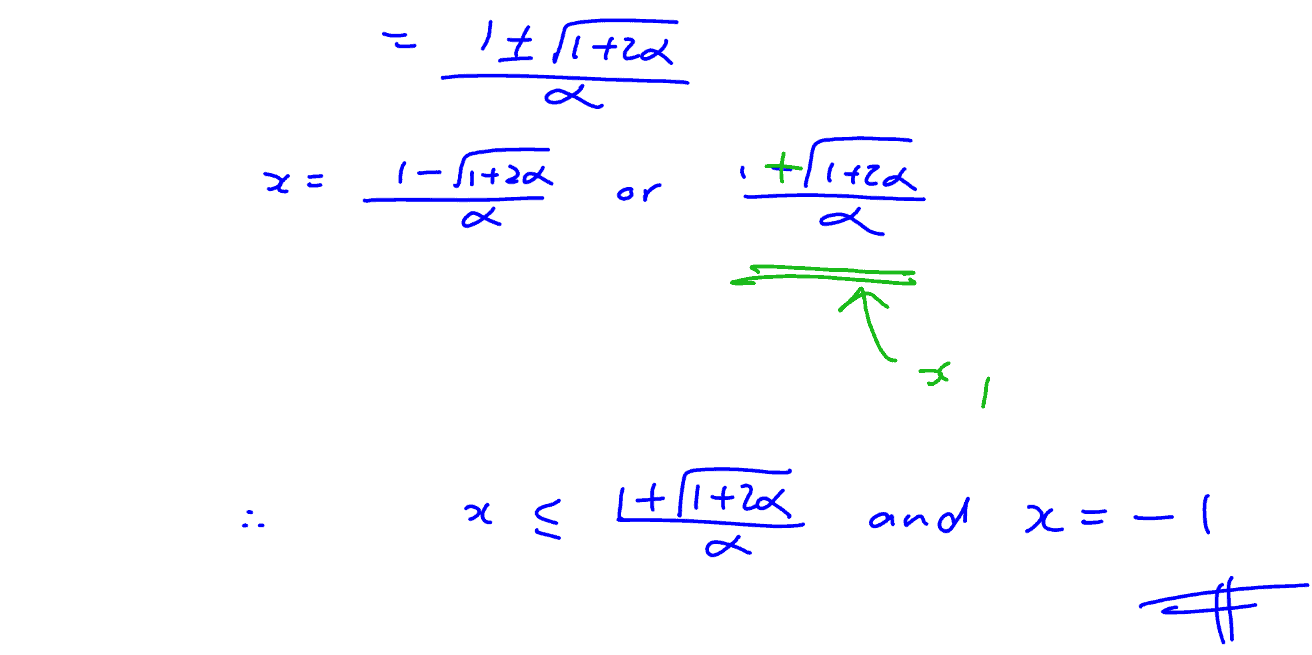
Share with your friends!
2013 ACJC P1 Q1
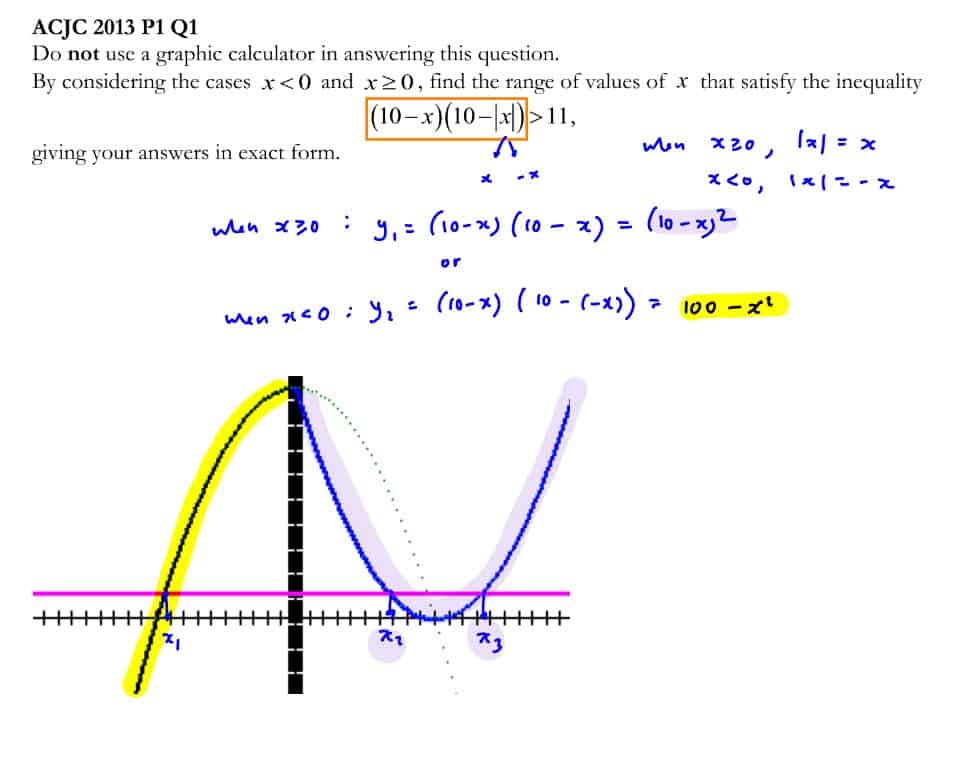
Do not use a graphic calculator in answering this question.
By considering the cases $x<0$ and $x\ge 0$, find the range of values of $x$ that satisfy the inequality
$\left( 10-x \right)\left( 10-\left| x \right| \right)>11$,
giving your answers in exact form.
[5]
Suggested Handwritten and Video Solutions

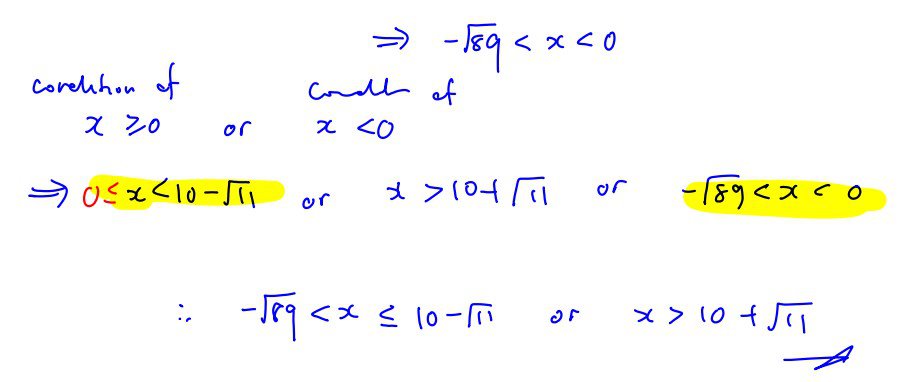
Share with your friends!
Download Inequalities Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
