A-Level H2 Math | 5 Essential Questions
Normal Distribution
The normal distribution is a continuous probability distribution that has a bell-shaped density curve. The curve is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean. It is a very common continuous probability distribution and is often used in the natural and social sciences to represent real-valued random variables whose distributions are not known.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2013 MI P2 Q10
A fruit stall sells $2$ types of durians, XO and D24. For each type of durian, a randomly chosen durian has a mass that is normally distributed with mean and standard deviation, as well as unit price as shown in the following table.
(i)
Find the probability that the total mass of $2$ randomly chosen XO durians is more than $3$ times the mass of a randomly chosen D24 durian.
[3]
(i) Find the probability that the total mass of $2$ randomly chosen XO durians is more than $3$ times the mass of a randomly chosen D24 durian.
[3]
(ii)
Find the probability that the price of a randomly chosen XO durian differs from the price of a randomly chosen D24 durian by less than $\$15$.
[4]
(ii) Find the probability that the price of a randomly chosen XO durian differs from the price of a randomly chosen D24 durian by less than $\$15$.
[4]
A sample of $n$ XO durians is randomly chosen. Find the least value of n such that the probability that the mean mass is more than $2.25$ kg exceeds $0.9$.
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- -

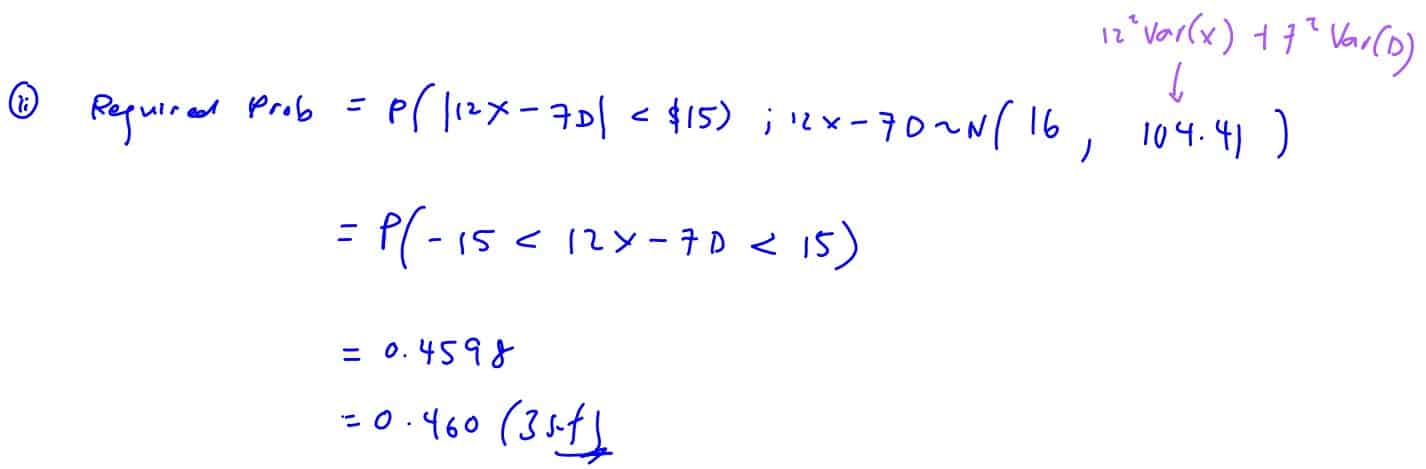
Last Part

- (i)
- (ii)
- -

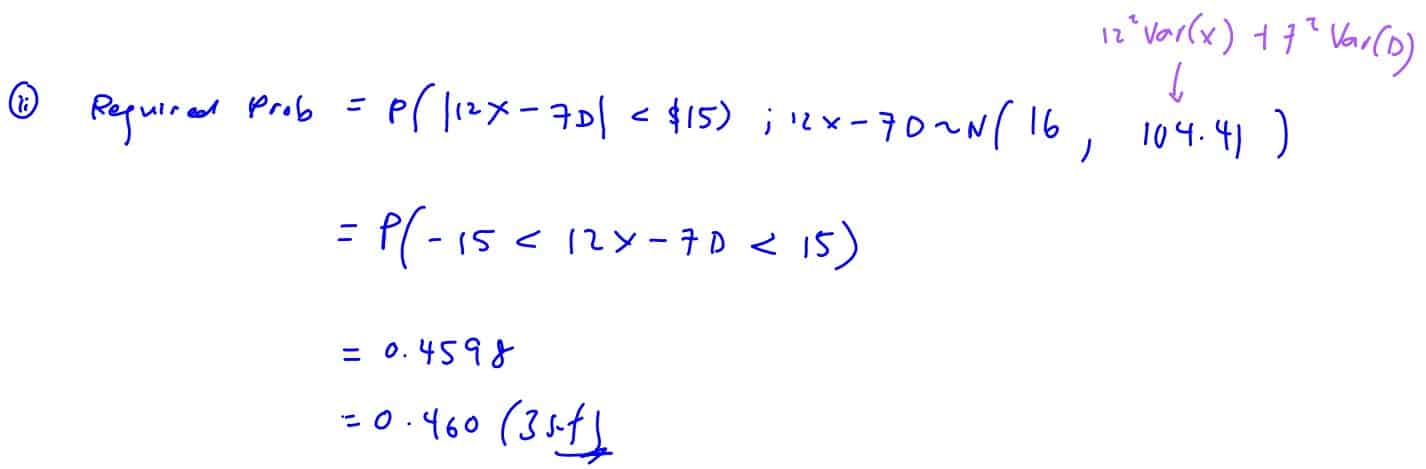
Last Part

Share with your friends!
CJC P2 Q9
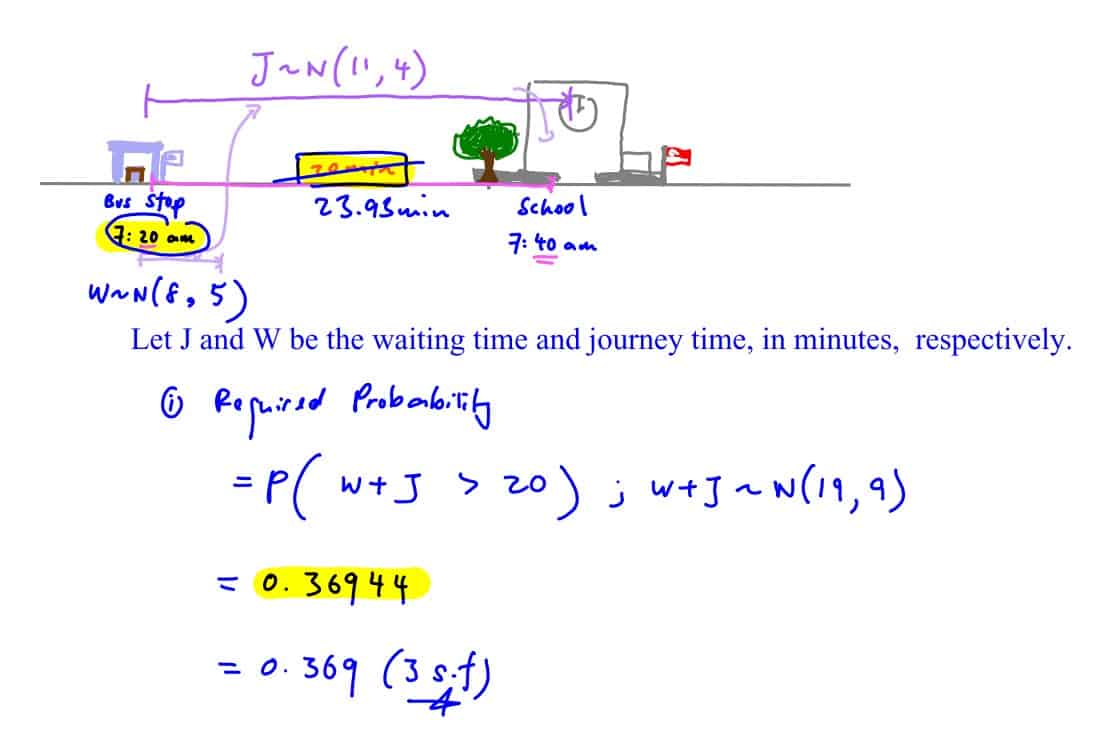
A student reaches the bus-stop outside his house at $7.20$ am every morning to take a bus to school and has to reach his school by $7.40$ am. Assume that the waiting time for his bus is normally distributed with mean 8 minutes and variance $5$ minutes$^{2}$, and the journey time is normally distributed with mean 11 minutes and variance $4$ minutes$^{2}$.
(i)
Find the probability that he will take more than $20$ minutes to reach school (i.e. late for school) on a randomly chosen day.
[2]
(i) Find the probability that he will take more than $20$ minutes to reach school (i.e. late for school) on a randomly chosen day.
[2]
(ii)
In a month of $30$ days, what is the expected number of days he will be late for school?
[1]
(ii) In a month of $30$ days, what is the expected number of days he will be late for school?
[1]
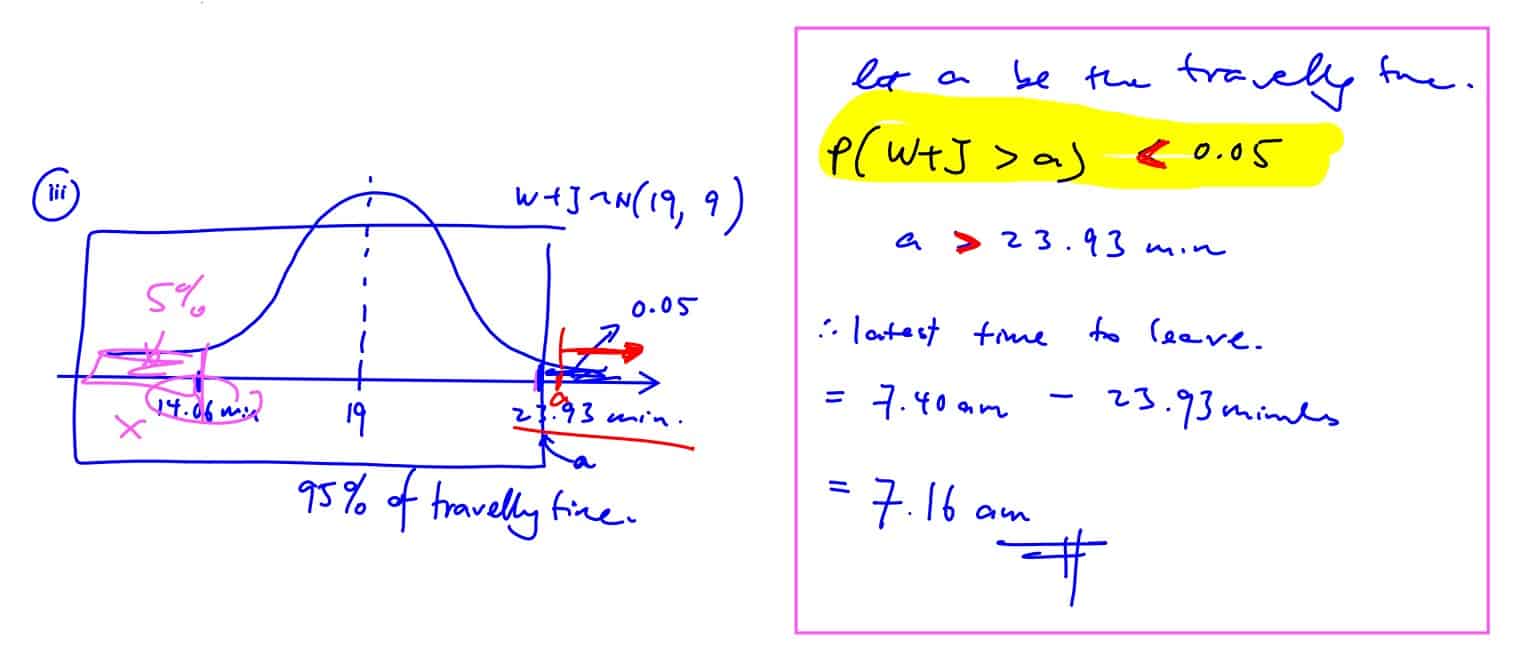
(iii)
Find the latest time he would have to reach the bus-stop outside his house so that the probability of him being late for school is less than $5$%.
[4]
(iii) Find the latest time he would have to reach the bus-stop outside his house so that the probability of him being late for school is less than $5$%.
[4]
(iv)
Find the probability that the average time taken to travel from the bus stop outside his house (including waiting for the bus) to school in 30 days is between $15$ to $20$ minutes.
[2]
(iv) Find the probability that the average time taken to travel from the bus stop outside his house (including waiting for the bus) to school in 30 days is between $15$ to $20$ minutes.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
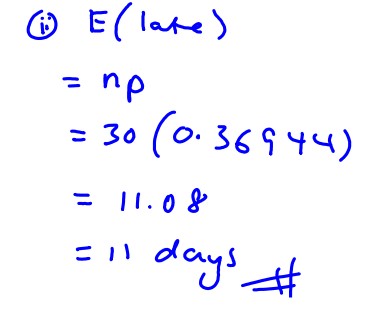
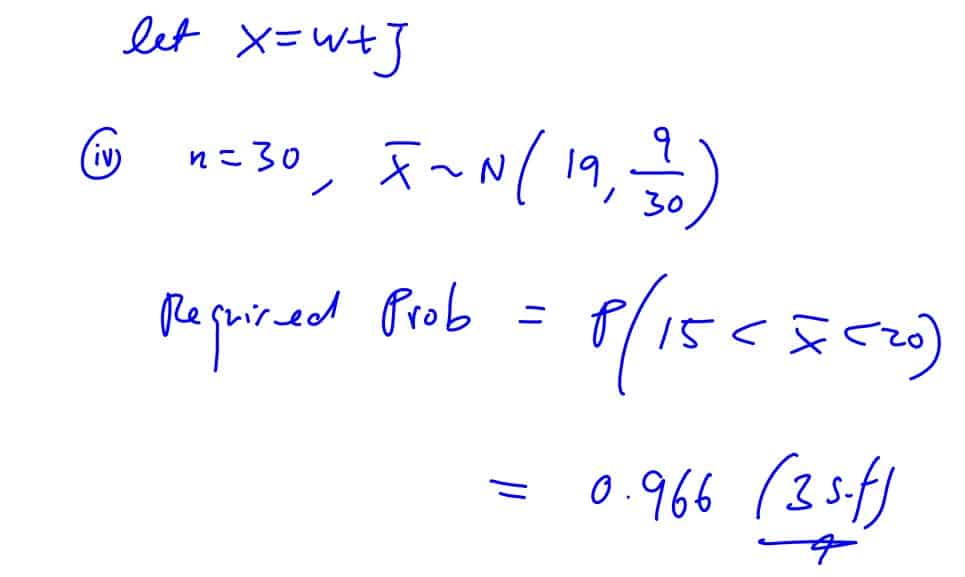
- (i)
- (ii)
- (iii)
- (iv)

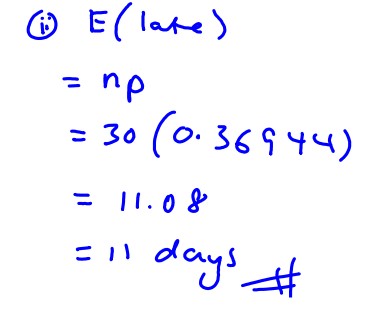

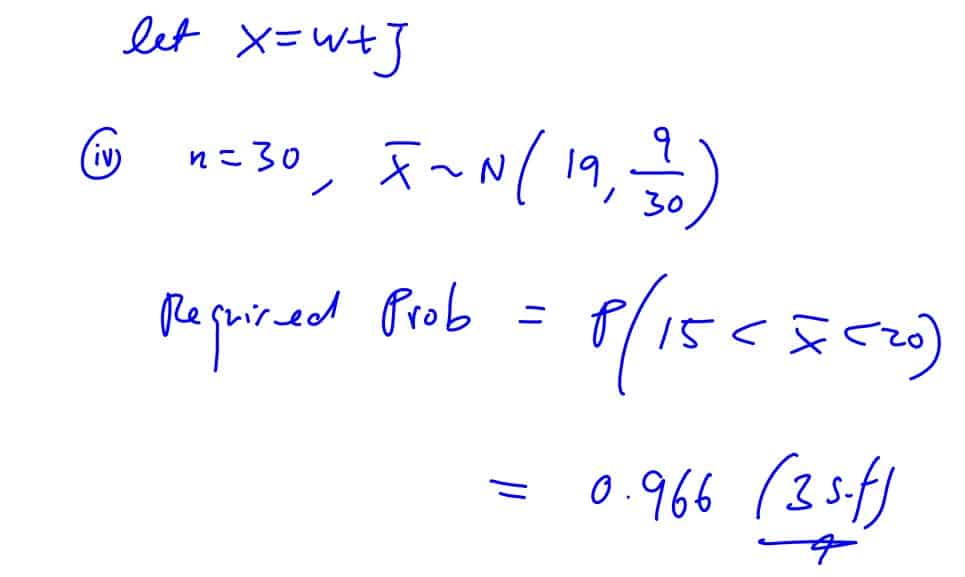
Share with your friends!
2010 PJC P2 Q12
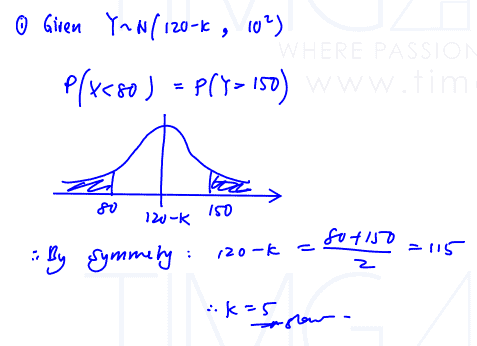
The weight, $Y$, of a Yummy cereal bar is normally distributed with mean $\left( 120-k \right)$g and standard deviation 10g. The weight, F, of a Fullness cereal bar is normally distributed with mean 180 g and standard deviation 20 g.
(i)
Given that $\text{P}\left( Y<80 \right)=\text{P}\left( Y>150 \right)$, show that the value of $k$ is 5.
[1]
(i) Given that $\text{P}\left( Y<80 \right)=\text{P}\left( Y>150 \right)$, show that the value of $k$ is 5.
[1]
(ii)
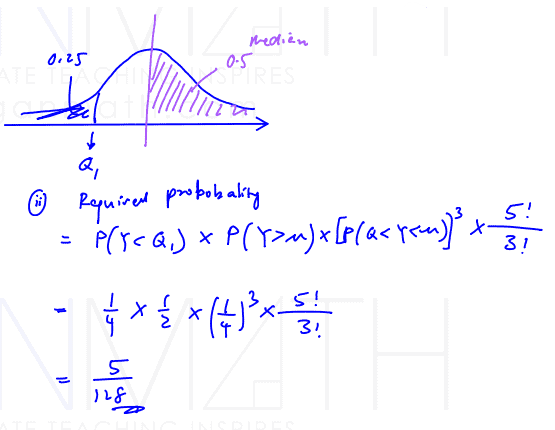
5 Yummy cereal bars are randomly chosen. Find the probability that exactly one bar weighs lesser than the lower quartile weight and exactly one bar weighs more than the median weight.
[2]
(ii) 5 Yummy cereal bars are randomly chosen. Find the probability that exactly one bar weighs lesser than the lower quartile weight and exactly one bar weighs more than the median weight.
[2]
The Fullness cereal bars are sold at $2 per 100g.
(iv)
Find the probability that a randomly chosen Fullness cereal bar costs more than $3.50.
[2]
(iv) Find the probability that a randomly chosen Fullness cereal bar costs more than $3.50.
[2]
(v)
A random sample of 100 Fullness cereal bars is taken. Find the probability that there are at least 55 bars but at most 65 bars with each costing more than $3.50.
[3]
(v) A random sample of 100 Fullness cereal bars is taken. Find the probability that there are at least 55 bars but at most 65 bars with each costing more than $3.50.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
- (v)
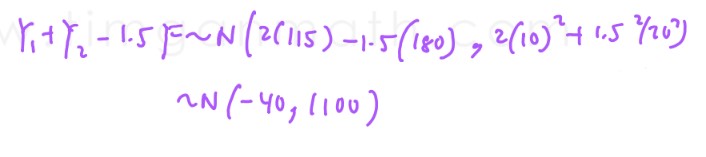


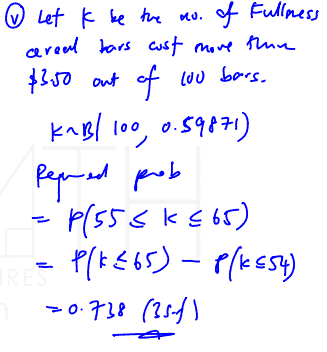
- (i)
- (ii)
- (iii)
- (iv)
- (v)


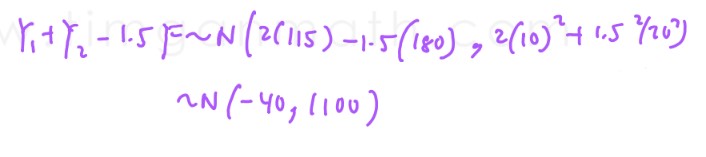


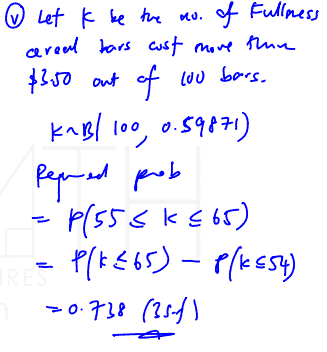
Share with your friends!
2015 VJC P2 Q11
A supermarket sells 2 different types of apples – Granny Smith and Fuji. The masses, in grams, of each type of apples follow normal distributions. The means and standard deviations of these distributions are shown in the following table.

(i)
Two Fuji apples are chosen. Find the probability that their masses differs by at least 20 g.
(i) Two Fuji apples are chosen. Find the probability that their masses differs by at least 20 g.
(ii)
Granny Smith apples are sold at \$3.50 per kg and Fuji apples at \$5 per kg.
(ii) Granny Smith apples are sold at \$3.50 per kg and Fuji apples at \$5 per kg.
Find the probability that six Granny Smith apples and four Fuji apples cost more than $6.50.
(iii)
State an assumption needed for your calculations in parts (i) and (ii).
(iii) State an assumption needed for your calculations in parts (i) and (ii).
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
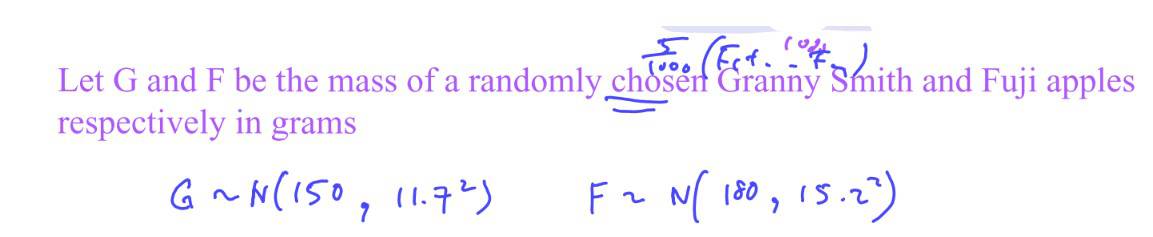
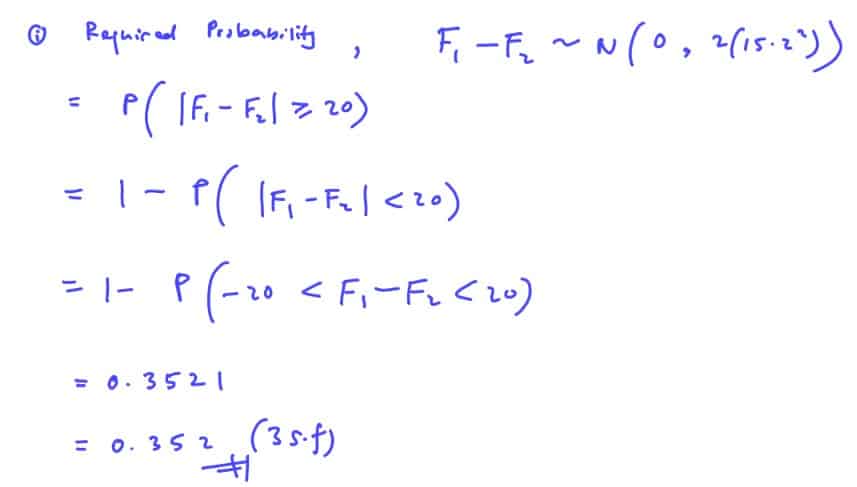
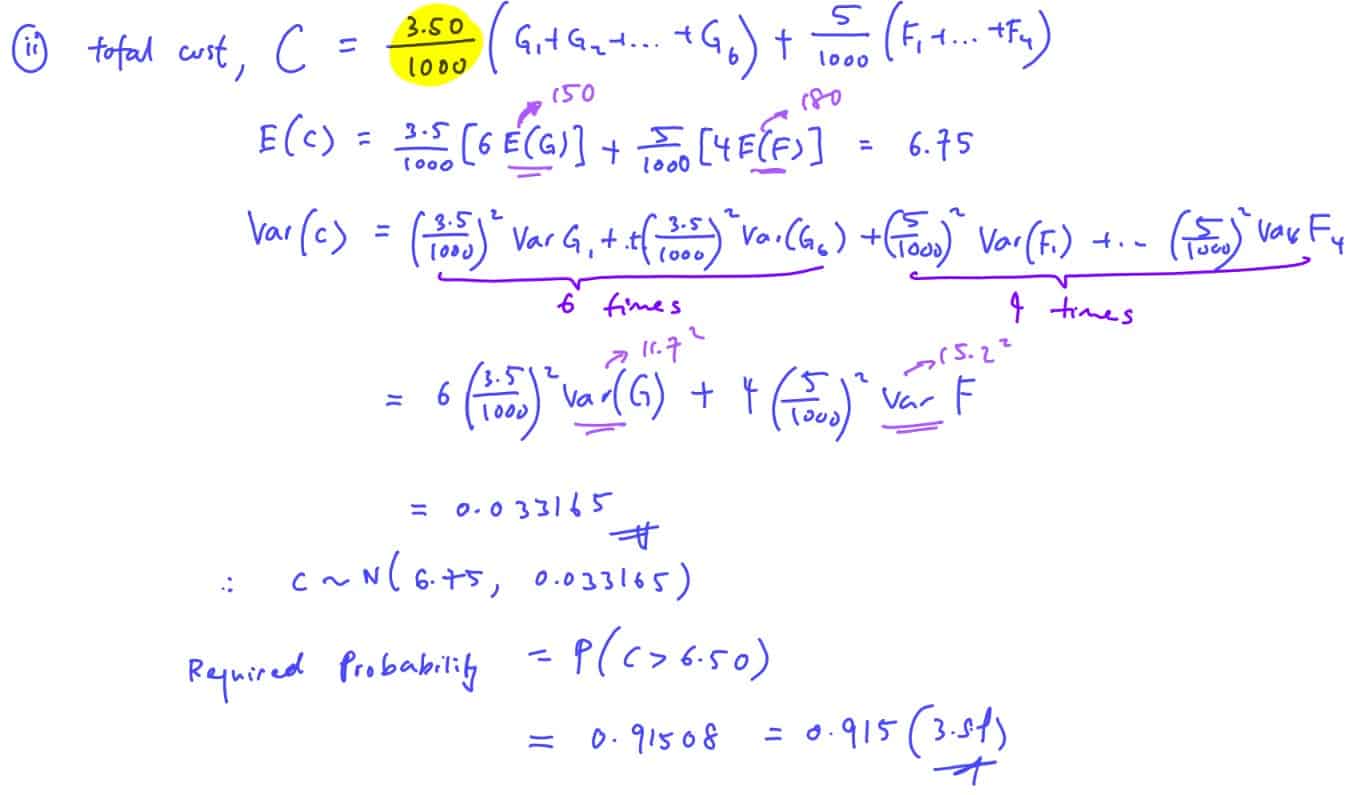

- (i)
- (ii)
- (iii)
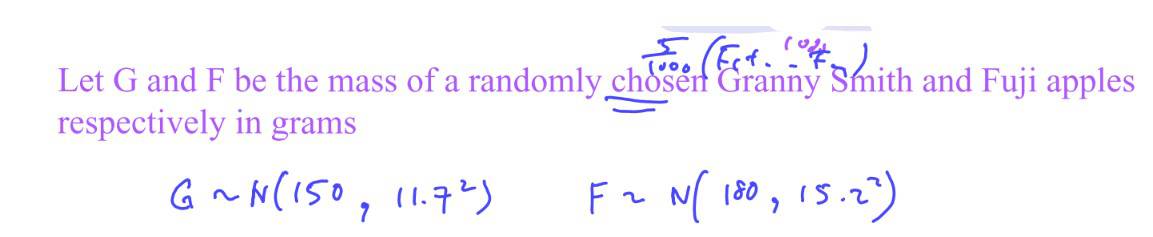
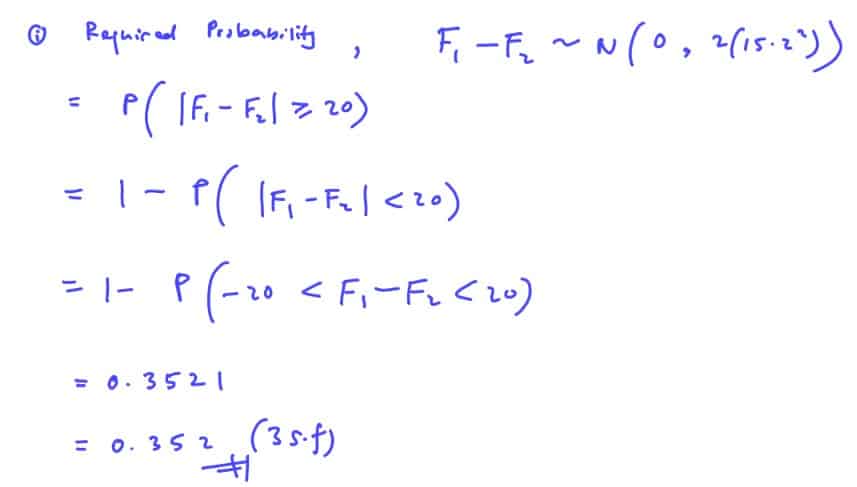
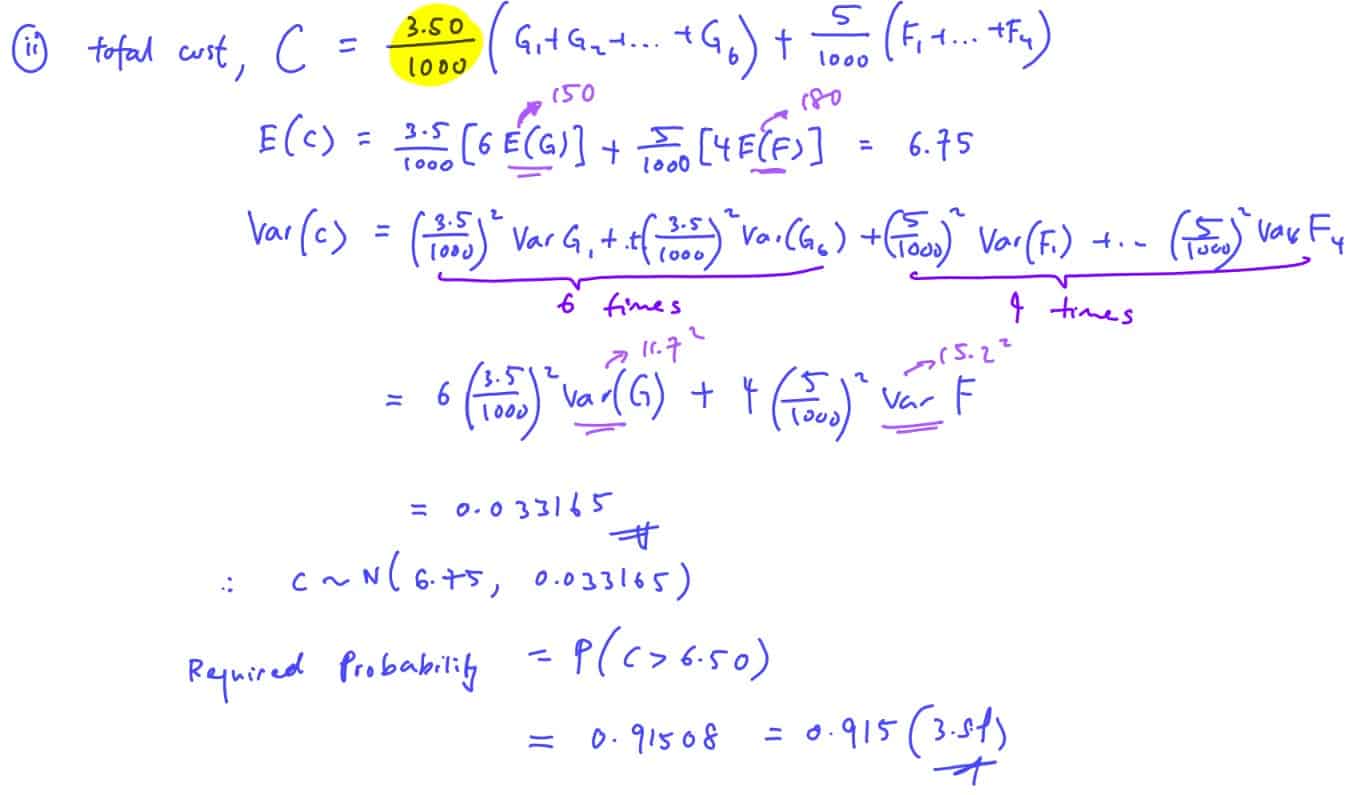

Share with your friends!
2019 ASRJC P2 Q6 (i)
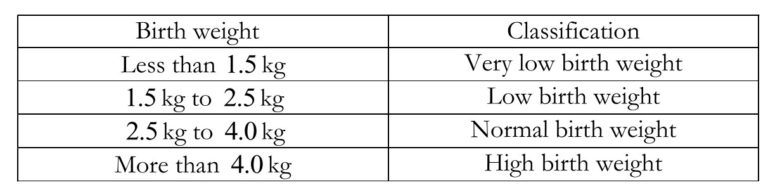
Birth weight can be used to predict short and long-term health complications for babies. Studies show that the birth weight of babies born to mothers who do not smoke in a certain hospital can be assumed to follow a normal distribution with mean $3.05$ kg and variance ${{\sigma }^{2}}$kg$^{2}$.
The hospital classifies babies based on their birth weight as shown as in the table below.
(i)
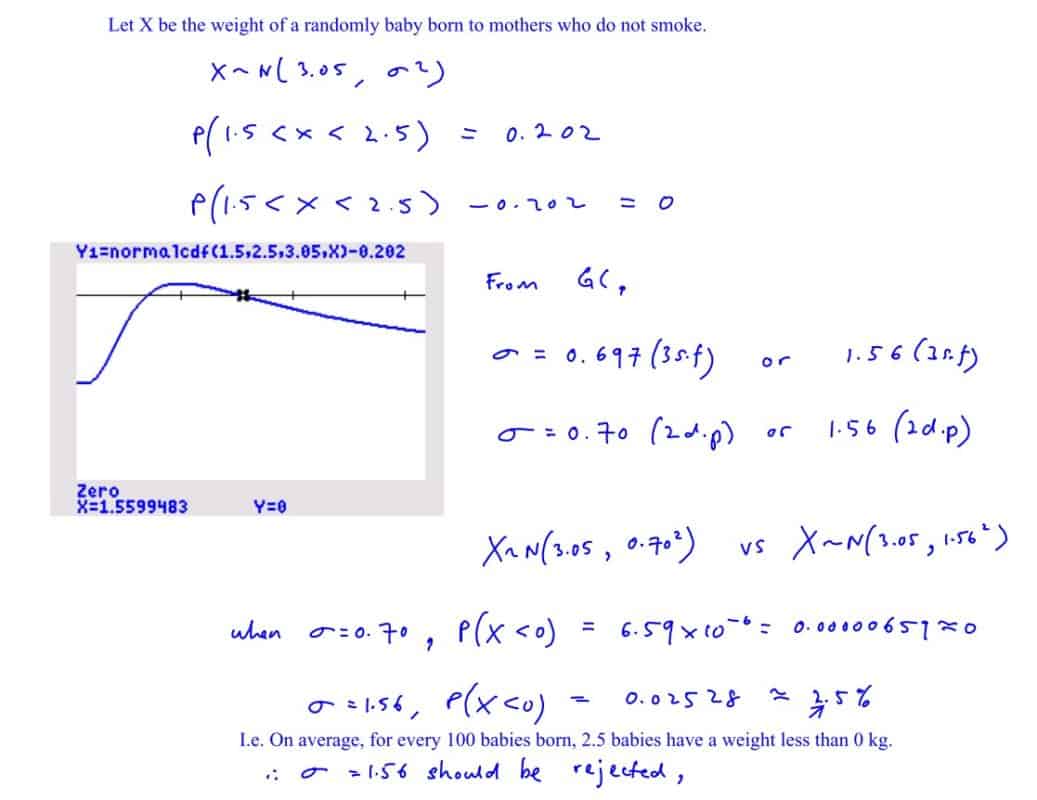
A sample showed that $20.2%$ of the babies born to mothers who do not smoke have low birth weight. If this is true for the entire population, find two possible values of $\sigma $, corrected to $2$ decimal places. Explain clearly why one of the values of $\sigma $ found should be rejected.
[4]
(i)
A sample showed that $20.2%$ of the babies born to mothers who do not smoke have low birth weight. If this is true for the entire population, find two possible values of $\sigma $, corrected to $2$ decimal places. Explain clearly why one of the values of $\sigma $ found should be rejected.
[4]
Suggested Handwritten and Video Solutions
Share with your friends!
Download Normal Distribution Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!

