A-Level H2 Math | 5 Essential Questions
Parametric Equations
Parametric equations are a set of equations that express a set of quantities as explicit functions of a number of independent variables, known as parameters. They are often used to express the coordinates of the points that make up a geometric object such as a curve or surface, in which case the curves are called parametric curves or parametric surfaces.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each question. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
YI Tutorial Question 1
The parametric equations of a curve is given by
$x={{\sin }^{2}}t$, $y=3\cos t$ for $0\le t\le \pi $
(i)
Find the cartesian equation of this curve.
(i) Find the cartesian equation of this curve.
(ii)
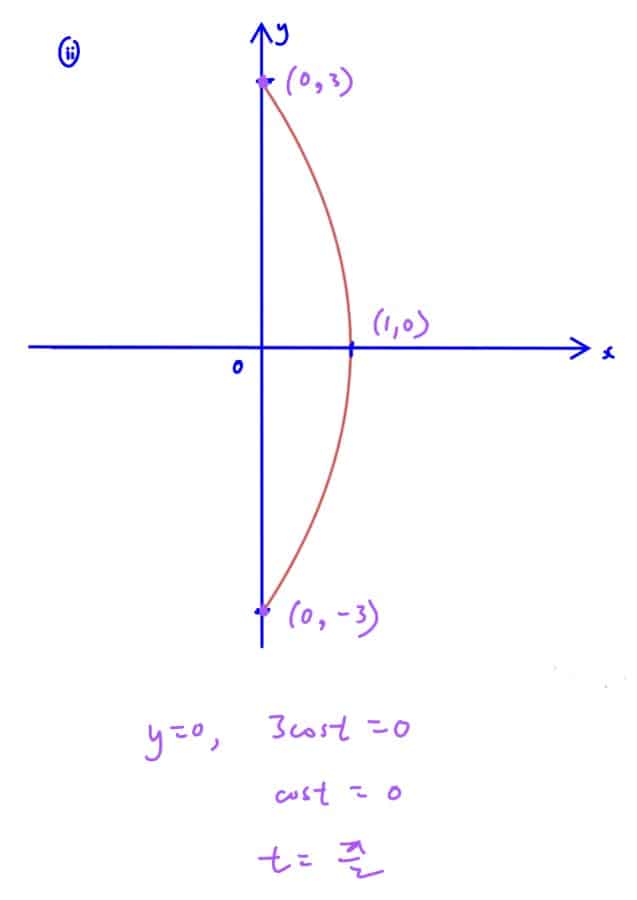
Sketch the curve.
(ii) Sketch the curve.
(iii)
Find the value of $t$ at the point on curve whose tangent is parallel to the $y$-axis.
(iii) Find the value of $t$ at the point on curve whose tangent is parallel to the $y$-axis.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
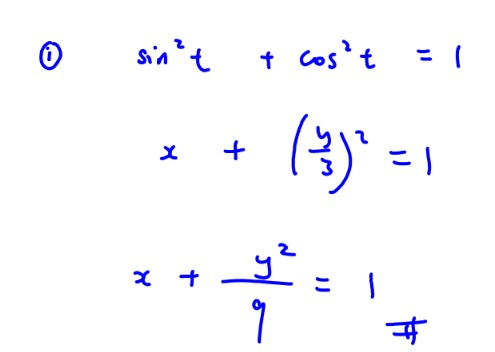

- (i)
- (ii)
- (iii)
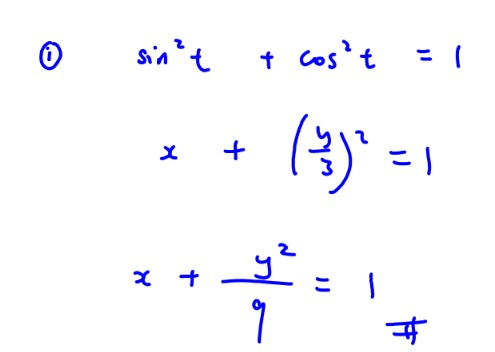


Share with your friends!
2016 ACJC MYE Q4
The curve $C$ has parametric equation $x=3-2\cos \,t$, $y=-\tan \,t$ for $0<t<\frac{\pi }{2}$. Using differentiation, show that the curve $C$ does not have any stationary point.
[2]
(i)
A point $Q$ on $C$ has parameter $t=\frac{\pi }{6}$. Find the equation of the tangent at $Q$, leaving your answer in exact form.
[2]
(i) A point $Q$ on $C$ has parameter $t=\frac{\pi }{6}$. Find the equation of the tangent at $Q$, leaving your answer in exact form.
[2]
(ii)
Find the cartesian equation of the locus of the mid-point of $(3-2\cos \,t,\,-\tan \,t)$ and $(-3,0)$ as $t$ varies.
[3]
(ii) Find the cartesian equation of the locus of the mid-point of $(3-2\cos \,t,\,-\tan \,t)$ and $(-3,0)$ as $t$ varies.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- -
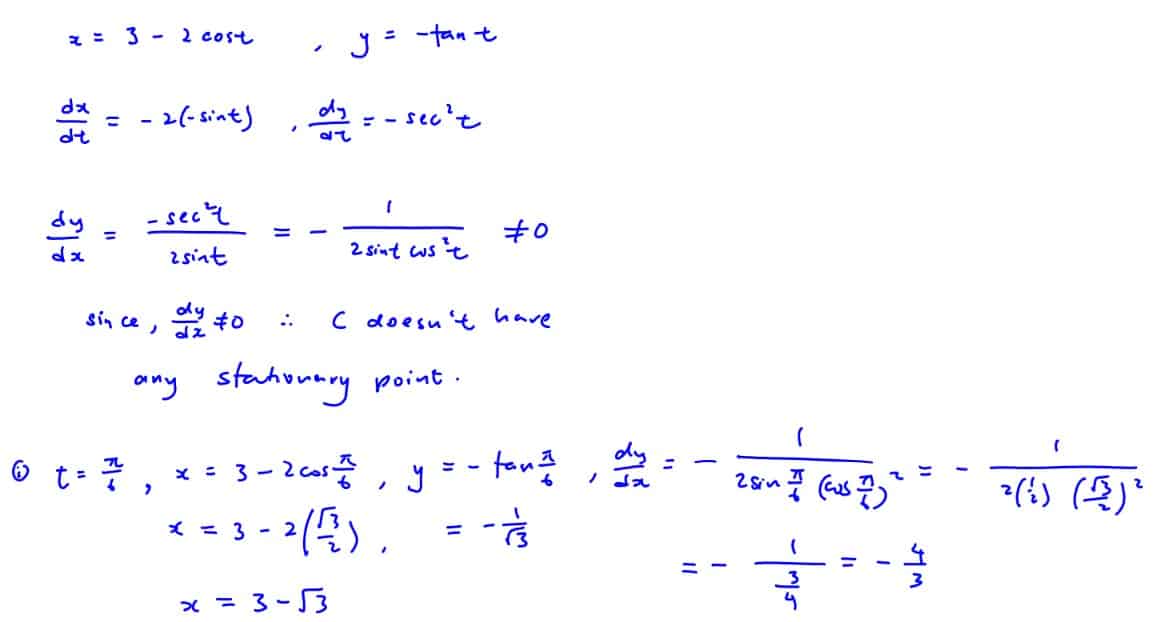
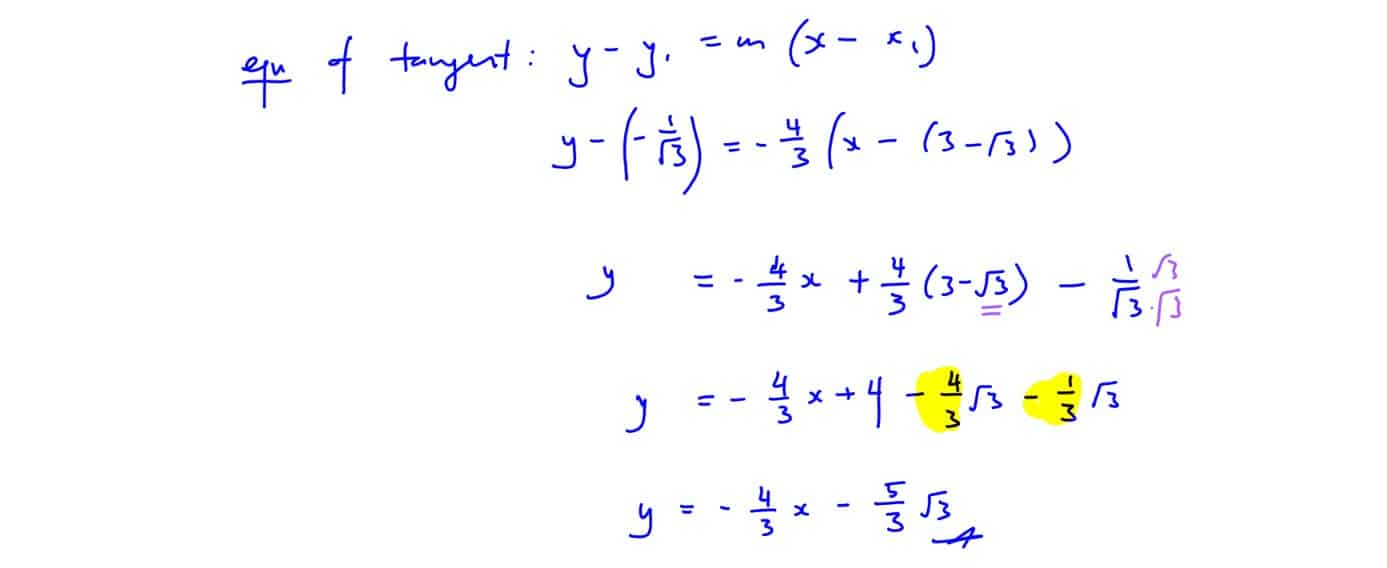
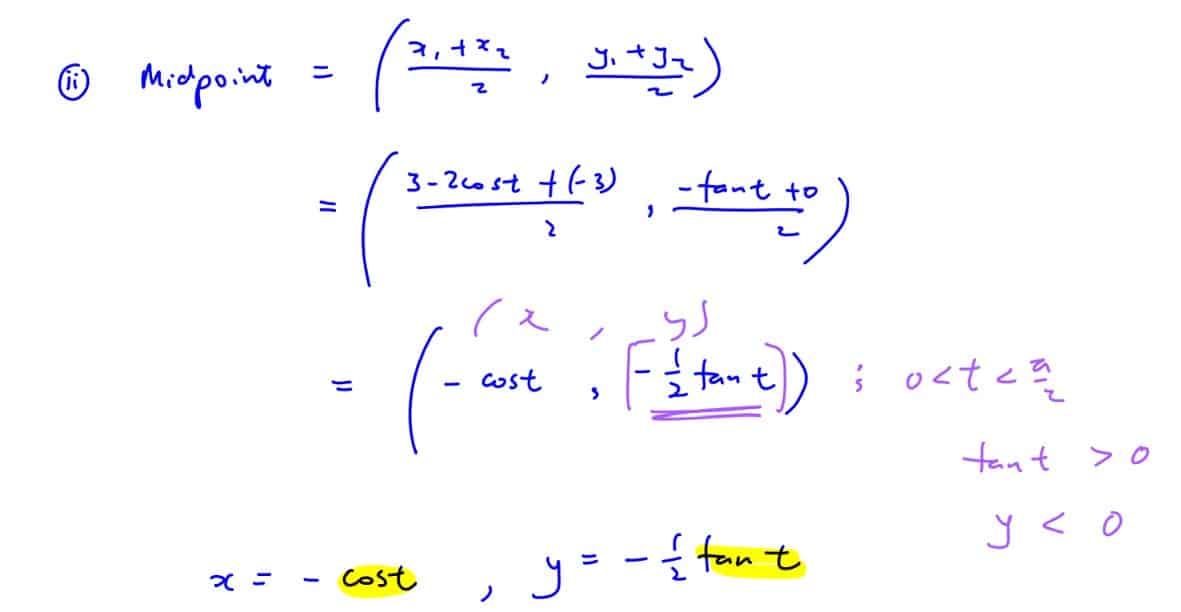
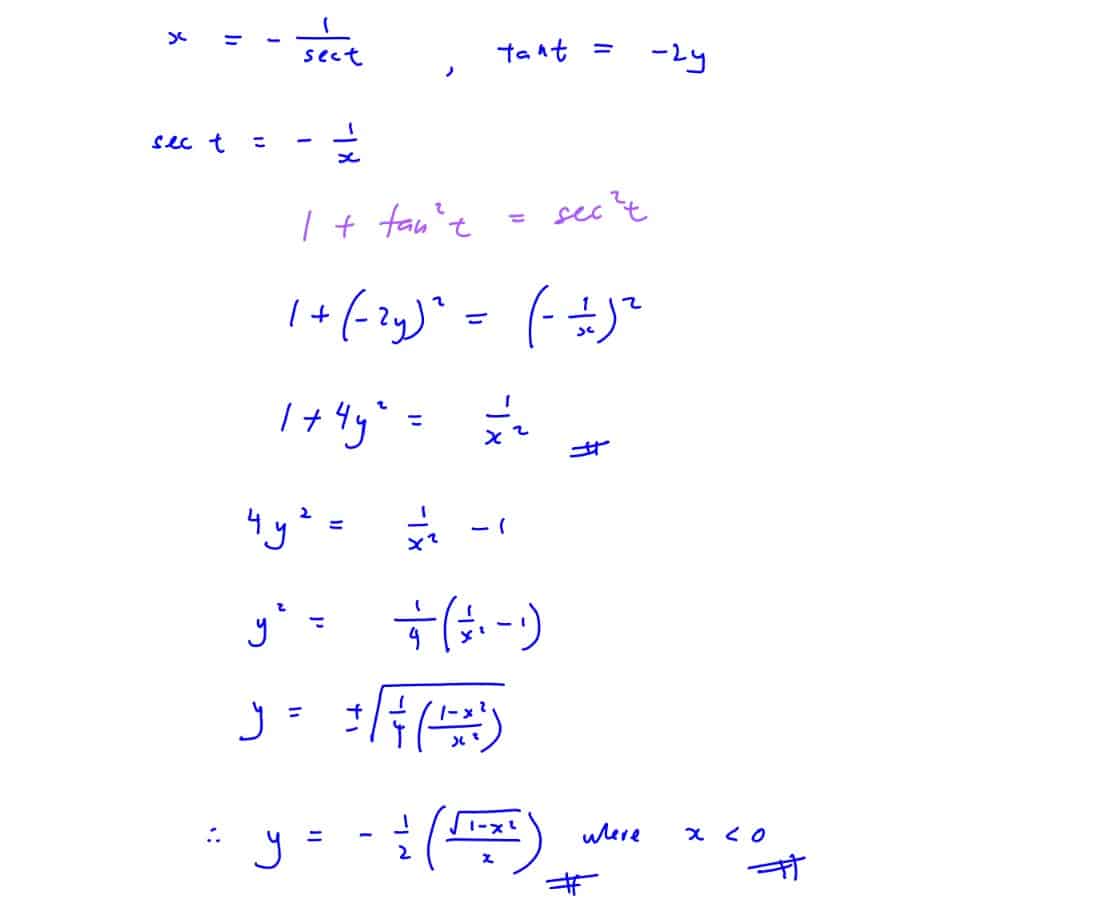
- (i)
- (ii)
- -
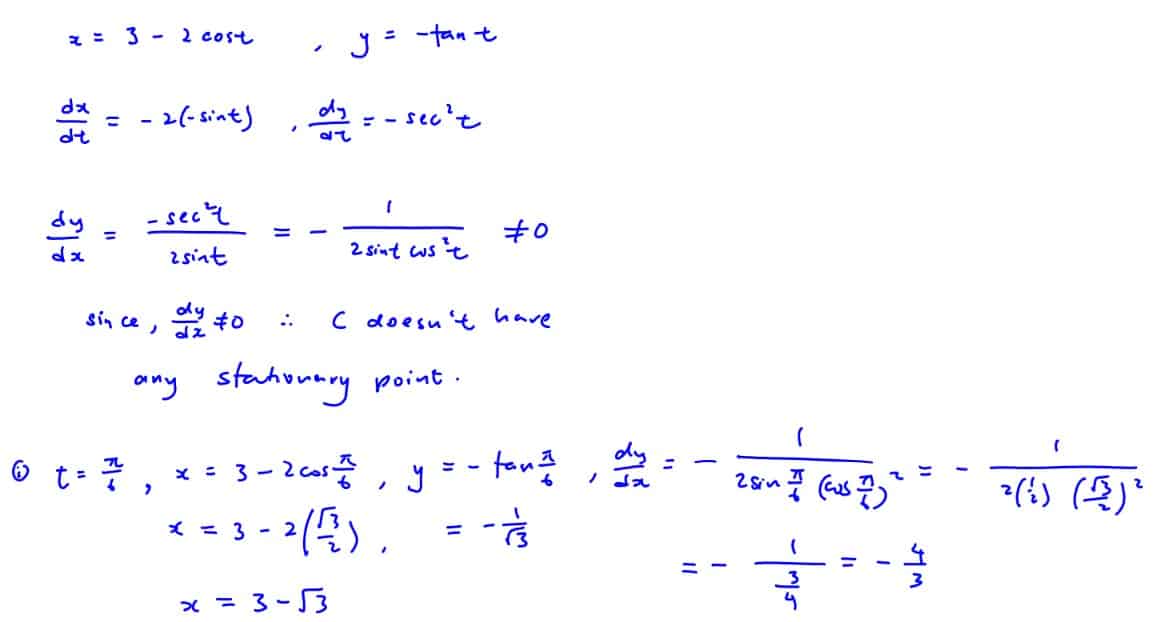
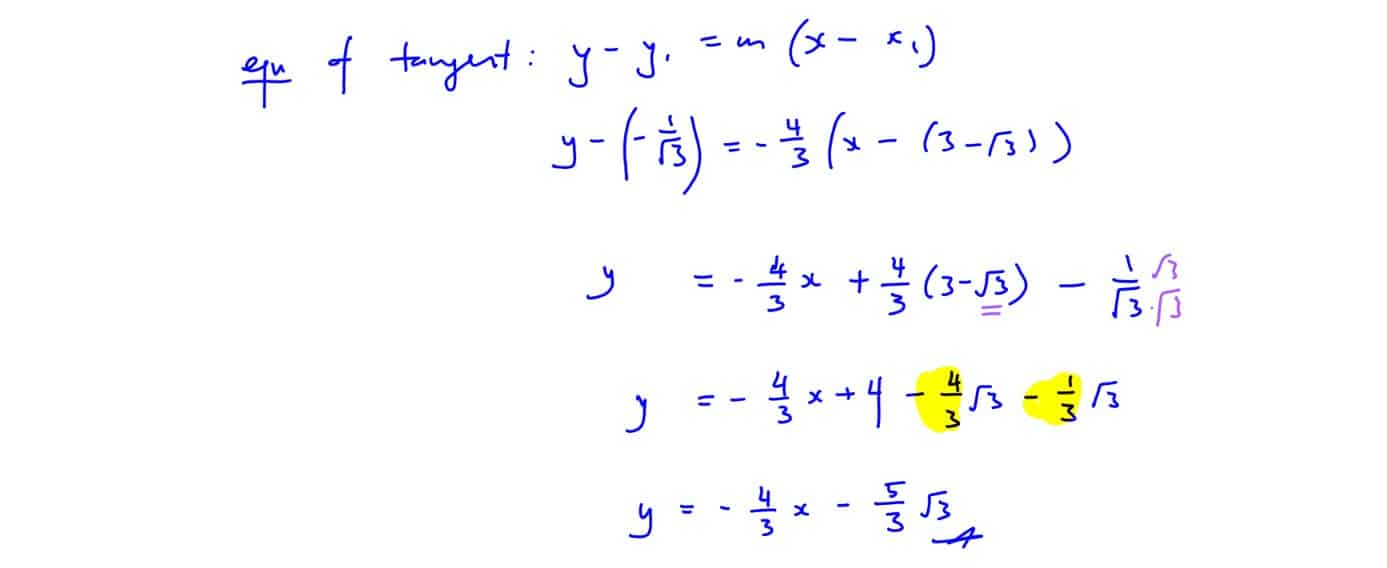
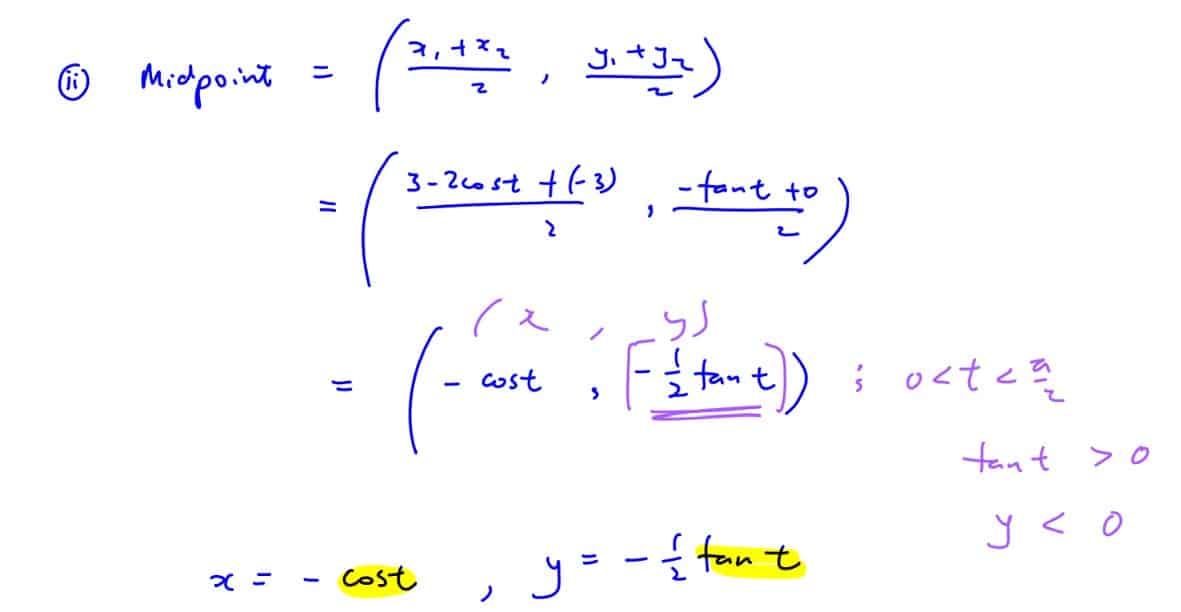
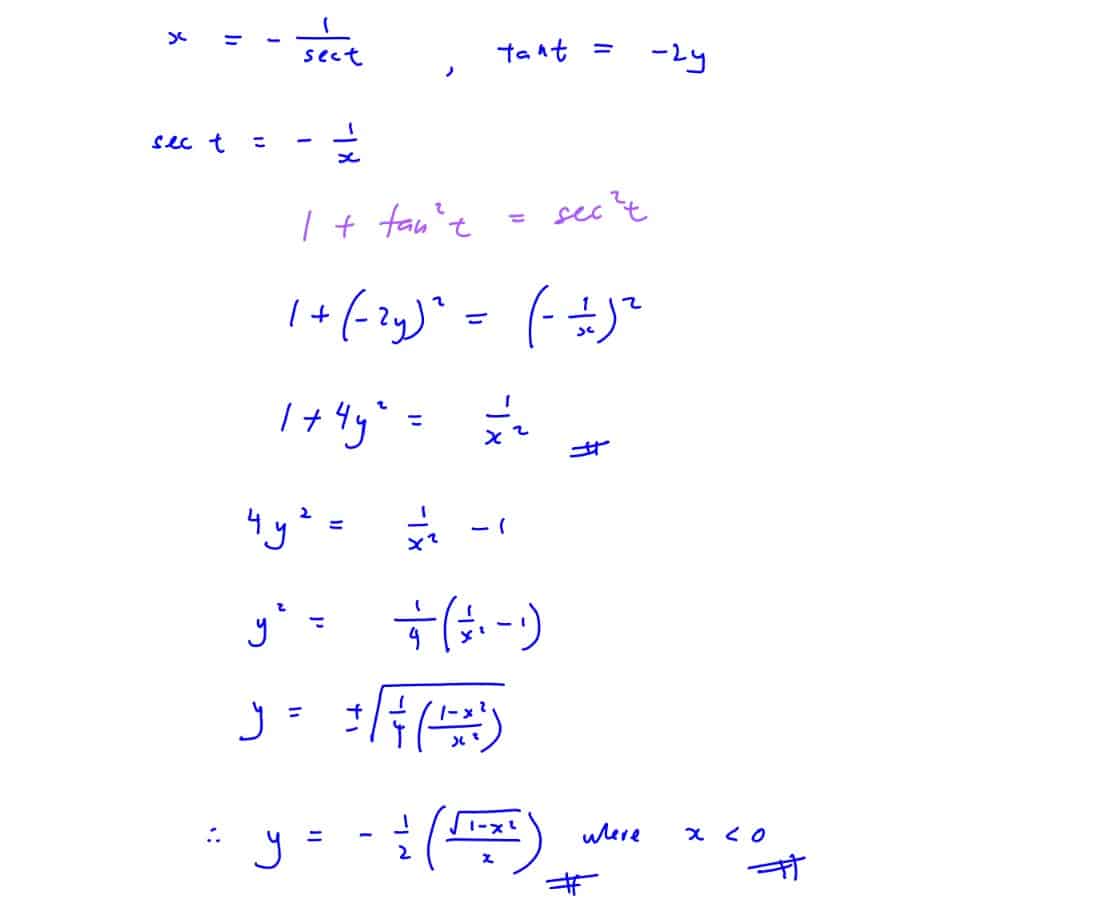
Share with your friends!
2018 TJC P2 Q1
A curve $C$ has parametric equations
$x=2{{e}^{t}}$, $y={{t}^{3}}-t$,
where $-1\le t\le \frac{3}{2}$.
(i)
Find $\frac{\text{d}y}{\text{d}x}$ in terms of $t$. Hence find the exact equations of the normals to the curve which are parallel to the $y$-axis.
[3]
(i) Find $\frac{\text{d}y}{\text{d}x}$ in terms of $t$. Hence find the exact equations of the normals to the curve which are parallel to the $y$-axis.
[3]
(ii)
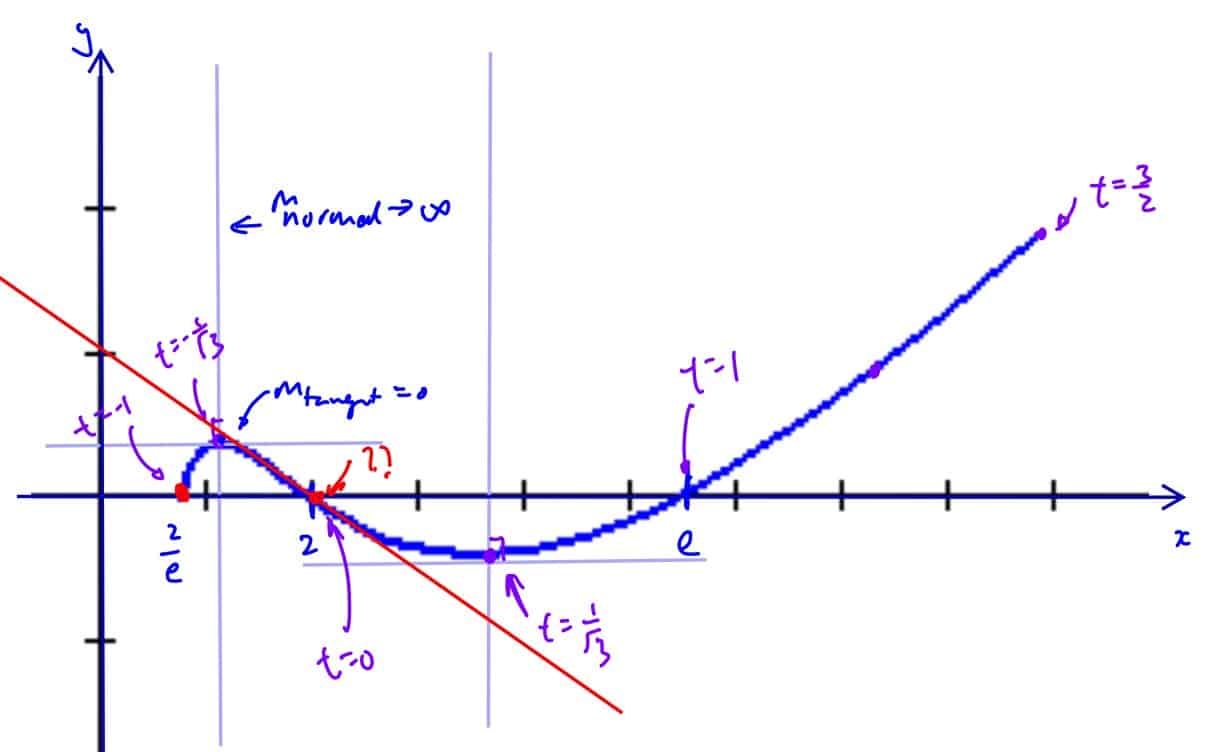
Sketch the curve $C$.
(ii) Sketch the curve $C$.
(iii)
Find the equation of the tangent to $C$ at the point$\left( 2{{e}^{a}},{{a}^{3}}-a \right)$. Find the possible exact values of $a$ such that the tangent cuts the $y$-axis at $y=1$.
[4]
(iii) Find the equation of the tangent to $C$ at the point$\left( 2{{e}^{a}},{{a}^{3}}-a \right)$. Find the possible exact values of $a$ such that the tangent cuts the $y$-axis at $y=1$.
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)



- (i)
- (ii)
- (iii)




Share with your friends!
2007 AJC P1 Q12 (b)
A curve is defined by the parametric equations
$x=a{{t}^{2}},\,y=2at.$
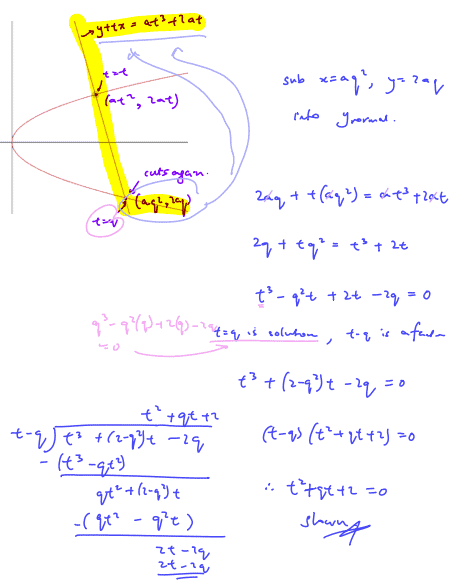
Show that the equation of the normal to the curve at the point $(a{{t}^{2}},\,2at)$ is at $y+tx=a{{t}^{3}}+2at$.
If the normal to the curve at the point $(a{{t}^{2}},\,2at)$ meets the curve again at the point $(a{{q}^{2}},\,2aq),$ show that ${{t}^{2}}+qt+2=0$.
Deduce that ${{q}^{2}}$ cannot be less than $8$.
Suggested Handwritten and Video Solutions
- I
- II
- III
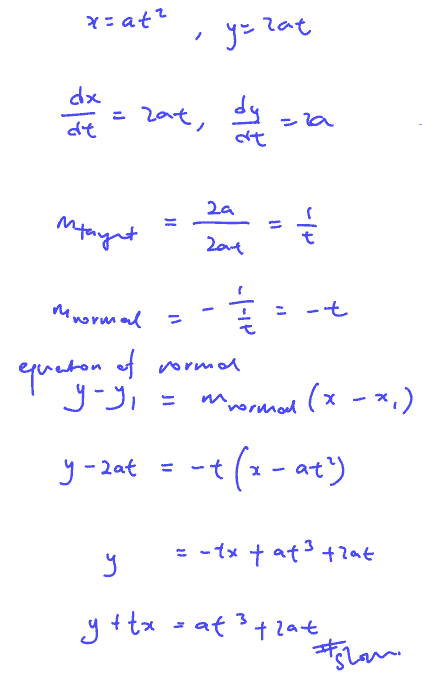
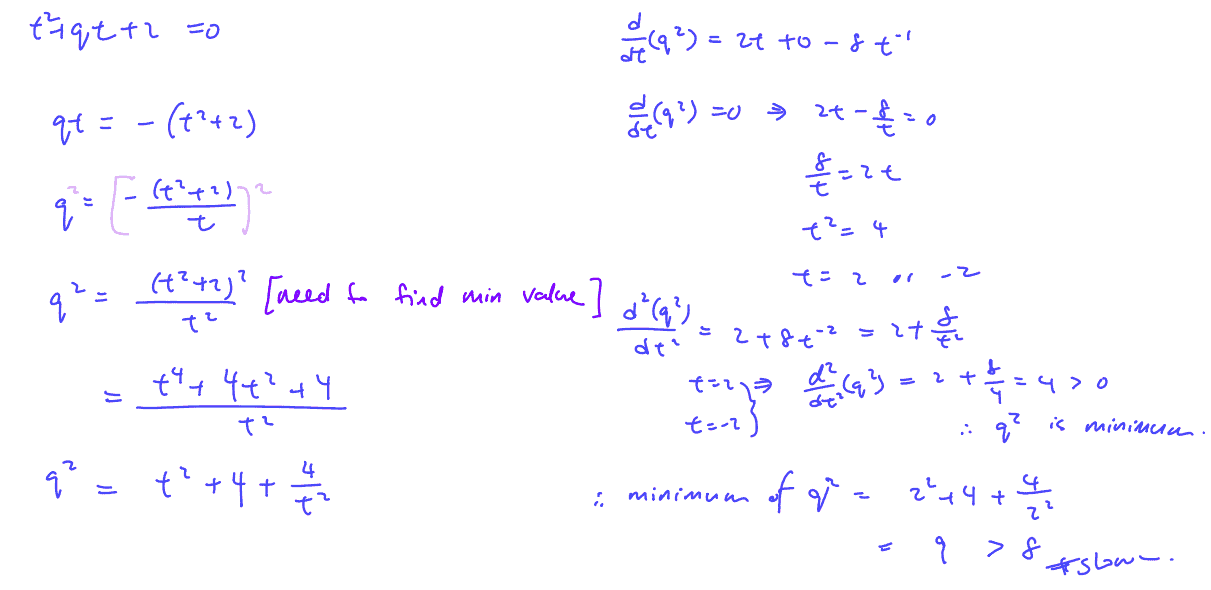
- I
- II
- III
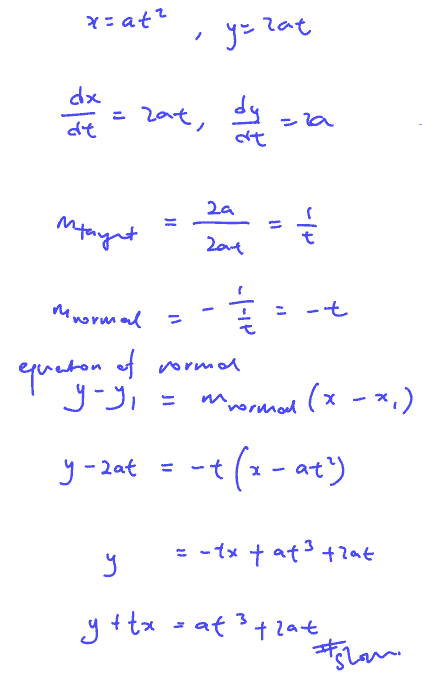

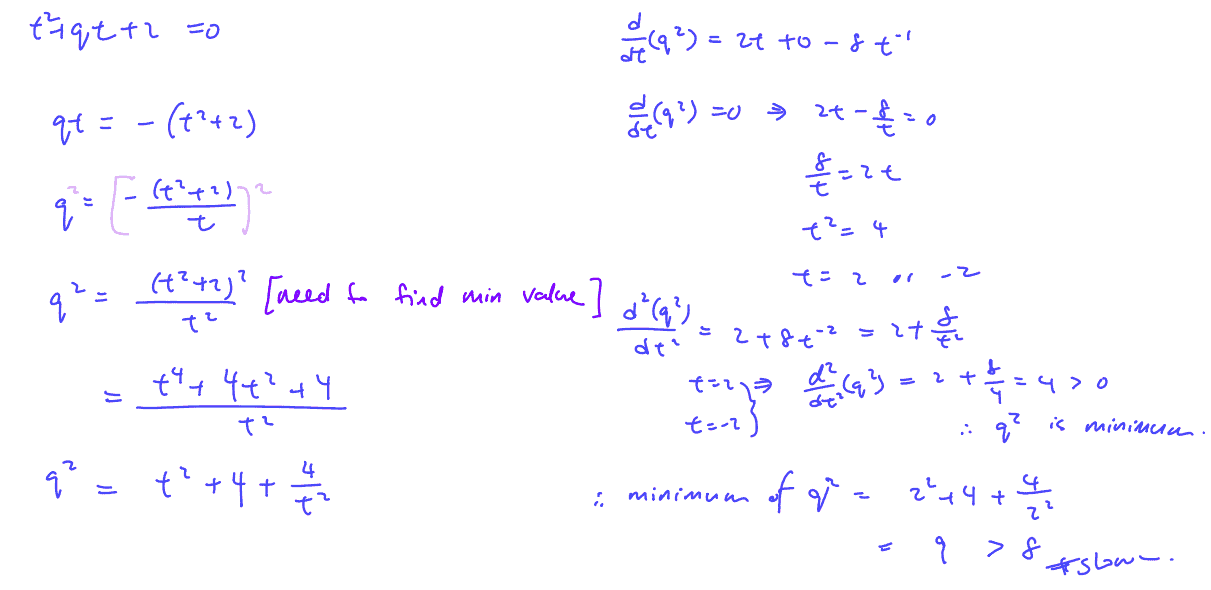
Share with your friends!
2018 EJC P1 Q3
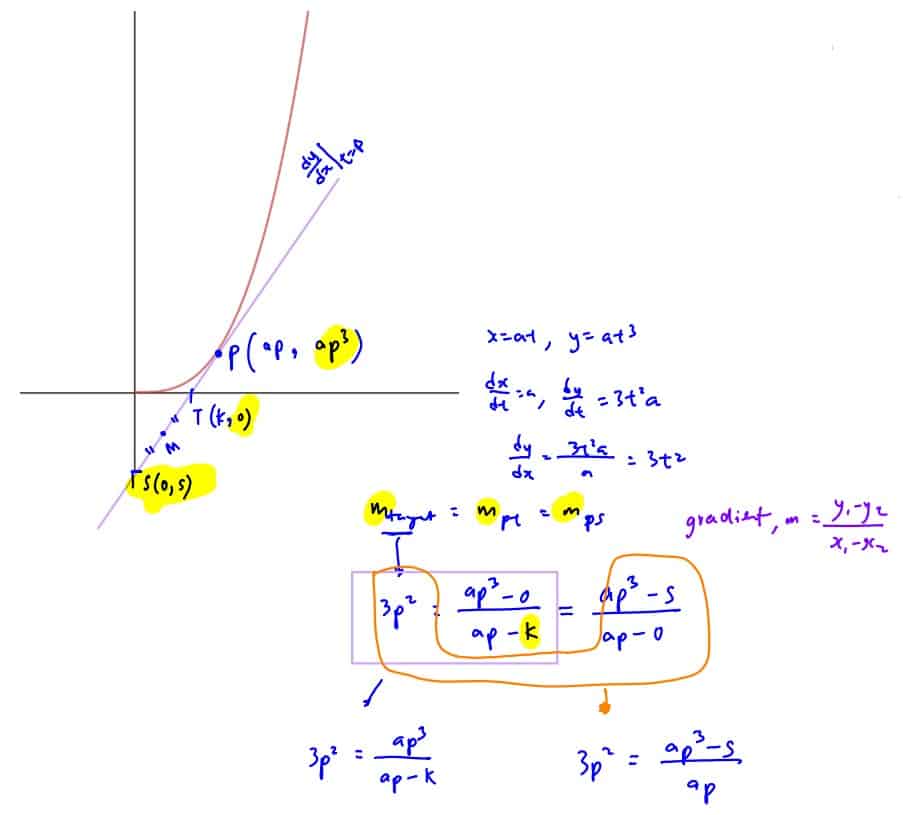
The parametric equations of curve $C$, is given as $x=at$, $y=a{{t}^{3}}$, where $a$ is a positive constant.
(i)
The point $P$ on the curve has parameter $p$ and the tangent to the curve at point $P$ cuts the $y$-axis at $S$ and the $x$-axis at $T$. The point $M$ is the midpoint of $ST$. Find a Cartesian equation of the curve traced by $M$ as $p$ varies.
[5]
(i) The point $P$ on the curve has parameter $p$ and the tangent to the curve at point $P$ cuts the $y$-axis at $S$ and the $x$-axis at $T$. The point $M$ is the midpoint of $ST$. Find a Cartesian equation of the curve traced by $M$ as $p$ varies.
[5]
(ii)
Find the exact area bounded by curve $C$, the line $x=0$, $x=3$ and $x$-axis, giving your answer in terms of $a$.
[3]
(ii) Find the exact area bounded by curve $C$, the line $x=0$, $x=3$ and $x$-axis, giving your answer in terms of $a$.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
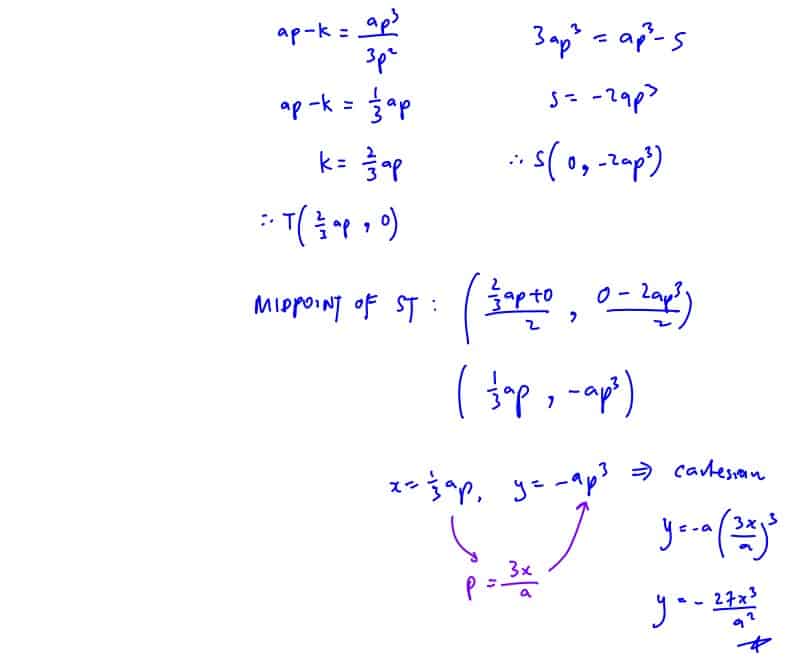

- (i)
- (ii)

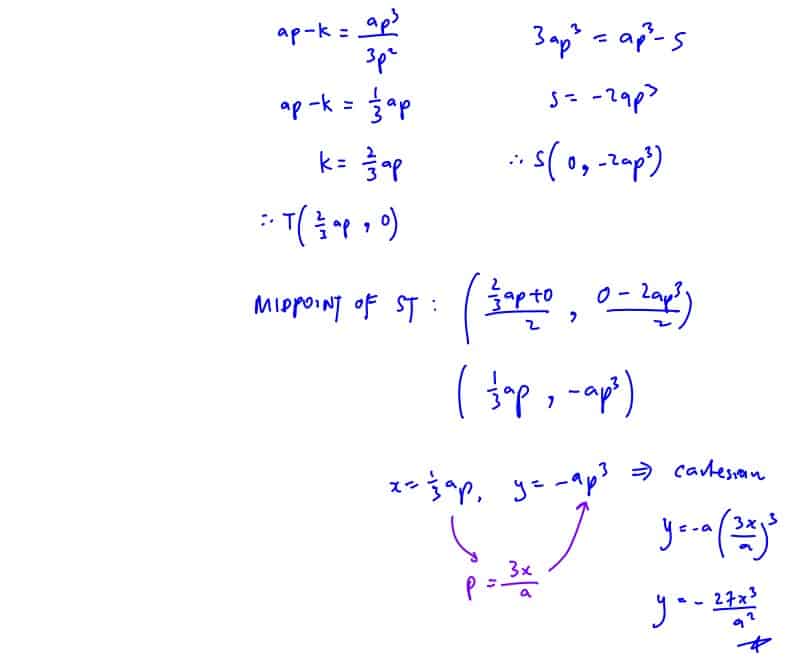

Share with your friends!
Download Parametric Equations Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
