A-Level H2 Math | 5 Essential Questions
Sigma Notation
Sigma Notation is a practice to express the sum of a lengthy series in a simple and concise way. The notation used for this is $\Sigma$ and it is always followed by the variable we are summing over. This symbol tells us to add up everything that follows it. The numbers we add together are called the terms of the series.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2017 EJC Promo Q7 (b) [Modified]
Given that $\sum\limits_{r=2}^{n}{\frac{1}{{{r}^{2}}-1}}=\frac{3}{4}-\frac{1}{2n}-\frac{1}{2\left( n+1 \right)}$,
(ii)
state $\sum\limits_{r=2}^{\infty }{\frac{1}{{{r}^{2}}-1}}$,
(ii) state $\sum\limits_{r=2}^{\infty }{\frac{1}{{{r}^{2}}-1}}$,
(iii)
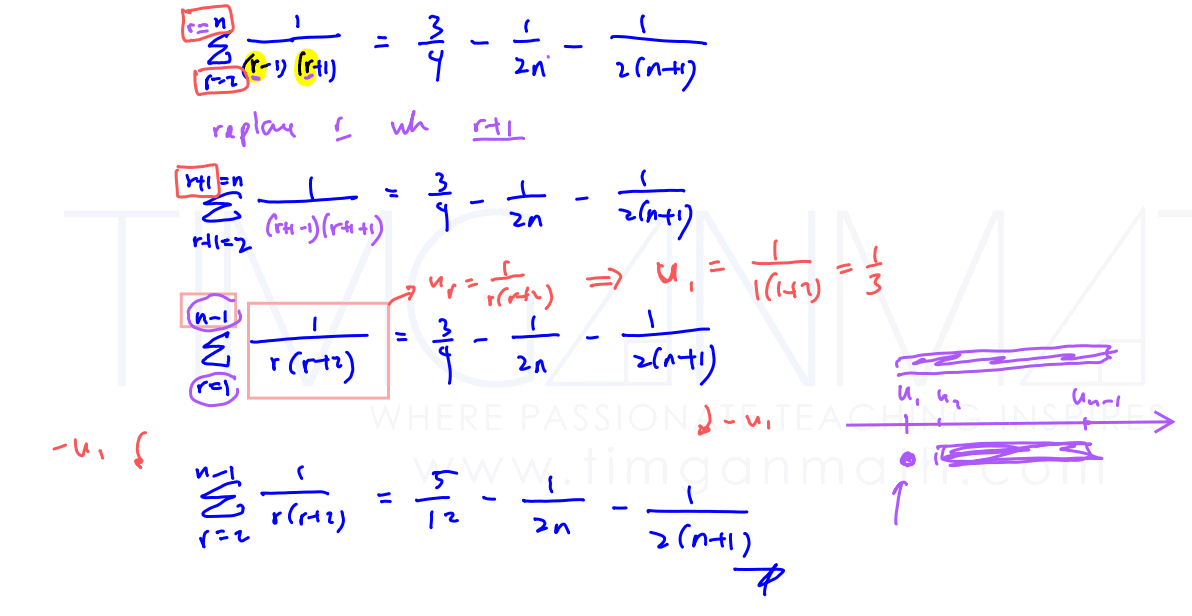
find $\sum\limits_{r=2}^{n-1}{\frac{1}{r(r+2)}}$.
(iii) find $\sum\limits_{r=2}^{n-1}{\frac{1}{r(r+2)}}$.
Suggested Handwritten and Video Solutions
- (ii)
- (iii)
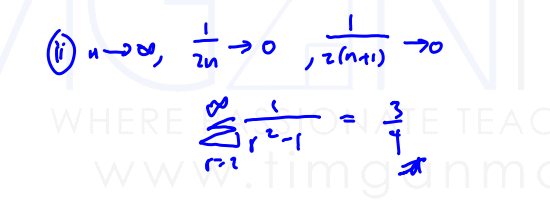
- (ii)
- (iii)
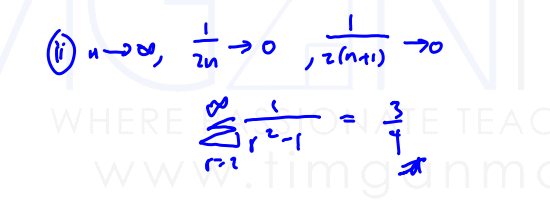

Share with your friends!
2018 YJC Promo Q13
The terms of a geometric progression ${{u}_{1}},{{u}_{2}},{{u}_{3}},{{u}_{4}},…$ are such that the sum to infinity is $81$ and the sum of the first $4$ terms is $80$.
If ${{u}_{1}}>100\,\,$and $\,\text{n}\ge \text{3}$,
(i)
[1]
[1]
(ii)
[3]
[3]
(iii)
[2]
[2]
(iv)
[2]
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)


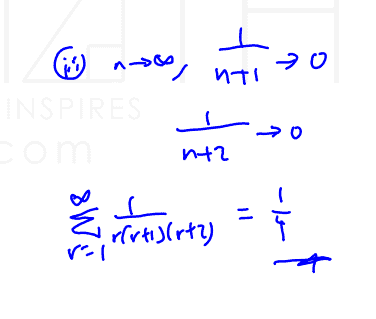
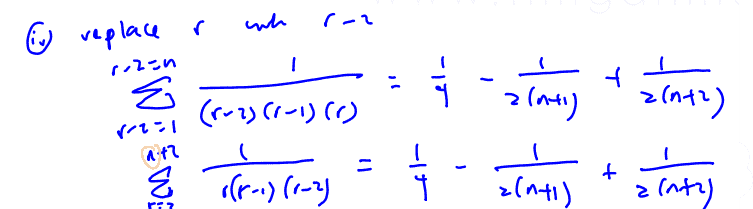
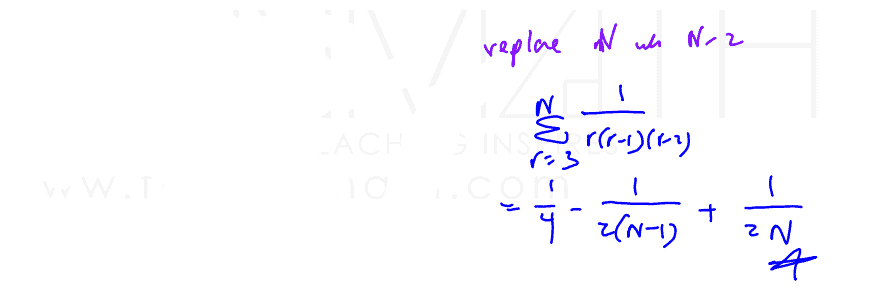
- (i)
- (ii)
- (iii)
- (iv)


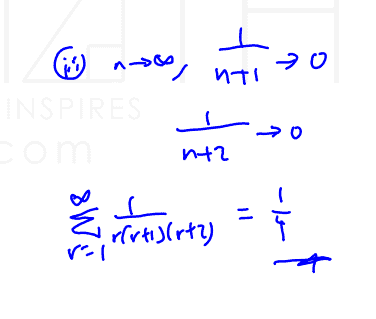
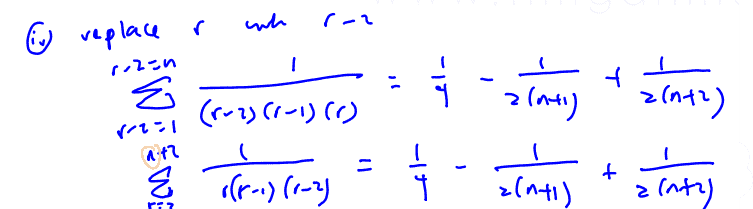
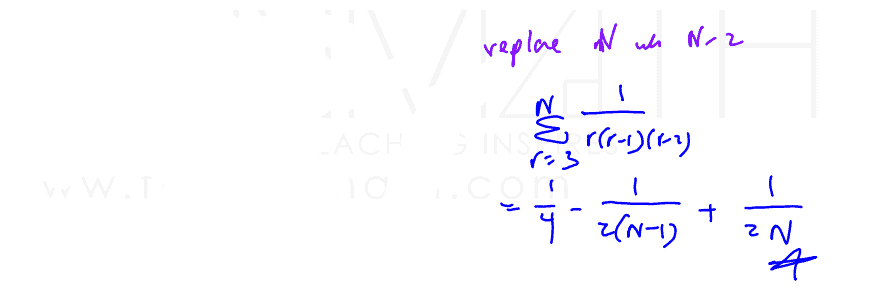
Share with your friends!
2019 DHS Promo Q2
Using the result $\sum\limits_{r=1}^{n}{\frac{r}{{{2}^{r}}}}=2-\frac{n+2}{{{2}^{n}}}$, show that $\sum\limits_{r=1}^{n}{\left( r-n \right)\left( {{2}^{-r}}+1 \right)}$ can be expressed in the form $C\left( 1-\frac{1}{{{2}^{n}}} \right)+Dn\left( n+1 \right)$, where $C$ and $D$ are constants to be determined.
[4]
Suggested Handwritten and Video Solutions
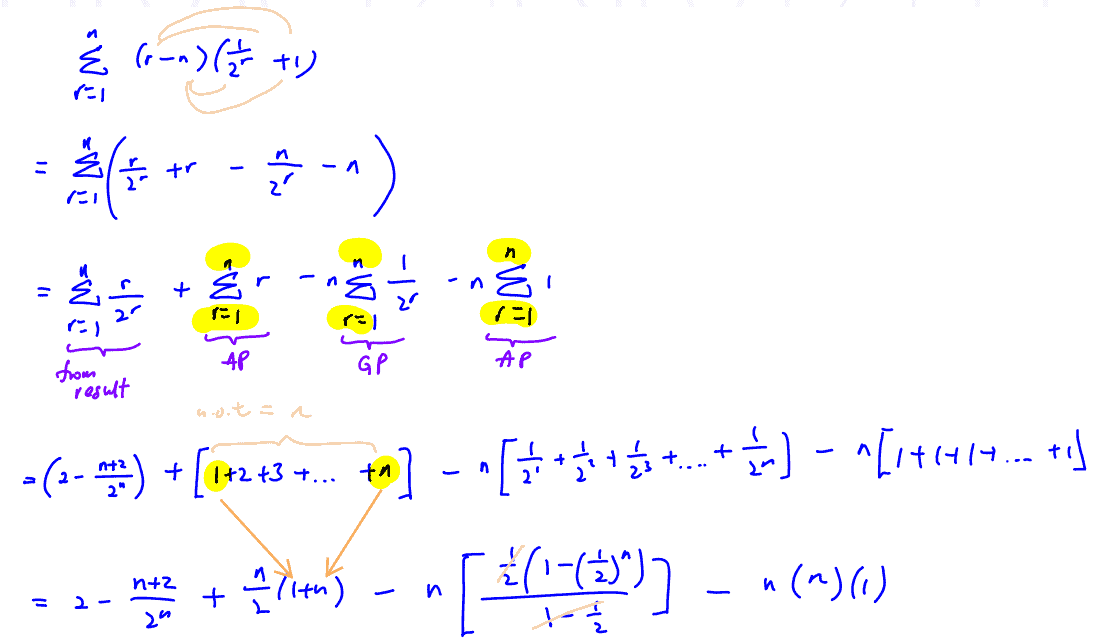
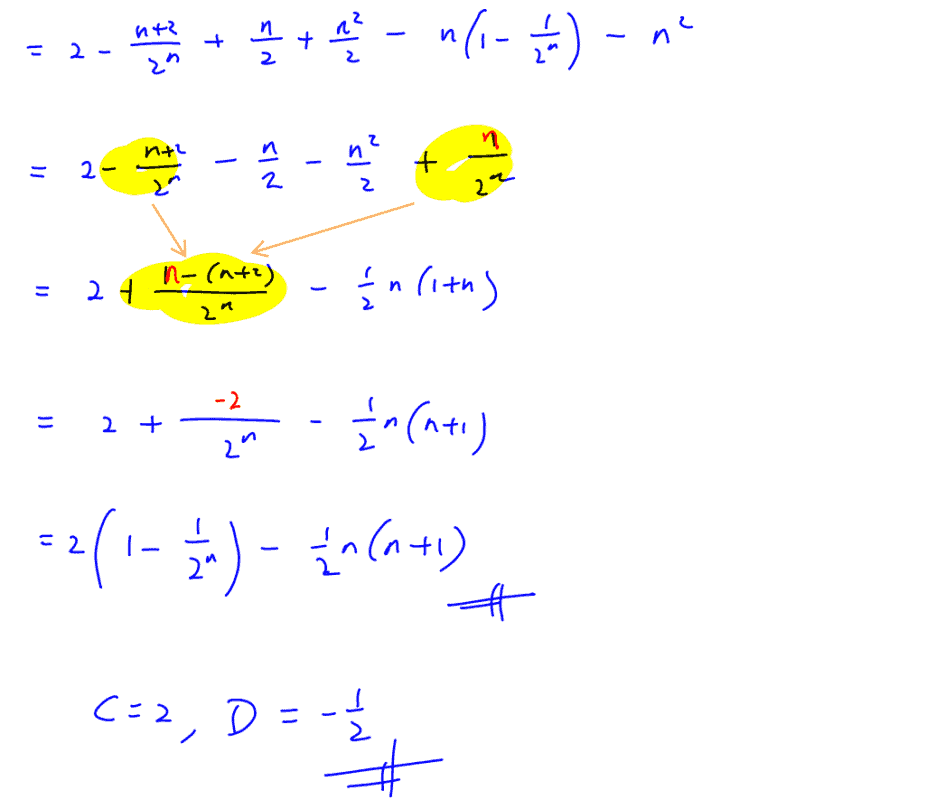
Share with your friends!
2017 VJC P1 Q8
It is given that $\sum\limits_{r=1}^{n}{\frac{{{r}^{2}}}{{{3}^{r}}}}=\frac{3}{2}-\frac{{{n}^{2}}+3n+3}{2\left( {{3}^{n}} \right)}$ .
(i)
Find $\sum\limits_{r=1}^{\infty }{\frac{{{r}^{2}}+{{\left( -1 \right)}^{r}}}{{{3}^{r}}}}$.
[3]
(i) Find $\sum\limits_{r=1}^{\infty }{\frac{{{r}^{2}}+{{\left( -1 \right)}^{r}}}{{{3}^{r}}}}$.
[3]
(ii)
Show that $\sum\limits_{r=4}^{n}{\frac{{{\left( r-2 \right)}^{2}}}{{{3}^{r-2}}}}=\frac{p}{q}-\frac{a{{n}^{2}}-an+a}{2\left( {{3}^{n-2}} \right)}$, where $a$, $p$ and $q$ are integers to be determined.
[5]
[5]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
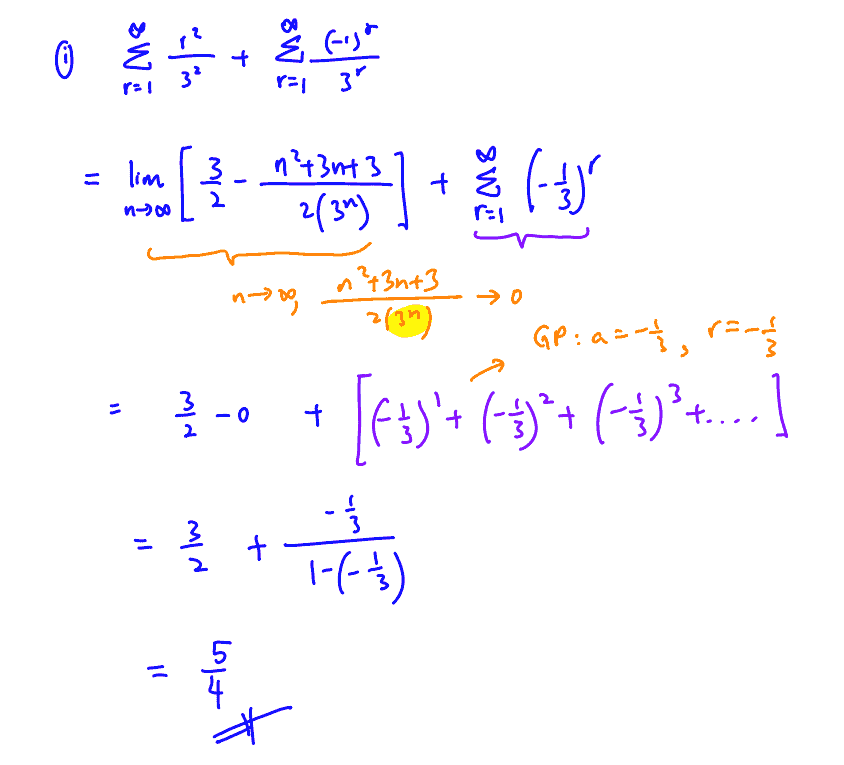
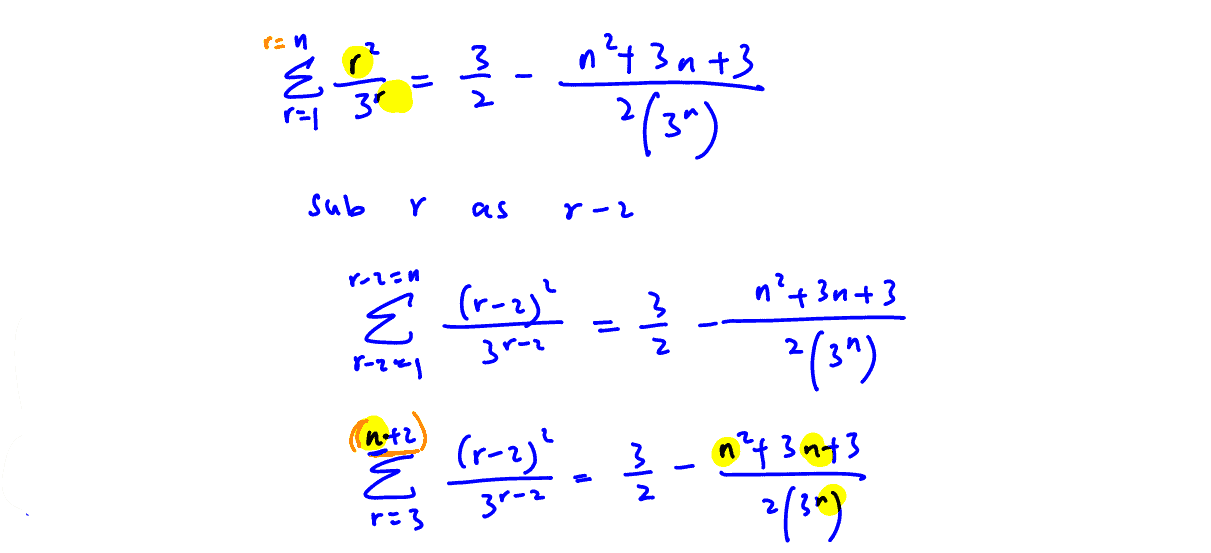
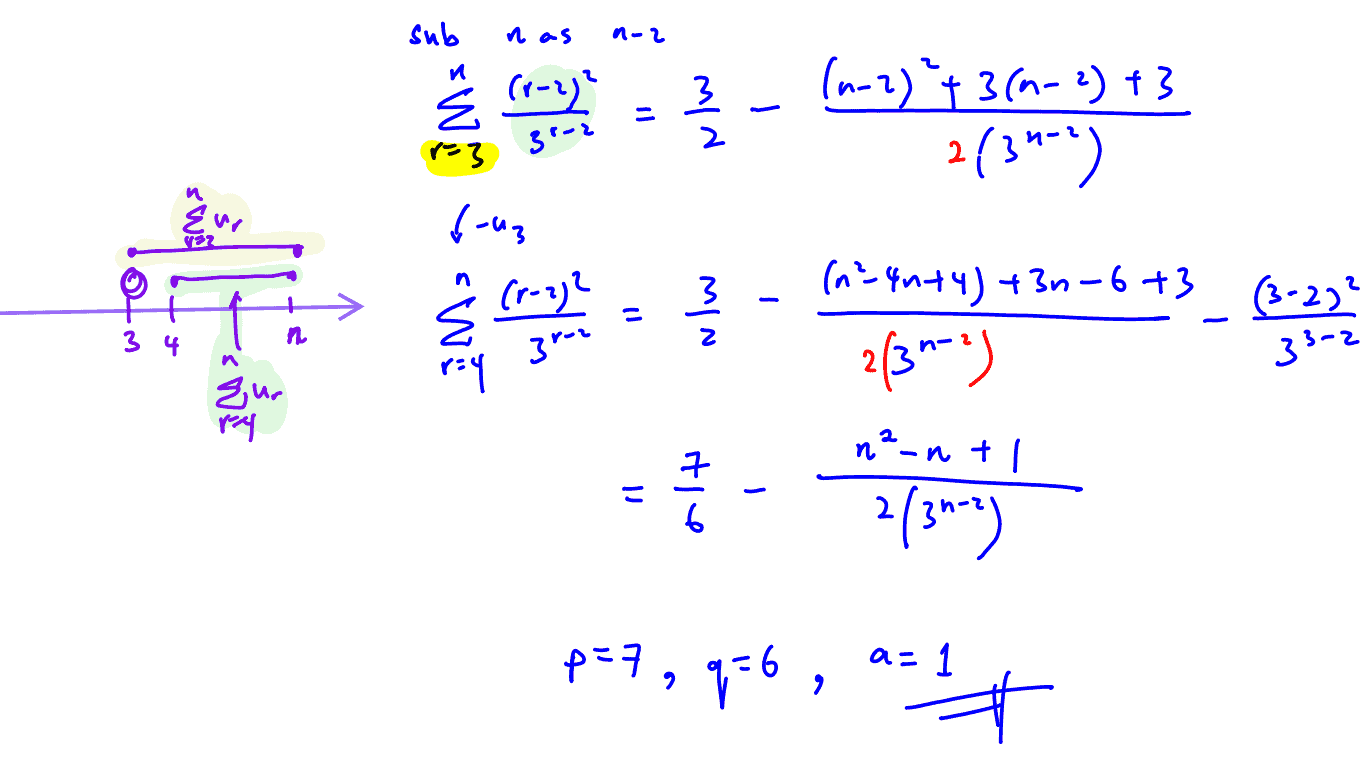
- (i)
- (ii)
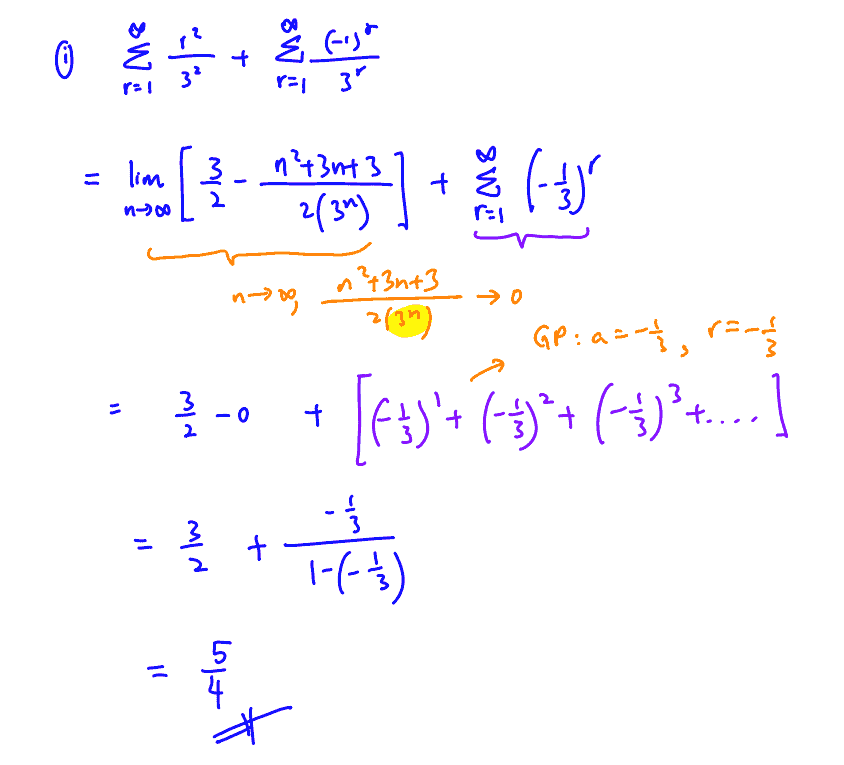
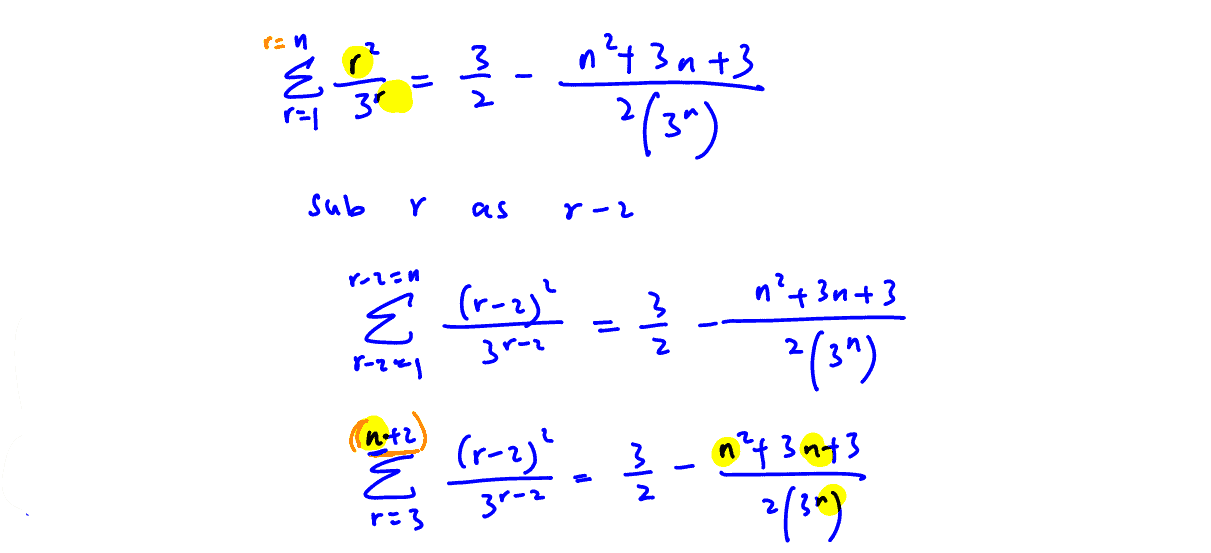
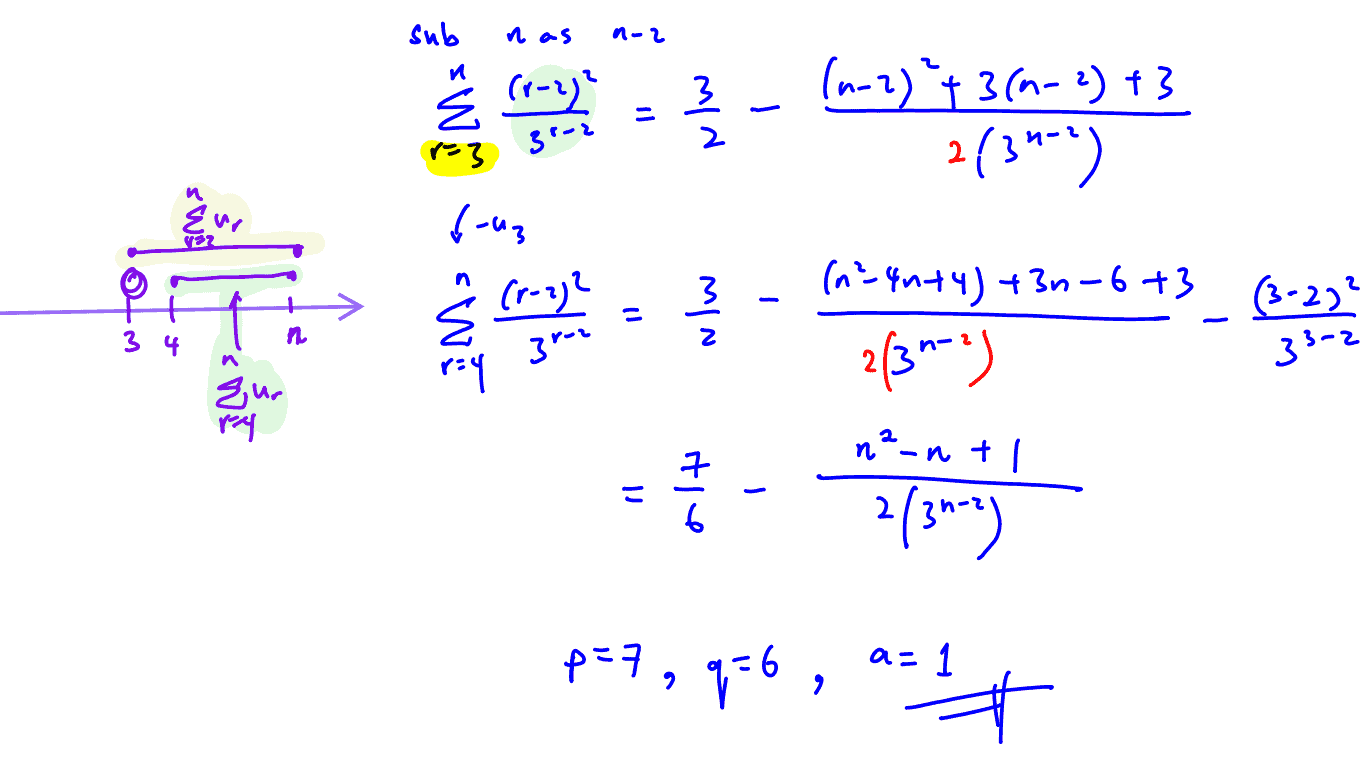
Share with your friends!
2020 EJC P1 Q10
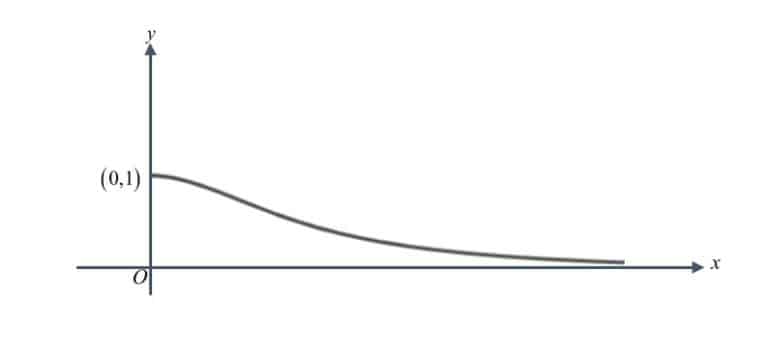
The diagram shows the graph of $y=\frac{1}{{{x}^{2}}+1}$ when $x>0$.
(i)
[2]
[2]
(ii)
$\frac{1}{{{\left( k+1 \right)}^{2}}+1}<{{\tan }^{-1}}\left( k+1 \right)-{{\tan }^{-1}}k<\frac{1}{{{k}^{2}}+1}$ for $k\in {{\mathbb{Z}}^{+}}$.
[2]
$\frac{1}{{{\left( k+1 \right)}^{2}}+1}<{{\tan }^{-1}}\left( k+1 \right)-{{\tan }^{-1}}k<\frac{1}{{{k}^{2}}+1}$ for $k\in {{\mathbb{Z}}^{+}}$.
[2]
(iii)
${{\tan }^{-1}}x-{{\tan }^{-1}}y={{\tan }^{-1}}\frac{x-y}{1+xy}$, where $x>y>0$.
[2]
${{\tan }^{-1}}x-{{\tan }^{-1}}y={{\tan }^{-1}}\frac{x-y}{1+xy}$, where $x>y>0$.
[2]
(iv)
By considering parts (ii) and (iii), prove by the method of differences that
$\sum\limits_{k=1}^{n}{\frac{1}{{{\left( k+1 \right)}^{2}}+1}}<{{\tan }^{-1}}\left( \frac{n}{n+2} \right)<\sum\limits_{k=1}^{n}{\frac{1}{{{k}^{2}}+1}}$
[4]
(iv) By considering parts (ii) and (iii), prove by the method of differences that
$\sum\limits_{k=1}^{n}{\frac{1}{{{\left( k+1 \right)}^{2}}+1}}<{{\tan }^{-1}}\left( \frac{n}{n+2} \right)<\sum\limits_{k=1}^{n}{\frac{1}{{{k}^{2}}+1}}$
[4]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
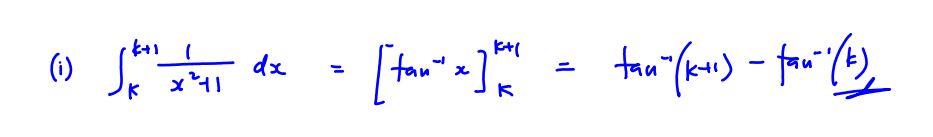



- (i)
- (ii)
- (iii)
- (iv)
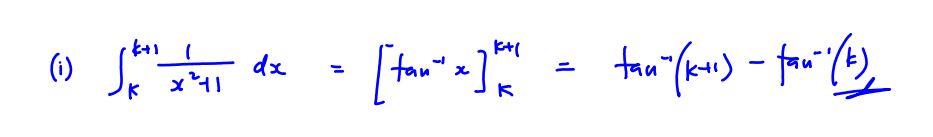



Share with your friends!
Download Sigma Notation Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
