A-Level H2 Math | 5 Essential Questions
Techniques of Integration
Integration is a fundamental topic in Mathematics that studies the relationship between a whole and its parts. Integrals are used in arithmetic, science and engineering, especially where it is necessary to study the dynamics of variable quantities like temperature or pressure. This is an operation we use all the time, to find areas under graphs, the volume of a solid, and many others.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
ACJC Tutorial 21 – Integration II [Self Practice Questions] Q5
$\int{x\,\sin }\left( \frac{x}{2} \right)\,\text{d}x$
Suggested Handwritten and Video Solutions
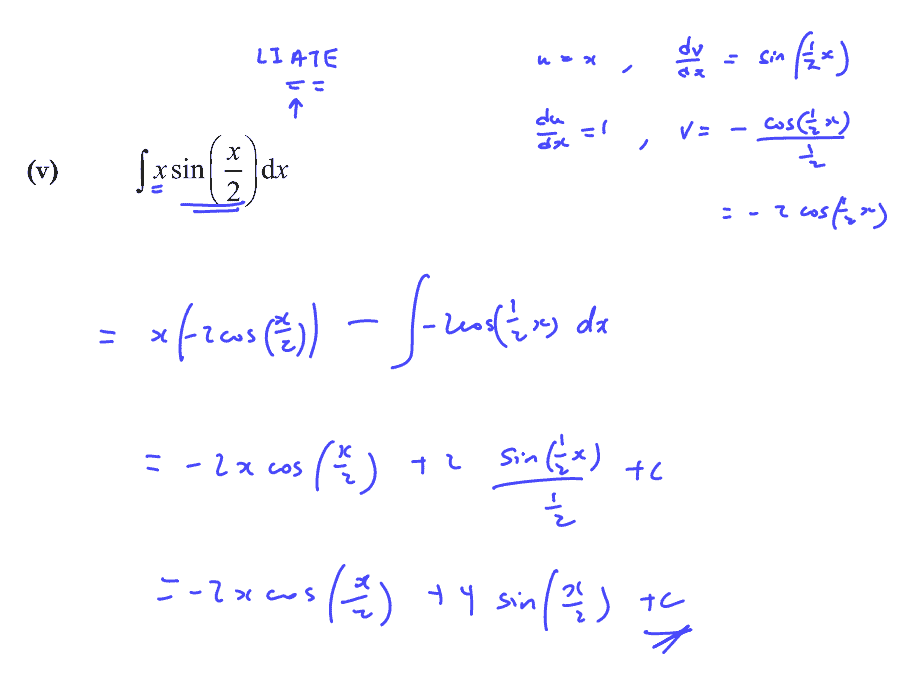
Share with your friends!
ACJC Tutorial 21 Q15
Evaluate $\int{\frac{1}{{{(1+{{x}^{2}})}^{2}}}\,\text{d}x}\,\,\,\,(\text{let}\,\,x=\,\tan \,\theta )$
Suggested Handwritten and Video Solutions


Share with your friends!
2020 EJC P1 Q2
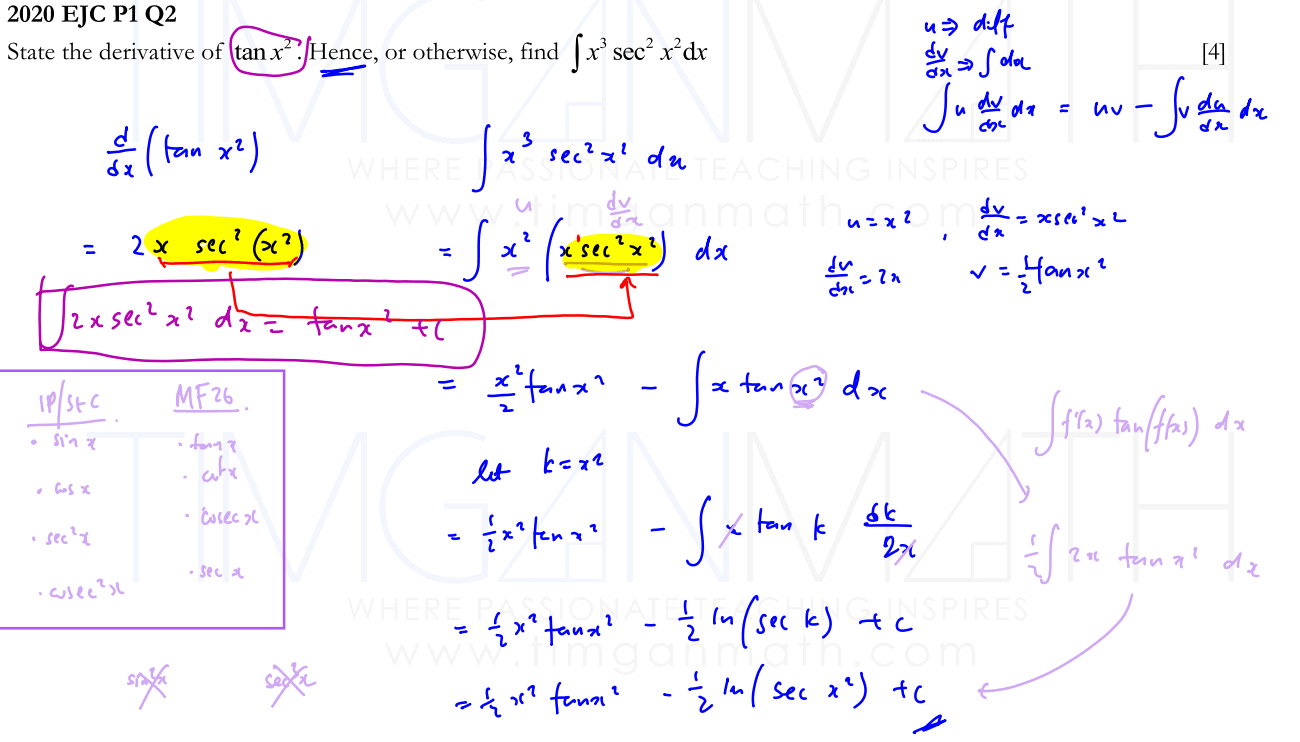
State the derivative of $\tan {{x}^{2}}$. Hence, or otherwise, find $\int{{{x}^{3}}{{\sec }^{2}}{{x}^{2}}\text{d}x}$
[4]
Suggested Handwritten and Video Solutions
Share with your friends!
2020 NYJC J2 CT P1 Q6
(a)
(i)
Show that $\tan 2\theta =\frac{2\tan \theta }{1-{{\tan }^{2}}\theta }$ using the addition formula from the List of Formulae (MF26).
[1]
(i) Show that $\tan 2\theta =\frac{2\tan \theta }{1-{{\tan }^{2}}\theta }$ using the addition formula from the List of Formulae (MF26).
[1]
(ii)
By using the substitution $x=\tan \theta $, or otherwise, find the exact value of $\int_{0}^{1}{{{\tan }^{-1}}\left( \frac{2x}{1-{{x}^{2}}} \right)}\,\text{d}x$.
[5]
(ii) By using the substitution $x=\tan \theta $, or otherwise, find the exact value of $\int_{0}^{1}{{{\tan }^{-1}}\left( \frac{2x}{1-{{x}^{2}}} \right)}\,\text{d}x$.
[5]
(b)
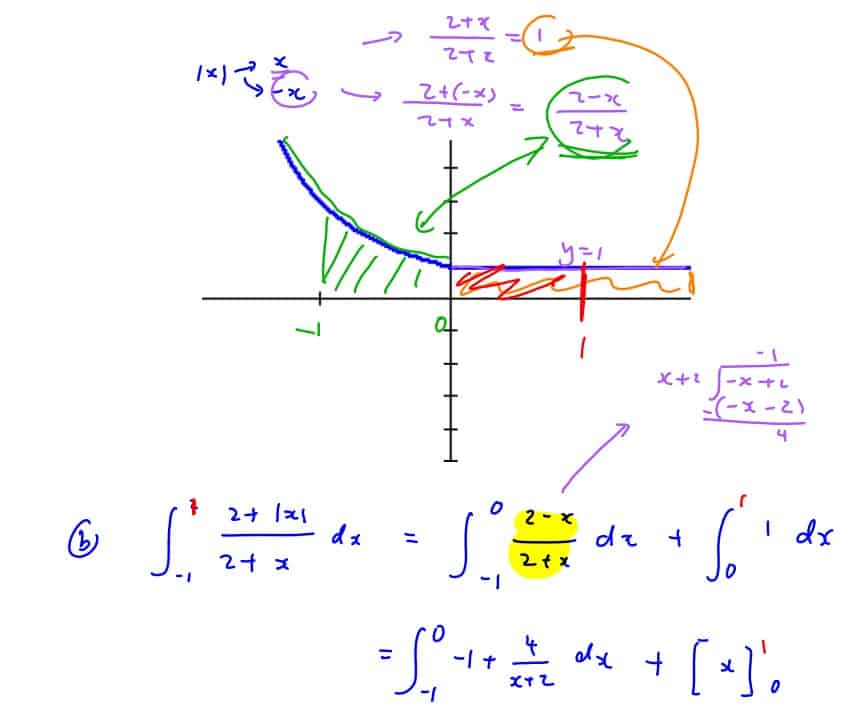
Find the exact value of $\int_{-1}^{1}{\frac{2+\left| x \right|}{2+x}\text{d}x}$.
[4]
(b) Find the exact value of $\int_{-1}^{1}{\frac{2+\left| x \right|}{2+x}\text{d}x}$.
[4]
Suggested Handwritten and Video Solutions
- (a) (i)
- (a) (ii)
- (b)
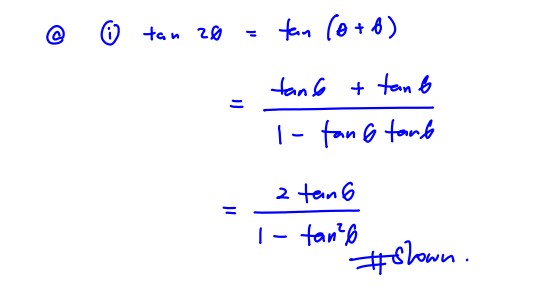

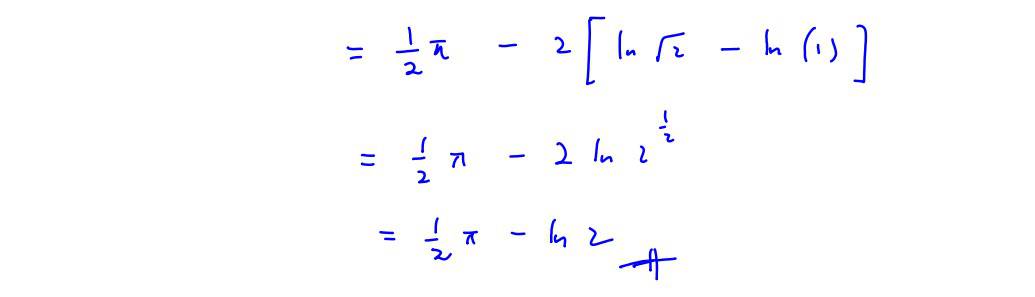
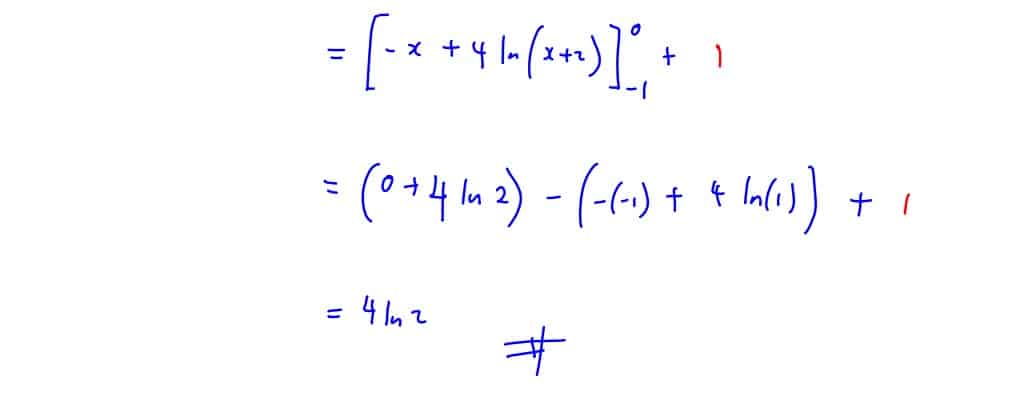
- (a) (i)
- (a) (ii)
- (b)
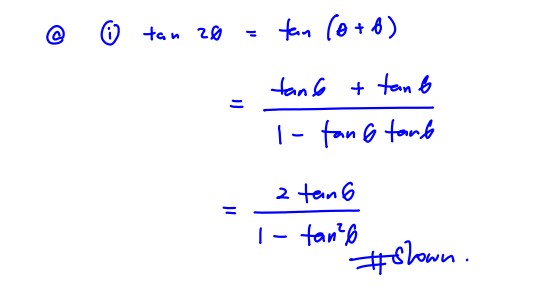

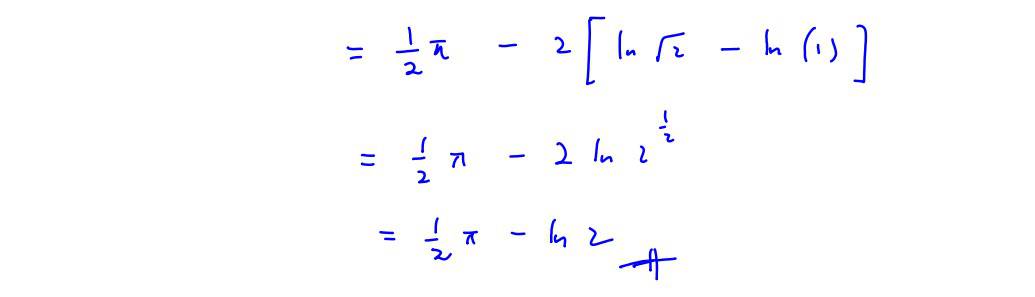

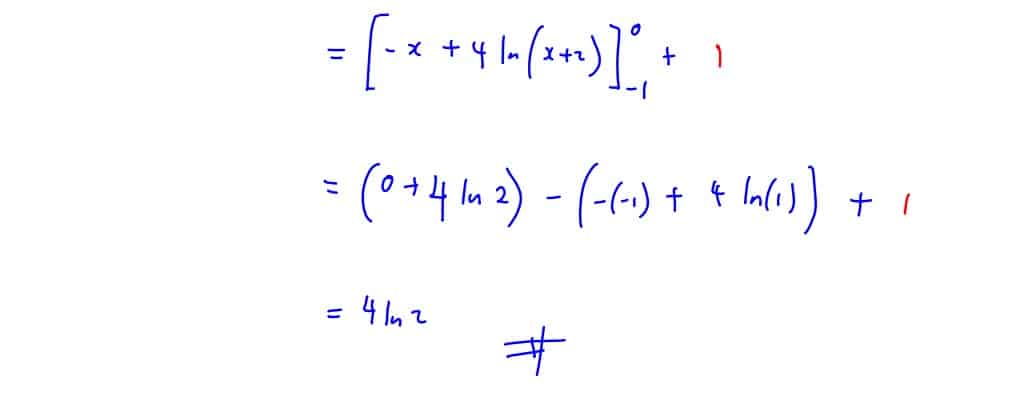
Share with your friends!
2014 AJC P1 Q9
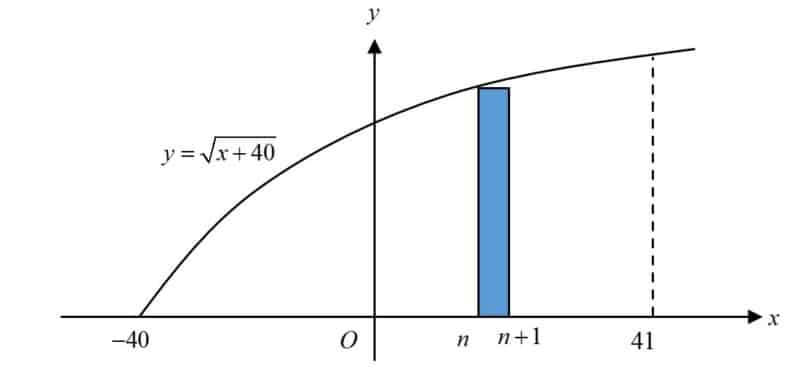
The graph of $y=\sqrt{x+40}$ is shown in the diagram below.
(i)
By considering the shaded rectangle, show that
$\sqrt{n+40}<\int\limits_{n}^{n+1}{\sqrt{x+40}\text{ d}x}$.
[1]
(i) By considering the shaded rectangle, show that
$\sqrt{n+40}<\int\limits_{n}^{n+1}{\sqrt{x+40}\text{ d}x}$.
[1]
(ii)
Deduce that
$\sqrt{1}+\sqrt{2}+\sqrt{3}+…+\sqrt{80}<$$\int\limits_{-40}^{41}{\sqrt{x+40}\text{ d}x}$.
[2]
(ii) Deduce that
$\sqrt{1}+\sqrt{2}+\sqrt{3}+…+\sqrt{80}<\int\limits_{-40}^{41}{\sqrt{x+40}\text{ d}x}$.
[2]
(iii)
Show also that
$\sqrt{n+41}>\int\limits_{n}^{n+1}{\sqrt{x+40}\text{ d}x}$.
[2]
(iii) Show also that
$\sqrt{n+41}>\int\limits_{n}^{n+1}{\sqrt{x+40}\text{ d}x}$.
[2]
(iv)
Deduce that
$\sqrt{1}+\sqrt{2}+\sqrt{3}+…+\sqrt{81}>$$\int\limits_{-40}^{41}{\sqrt{x+40}\text{ d}x}$.
[1]
(iv) Deduce that
$\sqrt{1}+\sqrt{2}+\sqrt{3}+…+\sqrt{81}>\int\limits_{-40}^{41}{\sqrt{x+40}\text{ d}x}$.
[1]
(v)
Hence, deduce that the value $a$, where $a\in \mathbb{Z}$, that satisfies the following inequality,
$9a<\sqrt{1}+\sqrt{2}+\sqrt{3}+…+\sqrt{81}<9\left( a+1 \right)$.
[2]
(v) Hence, deduce that the value $a$, where $a\in \mathbb{Z}$, that satisfies the following inequality,
$9a<\sqrt{1}+\sqrt{2}+\sqrt{3}+…+\sqrt{81}<9\left( a+1 \right)$.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)
- (v)
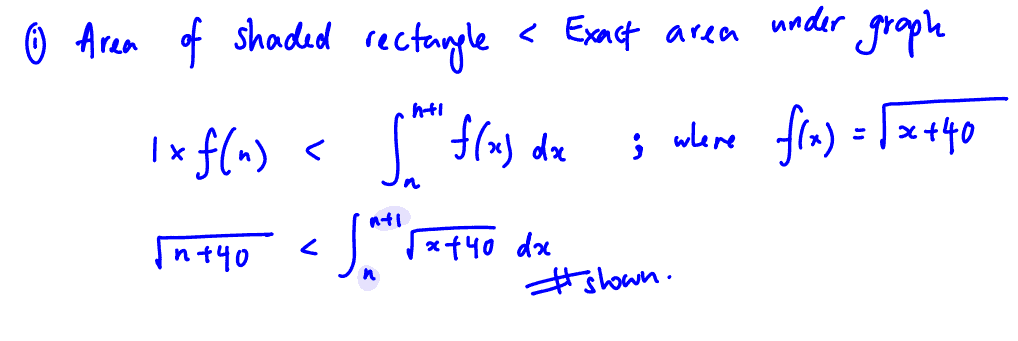

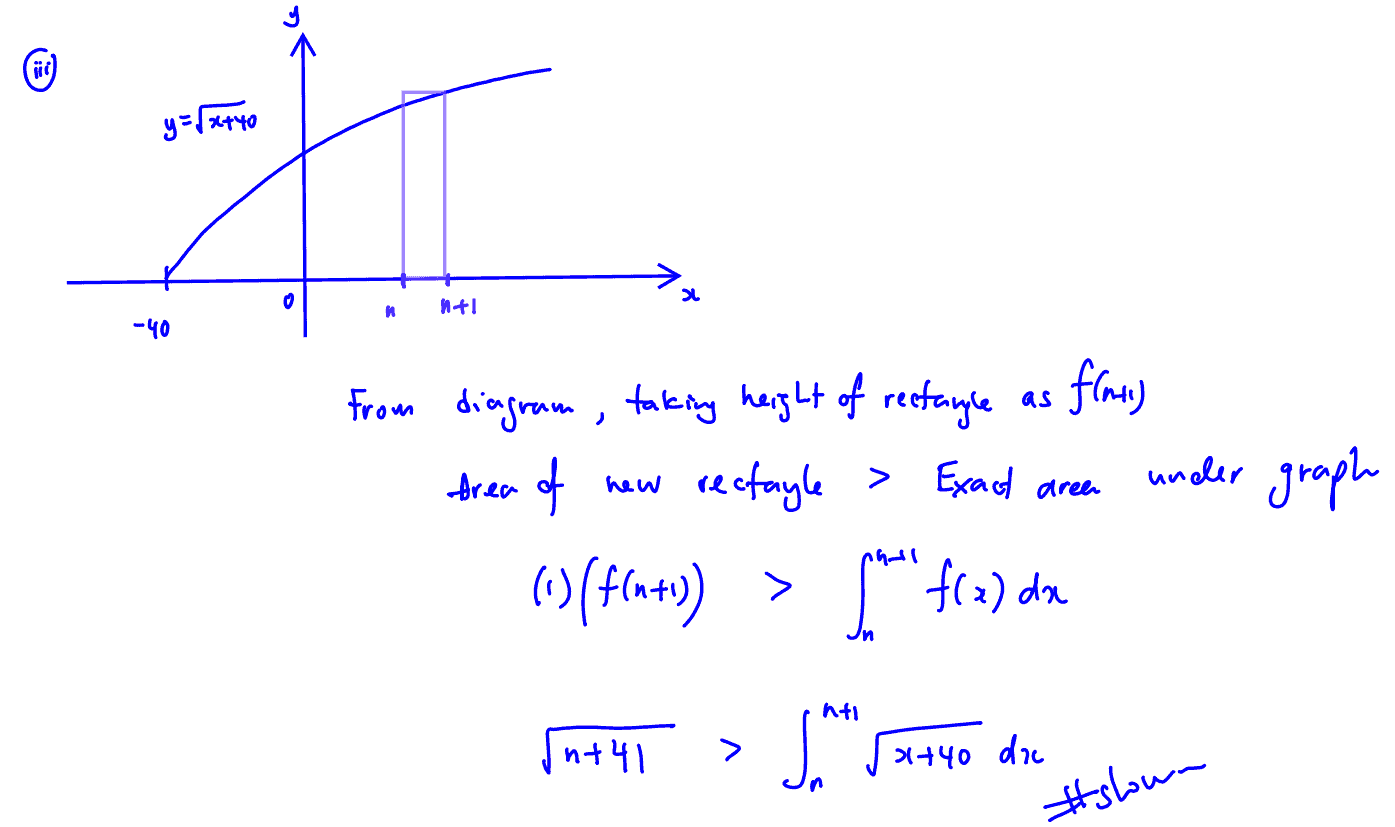
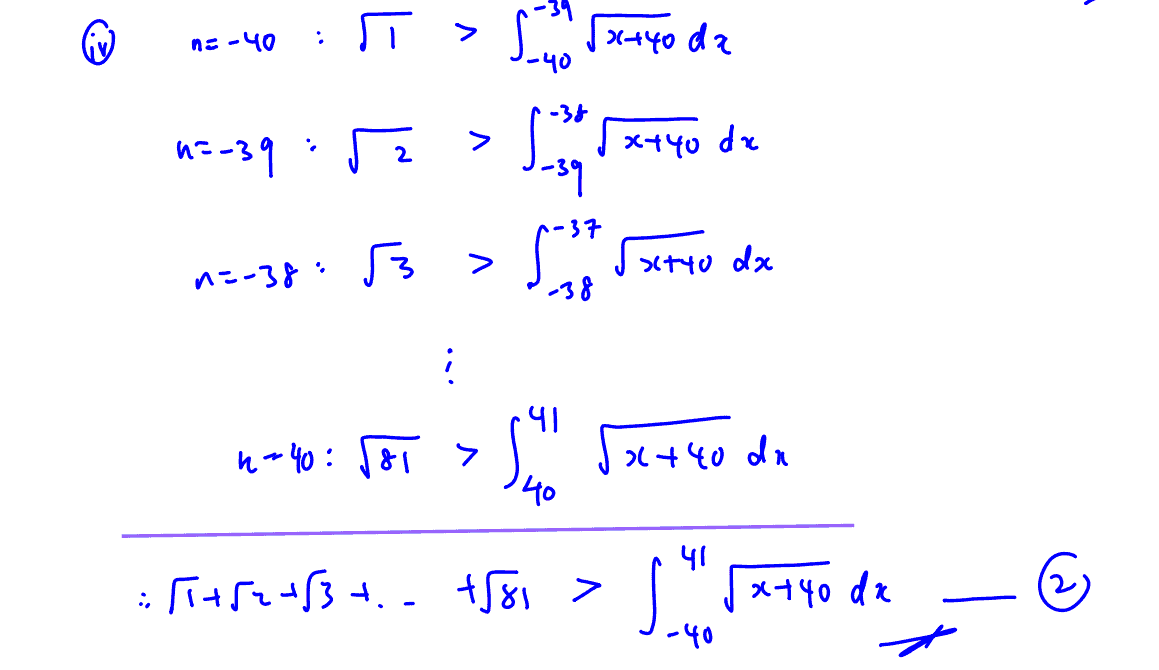
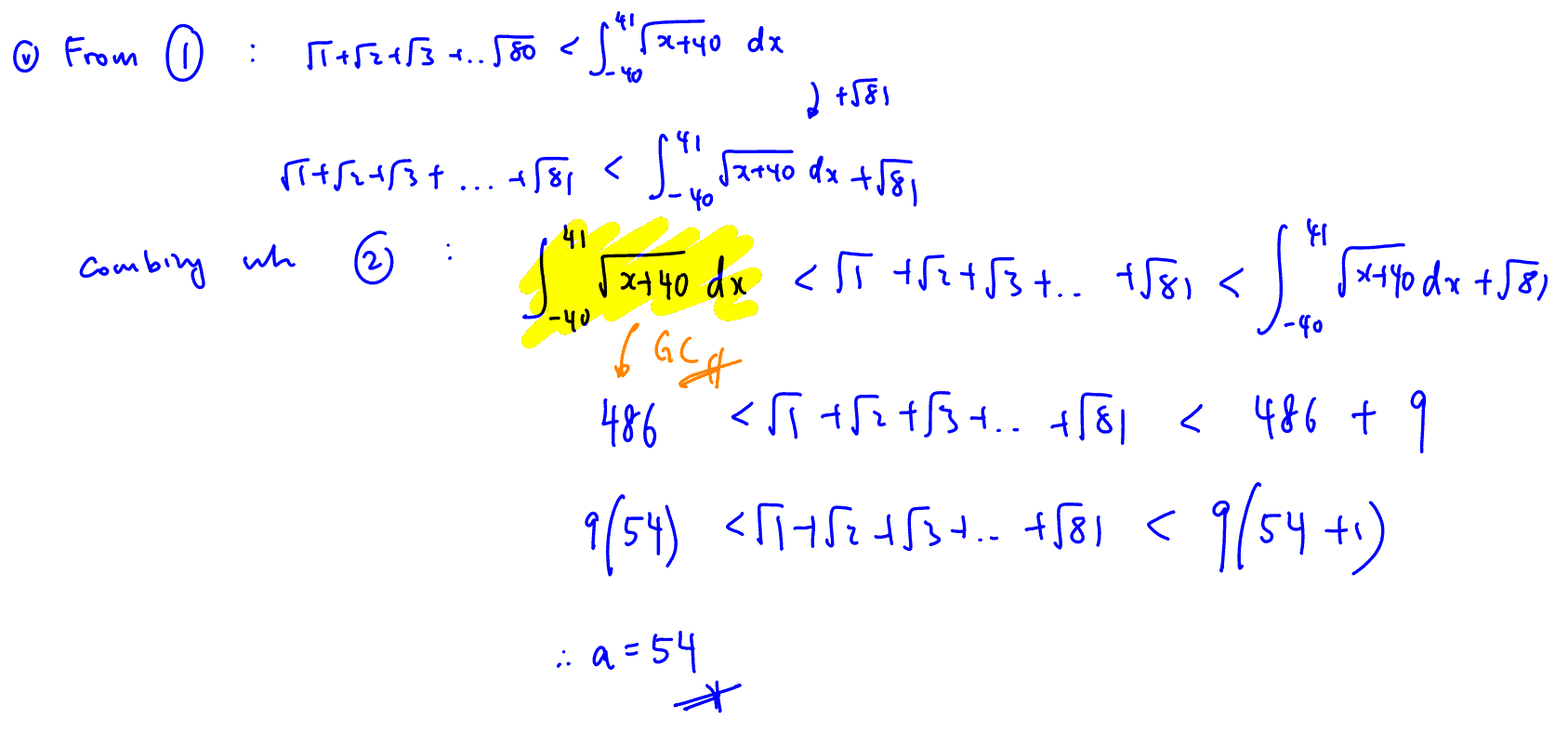
- (i)
- (ii)
- (iii)
- (iv)
- (v)
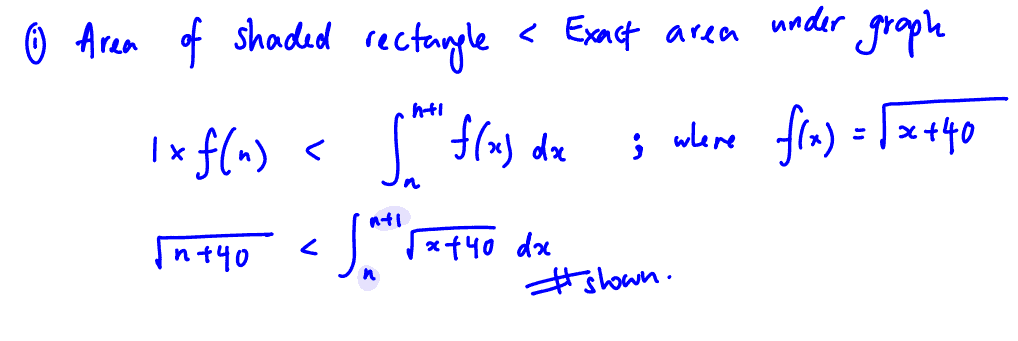

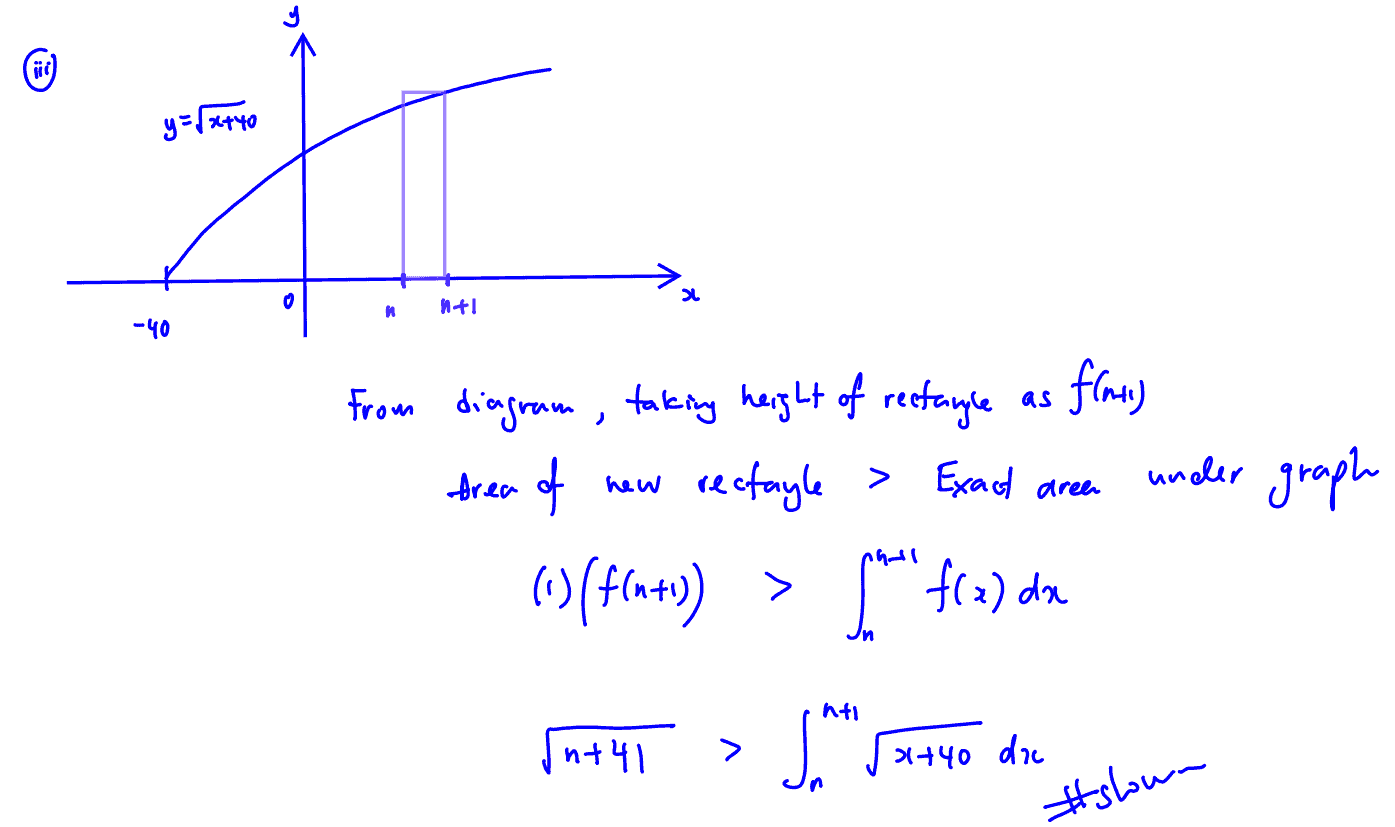
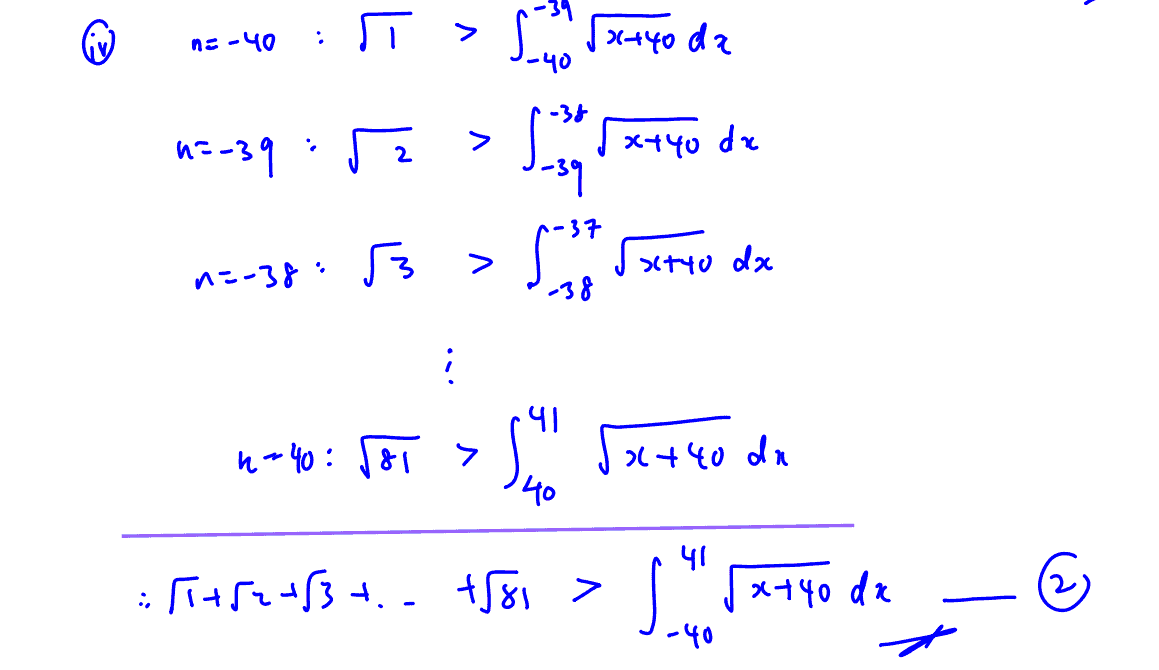
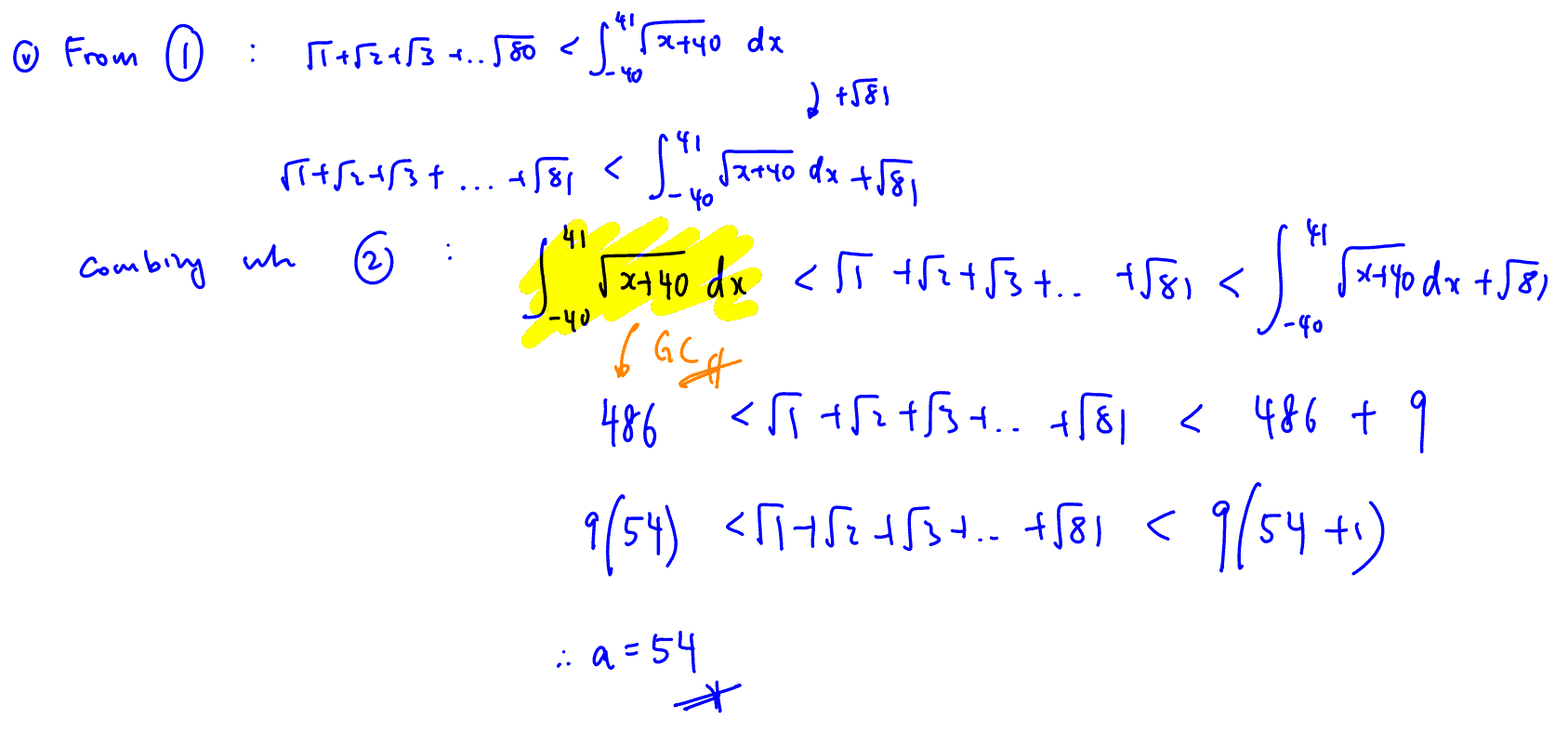
Share with your friends!
Download Techniques of Integration Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!