A-Level H2 Math | 5 Essential Questions
Transformations of Graphs
Transformation, in mathematics, is a change in the form of a mathematical object without changing the underlying properties of that object. We can perform a transformation on an object by moving it from one place to another on the coordinate plane according to some rules. There are four types of transformations, namely translation, reflection, dilation, and rotation.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2021 NJC Lecture Test (b)
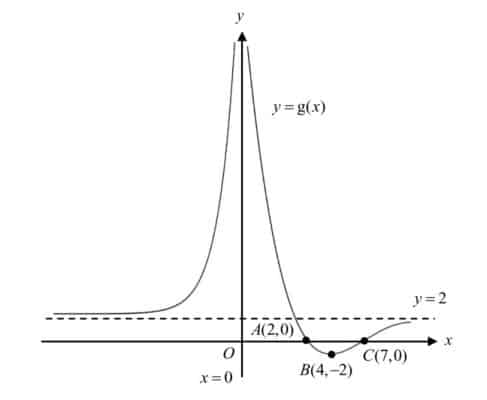
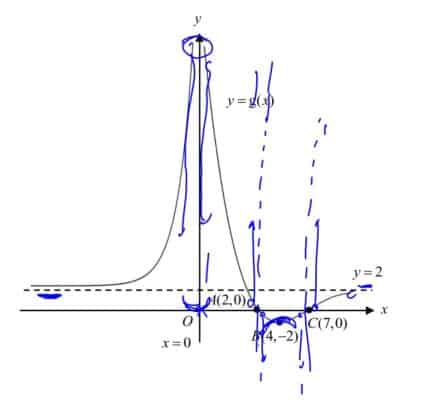
The diagram below shows a sketch of the curve with equation $y=\text{g}(x)$. The curve has asymptotes with equations$x=0$ and $y=2$. The curve crosses the $x$-axis at $A(2,0)$ and $C(7,0)$ and has a turning point at $B(4,-2)$.
On separate diagrams, sketch the curves with equations
(i)
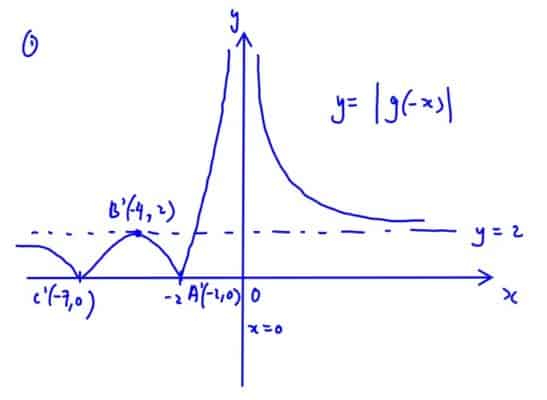
$y=\left| \text{g}(-x) \right|$,
[3]
(i) $y=\left| \text{g}(-x) \right|$,
[3]
(ii)
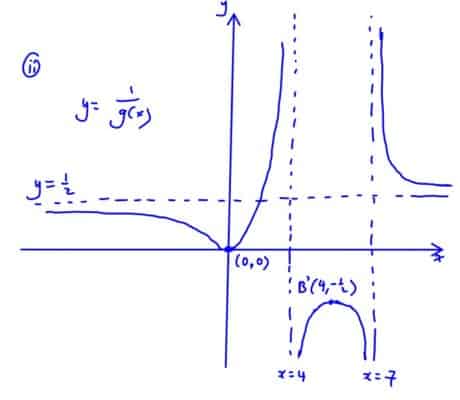
$y=\frac{1}{\text{g}(x)}$.
[4]
(ii) $y=\frac{1}{\text{g}(x)}$.
[4]
For each curve, state clearly the equations of any asymptotes, the coordinates of any turning points and the coordinates of any points where the curves crosses the $x$- and $y$- axes.
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (i)
- (ii)



Share with your friends!
ACJC Tutorial 3 Q9
A graph with the equation $y=\text{f}(x)$ undergoes, in succession, the following transformations:
$A$: A translation of $1$ unit in the direction of the positive $x$- axis.
$B$: A stretch parallel to the $x$- axis by factor $\frac{1}{2}$.
$C$: A reflection in the $y$- axis.
The equation of the resulting curve is $y=\frac{2}{2{{x}^{2}}+2x+1}$. Determine the equation $y=\text{f}(x)$.
Suggested Handwritten and Video Solutions


Share with your friends!
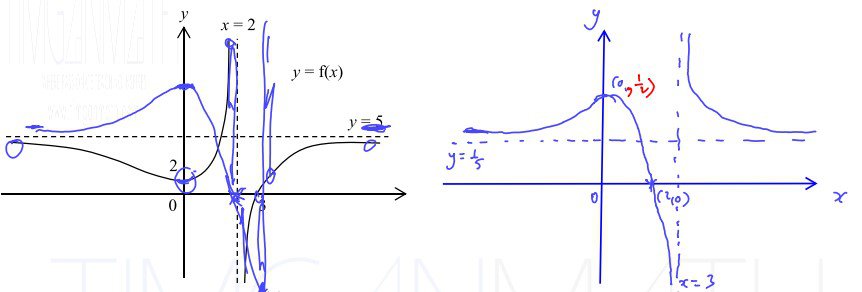
2013 VJC P1 Q6 (i)
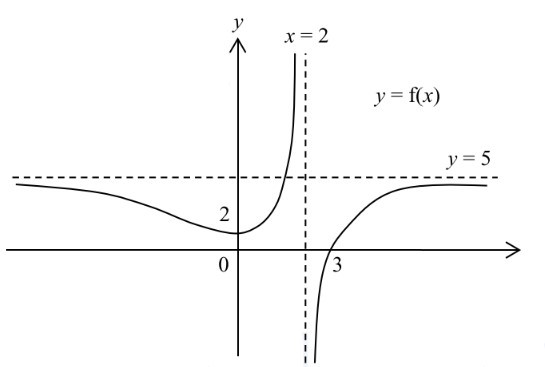
The diagram shows the graph of $y=\text{f}(x)$ which has a minimum point at $(0, 2)$ and asymptotes $x=2$ and $y=5.$
On separate diagrams, sketch the graphs of $y\ =\ \ \frac{1}{\text{f}(x)}$.
Suggested Handwritten and Video Solutions
Share with your friends!
2020 VJC Promo Q8
(a)
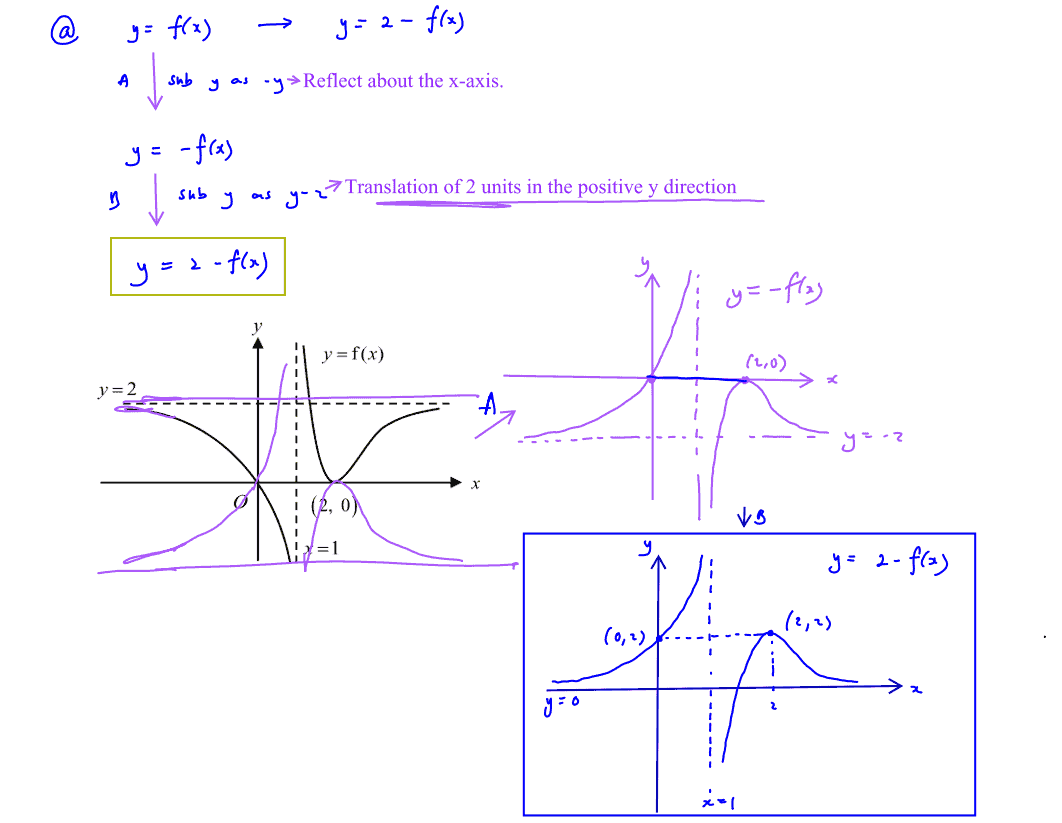
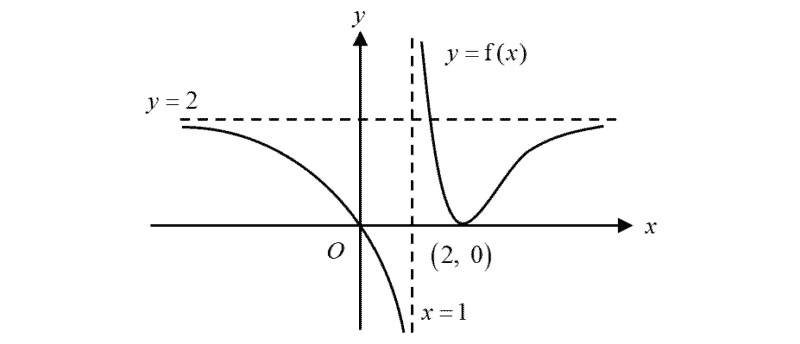 Sketch the graph of $y=2-\text{f}(x)$, stating the coordinates of the point where the graph crosses the $y$-axis, the coordinates of any stationary point(s) and the equations of any asymptotes.
Sketch the graph of $y=2-\text{f}(x)$, stating the coordinates of the point where the graph crosses the $y$-axis, the coordinates of any stationary point(s) and the equations of any asymptotes.
[2]
(a) The graph of $y=\text{f}(x)$ is shown in the diagram. It passes through the origin and has a minimum point at $\left( 2,\text{ }0 \right)$. The lines $x=1$ and $y=2$ are the asymptotes of the graph.
[2]
(b)
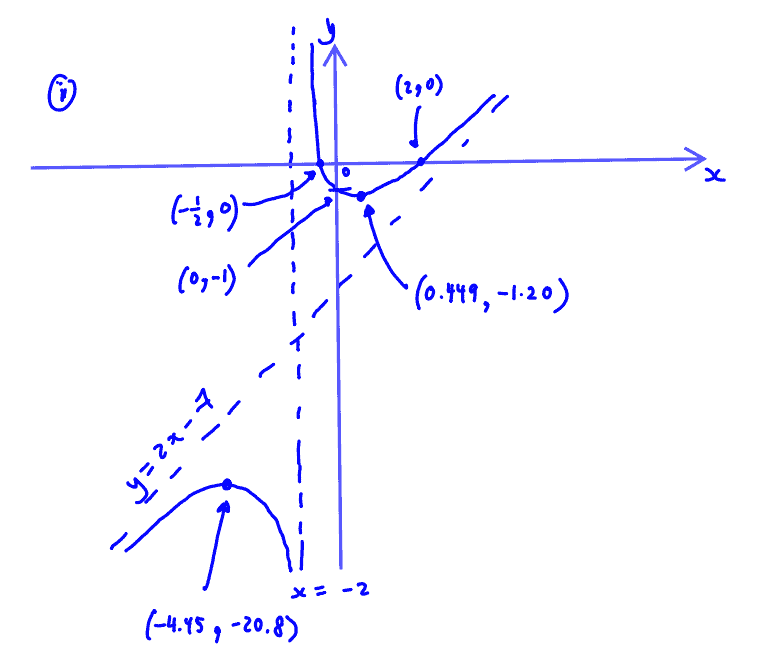
The curve $C$ has equation $y=\frac{2{{x}^{2}}+kx-2}{x+2}$, where $k$ is a constant.
(i)
Find the set of values of $k$ for which $C$ has $2$ stationary points.
[3]
[3]
For the rest of the question, take $k=-3$.
For the rest of the question, take $k=-3$.
(ii)
By expressing the equation $y=\frac{2{{x}^{2}}-3x-2}{x+2}$ in the form $y=ax+b+\frac{c}{x+2}$, where $a$, $b$ and $c$ are constants, write down the equations of the asymptotes of $C$.
[3]
(ii) By expressing the equation $y=\frac{2{{x}^{2}}-3x-2}{x+2}$ in the form $y=ax+b+\frac{c}{x+2}$, where $a$, $b$ and $c$ are constants, write down the equations of the asymptotes of $C$.
[3]
(iii)
Hence sketch $C$, giving the equations of any asymptotes, the coordinates of any stationary points and of the points where $C$ crosses the axes.
[2]
(iii) Hence sketch $C$, giving the equations of any asymptotes, the coordinates of any stationary points and of the points where $C$ crosses the axes.
[2]
(iv)
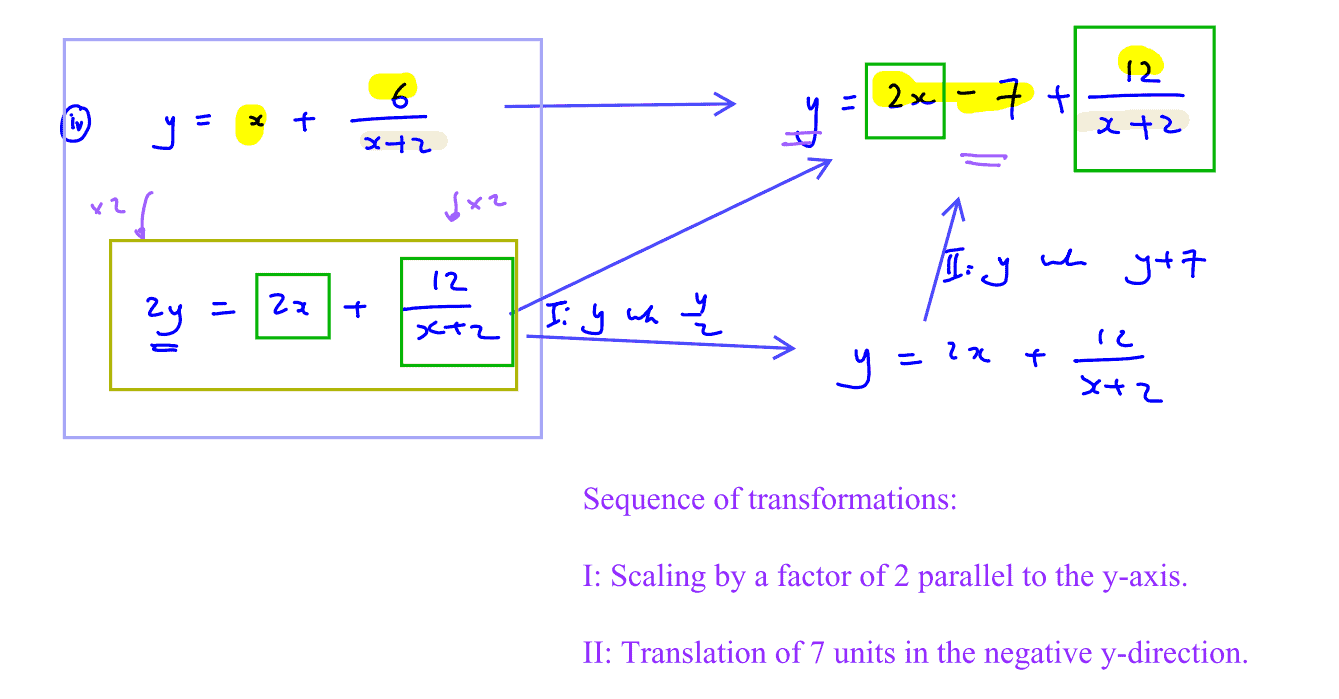
Describe a pair of transformations which transform the graph of $y=x+\frac{6}{x+2}$ to $C$.
[2]
(iv) Describe a pair of transformations which transform the graph of $y=x+\frac{6}{x+2}$ to $C$.
[2]
Suggested Handwritten and Video Solutions
- (a)
- (b)(i)
- (b)(ii)
- (b)(iii)
- (b)(iv)
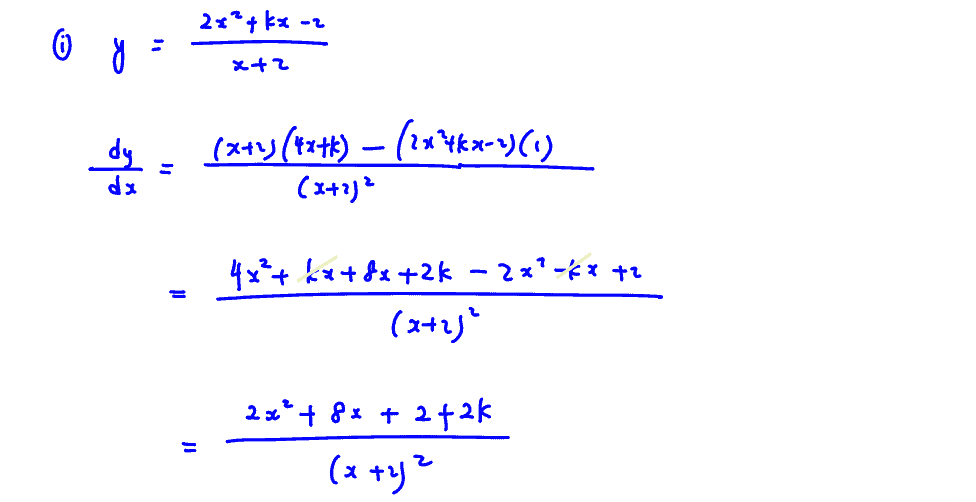
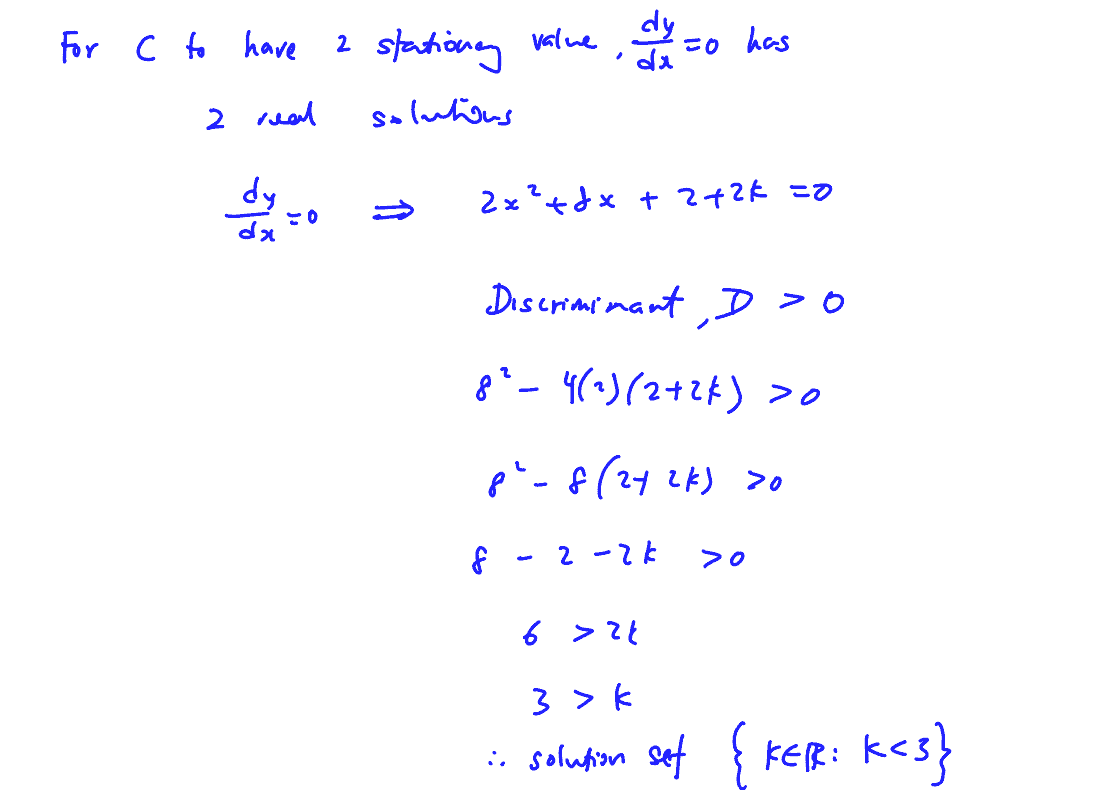
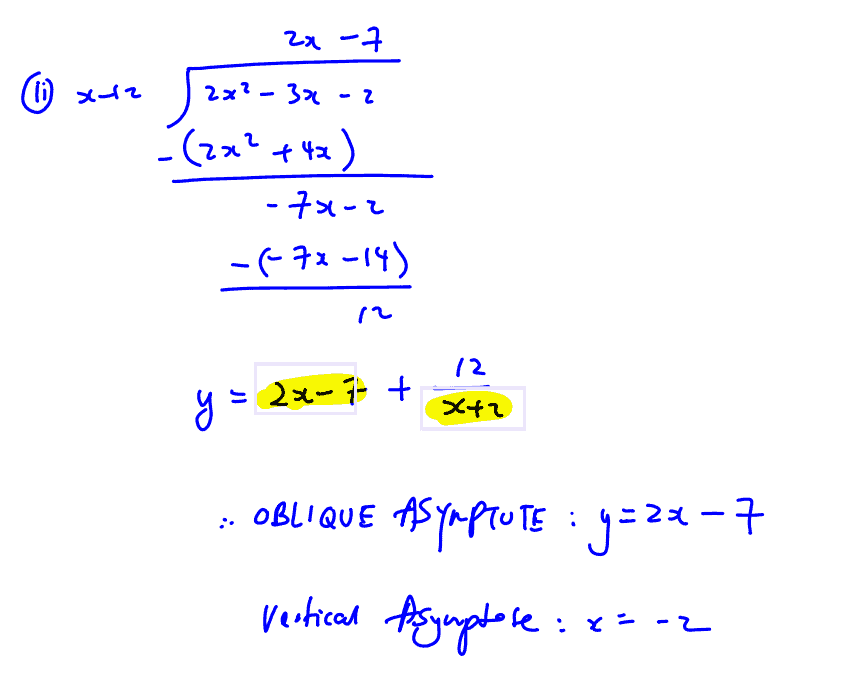
- (a)
- (b)(i)
- (b)(ii)
- (b)(iii)
- (b)(iv)

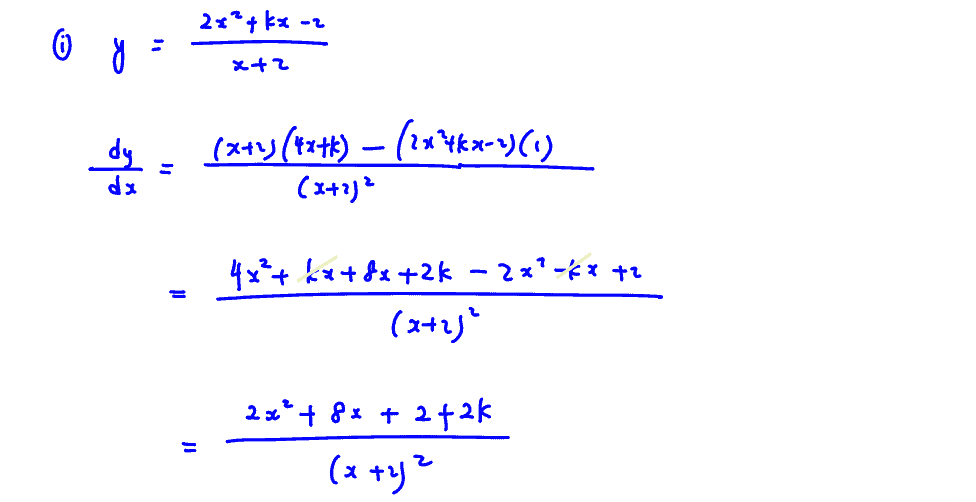
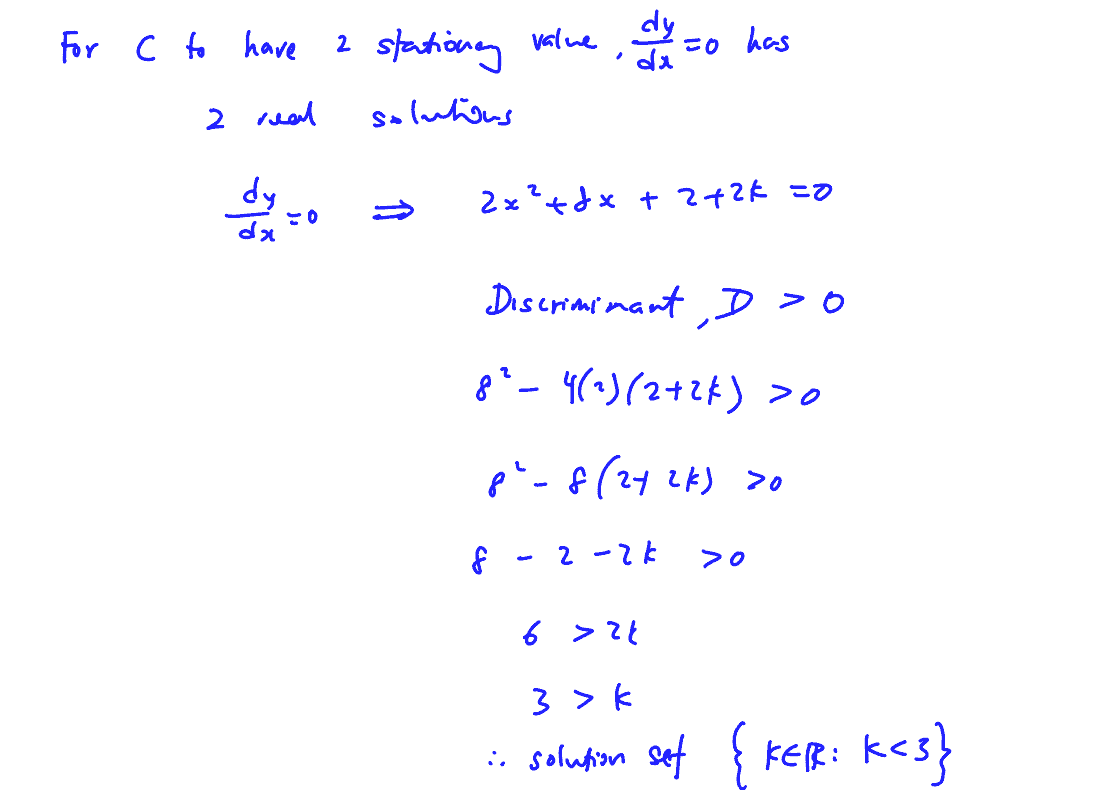
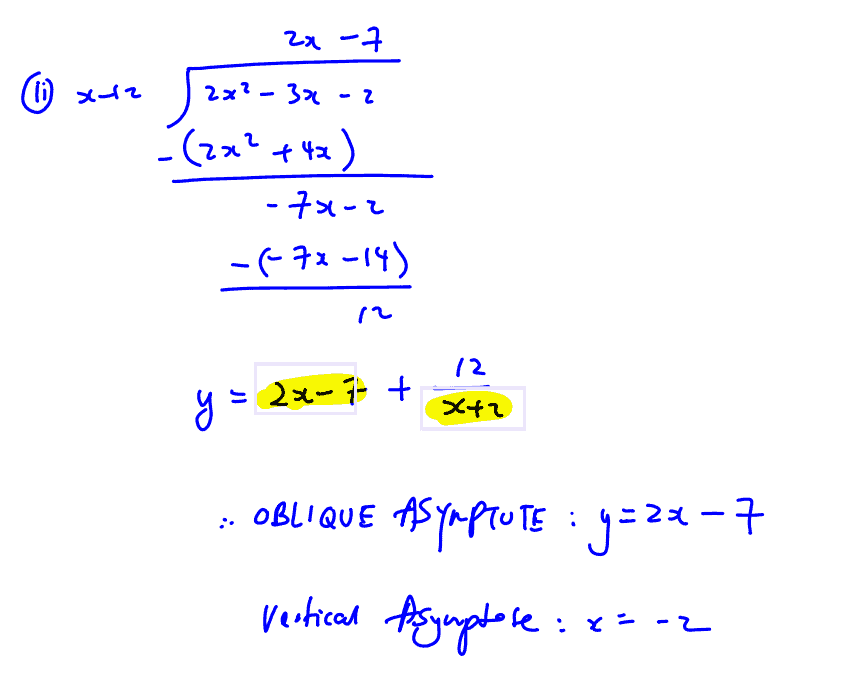


Share with your friends!
2019 RI P1 Q5
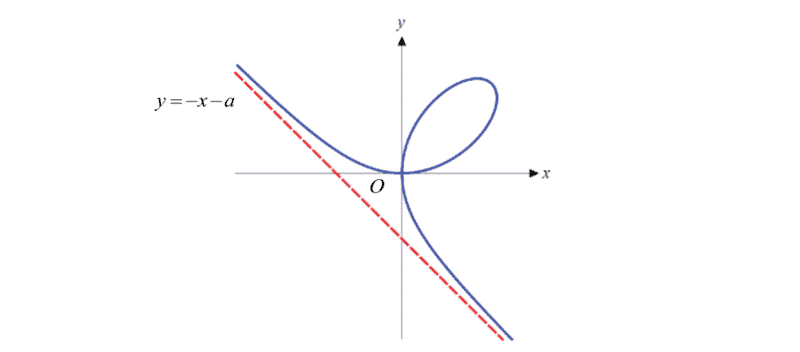
The diagram shows the graph of Folium of Descartes with cartesian equation
${{x}^{3}}+{{y}^{3}}=3axy$,
where a is a positive constant. The curve passes through the origin, and has an oblique asymptote with equation $y=-x-a$.
(i)
Given that $\left( 0,0 \right)$ is a stationary point on the curve, find, in terms of a, the coordinates of the other stationary point.
[5]
(i) Given that $\left( 0,0 \right)$ is a stationary point on the curve, find, in terms of a, the coordinates of the other stationary point.
[5]
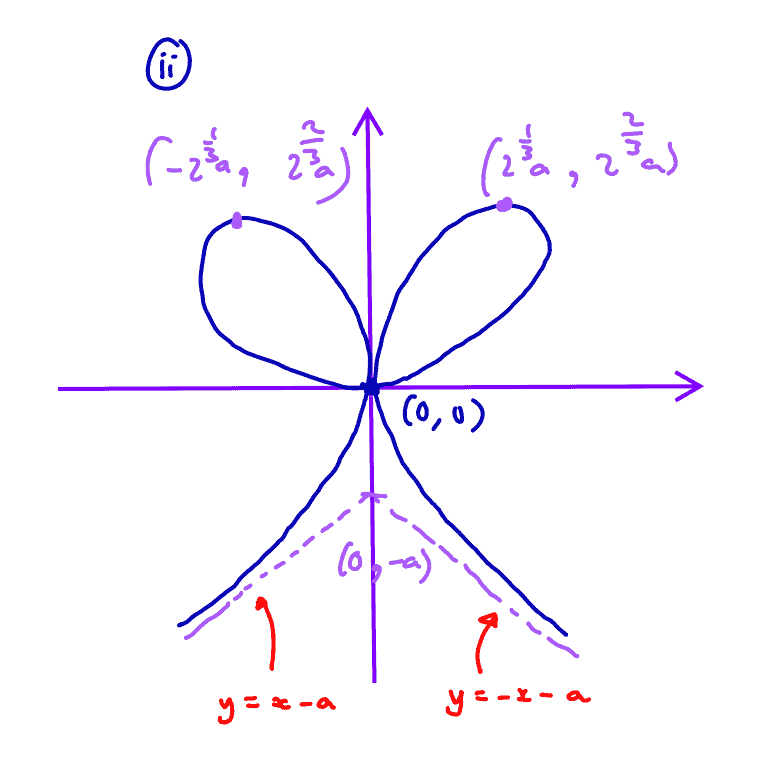
(ii)
Sketch the graph of
${{\left| x \right|}^{3}}+{{y}^{3}}=3a\left| x \right|y$,
including the equations of any asymptotes, coordinates of the stationary points and the point where the graph crosses the $x$-axis.
[3]
(ii) Sketch the graph of
${{\left| x \right|}^{3}}+{{y}^{3}}=3a\left| x \right|y$,
including the equations of any asymptotes, coordinates of the stationary points and the point where the graph crosses the $x$-axis.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)

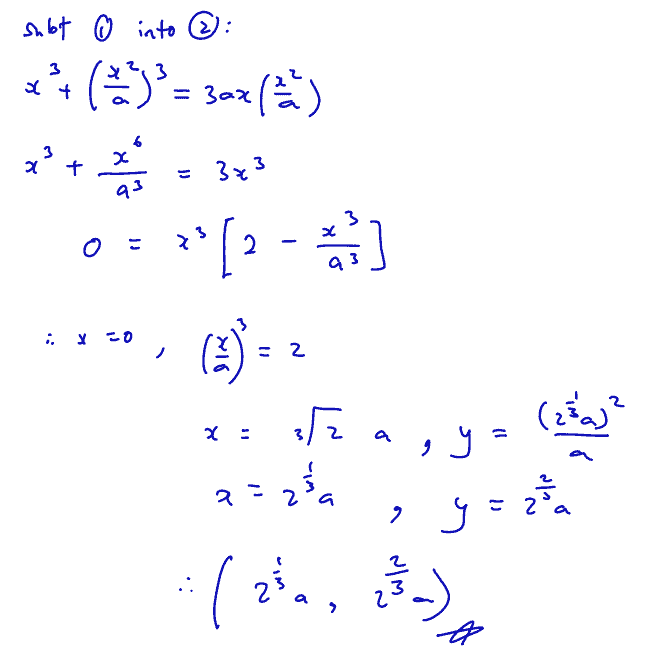
- (i)
- (ii)

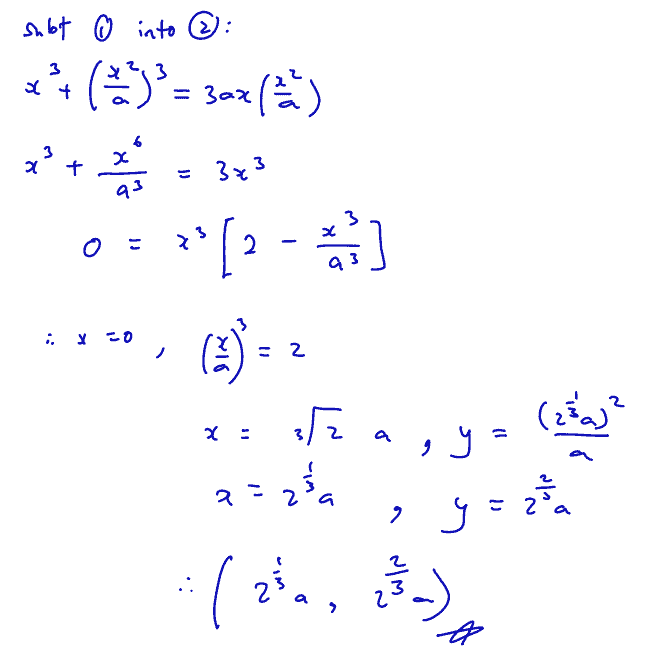

Share with your friends!
Download Transformations of Graphs Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!