Timothy Gan
- Why (a + b)² ≠ a² + b² ?
- Why a² − b² = (a+b)(a−b)?
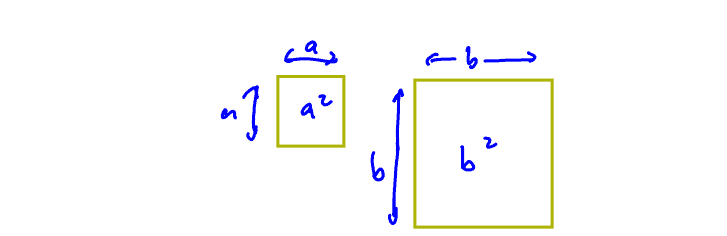
This is probably one of the most common mathematics mistakes we have done at least once in our life, which is (a+b)² = a²+b². Now what we need to understand is why is this not the case. Now before we start, we just have to understand the idea of a square. The concept of a square is pretty simple. Say if we want a², a² just means that we have a square of sides a. Thus, the area is multiplied by a. So, similarly for b².
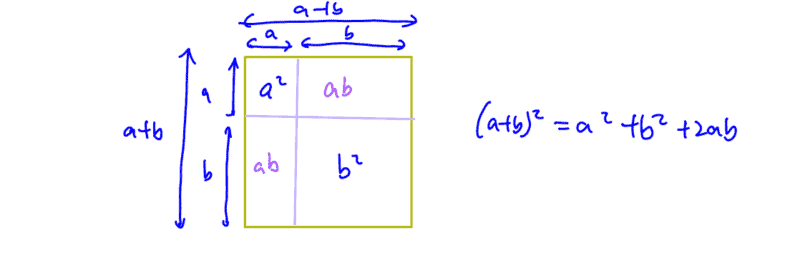
What we need to understand is the length of this side here is b and this side here is b and hence the area here is b². So what does (a+b)² mean? This would mean that we have a huge square. Now in this case here, we’re going to split one side into a and b and this side into a and b. This means that we have a side of a and this side will be b.
The whole side will just be a+b. And this will give us what we are looking for, which is an (a+b)². So in this case here, if you look at the big square here, we know that if we expand in this form [(a + b)² = a² + b²] we’re actually missing out on something (Hint: purple colour in the diagram), right?
The area which we did not account for when we wrote such a common mistake is actually ab-ab right? So in other words, to fix the expansion, we need to just put 2ab in to get the correct expansion:
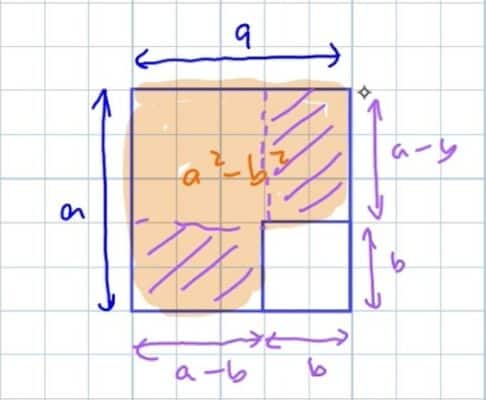
Let’s explore why a² − b² = (a + b)(a − b) by using the diagram here.
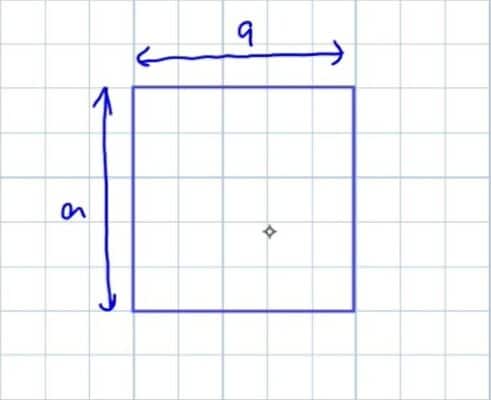
So what does a² − b² mean?
a² just means that if I have a square of sides a, the area will be a².
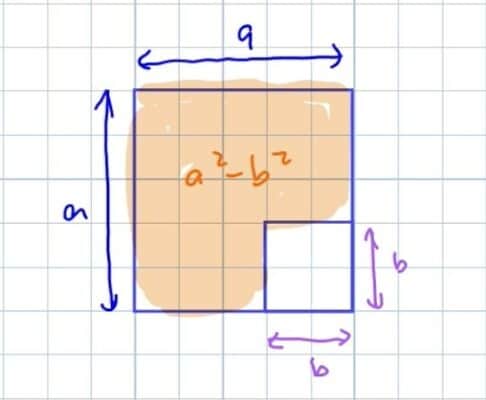
Remove away b² would then just mean that we take away a b² here.
A length of b and a length of b shouldn’t be so surprising, that this area here that we’re looking that is our a² – b².
Now what we need to do is to split them up and rearrange this area here.
From here, what we can see is if we were to split them into smaller rectangles, the length would be a – b.
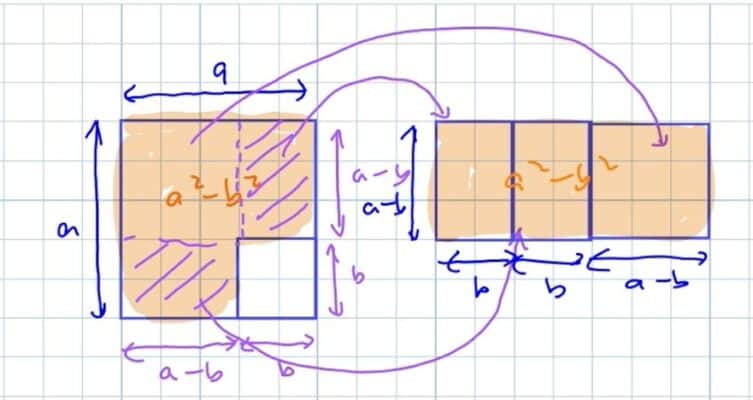
What we’re going to do is just rearrange this rectangle over here.
Bring the two rectangles over, and we would be able to move the square over to this side here in this form.
The height of the new rectangle here is a – b.
And the length would be b + b + a – b = a + b.
From here we know that the area here would be a² – b² because we are using the highlighted area in the first figure to form the new rectangle here.
The area of a² – b² would be the length multiplied by the height of the new rectangle.
That will give us a + b multiplied by a – b.
Hence a² − b² = (a + b) (a – b).