- Home
- Study Guides
Trigonometric Curves
The sine, cosine and tangent graphs serve as an introduction to trigonometry, which is one of the most fundamental topics in mathematics. The graphs are a visual representation of trigonometry and show the relationship between sine, cosine and tangent functions. This relationship is used by trigonometric formulas to solve real-world problems.
Sketching of Sine Curves
The sine curve is an example of a periodic function and it can be plotted on the complex plane or in the $xy$-plane. It is also called a sine wave or sinusoidal curve. The basic characteristic of this curve is that it repeats itself every $2\pi$ radians, or $360^\circ $. Sine curve can be used to determine velocity, acceleration, and displacement through the use of trigonometry.
Quiz 1
The graph below shows the curve $y=\sin x$:
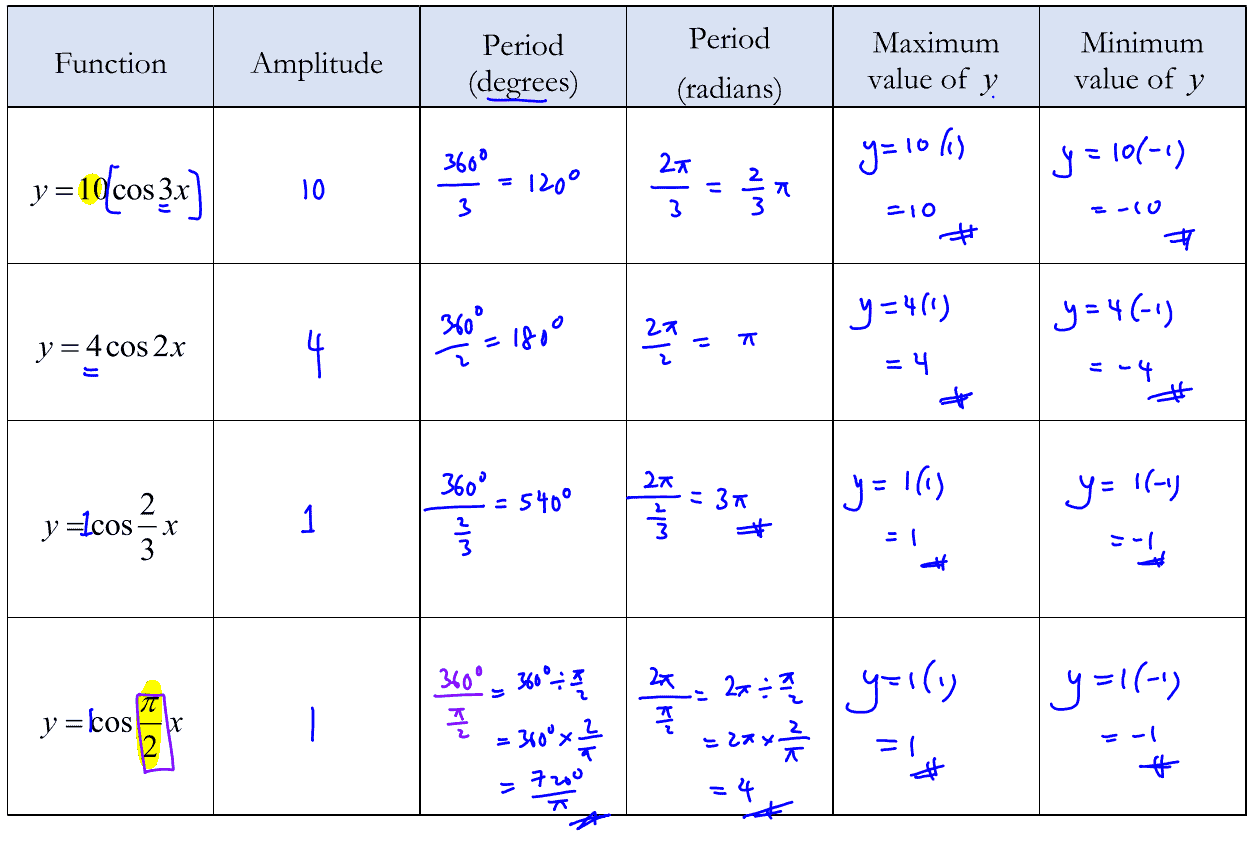
Properties of $y=\sin x$
Amplitude $=1$
Period, $T=2\pi $ or $360^\circ $
Max value of $\sin (x)=1$
Min value of $\sin (x)=-1$
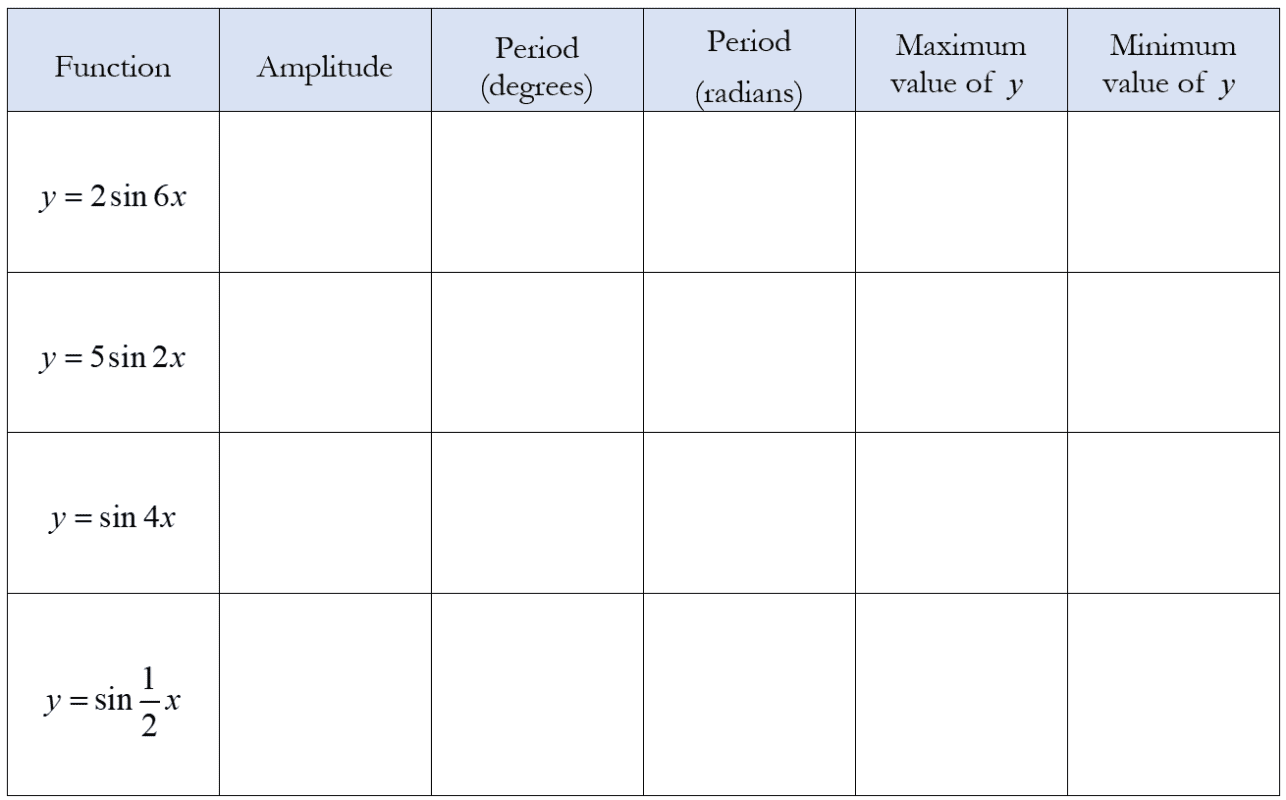
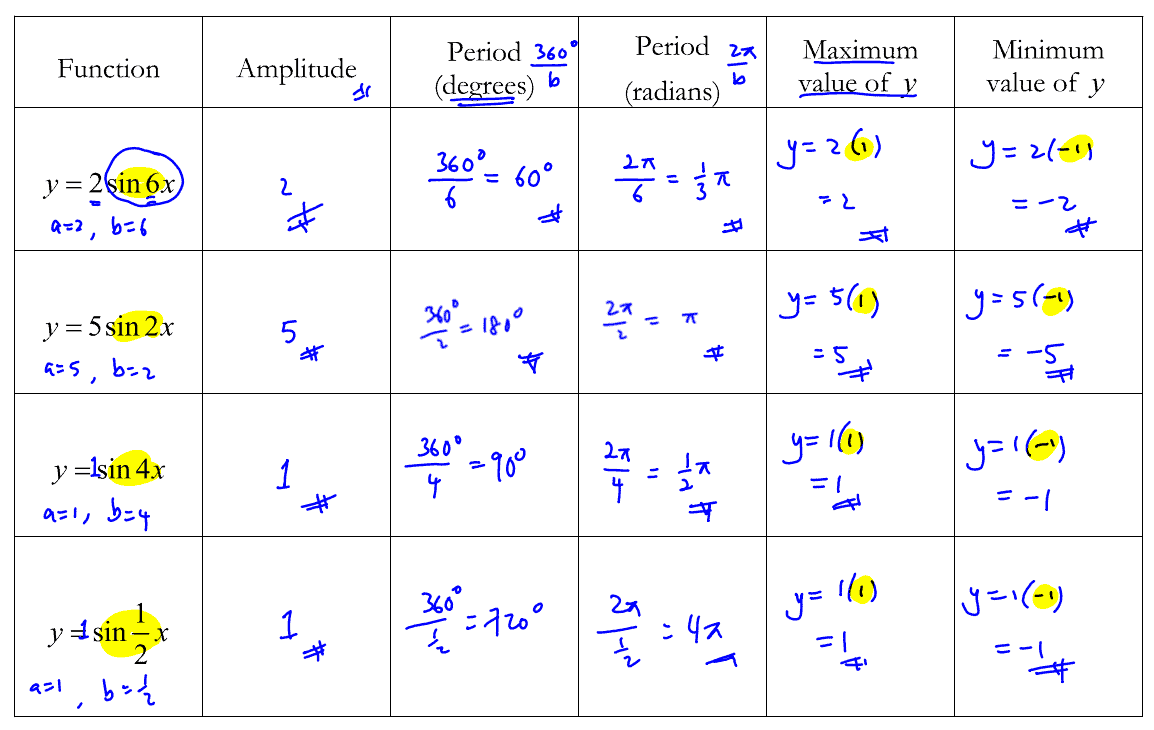
Properties of $y=a\sin (bx), a>0$
So if we sketch a sine graph with increasing amplitude $(a=2)$ and $(a=3)$, it will look like this:
Figure A: $y=2\sin x$
Figure B: $y=3\sin x$
One way to control the shape of a sinusoidal wave is to alter its amplitude. A wave’s amplitude is a number measuring how high it gets, and what determines its maximum height is the maximum value of its $y$-coordinate. The next question is: what happens if we increase the value of $a$?
From the previous figure, we can see that the amplitude ($a$) of the sine curve is constant. When the amplitude of a sine curve increases by one, the height of the wave also increases by one. This is called vertical shift. Increasing the amplitude will make the sine curve steeper and we will end up with a graph twice as big.
The amplitude becomes $a$.
When we sketch a sine graph with variable $(b=2)$ and $(b=3)$, the graphs will look like this:
Figure A: $y=\sin 2x$
Figure B: $y=\sin 3x$
Another way to manipulate the shape of a sinusoidal wave is to change the period. The period of a trigonometry function is the extent to which the function runs through all possible values before reaching its original value and starting over again. What if we make the angle variable $(x)$ bigger by multiplying the angle variable with a number $(b)$?
The variable $b$ tells us the number of cycles between $0$ and $2\pi $. Increasing the variable $b$ will result in a higher frequency, also known as the number of complete cycles, in the period.
In this case, the period is being reduced and hence, the formula for the period is $T=\frac{2\pi }{b}$ or $\frac{360^ \circ}{b}$.
To summarize, the properties of $y=a\sin (bx), a>0$ are
Amplitude $=a$
Period, $T=\frac{2\pi }{b}$ or $\frac{360^ \circ}{b}$
Max value of $\sin (bx)= 1$
Min value of $\sin (bx)= -1$
Practice Question 1
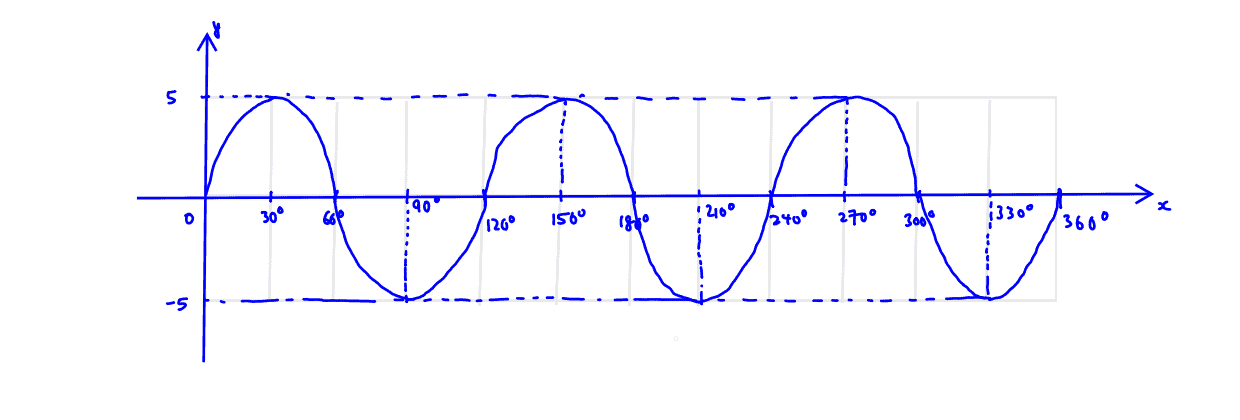
Sketch the graph $y=5\sin3x$ for $0\le x\le 360^\circ$, stating the amplitude and period.
Period$=\frac{360{}^\circ }{3}=120{}^\circ ,a=5$
No. of cycles$=\frac{360^\circ}{120^\circ}=3$
Click to enlarge image
Sketching of Cosine Curves
The cosine graph is a sine graph shifted by $90$ degrees so that it corresponds to the cosine function. The cosine curve starts at $1$.
Quiz 2
Click to enlarge image
The graph below shows the cosine curve, $y=\cos x$.
Properties of $y=\cos x$
Amplitude $=1$
Period, $T=2\pi $ or $360^\circ $
Max value of $\sin (x)=1$
Min value of $\sin (x)=-1$
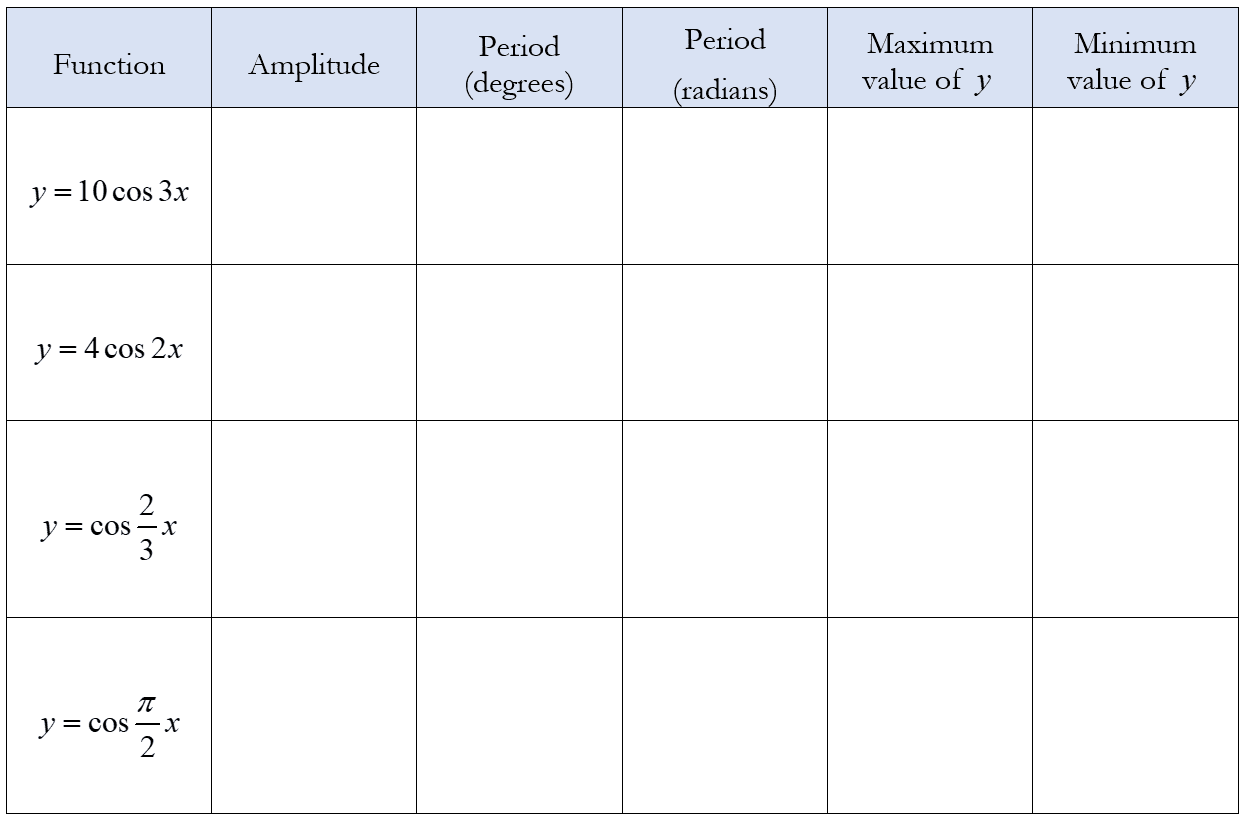
Properties of $y=a\cos (bx),a>0$
Similarly, the height of the curve corresponds directly to the amplitude of a cosine curve.
The figure on the left show the cosine graphs with amplitude $(a=2)$ and $(a=3)$.
Figure A: $y=2\cos x$
Figure B: $y=3\cos x$
Likewise, the frequency of the complete cycle in the period also increases correspondingly when we increase the variable $b$.
The figure on the left show the cosine graphs with $b=2$ and $b=3$.
Figure A: $y=\cos 2x$
Figure B: $y=\cos 3x$
To recap, the properties of $y=a\cos (bx),a>0$ are:
Amplitude $=a$
Period, $T=\frac{2\pi }{b}$ or $\frac{360^ \circ}{b}$
Max value of $\sin (bx)= 1$
Min value of $\sin (bx)= -1$
Steps of Sketching Sine and Cosine Curve
- Decide the number of complete cycles required. No. of cycles$=\frac{\text{Given Domain}}{\text{Period}}$.
- Draw the grids out based on the number of complete cycles required. Take note that we need $4$ grids per cycle.
- Sketch the curve on the grid.
- Draw the $y$-axis.
- Mark down the Amplitude and the Period.
- Finally, draw the $x$-axis with respect to the line of equilibrium.
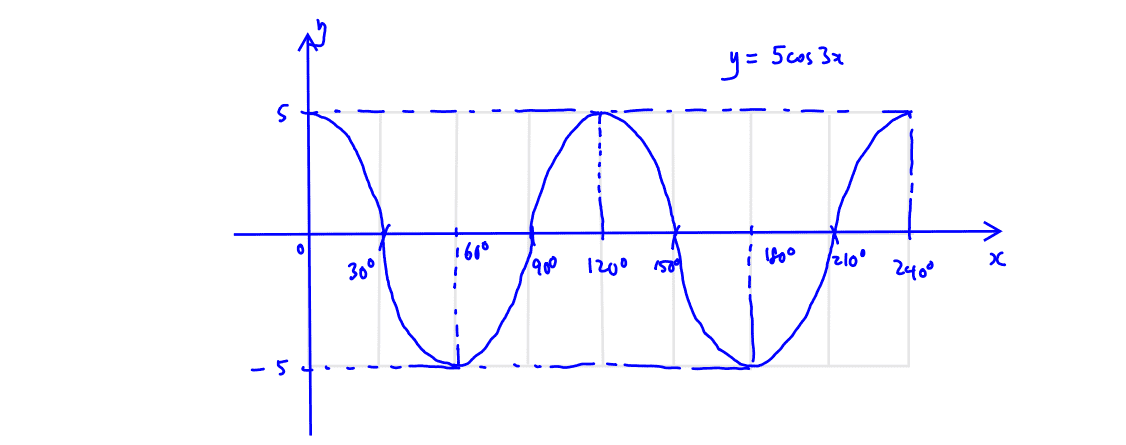
Practice Question 2
Sketch the graph of $y=5\cos 3x$ for $0 \le x \le 240^\circ$, stating the amplitude and period.
Period$=\frac{360{}^\circ }{3}=120{}^\circ ,a=5$
No. of cycles$=\frac{240^\circ}{120^\circ}=2$
Click to enlarge image
Sketching of Tangent Curves
From the sine and cosine curves, we know that the graph of a trigonometric function has an amplitude. The tangent curve, however, has no amplitude because the function is undefined. There is a line in the graph where the curve will never touch – the asymptote. Since the function approach to infinity at the asymptote, there is no maximum or minimum value.
Quiz 3
Click to enlarge image
The graph below shows the tangent curve, $y=\tan x$.
Properties of $y=\tan x$
Period, $T=\pi$ or $180^\circ $
Note: The period of the tangent curve is $\pi$ or $180^\circ $ which is different from that of the sine and cosine curve.
Properties of $y=a\tan (bx),a>0$
Period, $T=\frac{\pi}{b}$ or $\frac{180^\circ}{b}$
Figure A: $y=\tan 2x$
Figure B: $y=\tan 3x$
Steps of Sketching Tangent Curve
- Decide the number of complete cycles required. No. of cycles$=\frac{\text{Given Domain}}{\text{Period}}$.
- Draw the grids out based on the number of complete cycles required. Take note that we need $2$ grids per cycle.
- Draw the $y$ and $x$ axes.
- Draw the asymptotes on grid lines $1,3,5,7,…$.
- Sketch the curve.
- Mark down the period and label the graph.
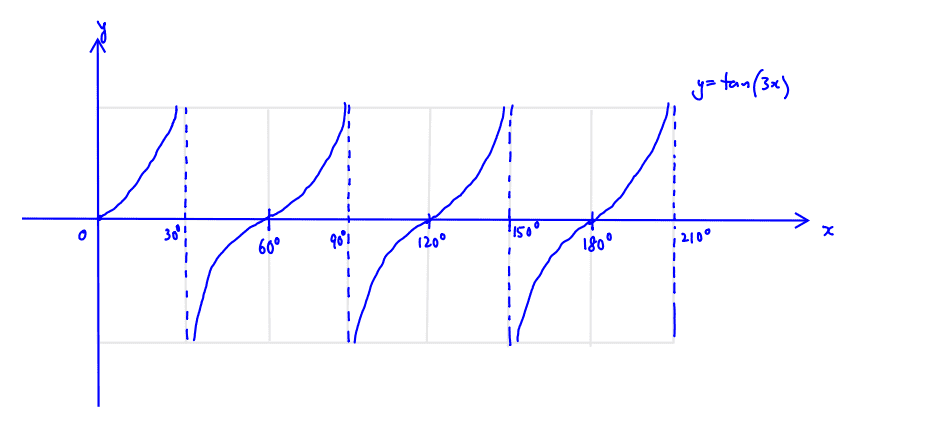
Practice Question 3
Sketch the graph of $y=\tan (3x)$ for $0^\circ \le x \le 210^\circ$. State the period of the function.
Period$=\frac{180{}^\circ }{3}=60{}^\circ $
No. of cycles$=\frac{210^\circ}{60^\circ}=\frac{7}{2}=3.5$
Click to enlarge image
Sketching of Translated Curves
The sine and cosine curves can be translated in any of four directions: left, right, up, and down just like any other function. How do we identify the shift?
- If the addition or subtraction happens after the sine and cosine functions, the function translates vertically.
- If the addition or subtraction happens before the sine and cosine functions, the function translates horizontally.
In this article, we will focus on the vertical translation:
- The function shifts upwards when addition happens after the function.
- The function shifts downwards when subtraction happens after the function.
Properties of $y=a\sin (bx)+c,a>0$:
Amplitude $=a$
Period, $T=\frac{2\pi }{b}$ or $\frac{360^ \circ}{b}$
Max value of $a\sin (bx)+c= a+c$ when $a>0$
Min value of $a\sin (bx)+c= -a+c$ when $a>0$
Figure A: $y=\sin x$
Figure B: $y=2\sin x$
Figure C: $y=\sin 2x$
Properties of $y=a\cos (bx)+c,a>0$:
Amplitude $=a$
Period, $T=\frac{2\pi }{b}$ or $\frac{360^ \circ}{b}$
Max value of $a\cos (bx)+c= a+c$ when $a>0$
Min value of $a\cos (bx)+c=-a+c$ when $a>0$
Figure A: $y=\cos x$
Figure B: $y=2\cos x$
Figure C: $y=\cos 2x$
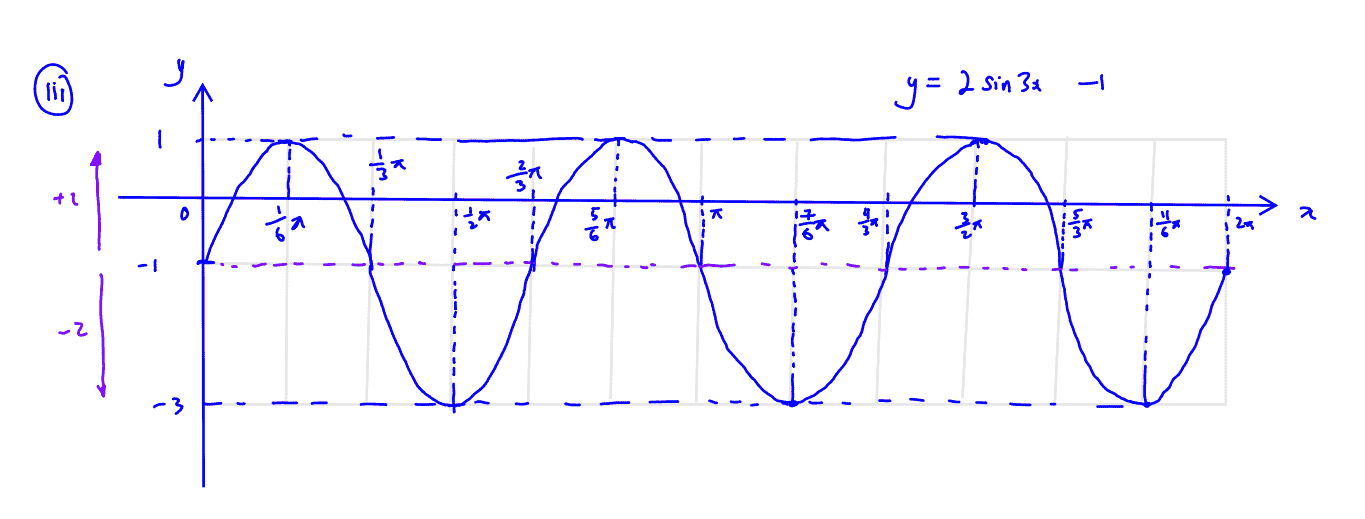
Practice Question 4
The equation of a curve is $y=2\sin 3x-1$ for $0 \le x \le 2\pi$.
(i)
Write down the maximum and minimum values of $y$.
(i) Write down the maximum and minimum values of $y$.
(ii)
State the amplitude, the period and the range of the function.
(ii) State the amplitude, the period and the range of the function.
(iii)
Hence, sketch the graph of $y$.
(iii) Hence, sketch the graph of $y$.
Maximum of $y=2(1)-1=1$
Minimum of $y=2(-1)-1=-3$
Amplitude $=2$
Period $=\frac{2\pi}{3}$
Range $=-3 \le y \le 1$
No. of cycles $=\frac{2\pi}{\frac{2\pi}{3}}=3$ cycles
Click to enlarge image
Maximum of $y=2(1)-1=1$
Minimum of $y=2(-1)-1=-3$
Amplitude $=2$
Period $=\frac{2\pi}{3}$
Range $=-3 \le y \le 1$
No. of cycles $=\frac{2\pi}{\frac{2\pi}{3}}=3$ cycles
Click to enlarge image
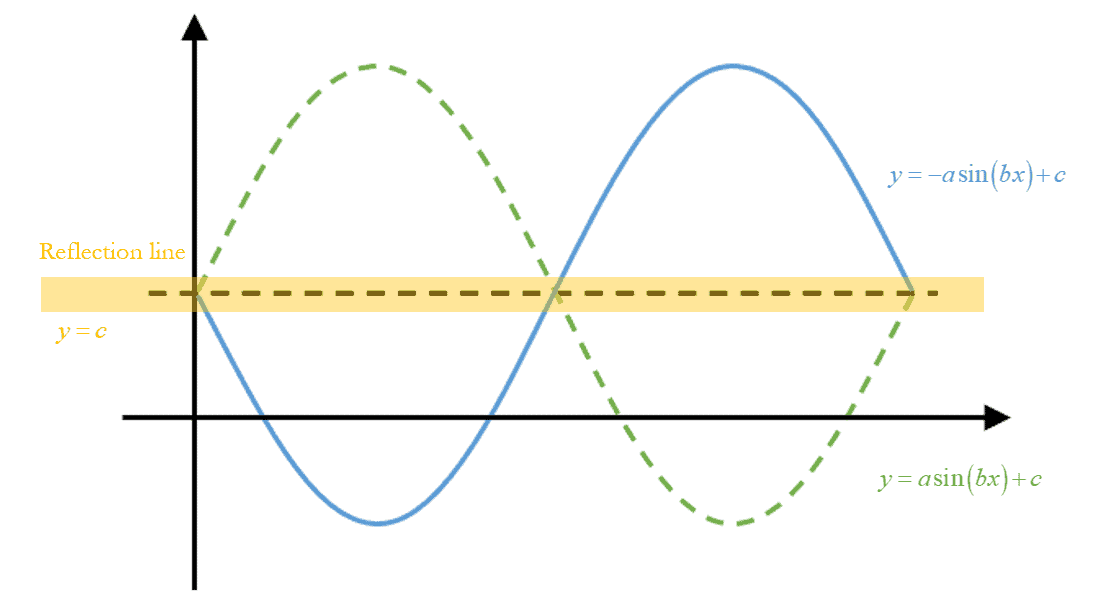
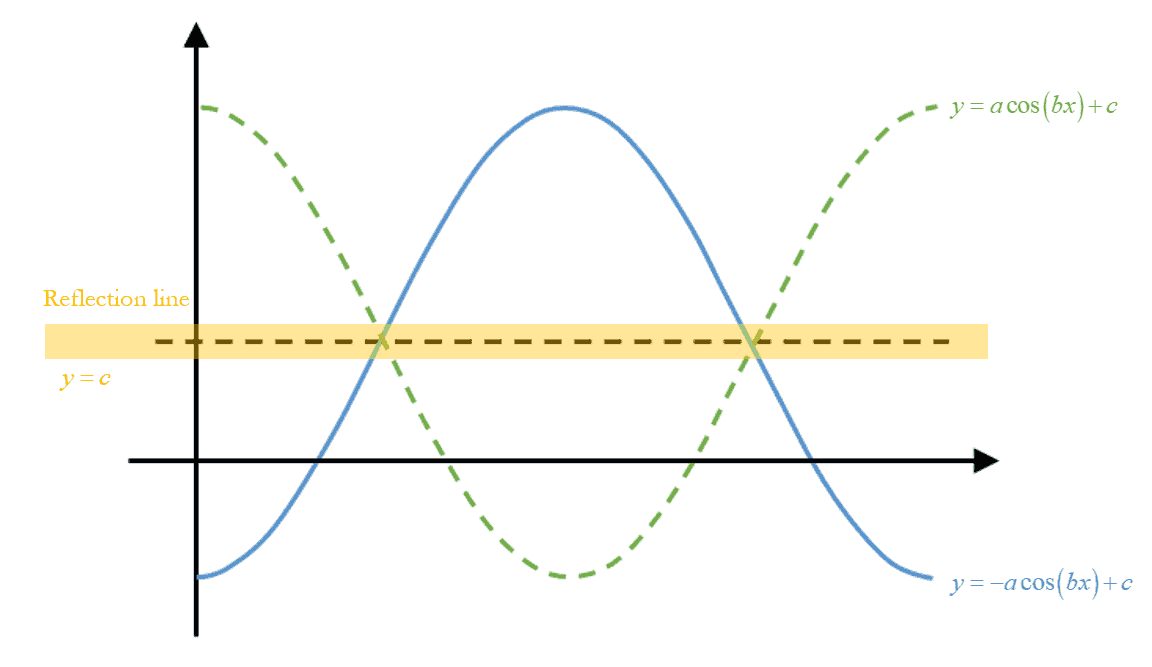
Sketch of Trigonometric Functions with $a<0$
From the previous section, we know that we can alter the shape of the sinusoidal curve by manipulating the amplitude. The amplitude of a curve is the distance from the center to either peak or trough. It can be positive or negative. Now, what if the amplitude of the graph becomes negative?
We could expect a change in the amplitude of the curve. The new graph has a negative amplitude. It does not go up from left to right; it goes down from left to right! In fact, it looks just like our original graph except that it’s reflected across the $x$-axis!
$y=a\sin(bx),a<0$
$y=a\sin(bx)+c,a<0$
$y=a\cos(bx),a<0$
$y=a\cos(bx)+c,a<0$
$y=a\tan(bx),a<0$
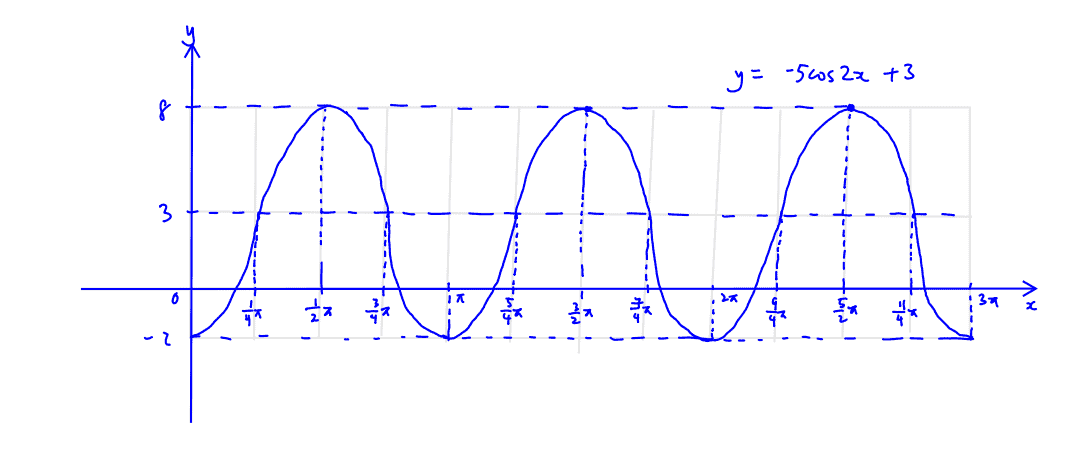
Practice Question 5
Sketch the graph of $y=-5\cos 2x+3$ for $0 \le x \le 3\pi$.
Period$=\frac{2\pi }{2}=\pi $
No. of cycles$=\frac{3\pi }{\pi }=3$
Amplitude $=\left| -5 \right|=5$
Click to enlarge image
Do sign up for our Free Mini-Courses and try our well-structured curriculum to see how it can help to maximize your learning in mathematics online.
Secondary School Additional Mathematics Free Online Course Sign Up.
You may also find the pricing and plans for our Additional Mathematics unlimited all-access courses here!
Topic List
Free Mini Course
With our online courses, you can learn at your own pace and take your time whenever it’s most convenient for you. Experience learning with us now for free!
Topics included:
- Derivative as a Gradient Function
- Chain Rule
- Problems involving Tangents and Normals
- Connected Rate of Change Involving Area