1998 TYS

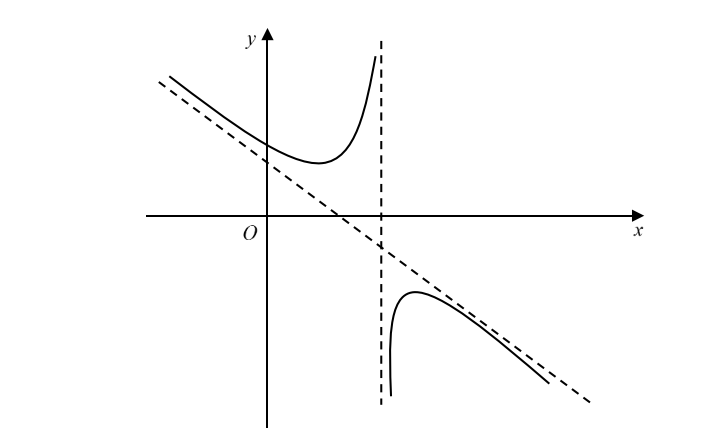
A sketch of the curve $y=\frac{a{{x}^{2}}+bx+c}{x+d}$, where $a$, $b$, $c$ and $d$ are constants, is shown, not to scale, in the diagram. The equations of the asymptotes, also shown in the diagram, are $x=2$ and $y=3-2x$.

1. Write the value of $d$.
2. State the value of $a$ and show that $b=7$.
3. Given that the curve has a stationary point where $x=1$, find the value of $c$ and the $x$-coordinate of the other stationary point.
4. Copy the above sketch and, by drawing a sketch of another suitable curve on the same diagram, show that the equation $2{{x}^{4}}-7{{x}^{3}}+8{{x}^{2}}+x-2=0$ has exactly two real roots.