2018 MJC J2 MYE Q6 (b) Modified
A point $A$ with position vector $\overrightarrow{OA}=\alpha \,\mathbf{i}+\beta \,\mathbf{j}+\gamma \,\mathbf{k},$ where $\alpha ,\,\beta $ and $\gamma $ are real constants, has direction cosines $\cos \theta ,\,\,\cos \phi $ and $\cos \delta ,$ where $\theta ,\,\phi $ and $\delta $ are the angles $\overrightarrow{OA}$ makes with the positive $x,\,y$ and $z$-axes respectively.
(i)
Express the direction cosines $\cos \theta ,\,\,\cos \phi $ and $\cos \delta $ in terms of $\alpha ,\,\beta $ and $\gamma .$ Hence find the value of ${{\cos }^{2}}\theta +{{\cos }^{2}}\phi +{{\cos }^{2}}\delta .$
(ii)
The vector $\mathbf{d}$ makes angle of $45{}^\circ $ with the $x$-axis, $60{}^\circ $ with the $y$-axis and $\delta $ with the $z$-axis, where $0{}^\circ \le \delta \le 90{}^\circ .$ Find the value of $\delta .$ If the magnitude of $\mathbf{d}$ is $12,$ express $\mathbf{d}$ in cartesian form.
Suggested Handwritten and Video Solutions
- (i)
- (ii)

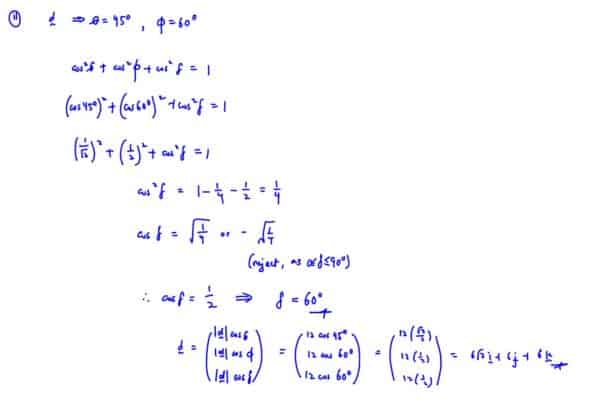
- (i)
- (ii)

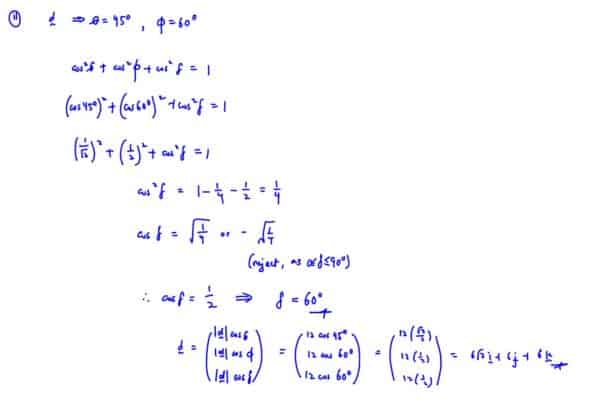
Share with your friends!
