2020 DHS Promo Q3
Functions $\text{f}$ and $\text{g}$ are defined by
$\text{f}:x\mapsto {{x}^{2}}+cx+d,x\in \mathbb{R},$ where $c$ and $d$ are constants,
$\text{g}:x\mapsto \ln x,x\in \mathbb{R},x>0$.
(i)
Given that the composite function $\text{gf}$ exists, find an inequality involving $c$ and $d$.
[2]
For the rest of the question, take $c=2,d=4$.
(ii)
Write down an expression for $\text{gf}\left( x \right)$ and find exactly the range of $\text{gf}$.
[3]
(iii)
The graph of a function $\text{h}$ is symmetrical about the line $x=k$ if $\text{h}\left( x+k \right)=\text{h}\left( -x+k \right)$ for all valid values of $x$. Using this definition, show that the graph of $\text{gf}$ is symmetrical about the line $x=-1$.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)

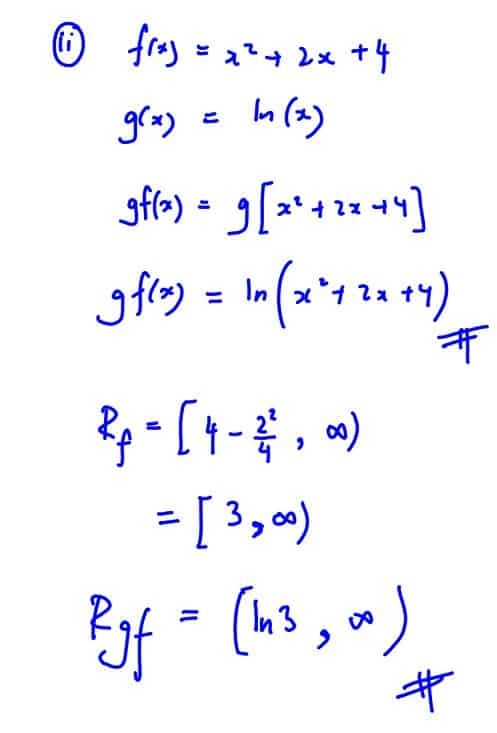
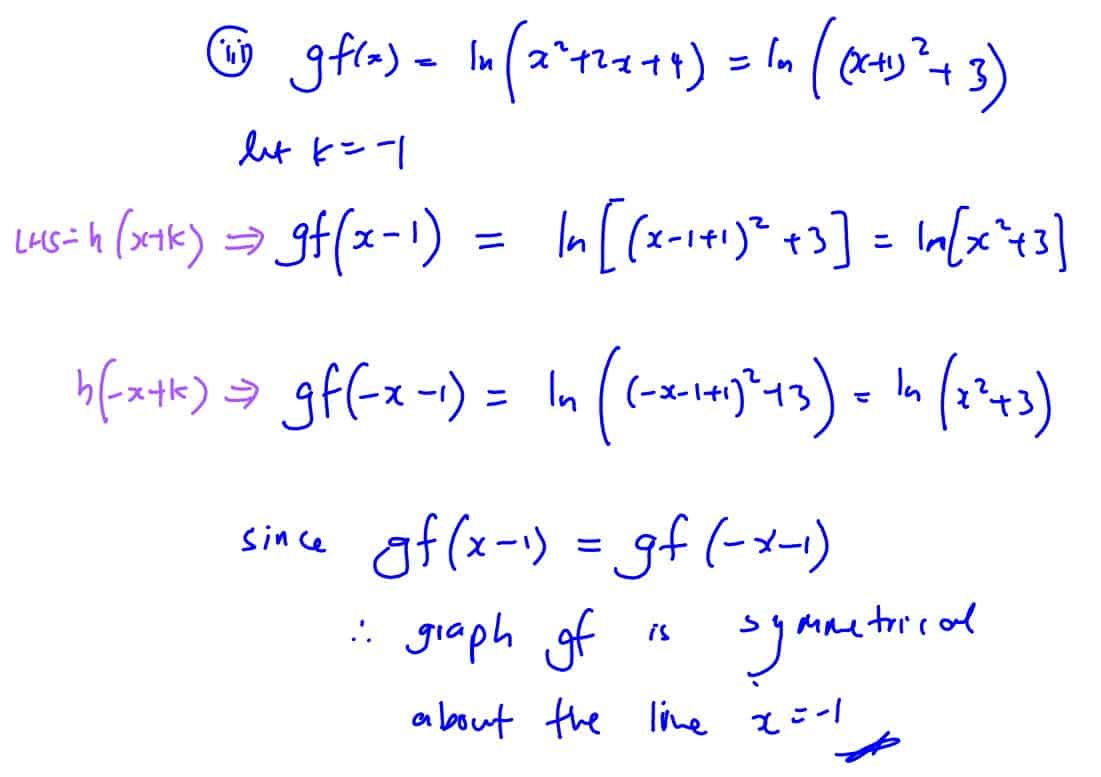
- (i)
- (ii)
- (iii)

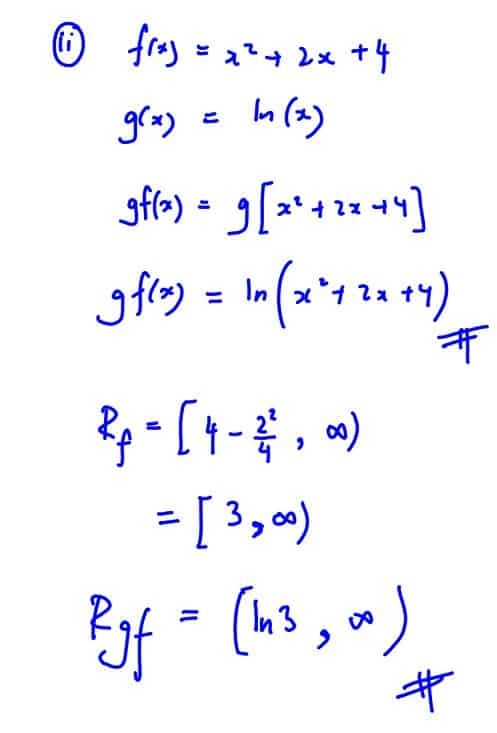
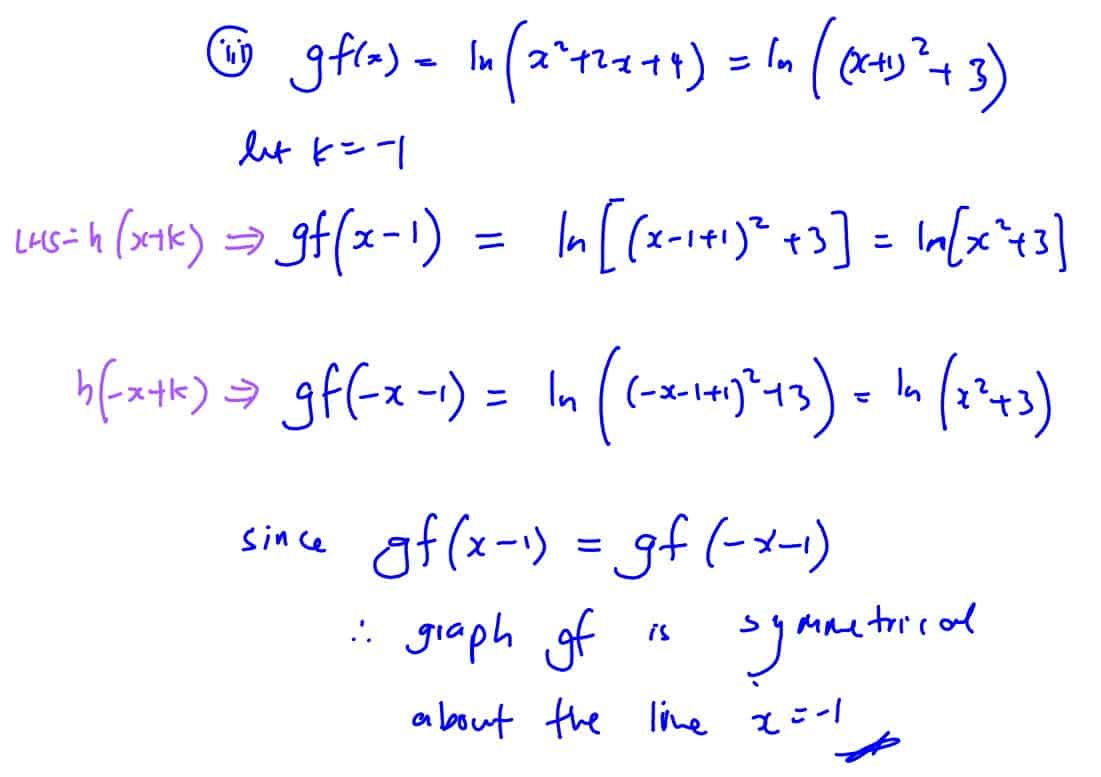
Share with your friends!
WhatsApp
Telegram
