Differentiation and Its Applications
Question 1
The diagram shows part of the curve $y=x\left( \frac{k}{\sqrt{x}}-1 \right)$, where $A$ is a point on the curve and $k$ is a positive constant. Given also that $y=\frac{25}{4}$ is a tangent to the curve at $A$,
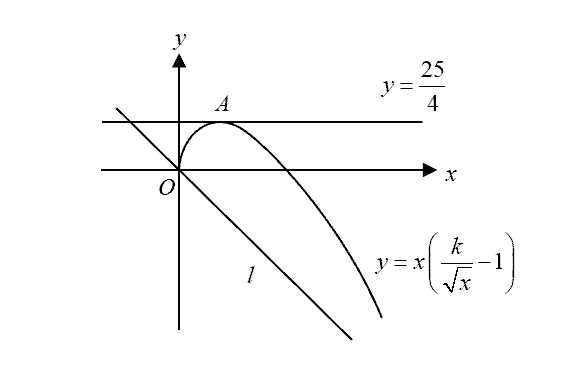
(i)
determine the value of $k$.
As $x$ gets large, the curve tends towards the line $l$.
(ii)
Explain why the gradient of $l$ is $-1$ and write down its equation.
(i) 
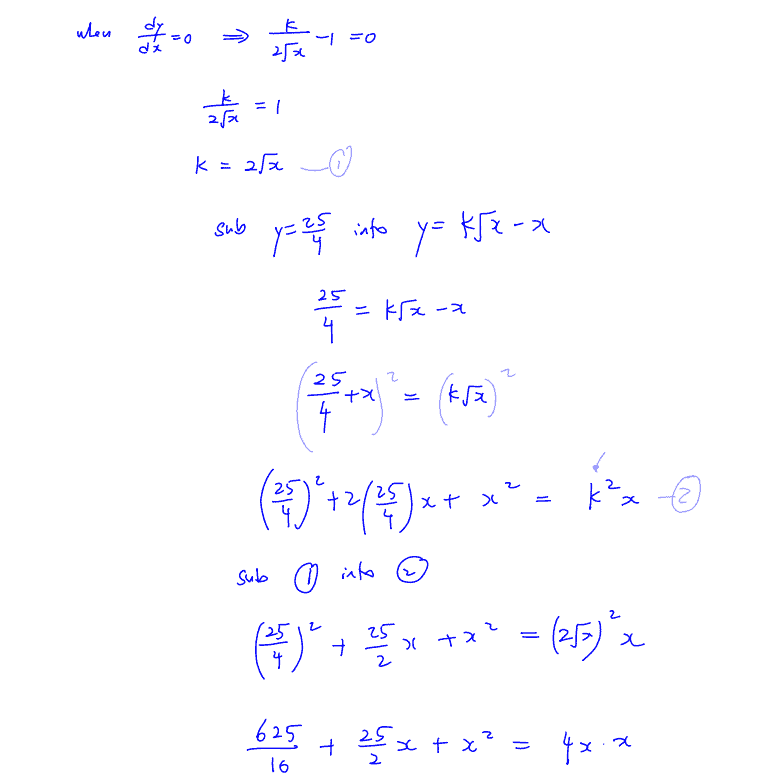
(ii) 
Question 2
Given that $y=a{{x}^{5}}$, where $a\ne 0$ , and $\frac{\text{d}y}{\text{d}x}=\frac{3}{2}$ at $\left( 1,b \right)$, find
(i)
the value of $a$ and of $b$,
(ii)
the equation of the tangent to the curve at the origin.
(i)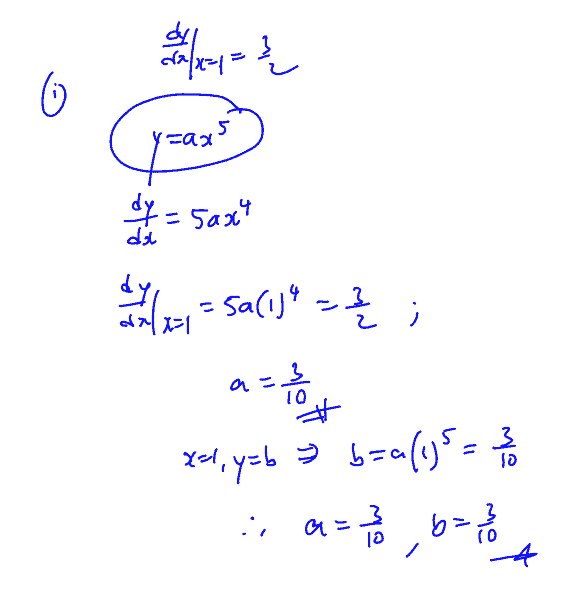 
(ii)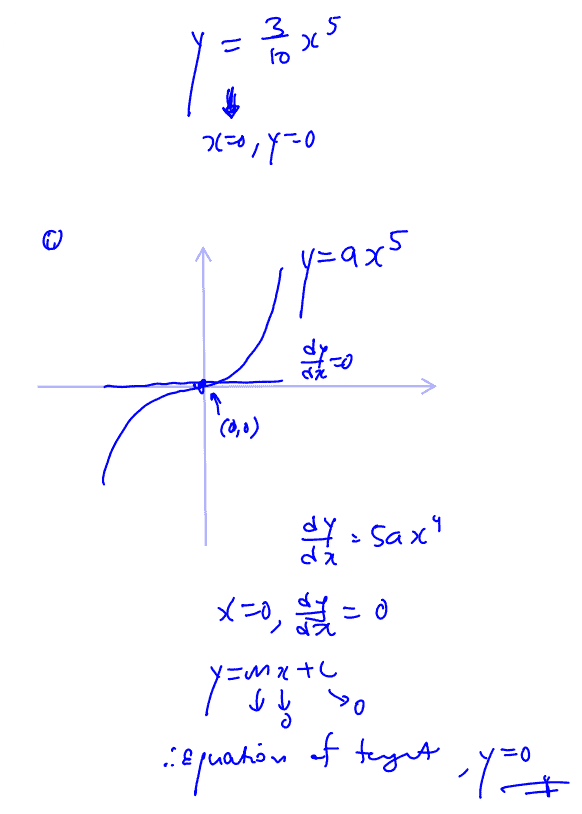 
Question 3
Finding the coefficient of a function given the gradient of a tangent at a point
The gradient of the tangent to the curve $y=a{{x}^{2}}+bx$ at the point $\left( 2,7 \right)$ is equal to $6$. Find the value of $a$ and of $b$.
Question 4
Finding the rate of change of a man’s shadow as he is walking away from lamp post
A man $1.8$ metres tall is walking at a constant rate of $1.25$ m/s away from a lamp post which is $8$ metres tall. How fast is the length of his shadow changing?
Question 5
Ladder sliding down a wall: Finding the velocity of the point of contact with the wall
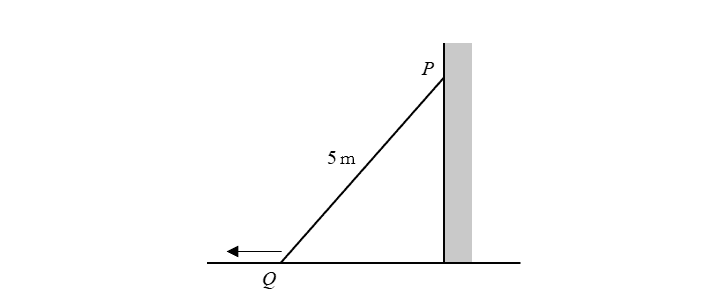
A ladder $PQ$, of length $5$m, is leaning against a wall. The lower end $Q$ of the ladder is sliding away from the wall at a constant rate of $0.6$ m/s. Find the velocity of the upper end $P$ when $Q$ is $4$m from the wall.
Question 6
If $z=\text{f}\left( x \right)\text{g}\left( y \right)$, find $\frac{\text{d}z}{\text{d}t}$ in terms of $\frac{\text{d}y}{\text{d}t}$ and $\frac{\text{d}x}{\text{d}t}$. (without implicit implication)
If $z=\text{f}\left( x \right)\text{g}\left( y \right)$, where $x$ and $y$ each vary with time $t$, what is $\frac{\text{d}z}{\text{d}t}$ ?
Question 7
Finding the equation of tangent of a quadratic curve parallel to a line
The points $P(1,2)$ and $Q(7,\text{ }14)$ lie on the curve whose equation is $y={{x}^{2}}6x+7$.
$A$ is a point on the curve such that the tangent to the curve at $A$ is parallel to $PQ$.
Find
(i)
the coordinates of $A$,
(ii)
the equation of the normal to the curve at $A$.
The normal to the curve at $A$ meets the curve again at $B$. Find
(iii)
the coordinates of $B$.
(i)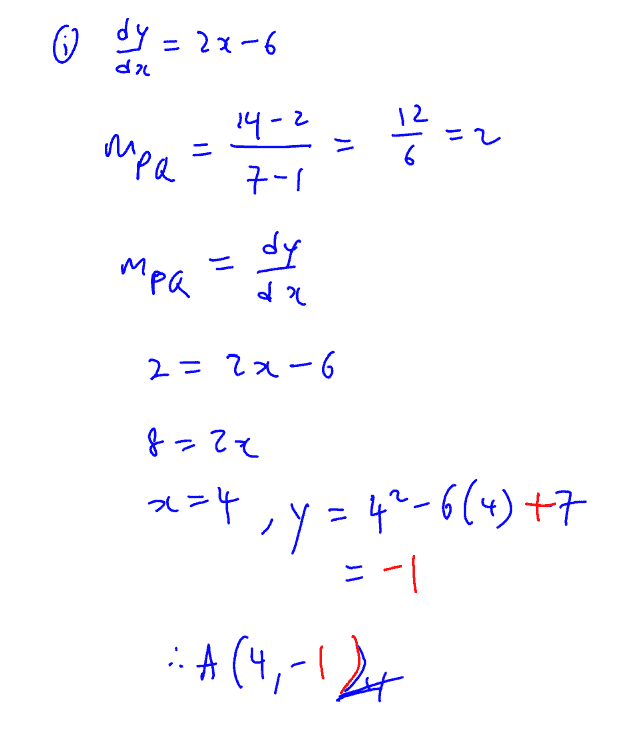 
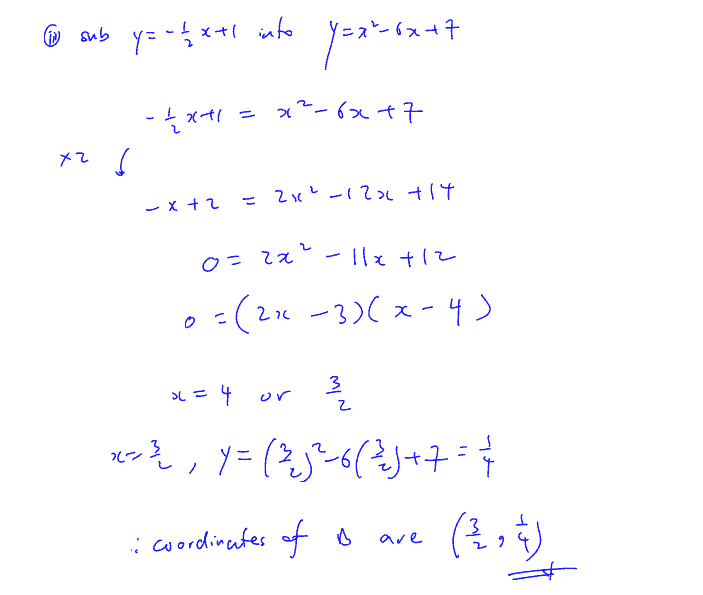
(ii)
(iii)
Question 8
Show that a function is decreasing for a given domain using partial fractions
(i)
Express $\frac{7{{x}^{3}}+{{x}^{2}}+5x+3}{\left( {{x}^{2}}+3 \right)\left( {{x}^{2}}-1 \right)}$ in partial fractions.
(ii)
Show that when $x<-\sqrt{3}$, $\frac{\text{d}}{\text{d}x}\left( \frac{7{{x}^{3}}+{{x}^{2}}+5x+3}{\left( {{x}^{2}}+3 \right)\left( {{x}^{2}}-1 \right)} \right)<0$.
(ii)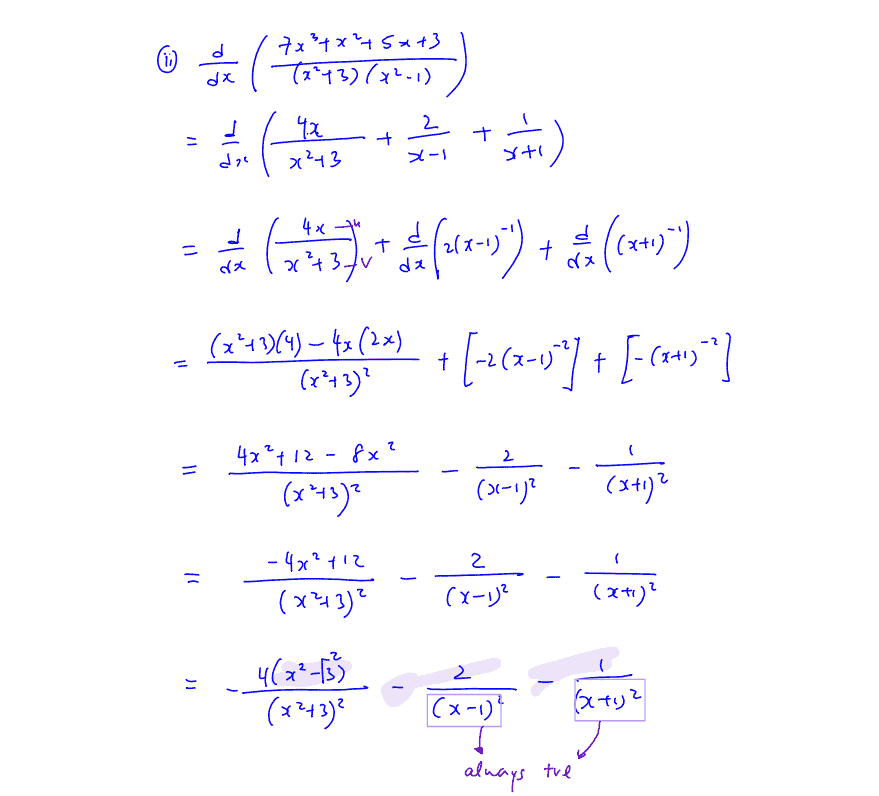 
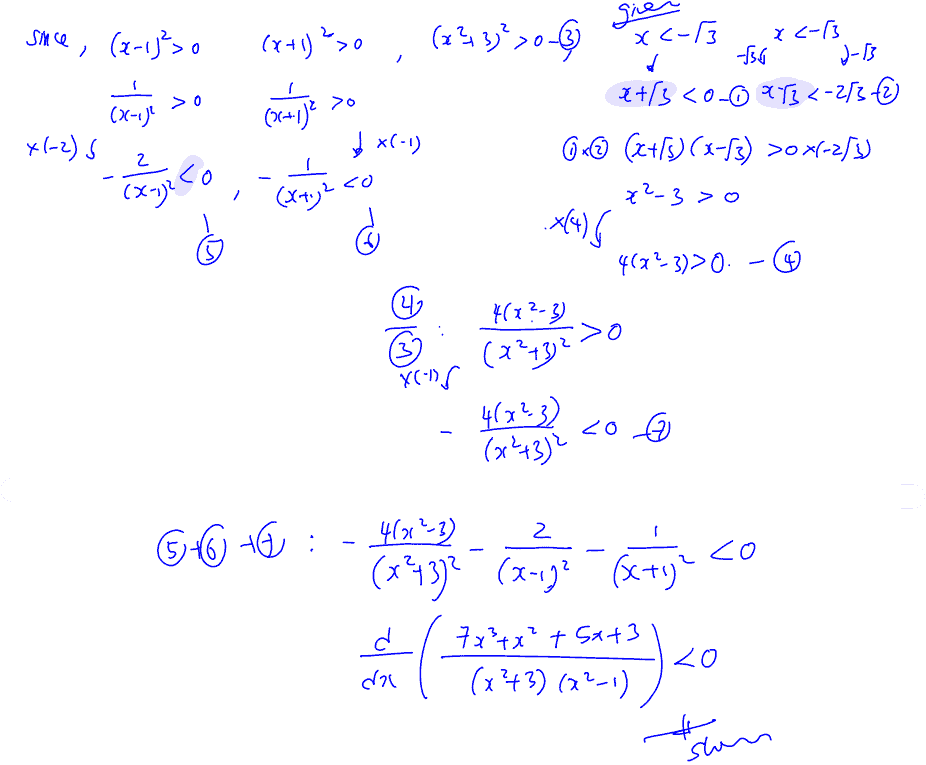
Question 9
The gradient of the curve $y=\frac{2}{3}{{\left( ax-1 \right)}^{n}}$ at the point $\left( \frac{1}{3},\frac{2}{3} \right)$ is $20$. Find the values of constants $a$ and $n$.
Question 10
There are two points on the curve $y=\sqrt[3]{4{{x}^{3}}+9{{x}^{2}}-12x}$ at which the tangents are perpendicular to the line $x=7$.
Calculate the $x$- coordinates of these points.
Question 11
Finding The Minimum Volume Of A Cone With A Fixed Sphere Inscribed In It
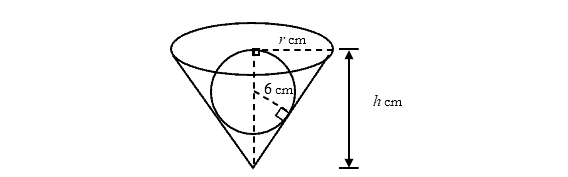
The diagram shows a solid spherical ball of radius $6$cm that rests inside a cone of height $h$cm and radius $r$cm.
(i)
Show that the volume, $V$cm$^{3}$, of the cone is given by $V=\frac{12\pi {{h}^{2}}}{h-12}$.
(ii)
Given that $h$ can vary, find the value of $h$ for which $V$ has a stationary value.
(iii)
Find this stationary value of $V$ and determine whether this value of $V$ is a maximum or minimum.
(i) 
(ii) 
(iii) 
Question 12
Water is poured into a hemispherical bowl of radius $6$ cm at a rate of $20$ cm$^{3}$/s. After $t$ seconds, the volume of water in the bowl, $V$ cm$^{3}$, is given by $V=6\pi {{x}^{2}}-\frac{1}{3}\pi {{x}^{3}}$, where $x$ cm is the height of water in the bowl.
(a)
Calculate the rate of change of $x$ when $x=4$ cm, giving your answer in terms of $\pi$.
(b)
Will the rate of change of $x$ increase when $x=5$? Explain your answer clearly.
(a)
(b)
Question 13
A vessel is in the shape of a right circular cone. The radius of the top is $8$ cm and the height is $40$ cm.
Water is poured into vessel at a rate of $20$ cm$^{3}$/s. Calculate the rate at which water level is rising when
(a)
the water level is $12$ cm from the vertex,
(Leve your answer in terms of $\pi$)
(b)
the vessel is one-quarter full.
(Leave you answer correct to $3$ significant figures)
(a)
(b)
