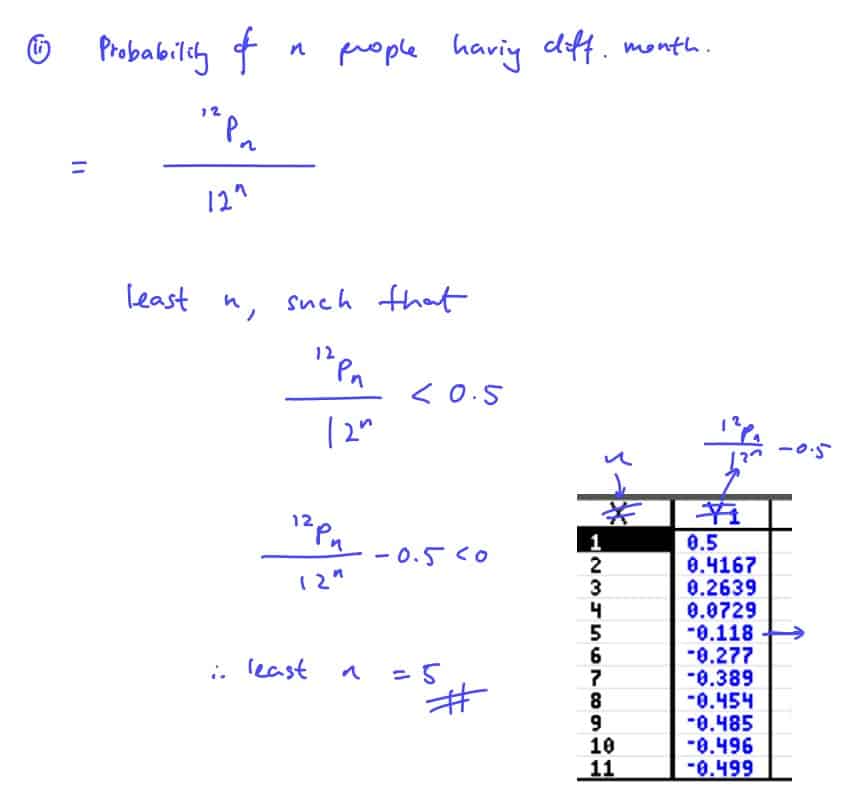
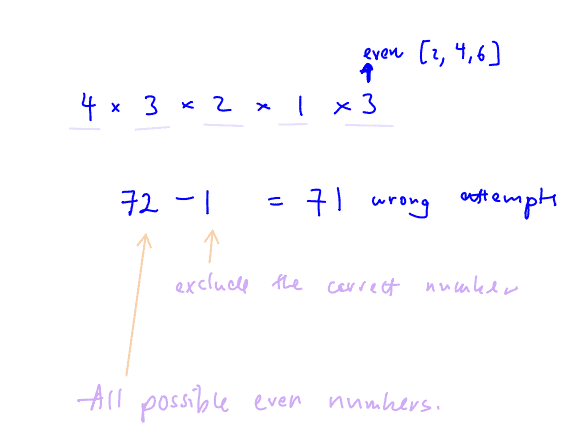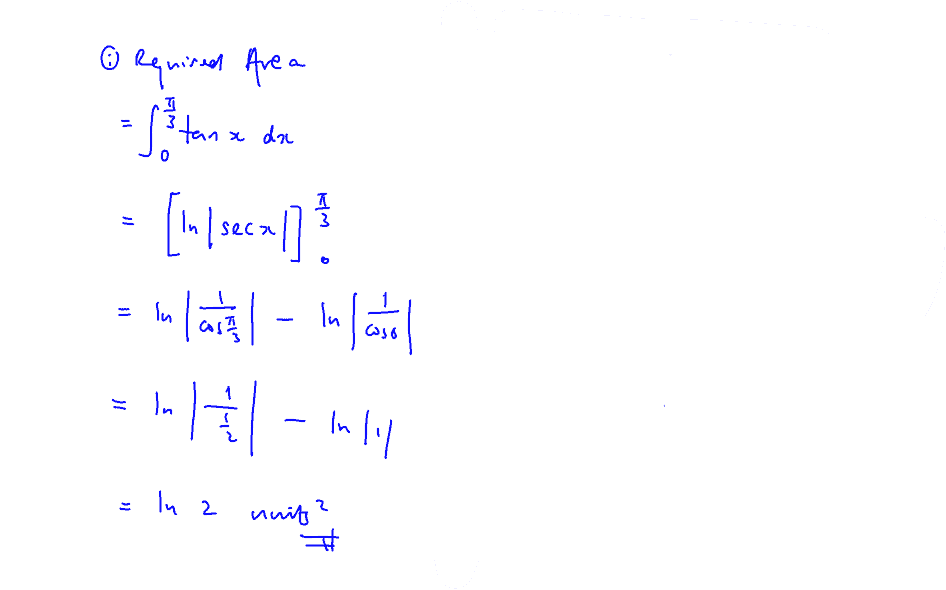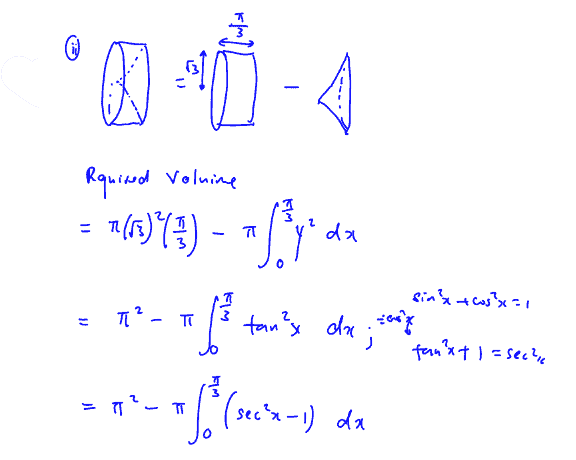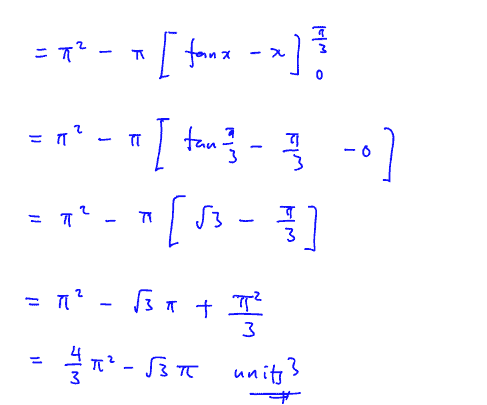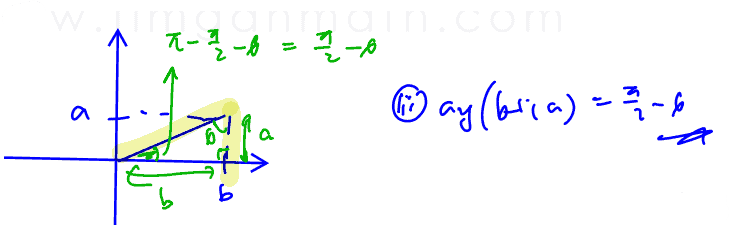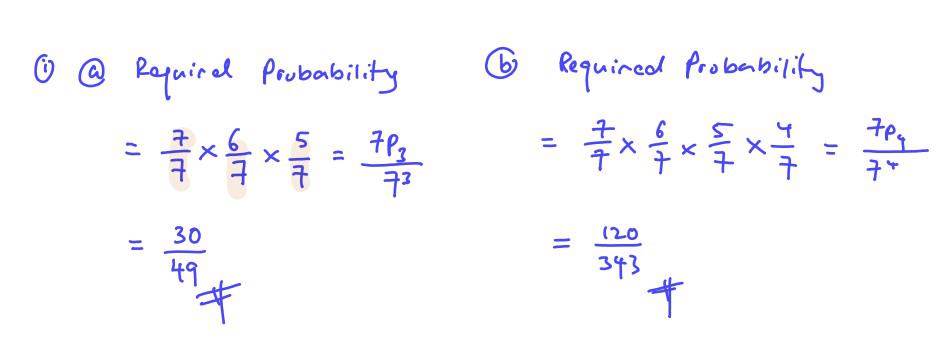Ten-Year-Series (TYS) Solutions | Past Year Exam Questions

2002 A Level H2 Math

These Ten-Year-Series (TYS) worked solutions with video explanations for 2002 A Level H2 Mathematics are suggested by Mr Gan. For any comments or suggestions please contact us at support@timganmath.edu.sg.

Select Year

2021

Paper 1

Paper 2

Ten-Year-Series (TYS) Solutions | Past Year Exam Questions

2002 A Level H2 Math

2021

2011-2020

2001-2010

1991-2000

1981-1990

1971-1980

2002 A Level H2 Math Paper 1 Question 3

Suggested Handwritten and Video Solutions

2002 A Level H2 Math Paper 1 Question 7

Suggested Handwritten and Video Solutions

2002 A Level H2 Math Paper 1 Question 14

Suggested Handwritten and Video Solutions

2002 A Level H2 Math Paper 2 Question 2 (b)

Suggested Handwritten and Video Solutions

2002 A Level H2 Math Paper 2 Question 30

Suggested Handwritten and Video Solutions