
5 Exam Preparation Tips: How We Help Students Excel in Exams
In the ever-evolving landscape of education, where academic success is often measured by performance in exams, the need for effective test preparation has never been
These Ten-Year-Series (TYS) worked solutions with video explanations for 2019 A Level H2 Mathematics are suggested by Mr Gan. For any comments or suggestions please contact us at support@timganmath.edu.sg.
A function is defined as $\text{f}\left( x \right)=2{{x}^{3}}-6{{x}^{2}}+6x-12$.
(i)
Show that $\text{f}\left( x \right)$ can be written in the form $p\left\{ {{\left( x+q \right)}^{3}}+r \right\}$, where $p,q$ and $r$ are constants to be found.
[2]
(i) Show that $\text{f}\left( x \right)$ can be written in the form $p\left\{ {{\left( x+q \right)}^{3}}+r \right\}$, where $p,q$ and $r$ are constants to be found.
[2]
(ii)
Hence, or otherwise, describe a sequence of transformations that transform the graph of $y={{x}^{3}}$ onto the graph of $y=\text{f}\left( x \right)$.
[3]
(ii) Hence, or otherwise, describe a sequence of transformations that transform the graph of $y={{x}^{3}}$ onto the graph of $y=\text{f}\left( x \right)$.
[3]
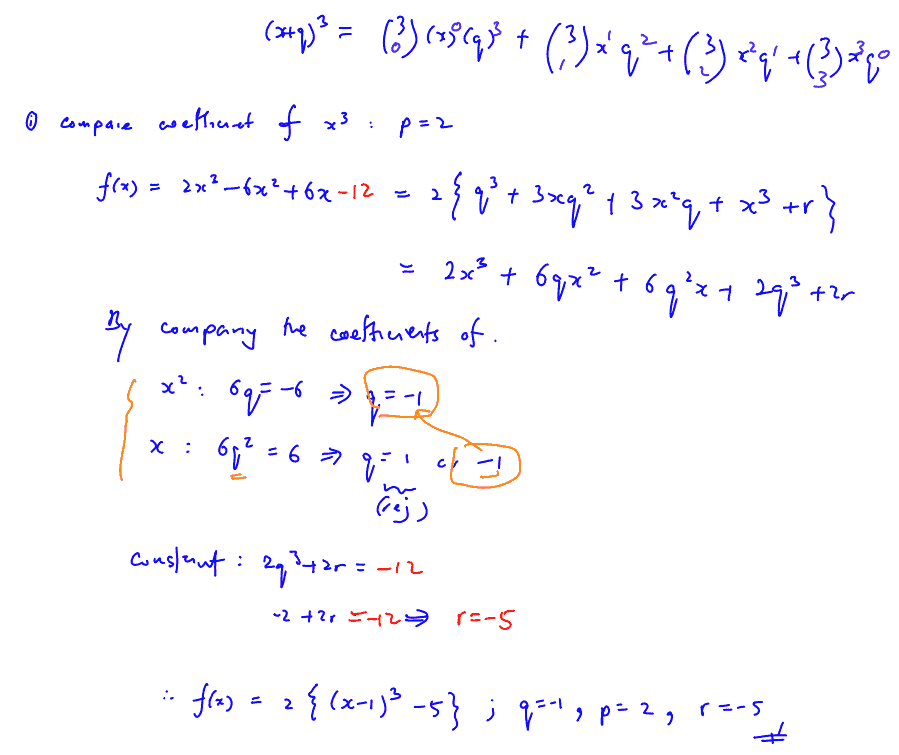

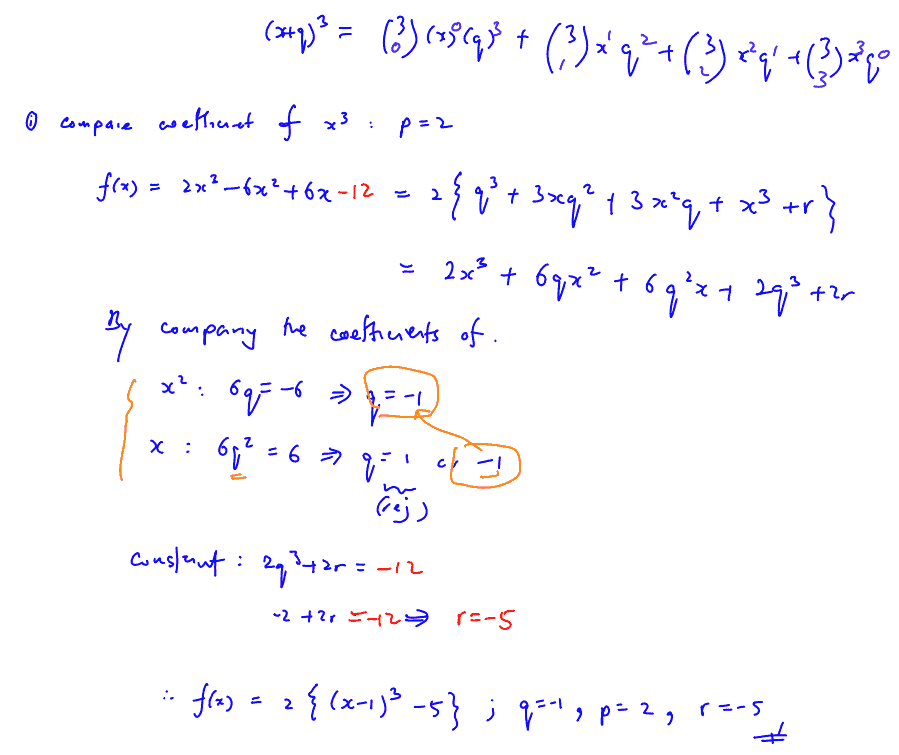

Share with your friends!
(i)
Sketch the graph of $y=\left| {{2}^{x}}-10 \right|$, giving the exact values of any points where the curve meets the axes.
[3]
(i) Sketch the graph of $y=\left| {{2}^{x}}-10 \right|$, giving the exact values of any points where the curve meets the axes.
[3]
(ii)
Without using a calculator, and showing all your working, find the exact interval, or intervals, for which $\left| {{2}^{x}}-10 \right|\le 6$. Give your answer in its simplest form.
[3]
(ii) Without using a calculator, and showing all your working, find the exact interval, or intervals, for which $\left| {{2}^{x}}-10 \right|\le 6$. Give your answer in its simplest form.
[3]
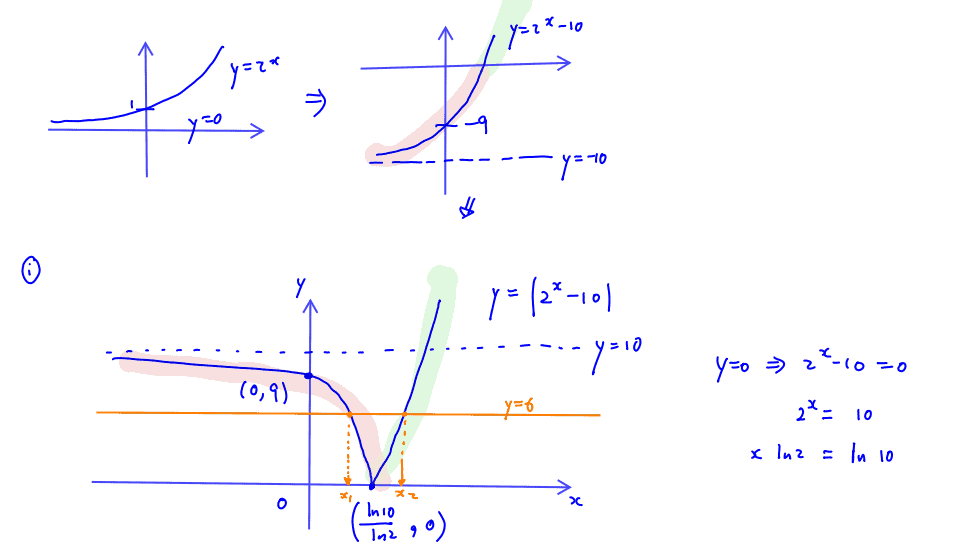

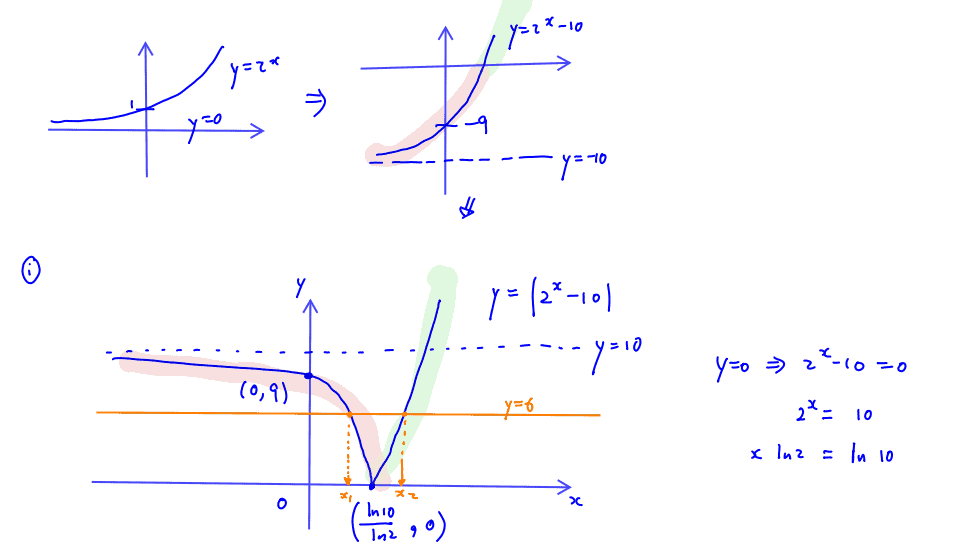

Share with your friends!
(a)
An arithmetic series has first term $a$ and common difference $2a,$where $a\ne 0.$ A geometric series has first term $a$ and common ratio $2.$ The ${{k}^{\text{th}}}$ term of the geometric series is equal to the sum of the first $64$ terms of the arithmetic series. Find the value of $k.$
[3]
(a) An arithmetic series has first term $a$ and common difference $2a,$where $a\ne 0.$ A geometric series has first term $a$ and common ratio $2.$ The ${{k}^{\text{th}}}$ term of the geometric series is equal to the sum of the first $64$ terms of the arithmetic series. Find the value of $k.$
[3]
(b)
A geometric series has first term $f$ and common ratio $r,$ where $f$, $r\in \mathbb{R}$ and $f\ne 0$. The sum of the first four terms of the series is $0.$ Find the possible values of $f$ and $r.$ Find also, in terms of $f,$ the possible values of the sum of the first $n$ terms of the series.
[4]
(b) A geometric series has first term $f$ and common ratio $r,$ where $f$, $r\in \mathbb{R}$ and $f\ne 0$. The sum of the first four terms of the series is $0.$ Find the possible values of $f$ and $r.$ Find also, in terms of $f,$ the possible values of the sum of the first $n$ terms of the series.
[4]
(c)
The first term of an arithmetic series is negative. The sum of the first four terms of the series is $14$ and the product of the first four terms of the series is $0.$ Find the ${{11}^{\text{th}}}$ term of the series.
[4]
(c) The first term of an arithmetic series is negative. The sum of the first four terms of the series is $14$ and the product of the first four terms of the series is $0.$ Find the ${{11}^{\text{th}}}$ term of the series.
[4]
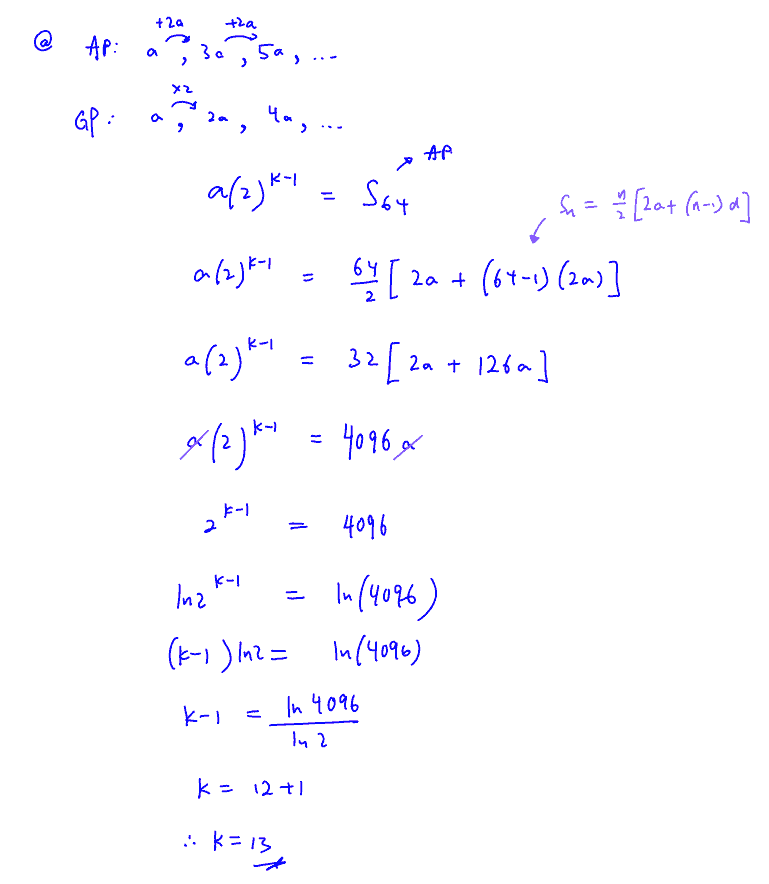
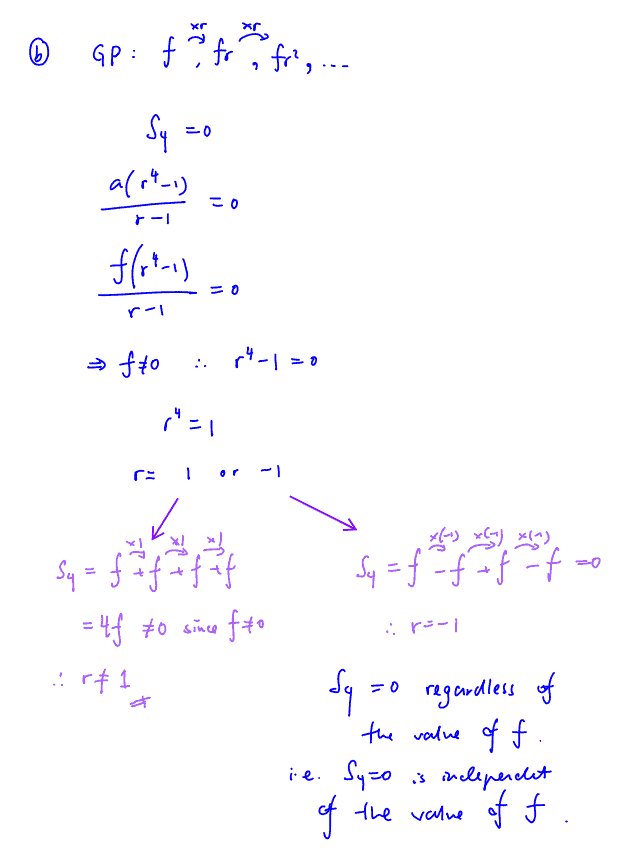
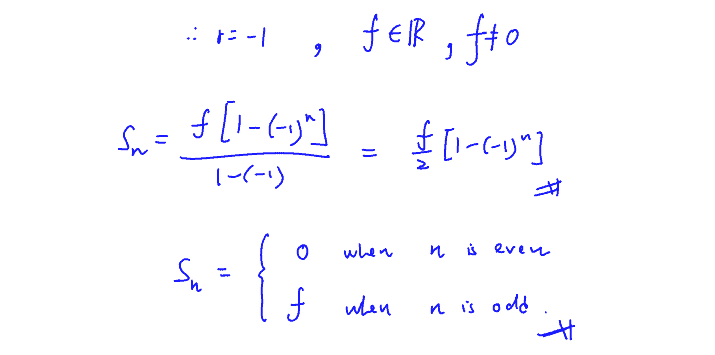
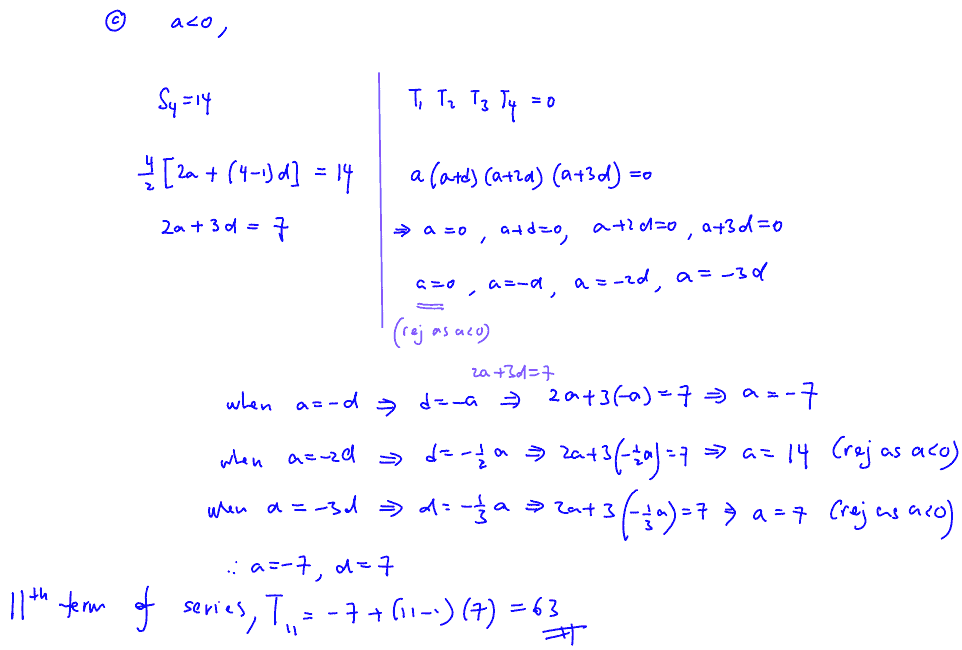
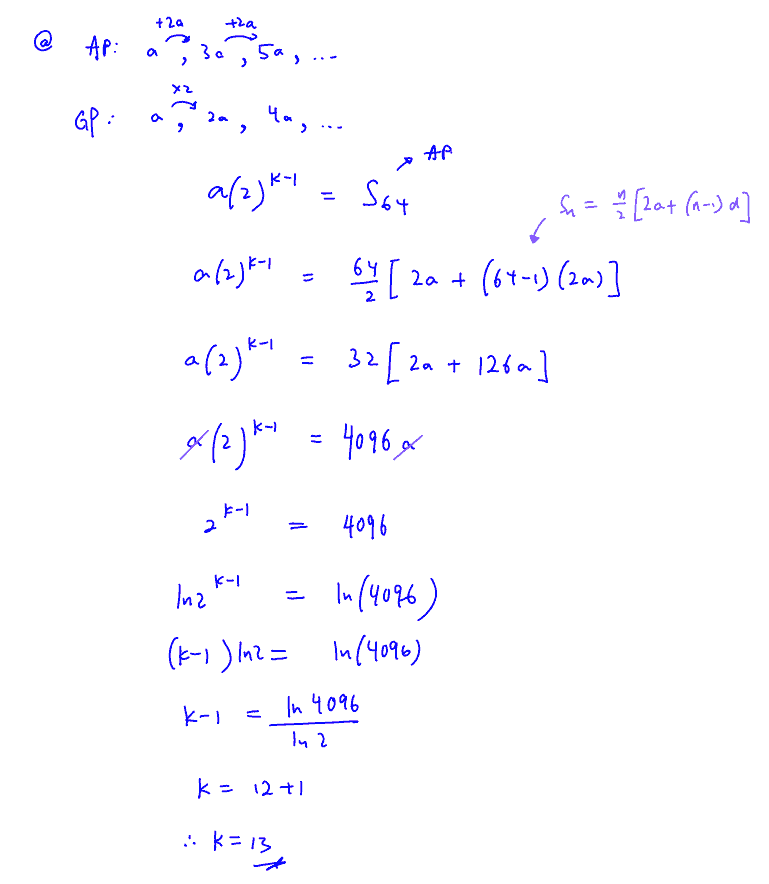
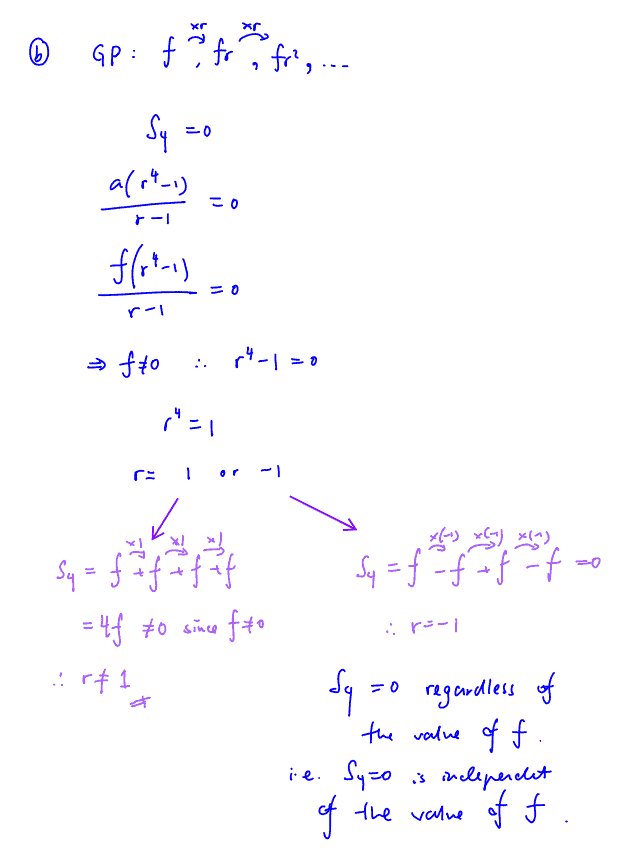
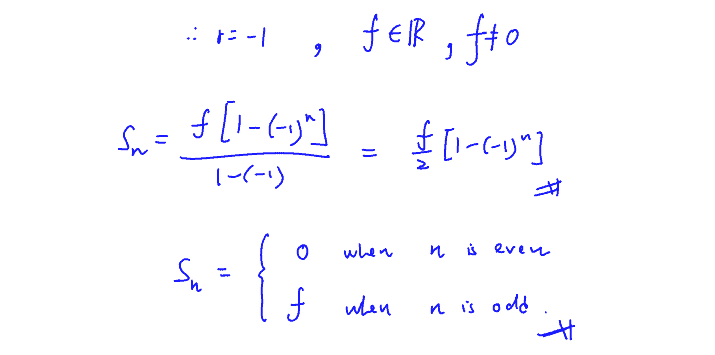
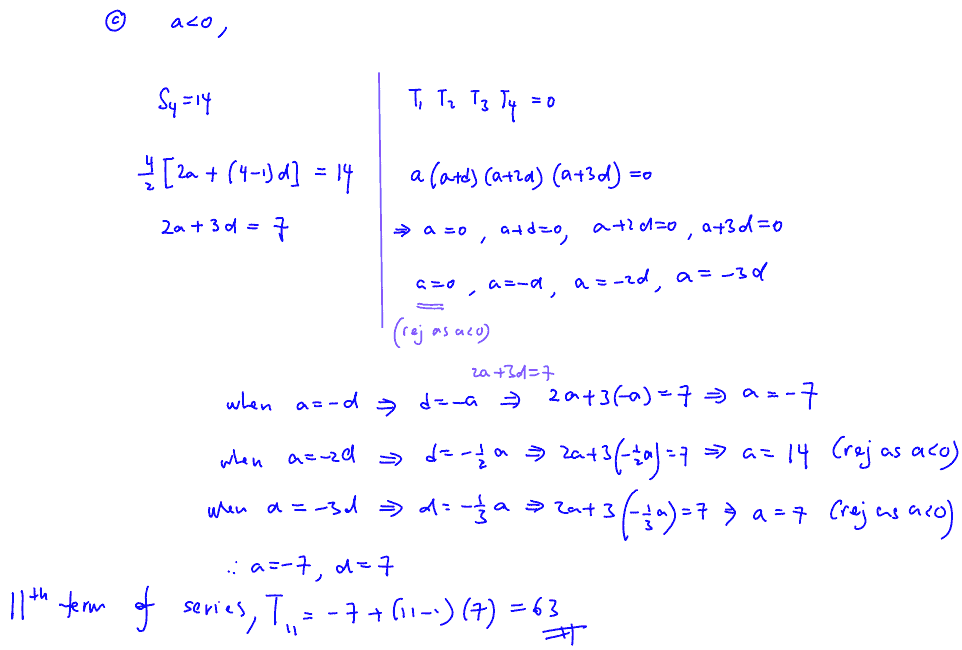
Share with your friends!
(i)
The complex number $w$ can be expressed as $\cos \,\theta +\text{i sin}\,\theta .$
(i) The complex number $w$ can be expressed as $\cos \,\theta +\text{i sin}\,\theta .$
(a) Show that $w+\frac{1}{w}$ is a real number.
[2]
(b) Show that $\frac{w-1}{w+1}$ can be expressed as $k\tan \frac{1}{2}\theta ,$ where $k$ is a complex number to be found.
[4]
(ii)
[5]
[5]








Share with your friends!
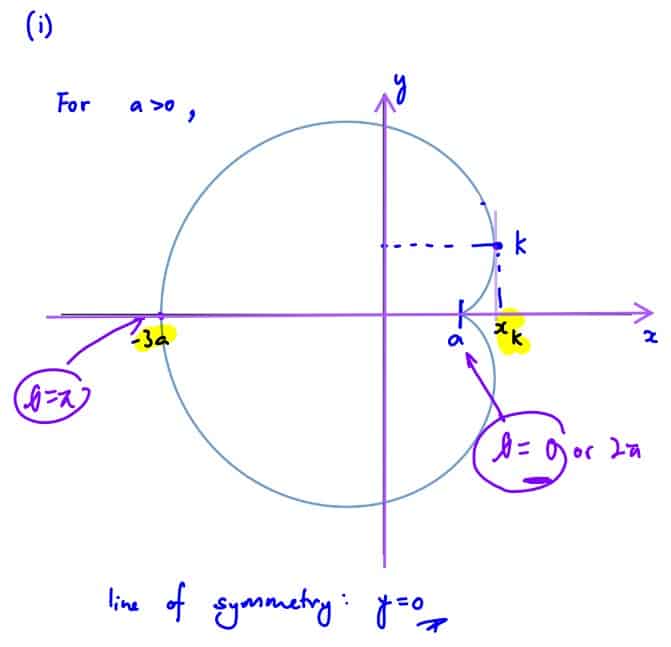
A curve $C$ has parametric equations
$x=a( 2\cos \theta -\cos 2\theta)$,
$y=a( 2\sin \theta -\sin 2\theta)$,
for $0\le \theta \le 2\pi .$
(i)
[2]
[2]
(ii)
[2]
[2]
(iii)
Show that the area enclosed by the $x$-axis, and the part of $C$ above the $x$-axis, is given by
$\int_{{{\theta }_{1}}}^{{{\theta }_{2}}}{{{a}^{2}}\left( 4{{\sin }^{2}}\theta -6\sin \theta \sin 2\theta +2{{\sin }^{2}}2\theta \right)}\,\text{d}\theta ,$
where ${{\theta }_{1}}$ and ${{\theta }_{2}}$ should be stated.
[3]
(iii) Show that the area enclosed by the $x$-axis, and the part of $C$ above the $x$-axis, is given by
$\int_{{{\theta }_{1}}}^{{{\theta }_{2}}}{{{a}^{2}}\left( 4{{\sin }^{2}}\theta -6\sin \theta \sin 2\theta +2{{\sin }^{2}}2\theta \right)}\,\text{d}\theta ,$
where ${{\theta }_{1}}$ and ${{\theta }_{2}}$ should be stated.
[3]
(iv)
[5]
[5]



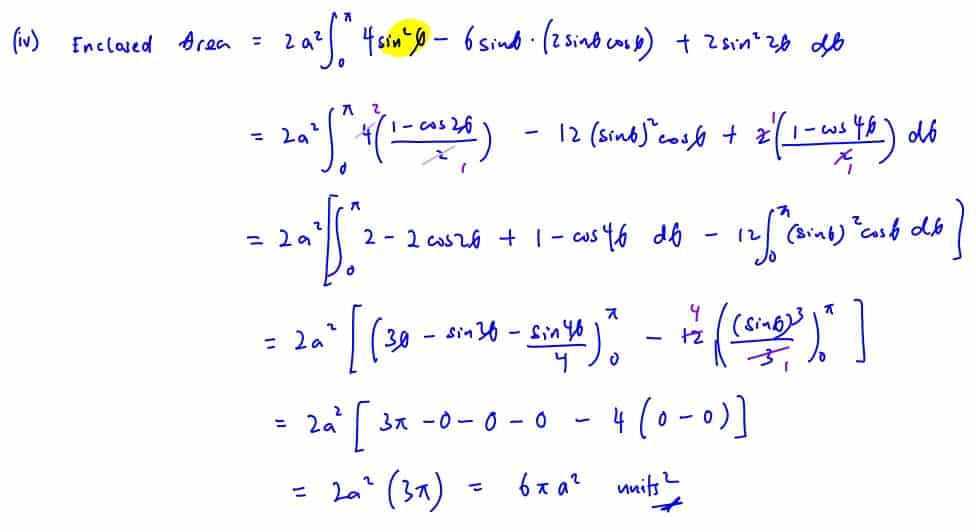




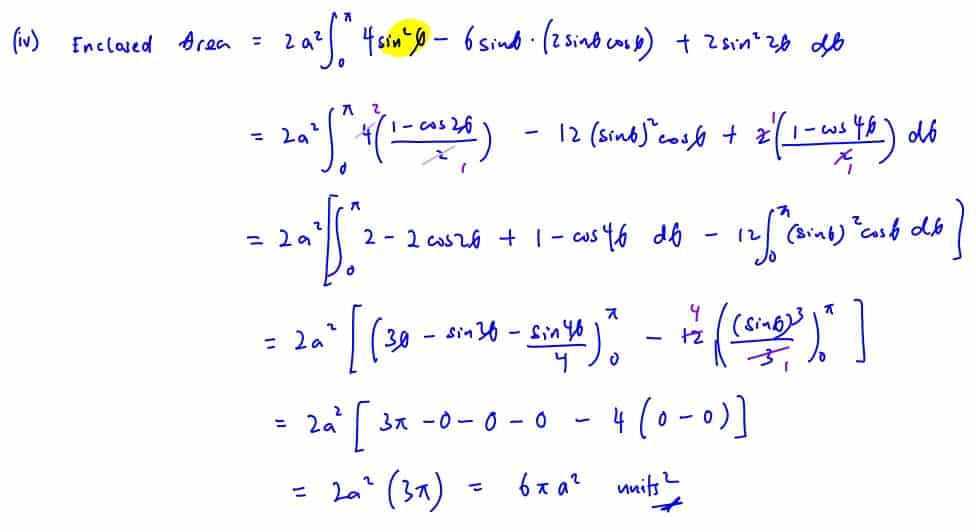
Share with your friends!
Scientists are investigating how the temperature of water changes in various environments.
(i)
The scientists begin by investigating how hot water cools.
The water is heated in a container and then placed in a room which is kept at a constant temperature of $16\,{}^\circ \text{C}$. The temperature of the water $t$ minutes after it is placed in the room is $\theta \,{}^\circ \text{C}\text{.}$ This temperature decreases at a rate proportional to the difference between the temperature of the water and the temperature of the room. The temperature of the water falls from a value of $80\,{}^\circ \text{C}$ to $32\,{}^\circ \text{C}$ in the first $30$ minutes.
(i) The scientists begin by investigating how hot water cools.
The water is heated in a container and then placed in a room which is kept at a constant temperature of $16\,{}^\circ \text{C}$. The temperature of the water $t$ minutes after it is placed in the room is $\theta \,{}^\circ \text{C}\text{.}$ This temperature decreases at a rate proportional to the difference between the temperature of the water and the temperature of the room. The temperature of the water falls from a value of $80\,{}^\circ \text{C}$ to $32\,{}^\circ \text{C}$ in the first $30$ minutes.
(a) Write down the differential equation for this situation. Solve this differential equation to get $\theta $ as an exact function of $t$.
[6]
(b) Find the temperature of the water $45$ minutes after it is placed in the room.
[1]
(ii)
The scientists then model the thickness of ice on a pond.
In winter the surface of the water in the pond freezes. Once the thickness of the ice reaches $3$ cm, it is safe to skate on the ice. The freezing of the water is modelled by a differential equation in which the rate of change of the thickness of ice is inversely proportional to its thickness. It is given that $T=0$ when $t=0.$ After $60$ minutes, the ice is $1$ cm thick.
Find the time from when freezing commences until the ice is first safe to skate on.
[6]
(ii) The scientists then model the thickness of ice on a pond.
In winter the surface of the water in the pond freezes. Once the thickness of the ice reaches $3$ cm, it is safe to skate on the ice. The freezing of the water is modelled by a differential equation in which the rate of change of the thickness of ice is inversely proportional to its thickness. It is given that $T=0$ when $t=0.$ After $60$ minutes, the ice is $1$ cm thick.
Find the time from when freezing commences until the ice is first safe to skate on.
[6]

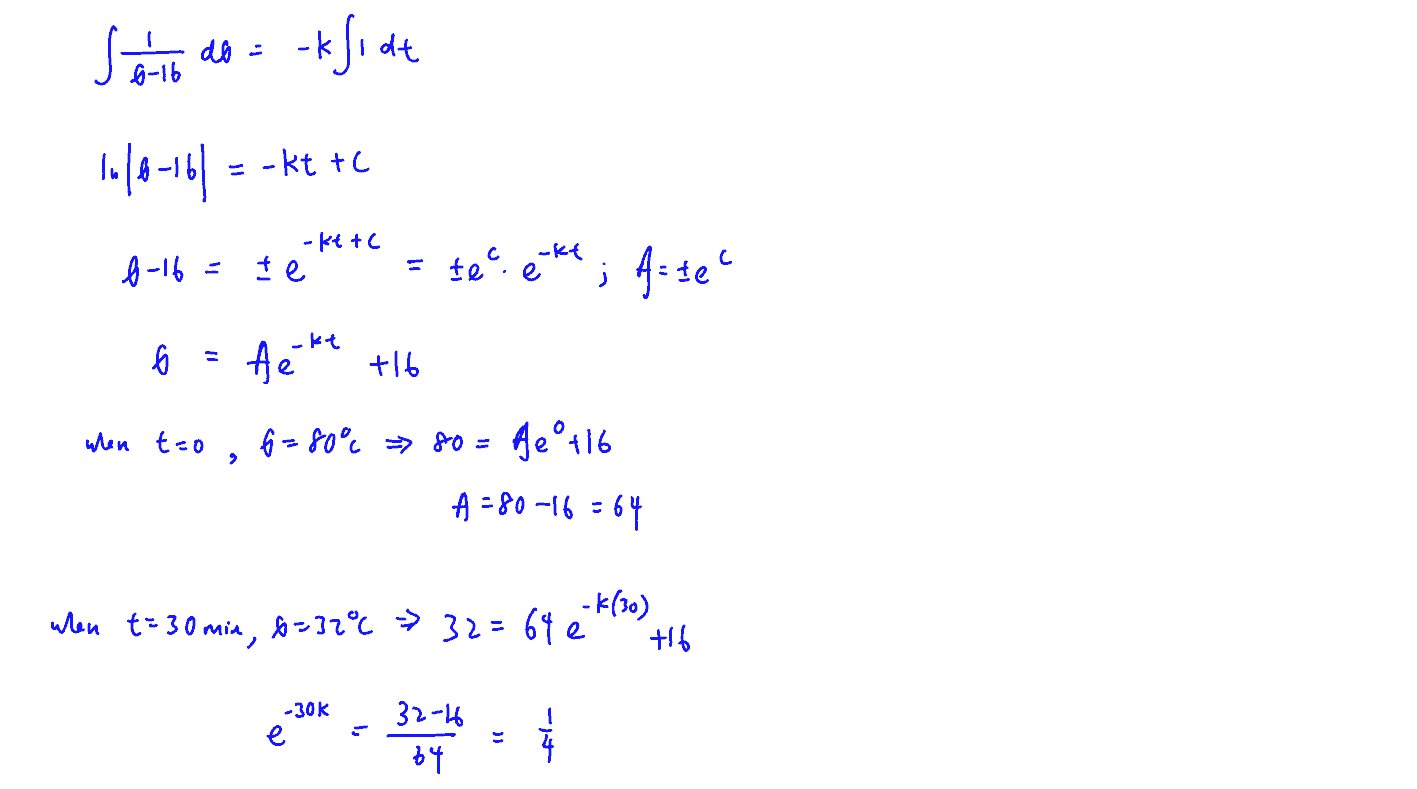
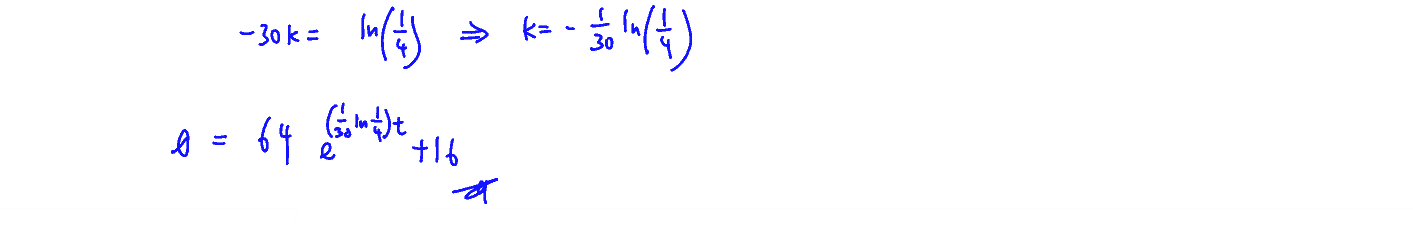
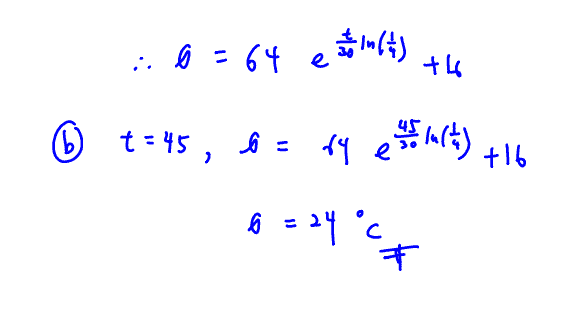

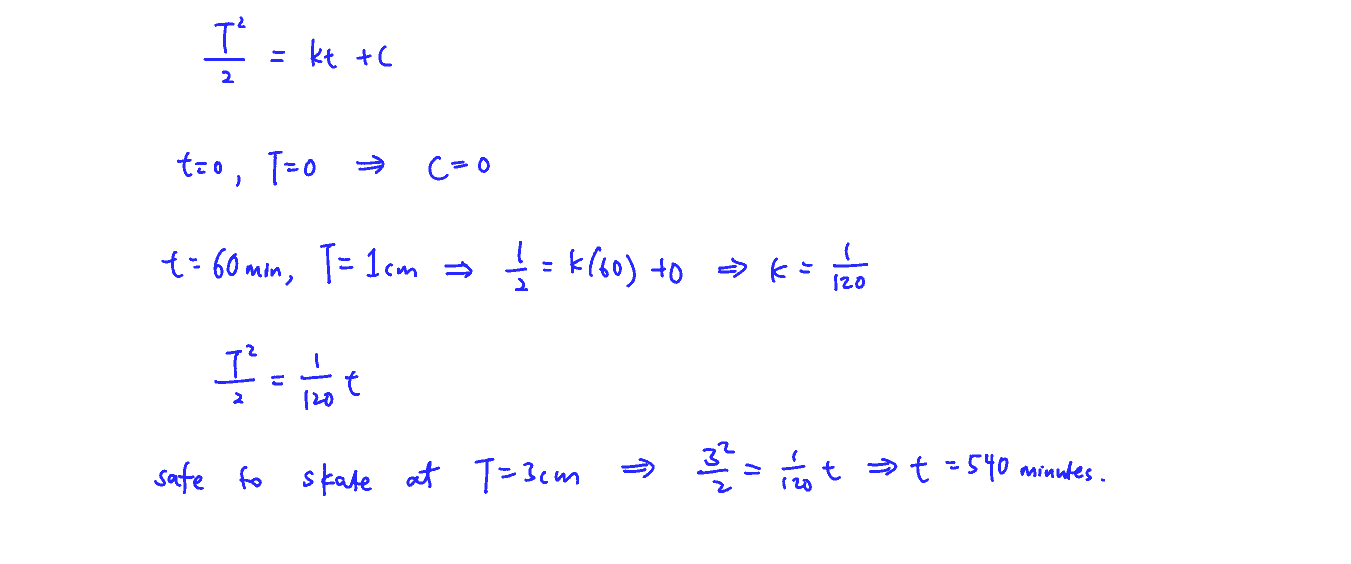

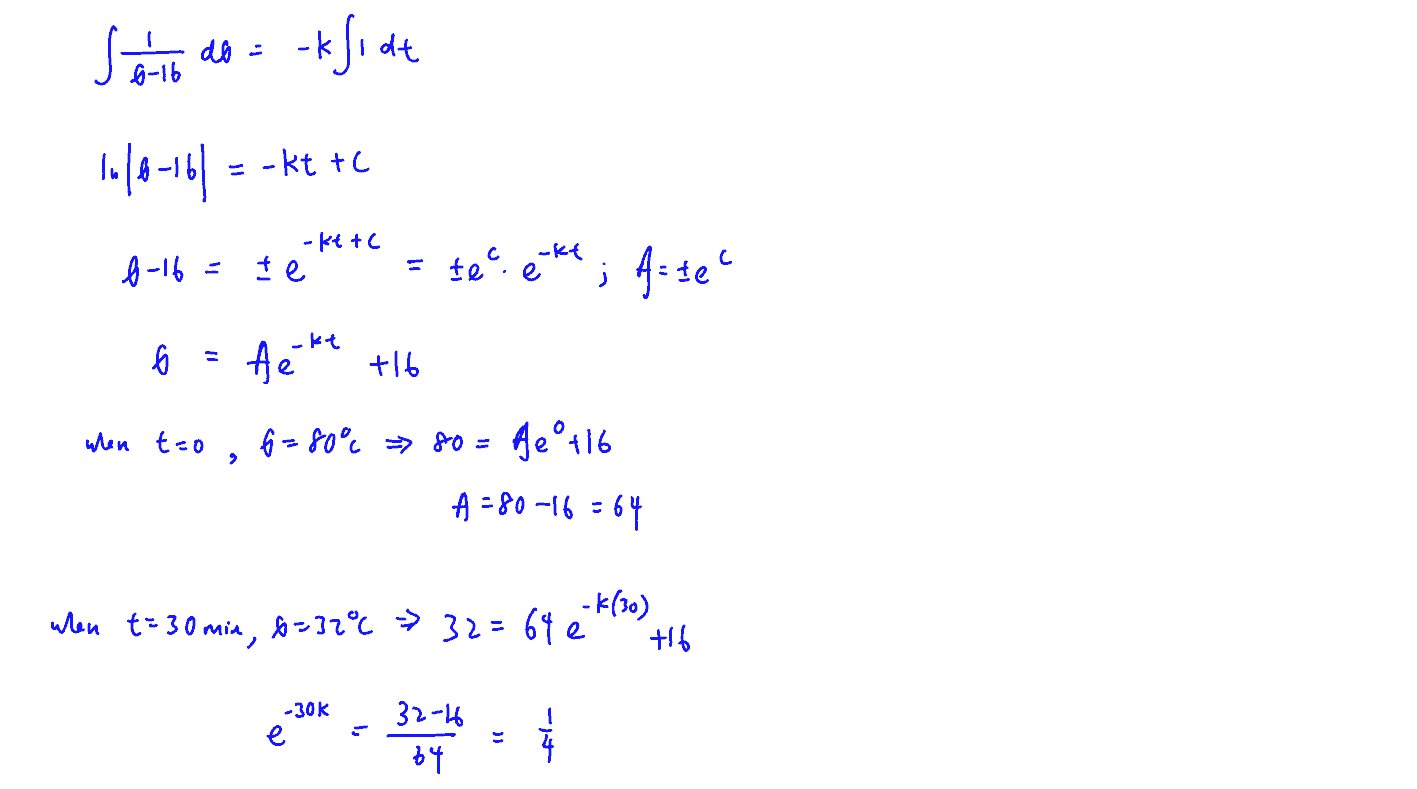
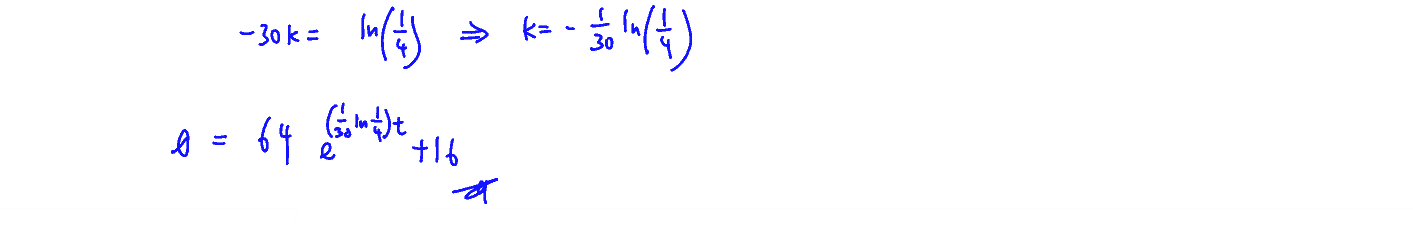
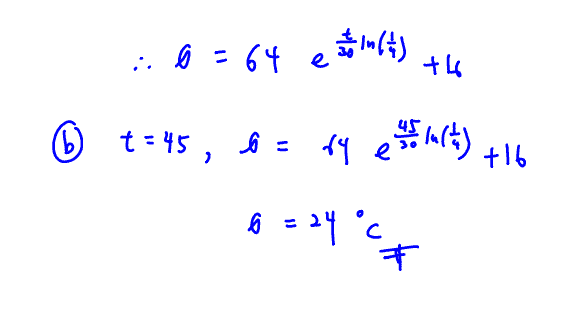

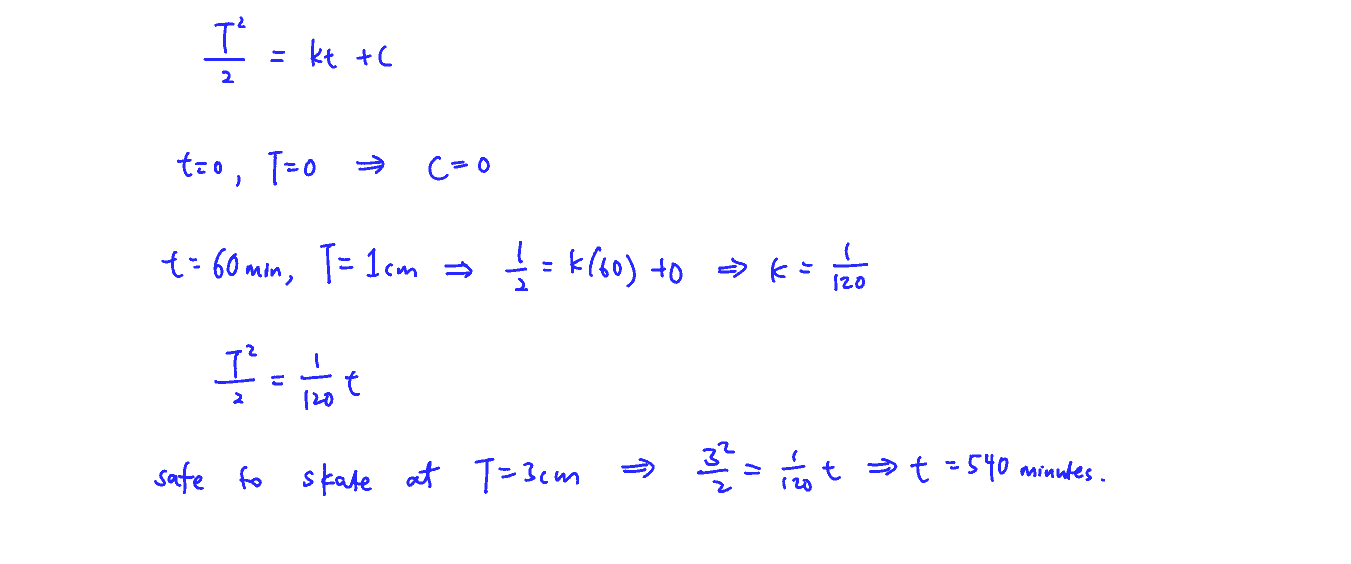
Share with your friends!
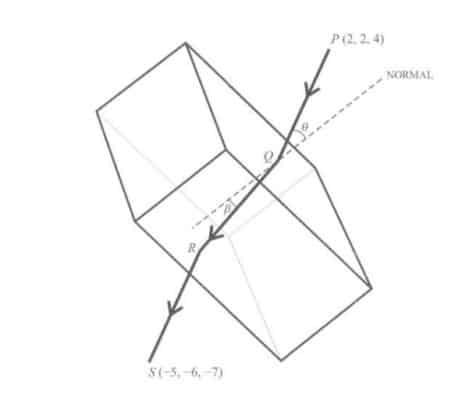
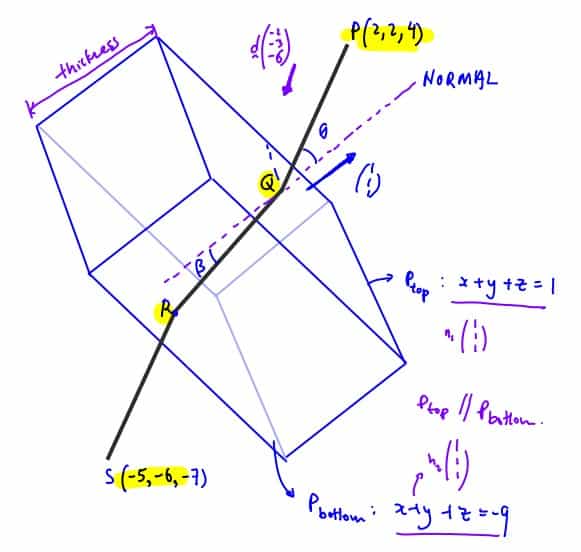
A ray of light passes from air into a material made into a rectangular prism. The ray of light is sent in direction $\left( \begin{matrix}-2 \\-3 \\ -6 \\\end{matrix} \right)$ from a light source at the point $P$ with coordinates $\left( 2,\,2,\,4 \right).$ The prism is placed so that the ray of light passes through the prism, entering at the point $Q$ and emerging at the point $R$ and is picked up by a sensor at point $S$ with coordinates $\left( -5,\,-6,\,-7 \right).$ The acute angle between $PQ$ and the normal to the top of the prism at $Q$ is $\theta $and the acute angle between $QR$ and the same normal is $\beta$ (see diagram).
It is given that the top of the prism is a part of the plane $x+y+z=1,$ and that the base of the prism is a part of the plane $x+y+z=-9.$ It is also given that the ray of light along $PQ$ is parallel to the ray of light along $RS$ so that $P,\,Q,\,R$ and $S$ lie in the same plane.
(i)
[5]
[5]
(ii)
[3]
[3]
(iii)
[3]
[3]
Snell’s law states that $\sin \theta =k\sin \beta$, where $k$ is a constant called the refractive index.
(iv)
[1]
[1]
(v)
[1]
[1]
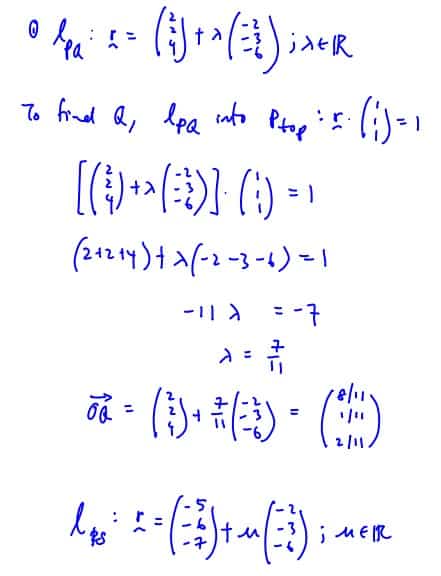
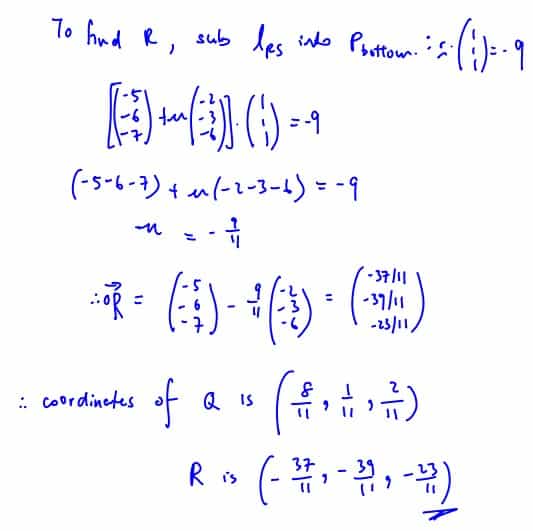

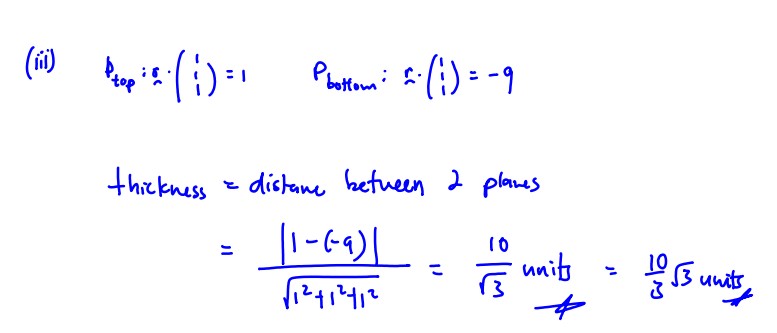
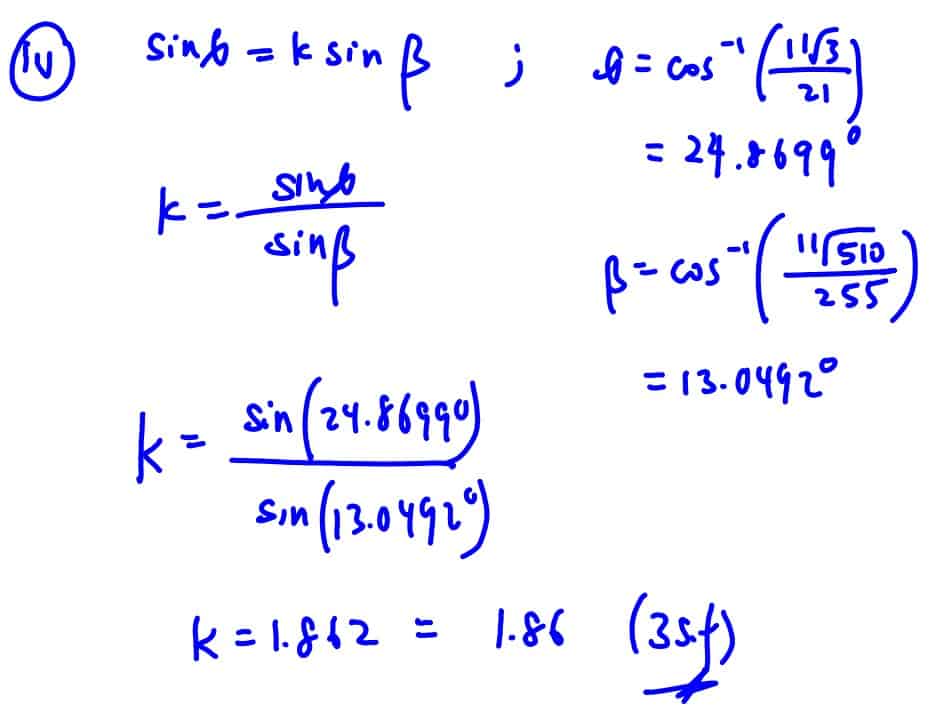
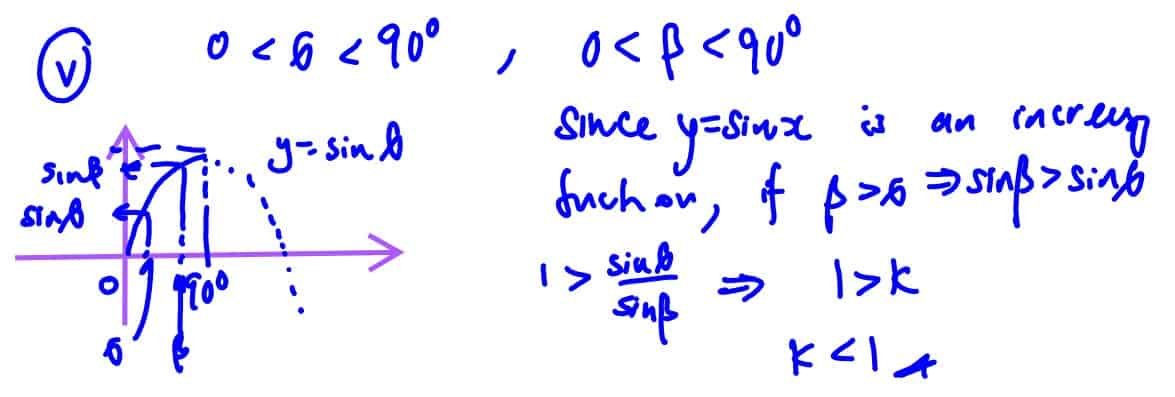

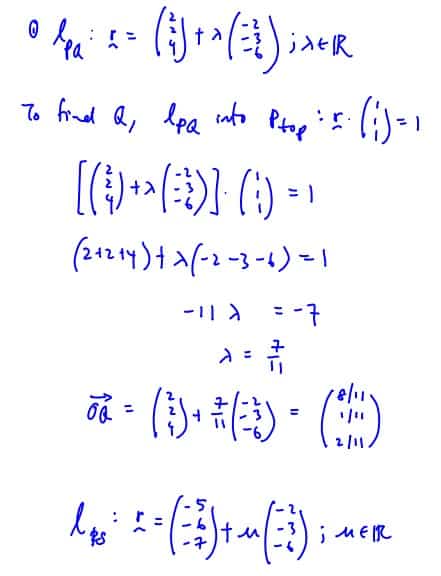
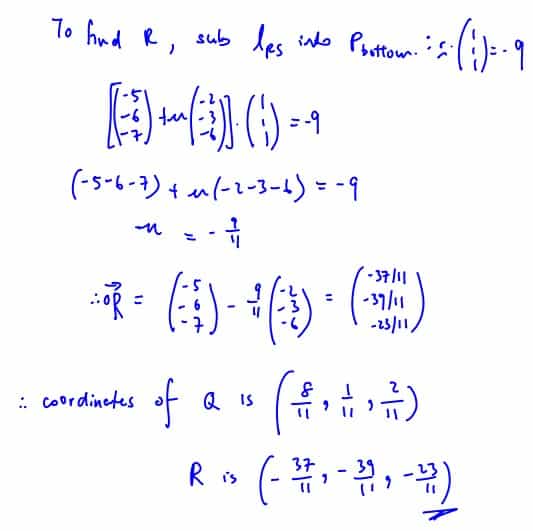

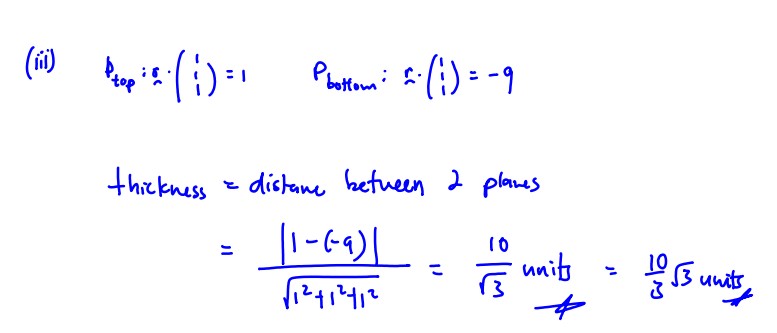
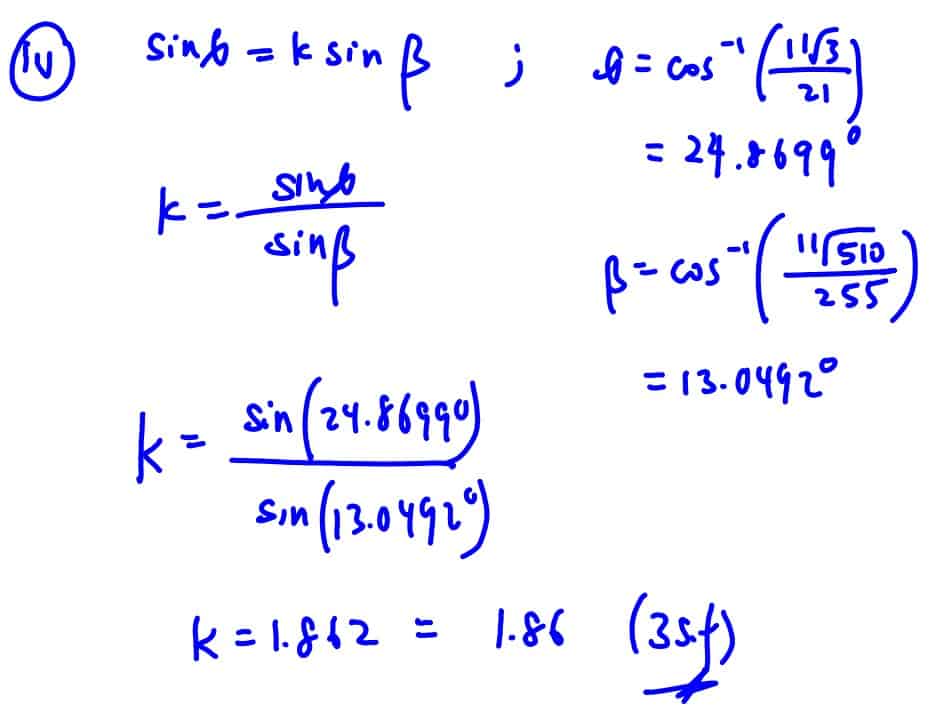
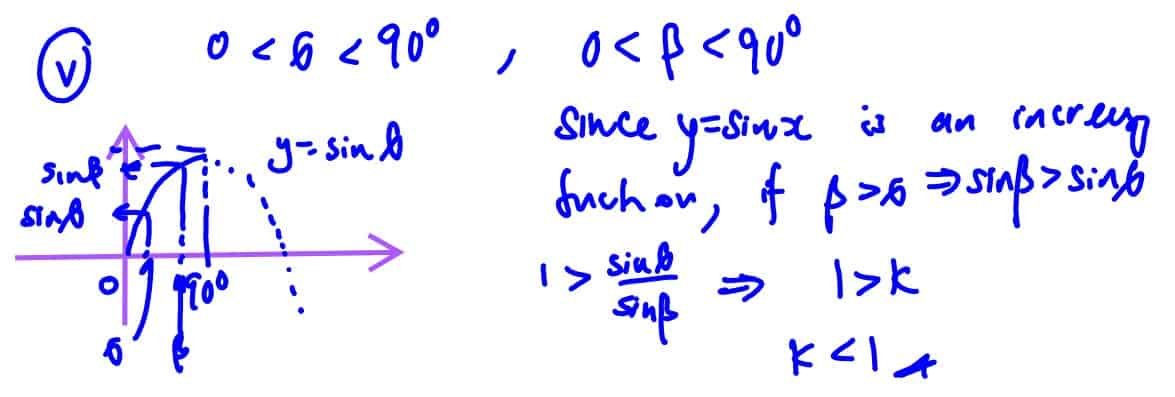
Share with your friends!
You are given that $I=\int{x{{\left( 1-x \right)}^{\frac{1}{2}}}}\text{d}x$.
(i)
Use integration by parts to find an expression for $I$.
[2]
(i) Use integration by parts to find an expression for $I$.
[2]
(ii)
Use the substitution ${{u}^{2}}=1-x$ to find another expression for $I$.
[2]
(ii) Use the substitution ${{u}^{2}}=1-x$ to find another expression for $I$.
[2]
(iii)
Show algebraically that your answers to parts (i) and (ii) differ by a constant.
[2]
(iii) Show algebraically that your answers to parts (i) and (ii) differ by a constant.
[2]
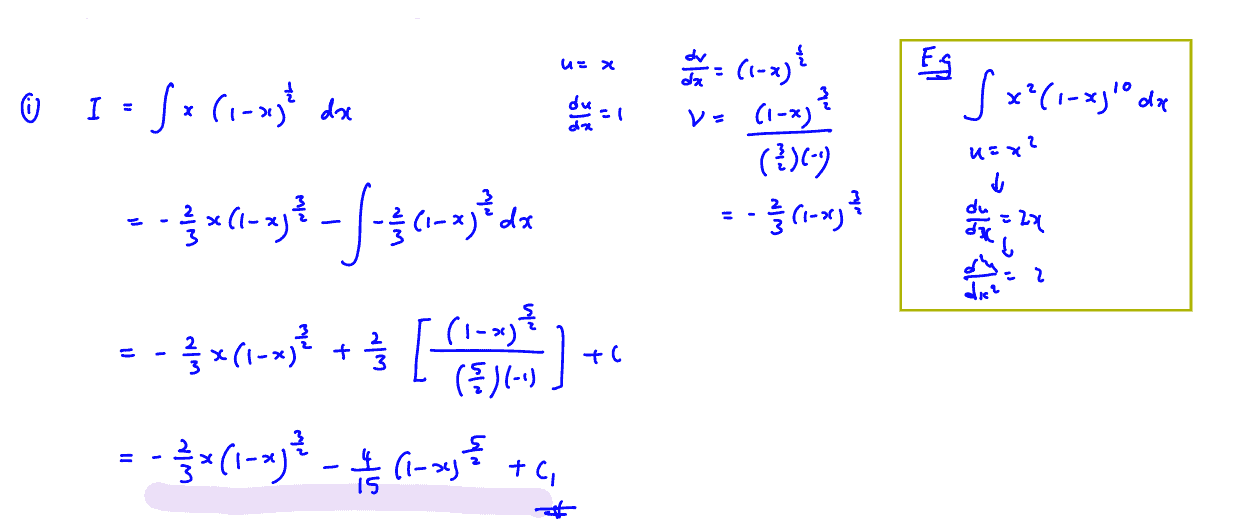
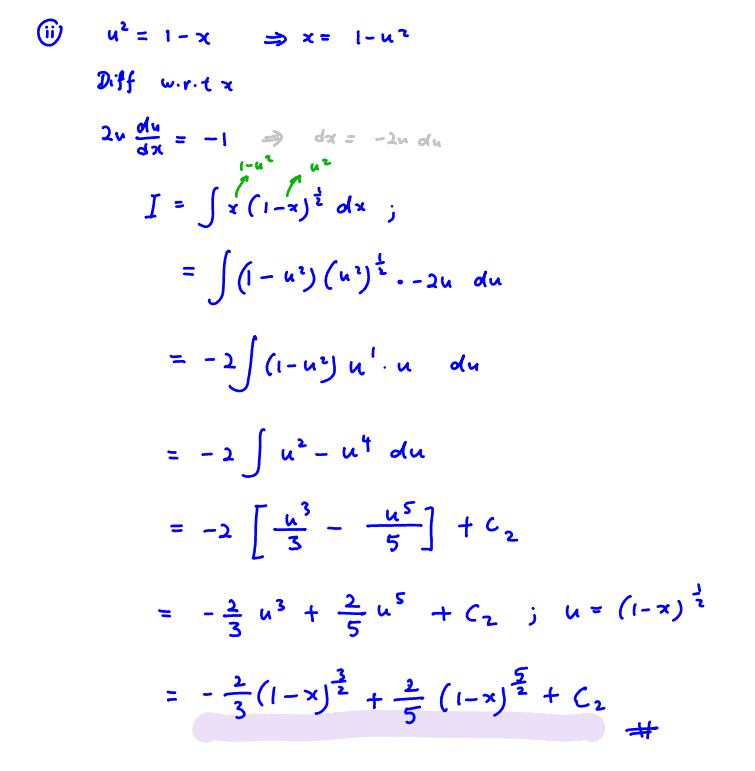
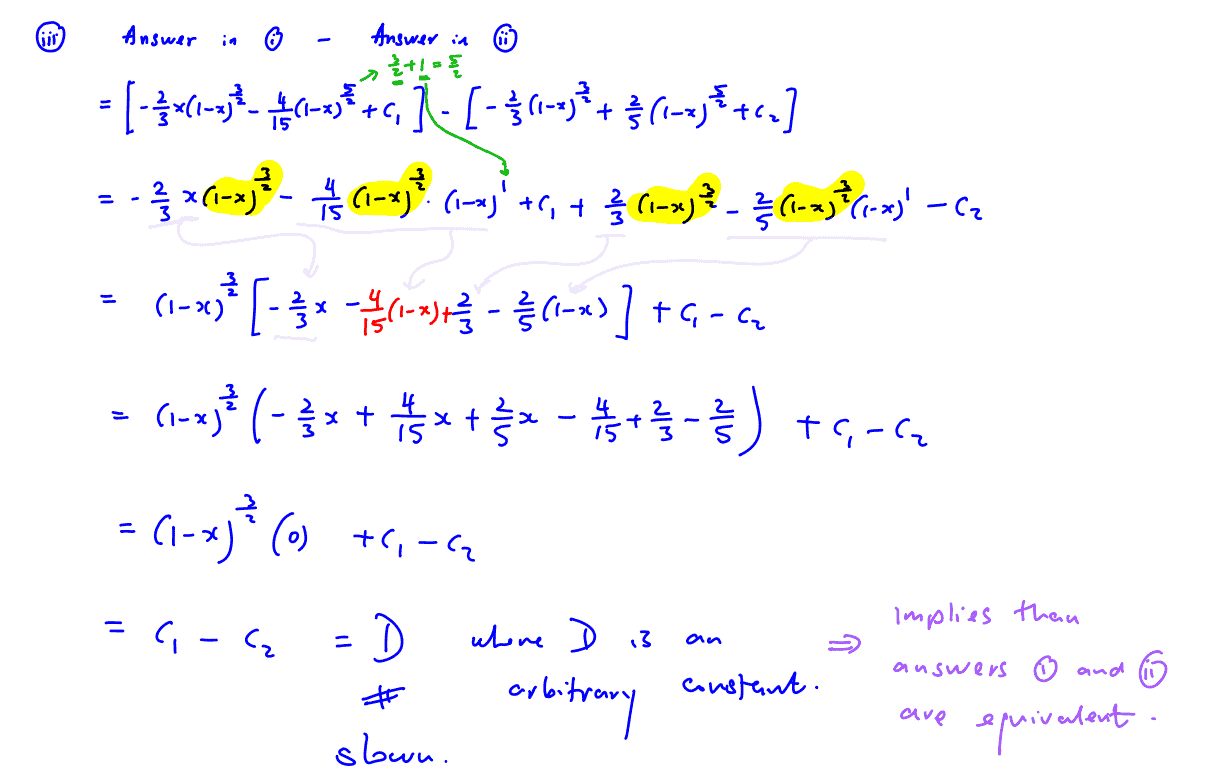
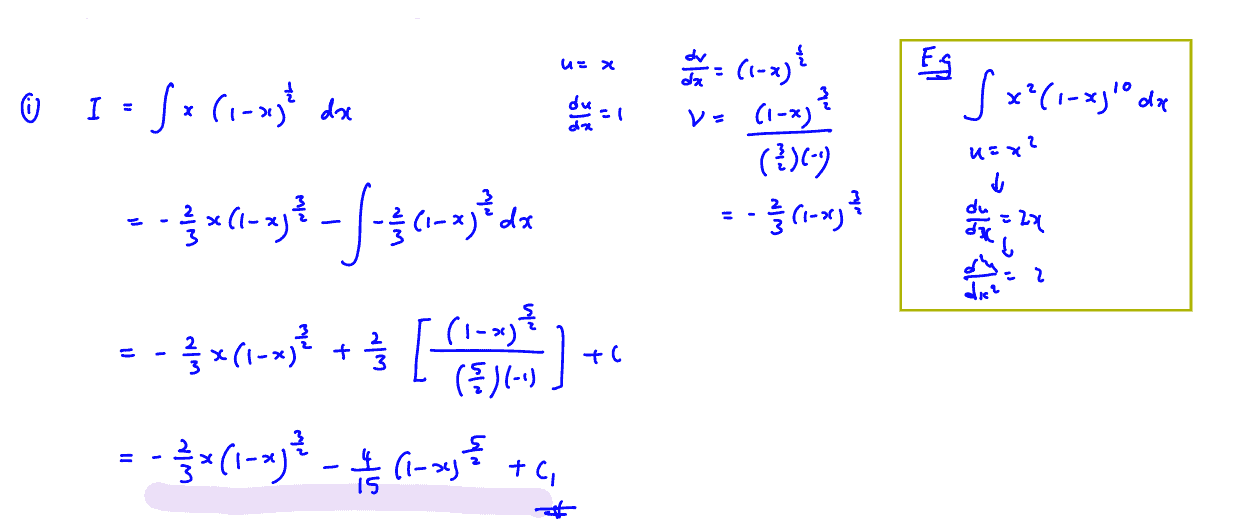
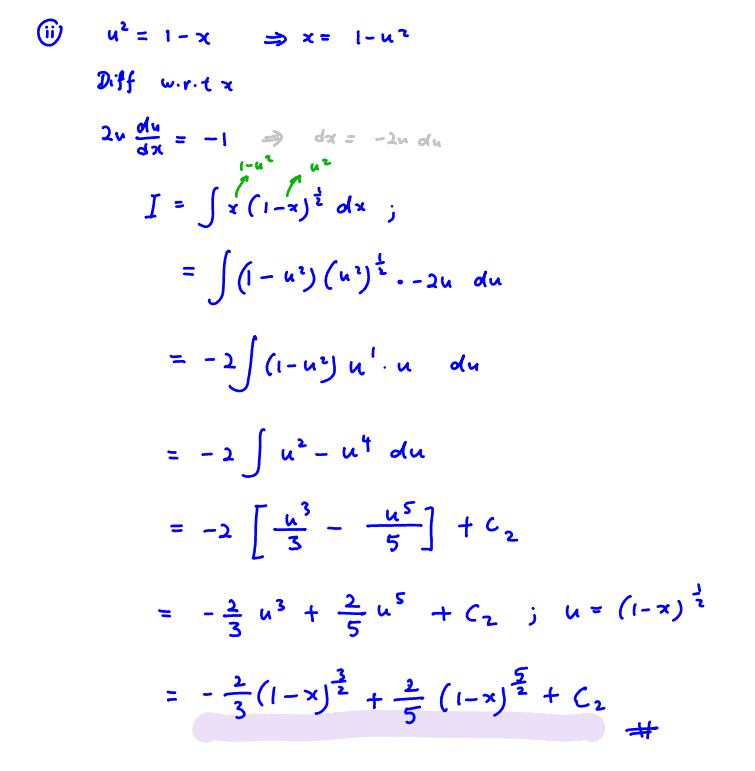
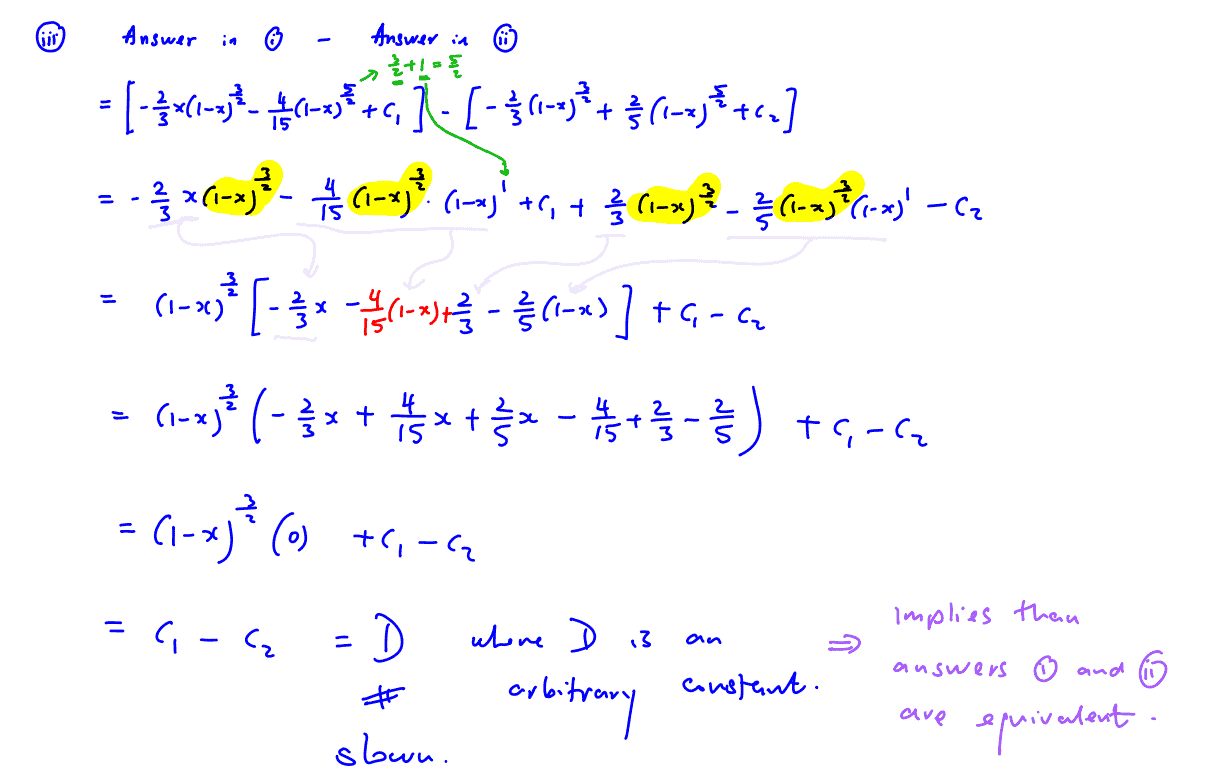
Share with your friends!
(i)
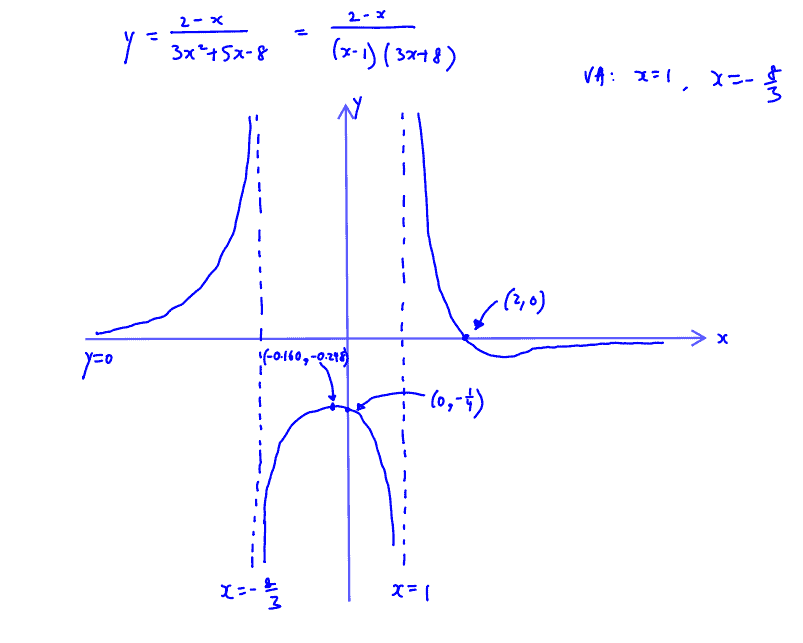
Sketch the graph of $y=\frac{2-x}{3{{x}^{2}}+5x-8}$. Give the equations of the asymptotes and the coordinates of the point(s) where the curve crosses either axis.
[4]
(i) Sketch the graph of $y=\frac{2-x}{3{{x}^{2}}+5x-8}$. Give the equations of the asymptotes and the coordinates of the point(s) where the curve crosses either axis.
[4]
(ii)
Solve the inequality $\frac{2-x}{3{{x}^{2}}+5x-8}>0$.
[1]
(ii) Solve the inequality $\frac{2-x}{3{{x}^{2}}+5x-8}>0$.
[1]
(iii)
Hence solve the inequality $\frac{x-2}{3{{x}^{2}}+5x-8}>0$.
[1]
(iii) Hence solve the inequality $\frac{x-2}{3{{x}^{2}}+5x-8}>0$.
[1]
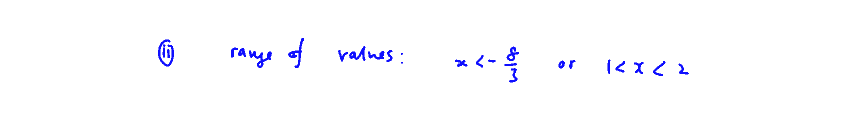
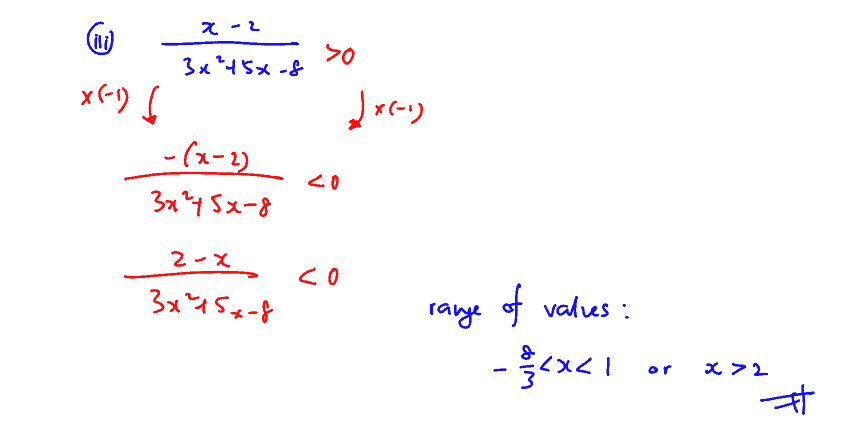

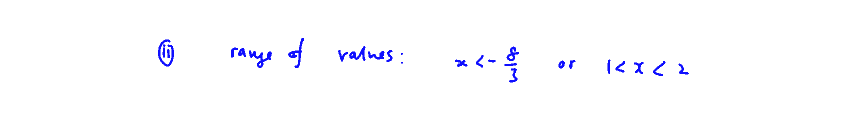
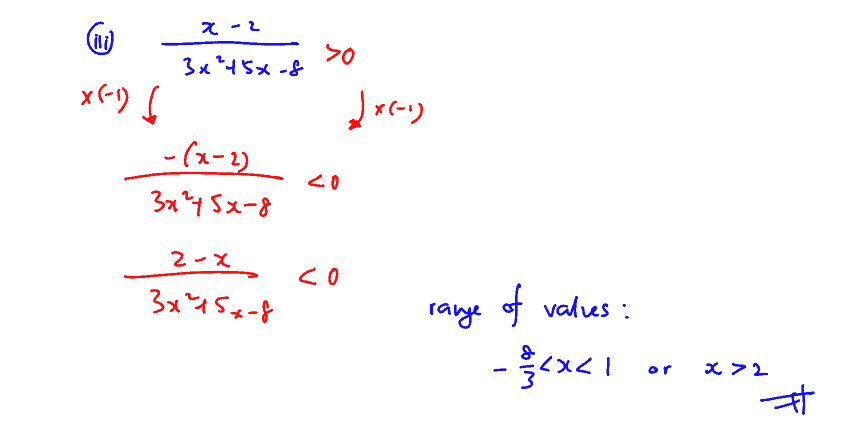
Share with your friends!
A solid cylinder has radius $r$ cm, height $h$ cm and total surface area $900$ cm$^{2}$. Find the exact value of the maximum possible volume of the cylinder. Find also the ratio $r:h$ that gives this maximum volume.
[7]
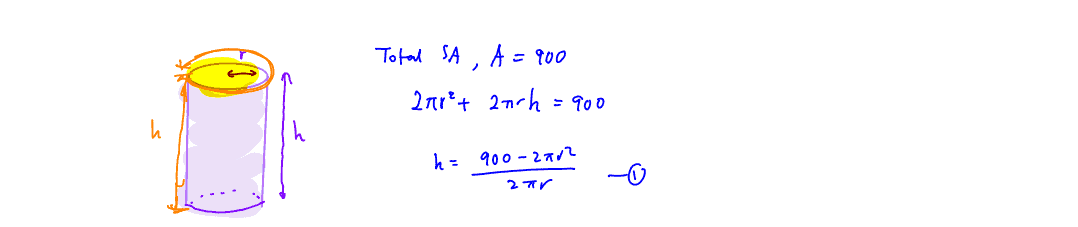
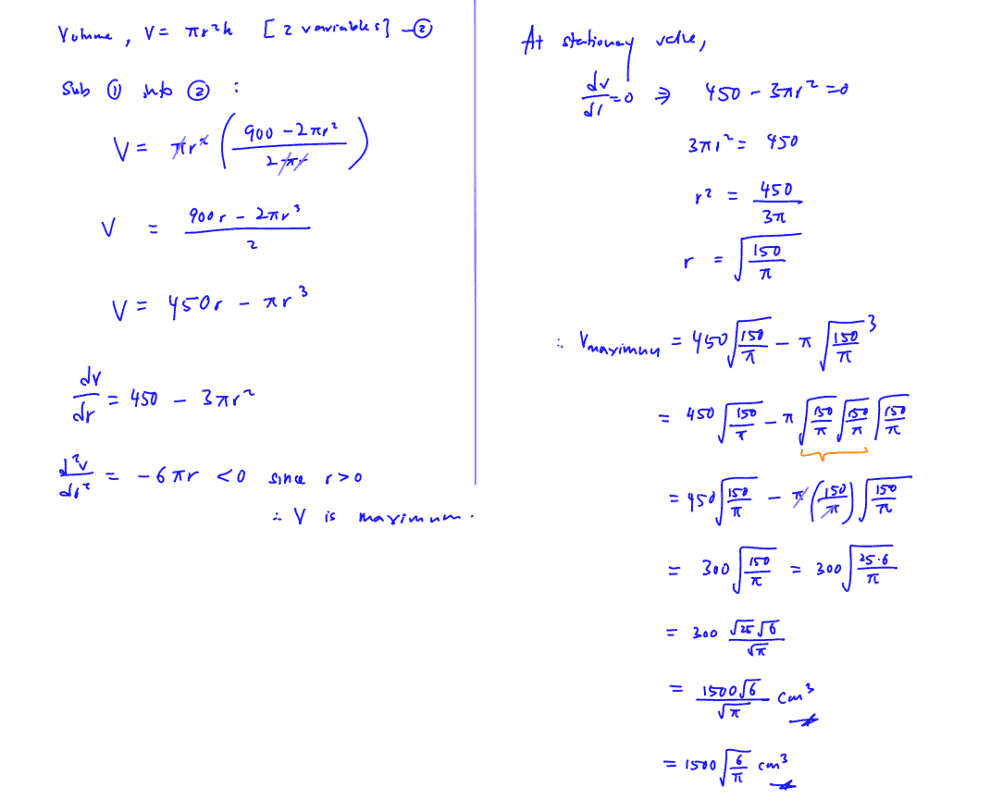
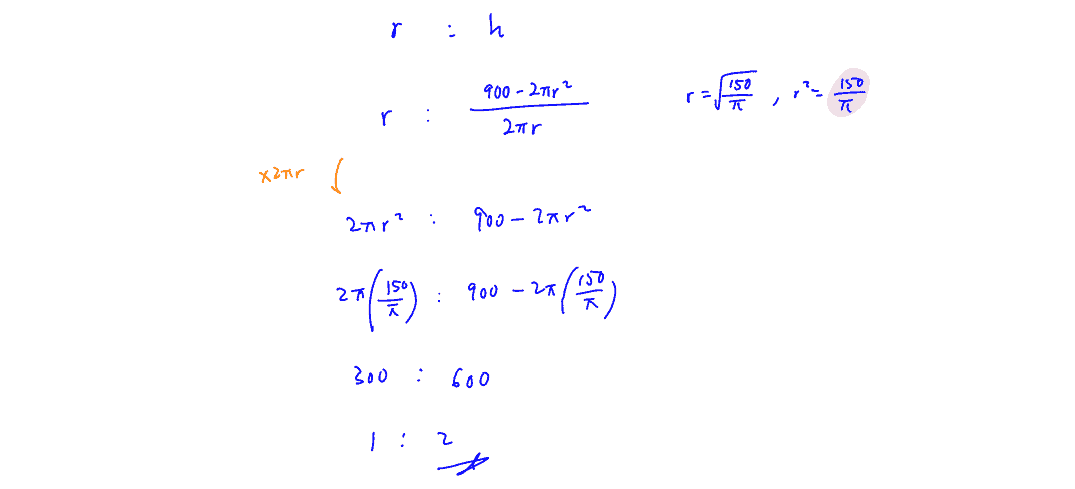
Share with your friends!
(i)
Given that $\text{f}\left( x \right)=\sec 2x$, find $\text{f}’\left( x \right)$ and $\text{f}”\left( x \right)$. Hence, or otherwise, find the Maclaurin series for $\text{f}\left( x \right)$, up to and including the term in ${{x}^{2}}$.
[5]
(i) Given that $\text{f}\left( x \right)=\sec 2x$, find $\text{f}’\left( x \right)$ and $\text{f}”\left( x \right)$. Hence, or otherwise, find the Maclaurin series for $\text{f}\left( x \right)$, up to and including the term in ${{x}^{2}}$.
[5]
(ii)
Use your series from part (i) to estimate $\int_{0}^{0.02}{\sec 2x\text{d}x}$, correct to $5$ decimal places.
[2]
(ii) Use your series from part (i) to estimate $\int_{0}^{0.02}{\sec 2x\text{d}x}$, correct to $5$ decimal places.
[2]
(iii)
Use your calculator to find $\int_{0}^{0.02}{\sec 2x\text{d}x}$, correct to $5$ decimal places.
[1]
(iii) Use your calculator to find $\int_{0}^{0.02}{\sec 2x\text{d}x}$, correct to $5$ decimal places.
[1]
(iv)
Comparing your answers to parts (ii) and (iii), and with reference to the value of $x$, comment on the accuracy of your approximations.
[2]
(iv) Comparing your answers to parts (ii) and (iii), and with reference to the value of $x$, comment on the accuracy of your approximations.
[2]
(v)
Explain why a Maclaurin series for $\text{g}\left( x \right)=\operatorname{cosec}2x$ cannot be found.
[1]
(v) Explain why a Maclaurin series for $\text{g}\left( x \right)=\operatorname{cosec}2x$ cannot be found.
[1]
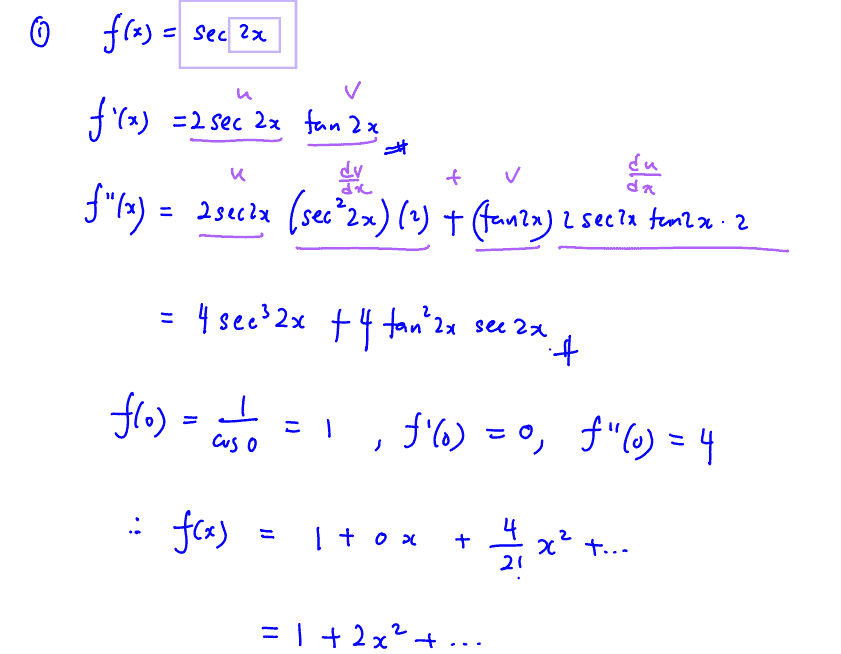
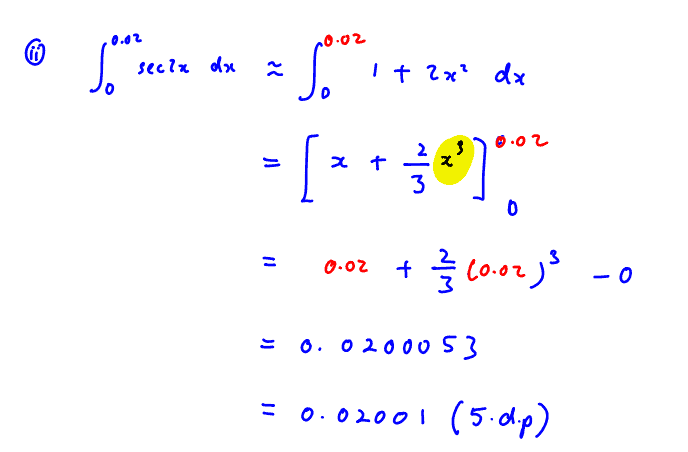
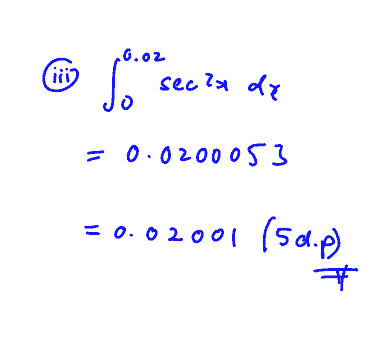

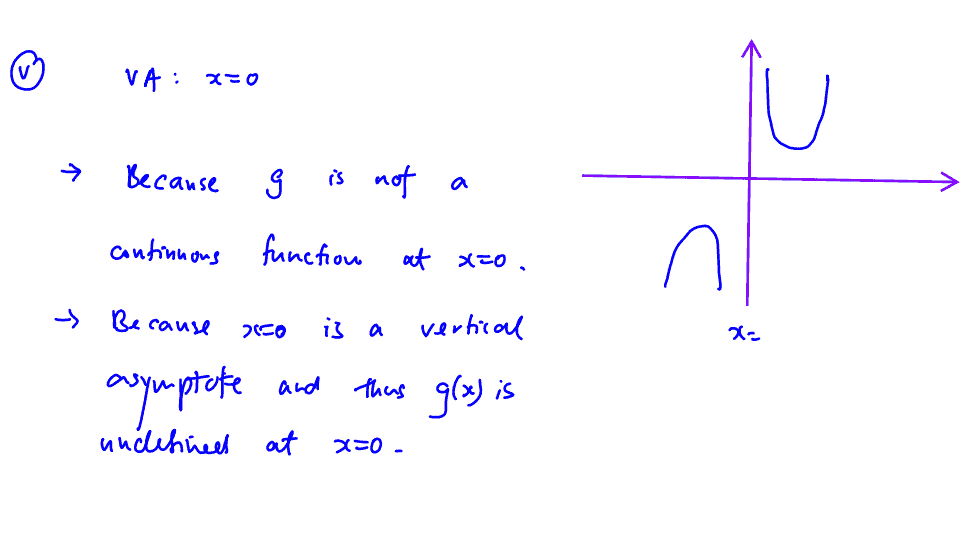
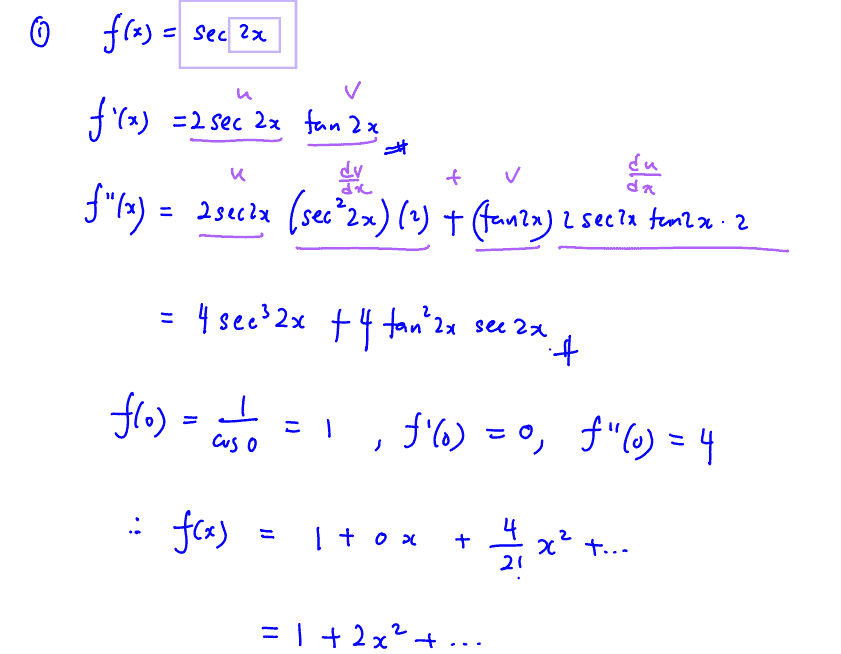
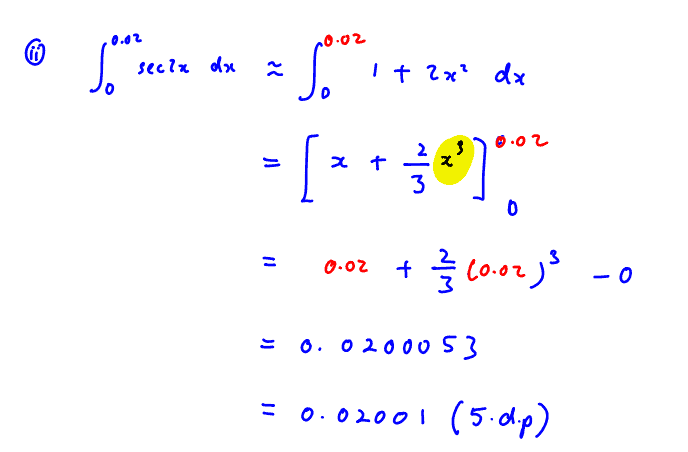
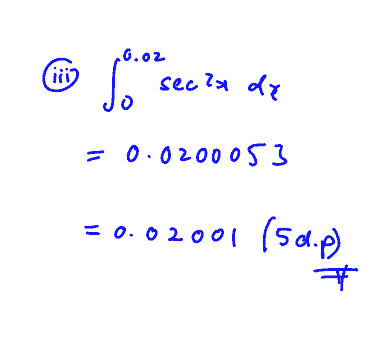

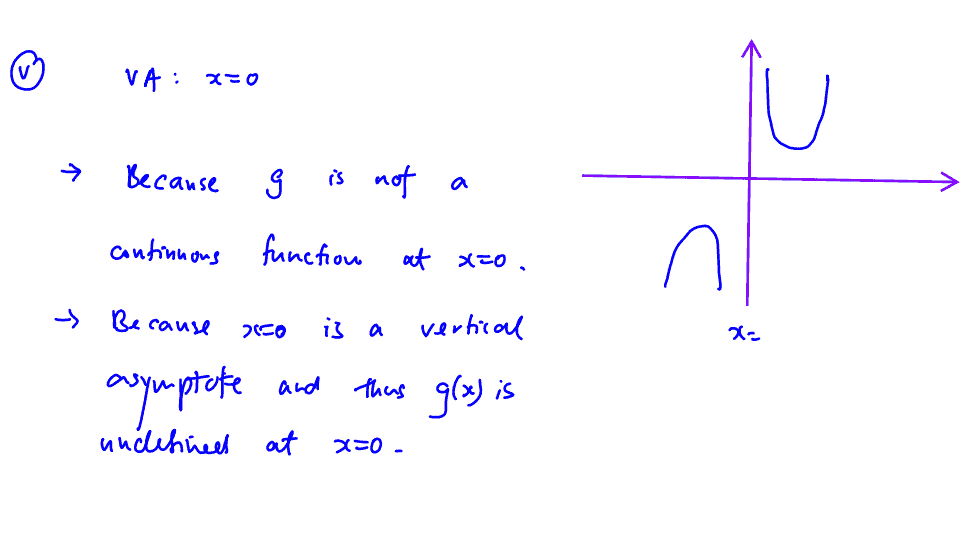
Share with your friends!
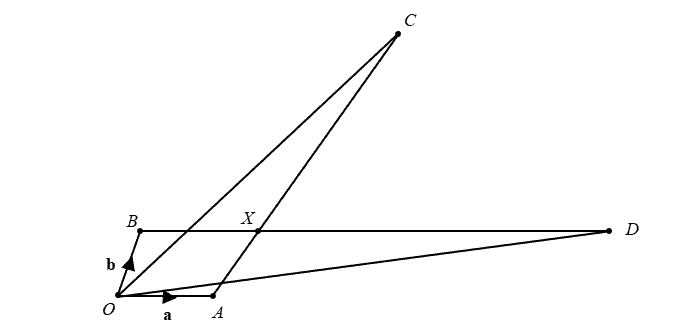
With reference to the origin $O,$ the points $A,\,B,\,C$ and $D$ are such that $\overrightarrow{OA}=\mathbf{a}\text{,}$$\overrightarrow{OB}=\mathbf{b}\text{,}$$\overrightarrow{OC}=2\mathbf{a}+4\mathbf{b}$and $\overrightarrow{OD}=\mathbf{b}+5\mathbf{a}\text{.}$ The lines $BD$ and $AC$ cross at $X$(see diagram).
(i)
[4]
[4]
The point $Y$ lies on $CD$ and is such that the points $O,\,X$ and $Y$ are collinear.
(ii)
[6]
[6]
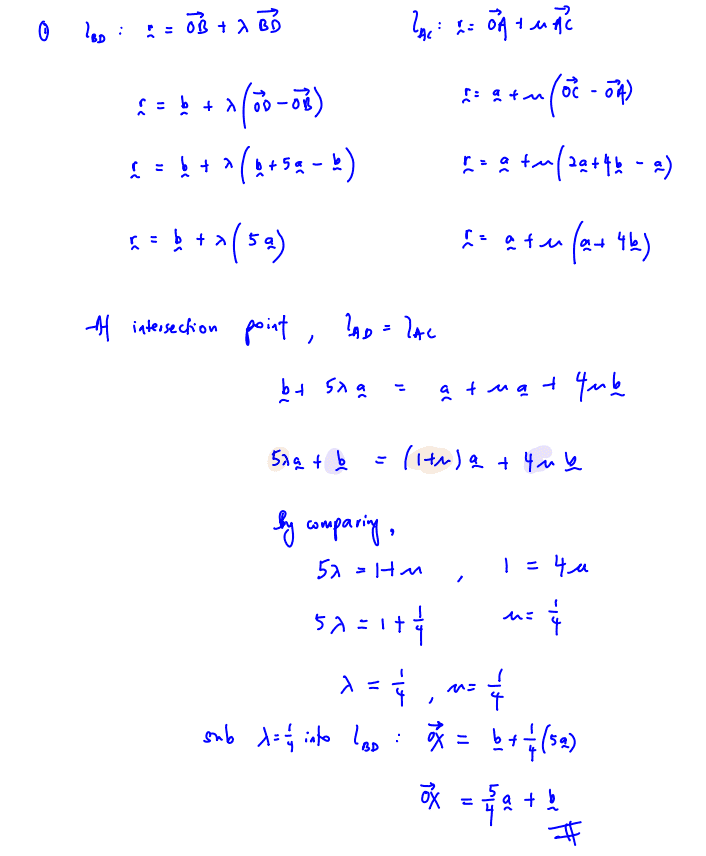
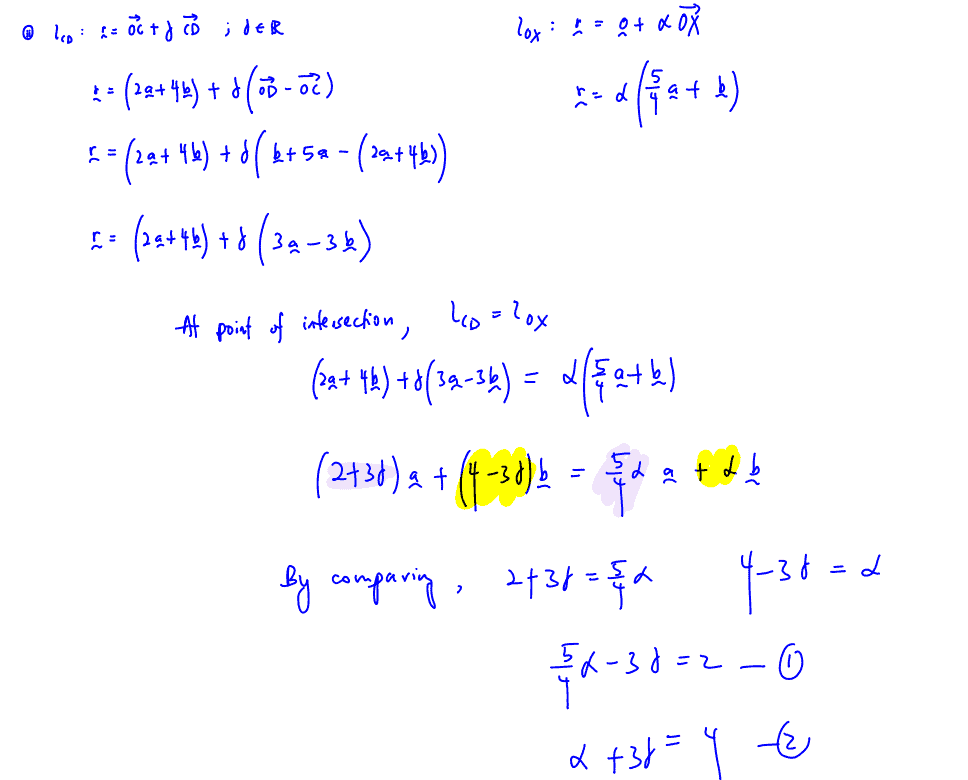
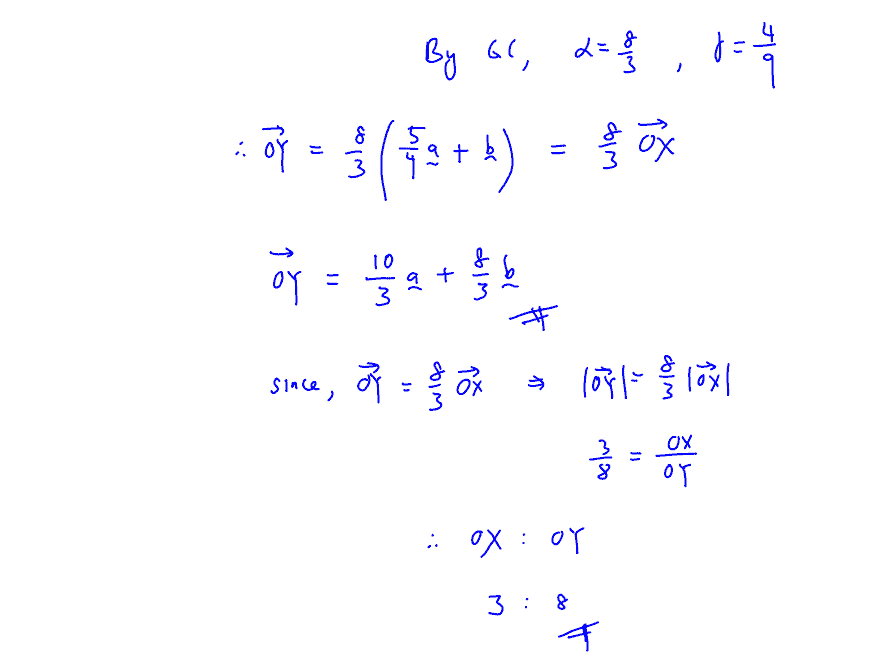
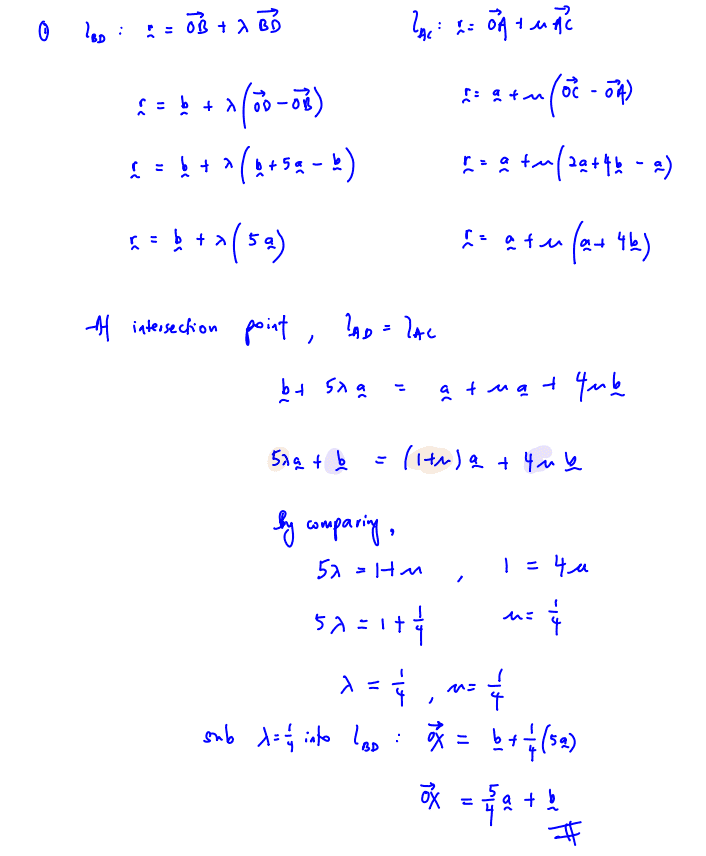
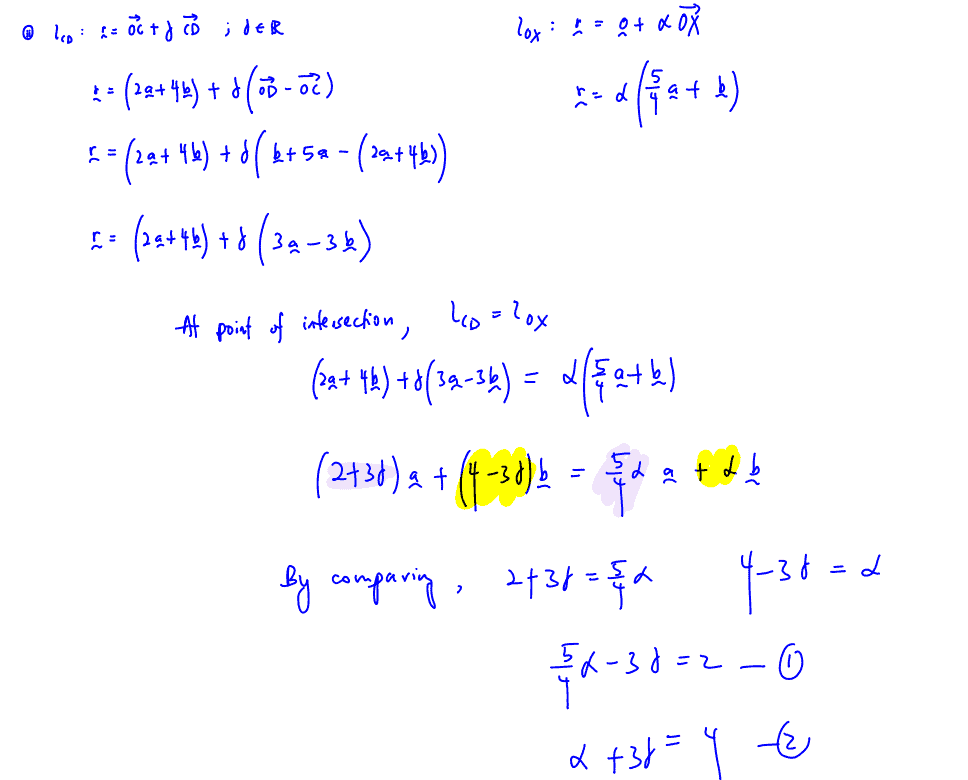
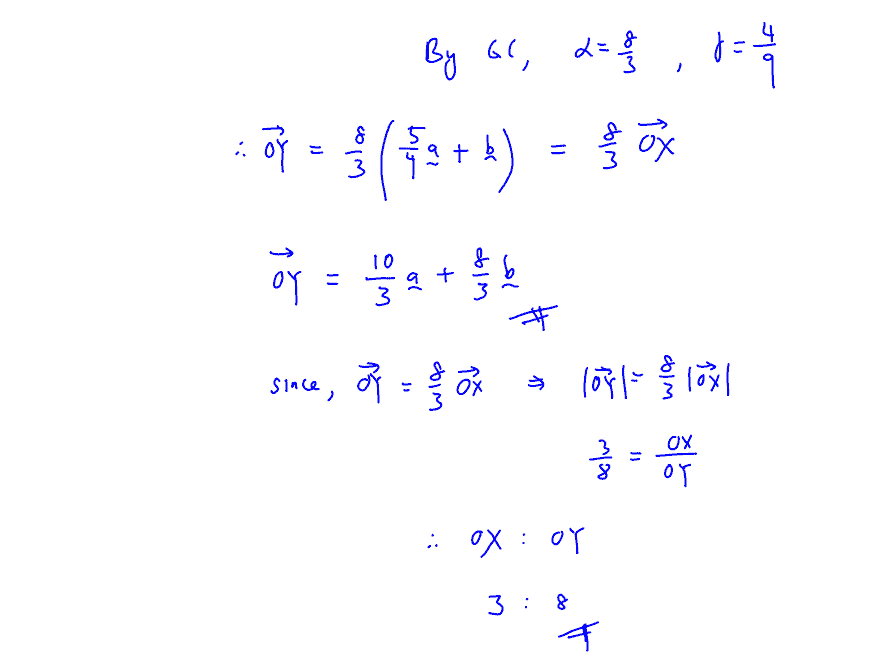
Share with your friends!
A company produces drinking mugs. It is known that, on average, $8\%$ of the mugs are faulty. Each day the quality manager collects $50$ of the mugs at random and checks them; the number of faulty mugs found is the random variable $F$.
(i)
State, in the context of the question, two assumptions needed to model $F$ by a binomial distribution.
[2]
(i) State, in the context of the question, two assumptions needed to model $F$ by a binomial distribution.
[2]
You are now given that $F$ can be modelled by a binomial distribution.
(ii)
Find the probability that, on a randomly chosen day, at least $7$ faulty mugs are found.
[2]
(ii) Find the probability that, on a randomly chosen day, at least $7$ faulty mugs are found.
[2]
(iii)
The number of faulty mugs produced each day is independent of other days. Find the probability that, in a randomly chosen working week of $5$ days, at least $7$ faulty mugs are found on no more than $2$ days.
[2]
(iii) The number of faulty mugs produced each day is independent of other days. Find the probability that, in a randomly chosen working week of $5$ days, at least $7$ faulty mugs are found on no more than $2$ days.
[2]
The company also makes saucers. The number of faulty saucers also follows a binomial distribution. The probability that a saucer is faulty is $p$. Faults on saucers are independent of faults on mugs.
(iv)
Write down an expression in terms of $p$ for the probability that, in a random sample of $10$ saucers, exactly $2$ are faulty.
[1]
(iv) Write down an expression in terms of $p$ for the probability that, in a random sample of $10$ saucers, exactly $2$ are faulty.
[1]
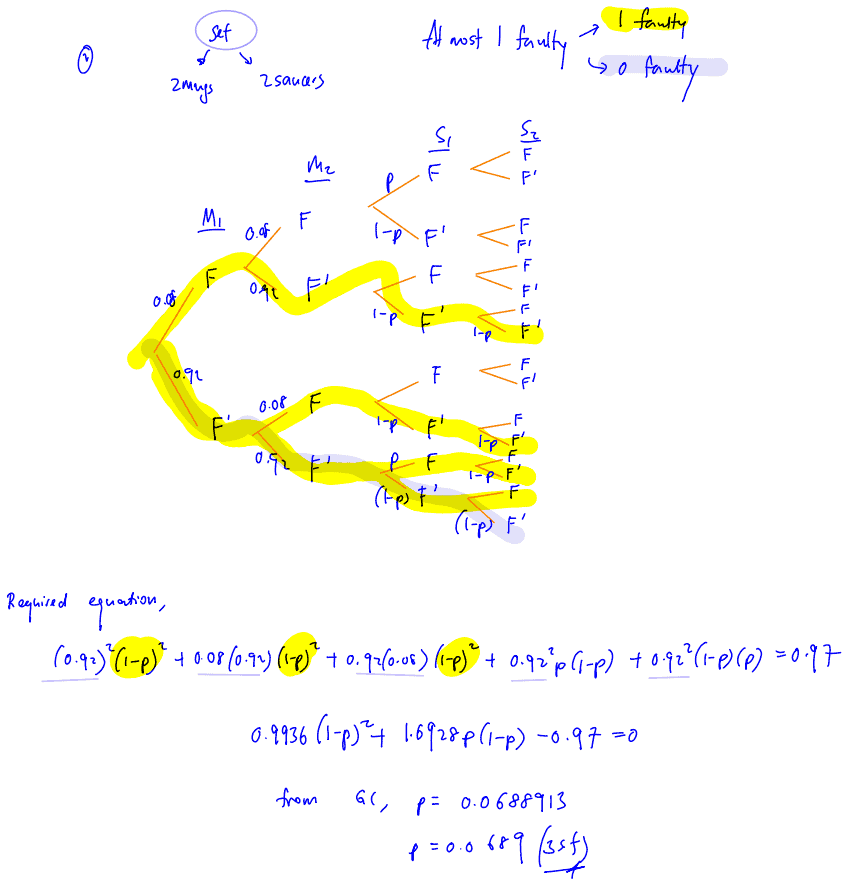
The mugs and saucers are sold in sets of $2$ randomly chosen mugs and $2$ randomly chosen saucers. The probability that a set contains at most $1$ faulty item is $0.97$.
(v)
Write down an equation satisfied by $p$. Hence find the value of $p$.
[4]
(v) Write down an expression in terms of $p$ for the probability that, in a random sample of $10$ saucers, exactly $2$ are faulty.
[1]
Assumptions:
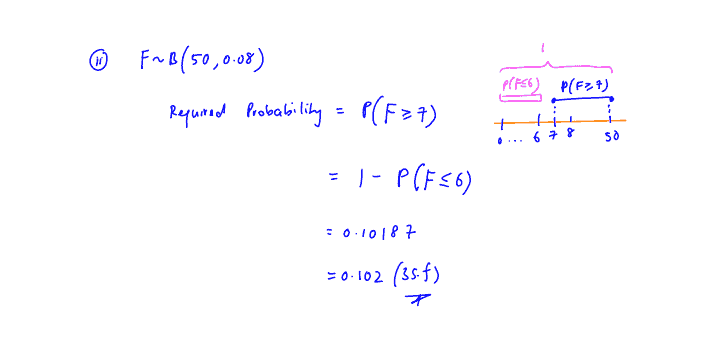
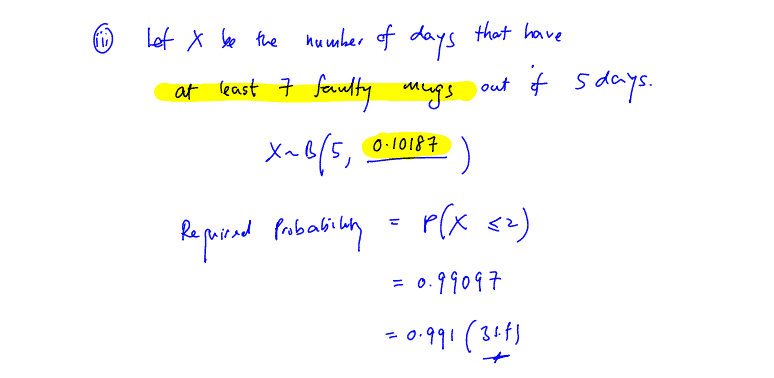
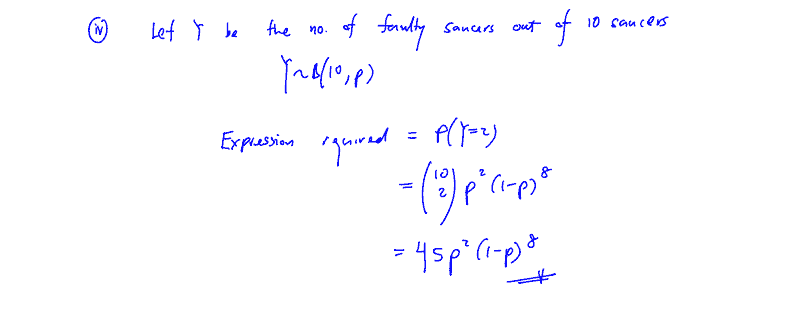
Assumptions:
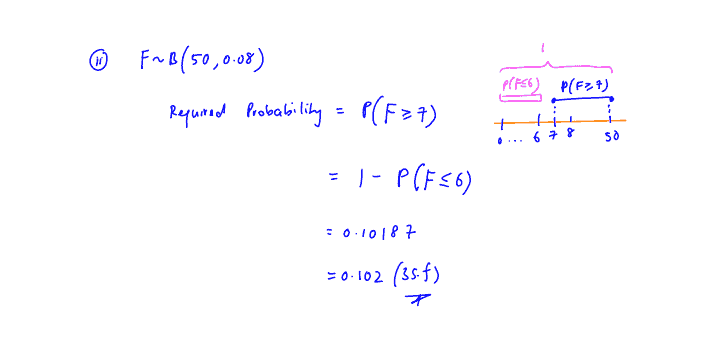
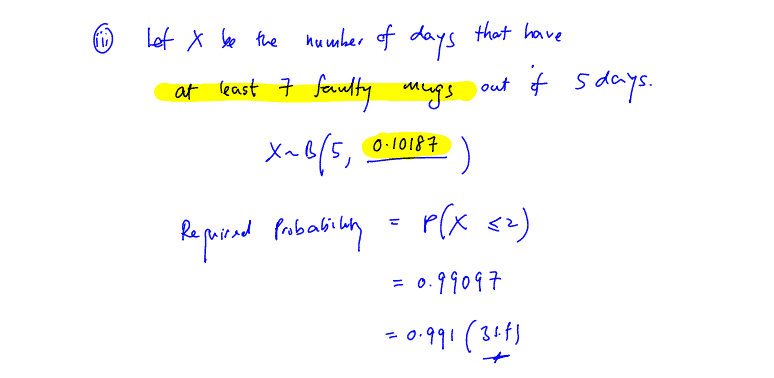
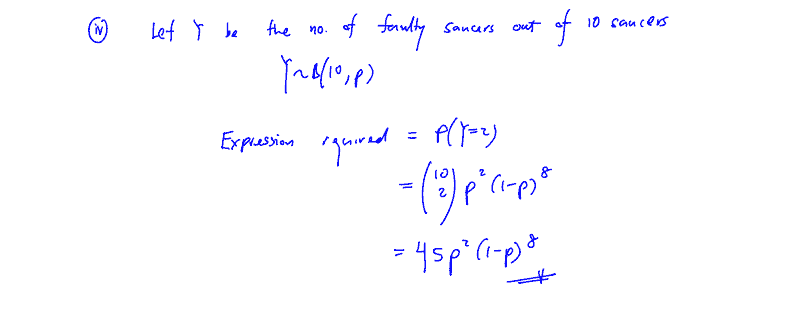

Share with your friends!

In the ever-evolving landscape of education, where academic success is often measured by performance in exams, the need for effective test preparation has never been

What is the MF 27? The MF 27, set to replace the MF 26 from 2025, is a comprehensive formula sheet developed by the Ministry

As you approach the final hours before your exam, remember that a balanced approach is key. A light review can keep the information fresh in
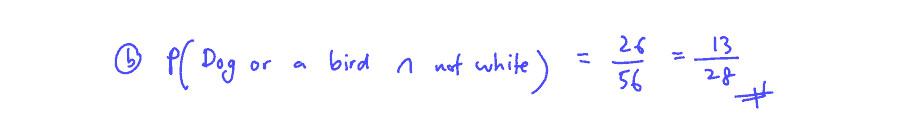
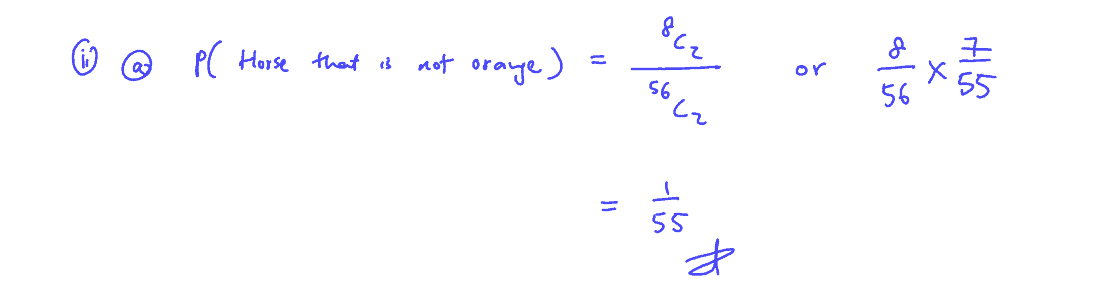


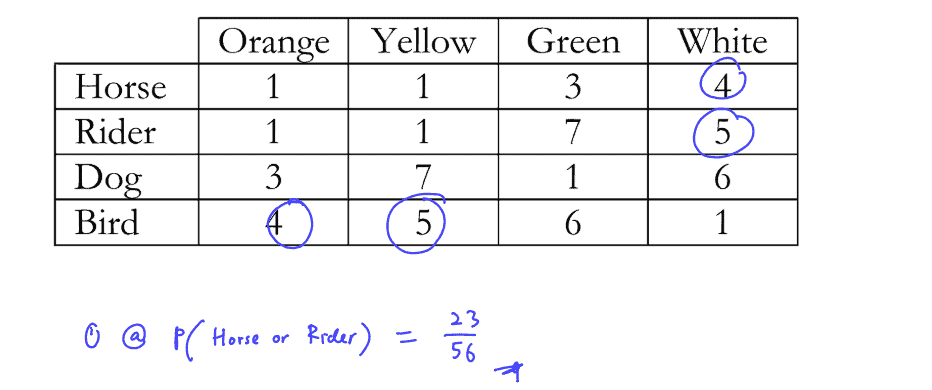
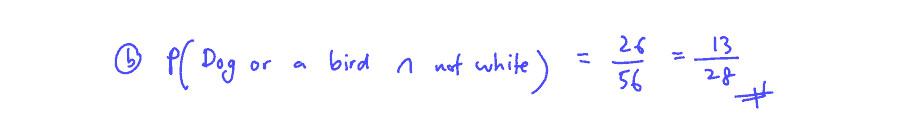
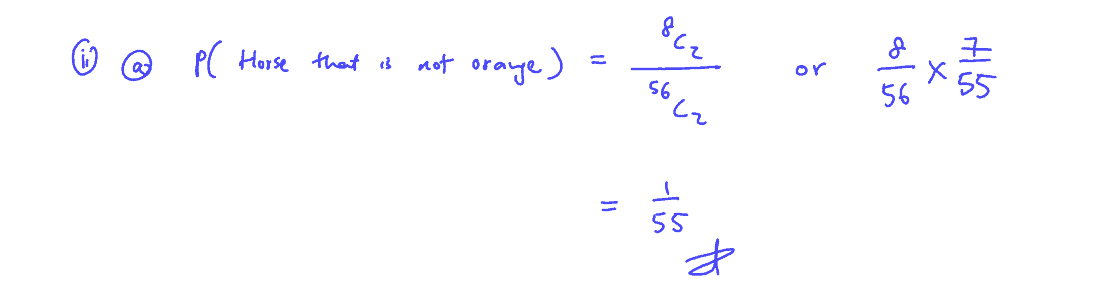


Share with your friends!