- Home
- Study Guides
Basic Rules of Definite Integral
Have you ever been asked to calculate an area? If you are given a rectangle and want to know the area, it’s easy: multiply its width time its length. Trouble is, what if you have irregular shapes or shapes with complicated boundaries? You could try to figure out the area by breaking the shape into a lot of little rectangles and adding up the areas. But here is a better way — the definite integral.
The definite integral is a powerful concept used to represent the area under a curve, which turns out to be useful in a lot of calculations. The definite integral is continuous on a closed interval $[a,b]$, in other words, it has start and end values. In this section, we will learn some basic rules of the definite integral.
$\int_{b}^{a}{\text{f}(x)\text{ d}x}=\text{F}(a)-\text{F}(b)$
Practice Question 1
Evaluate the following.
(a)
$\int_{1}^{6}{3x-1\,\text{d}x}$
(a) $\int_{1}^{6}{3x-1\,\text{d}x}$
(b)
$\int_{2}^{4}{\frac{3}{{{x}^{4}}}+1\,\text{d}x}$
(b) $\int_{2}^{4}{\frac{3}{{{x}^{4}}}+1\,\text{d}x}$
(c)
$\int_{1}^{6}{\sqrt{x+3}\,\text{d}x}$
(c) $\int_{1}^{6}{\sqrt{x+3}\,\text{d}x}$
- (a)
- (b)
- (c)
$\begin{aligned}
& \int_{1}^{6}{3x\text{d}x} \\
& =\left[ \frac{3{{x}^{2}}}{2}-x \right]_{1}^{6} \\
& =\left[ \frac{3}{2}{{\left( 6 \right)}^{2}}-6 \right]-\left[ \frac{3{{\left( 1 \right)}^{2}}}{2}-1 \right] \\
& =48-\frac{1}{2} \\
& =\frac{95}{2} \\
\end{aligned}$
$\begin{aligned}
& \int_{2}^{4}{\frac{3}{{{x}^{4}}}+1\text{d}x} \\
& =\int_{2}^{4}{3{{x}^{-4}}+1\,\text{d}x} \\
& =\left[ \frac{3{{x}^{-3}}}{\left( -3 \right)}+x \right]_{2}^{4} \\
& =\left[ -\frac{1}{{{x}^{3}}}+x \right]_{2}^{4} \\
& =\left[ -\frac{1}{{{4}^{3}}}+4 \right]-\left[ -\frac{1}{{{2}^{3}}}+2 \right] \\
& =\frac{255}{64}-\left( \frac{15}{8} \right) \\
& =\frac{135}{64} \\
\end{aligned}$
$\begin{aligned}
& \int_{1}^{6}{\sqrt{x+3}\text{d}x} \\
& =\int_{1}^{6}{{{\left( x+3 \right)}^{\frac{1}{2}}}\text{d}x} \\
& =\left[ \frac{1{{\left( x+3 \right)}^{\frac{3}{2}}}}{\frac{3}{2}} \right]_{1}^{6} \\
& =\frac{2}{3}\left[ {{\sqrt{x+3}}^{3}} \right]_{1}^{6} \\
& =\frac{2}{3}\left[ \left( {{\sqrt{6+3}}^{3}} \right)-\left( {{\sqrt{1+3}}^{3}} \right) \right] \\
& =\frac{2}{3}\left[ {{\sqrt{9}}^{3}}-{{\sqrt{4}}^{3}} \right] \\
& =\frac{2}{3}\left( {{3}^{3}}-{{2}^{3}} \right) \\
& =\frac{38}{3} \\
\end{aligned}$
- (a)
- (b)
- (c)
$\begin{aligned}
& \int_{1}^{6}{3x\text{d}x} \\
& =\left[ \frac{3{{x}^{2}}}{2}-x \right]_{1}^{6} \\
& =\left[ \frac{3}{2}{{\left( 6 \right)}^{2}}-6 \right]-\left[ \frac{3{{\left( 1 \right)}^{2}}}{2}-1 \right] \\
& =48-\frac{1}{2} \\
& =\frac{95}{2} \\
\end{aligned}$
$\begin{aligned}
& \int_{2}^{4}{\frac{3}{{{x}^{4}}}+1\text{d}x} \\
& =\int_{2}^{4}{3{{x}^{-4}}+1\,\text{d}x} \\
& =\left[ \frac{3{{x}^{-3}}}{\left( -3 \right)}+x \right]_{2}^{4} \\
& =\left[ -\frac{1}{{{x}^{3}}}+x \right]_{2}^{4} \\
& =\left[ -\frac{1}{{{4}^{3}}}+4 \right]-\left[ -\frac{1}{{{2}^{3}}}+2 \right] \\
& =\frac{255}{64}-\left( \frac{15}{8} \right) \\
& =\frac{135}{64} \\
\end{aligned}$
$\begin{aligned}
& \int_{1}^{6}{\sqrt{x+3}\text{d}x} \\
& =\int_{1}^{6}{{{\left( x+3 \right)}^{\frac{1}{2}}}\text{d}x} \\
& =\left[ \frac{1{{\left( x+3 \right)}^{\frac{3}{2}}}}{\frac{3}{2}} \right]_{1}^{6} \\
& =\frac{2}{3}\left[ {{\sqrt{x+3}}^{3}} \right]_{1}^{6} \\
& =\frac{2}{3}\left[ \left( {{\sqrt{6+3}}^{3}} \right)-\left( {{\sqrt{1+3}}^{3}} \right) \right] \\
& =\frac{2}{3}\left[ {{\sqrt{9}}^{3}}-{{\sqrt{4}}^{3}} \right] \\
& =\frac{2}{3}\left( {{3}^{3}}-{{2}^{3}} \right) \\
& =\frac{38}{3} \\
\end{aligned}$
Understanding Results of Definite Integral
Now let’s look at some interesting properties of the definite integral.
If we reverse the direction of the interval, we would get the original integral in the negative direction.
$\int_{b}^{a}{\text{f}\left( x \right)\text{d}x}=-\int_{a}^{b}{\text{f}\left( x \right)\text{d}x}$
We can also add integrals of two adjacent intervals together.
$\int_{a}^{c}{\text{f}\left( x \right)\text{d}x}=\int_{a}^{b}{\text{f}\left( x \right)\text{d}x}+\int_{b}^{c}{\text{f}\left( x \right)\text{d}x}$
Practice Question 2
Given that $\int_{-2}^{5}{\text{f}\left( x \right)\text{ d}x}=14$, find
(a)
$\int_{-2}^{5}{\text{3f}\left( x \right)\,\,\text{d}x}$
(a) $\int_{-2}^{5}{\text{3f}\left( x \right)\,\,\text{d}x}$
(b)
$\int_{5}^{-2}{\left[ \text{f}\left( x \right)-3x \right]\text{ d}x}$
(b) $\int_{5}^{-2}{\left[ \text{f}\left( x \right)-3x \right]\text{ d}x}$
- (a)
- (b)
$\begin{aligned}
& \int_{-2}^{5}{\text{3f}\left( x \right)\text{d}x} \\
& =3\int_{-2}^{5}{\text{f}\left( x \right)\text{d}x} \\
& =3\times 14 \\
& =42 \\
\end{aligned}$
$\begin{aligned}
& \int_{5}^{-2}{\left[ \text{f}\left( x \right)-3x \right]\text{ d}x} \\
& =\int_{5}^{-2}{\text{f}\left( x \right)\text{d}x}-\int_{5}^{-2}{3x\,\text{d}x} \\
& =-\int_{-2}^{5}{\text{f}\left( x \right)\text{d}x}-\left[ \frac{3{{x}^{2}}}{2} \right]_{5}^{-2} \\
& =-14-\left[ \frac{3}{2}{{\left( -2 \right)}^{2}}-\frac{3}{2}{{\left( 5 \right)}^{2}} \right] \\
& =-14-\left( -\frac{63}{2} \right) \\
& =\frac{35}{2} \\
\end{aligned}$
- (a)
- (b)
$\begin{aligned}
& \int_{-2}^{5}{\text{3f}\left( x \right)\text{d}x} \\
& =3\int_{-2}^{5}{\text{f}\left( x \right)\text{d}x} \\
& =3\times 14 \\
& =42 \\
\end{aligned}$
$\begin{aligned}
& \int_{5}^{-2}{\left[ \text{f}\left( x \right)-3x \right]\text{ d}x} \\
& =\int_{5}^{-2}{\text{f}\left( x \right)\text{d}x}-\int_{5}^{-2}{3x\,\text{d}x} \\
& =-\int_{-2}^{5}{\text{f}\left( x \right)\text{d}x}-\left[ \frac{3{{x}^{2}}}{2} \right]_{5}^{-2} \\
& =-14-\left[ \frac{3}{2}{{\left( -2 \right)}^{2}}-\frac{3}{2}{{\left( 5 \right)}^{2}} \right] \\
& =-14-\left( -\frac{63}{2} \right) \\
& =\frac{35}{2} \\
\end{aligned}$
Definite Integration as the Reverse of Differentiation
In calculus, the definite integral can be defined as the reverse of differentiation. That makes sense: if we know how to differentiate, we can integrate; and if we know how to integrate, we can work out what a derivative is. In this section, we will see how this concept applies in solving questions.
Practice Question 3
Differentiate $x\cos 3x$ with respect to $x$. Hence, show that $\int_{0}^{\frac{\pi }{9}}{x\sin 3x\text{ d}x}=\frac{\sqrt{3}}{18}-\frac{\pi }{54}$.
- Differentiate
- Show
$\begin{aligned}
& \frac{\text{d}}{\text{d}x}\left( x\cos 3x \right) \\
& =x\left[ -\sin 3x\cdot 3 \right]+\left[ \cos 3x \right]\cdot 1 \\
& =-3x\sin 3x+\cos 3x \\
\end{aligned}$
$\begin{aligned}
\int_{0}^{\frac{\pi }{9}}{-3x\sin 3x}+\cos 3x\,\text{d}x&=\left[ x\cos 3x \right]_{0}^{\frac{\pi }{9}} \\
-3\int_{0}^{\frac{\pi }{9}}{x\sin 3x\,\text{d}x}+\int_{0}^{\frac{\pi }{9}}{\cos 3xdx}&=\frac{\pi }{9}\cos 3\left( \frac{\pi }{9} \right)-0\cos 0 \\
-3\int_{0}^{\frac{\pi }{9}}{x\sin 3x\,\text{d}x}+\left[ \frac{\sin 3x}{3} \right]_{0}^{\frac{\pi }{9}}&=\frac{\pi }{9}\cos \frac{\pi }{3} \\
-3\int_{0}^{\frac{\pi }{9}}{x\sin 3x\,\text{d}x}+\left[ \frac{\sin \frac{\pi }{3}}{3}-\frac{\sin 0}{3} \right]&=\frac{\pi }{9}\left( \frac{1}{2} \right) \\
-3\int_{0}^{\frac{\pi }{9}}{x\sin 3x\,\text{d}x}+\frac{\frac{\sqrt{3}}{2}}{3}&=\frac{\pi }{18} \\
-3\int_{0}^{\frac{\pi }{9}}{x\sin 3x\,\text{d}x}&=\frac{\pi }{18}-\frac{\sqrt{3}}{6} \\
-3\int_{0}^{\frac{\pi }{9}}{x\sin 3x\,\text{d}x}&=-\frac{1}{3}\left[ \frac{\pi }{18}-\frac{\sqrt{3}}{6} \right] \\
& =\frac{\sqrt{3}}{18}-\frac{\pi }{54}
\end{aligned}$
Finding the Equation of the Curve
The idea behind integration is that if we have a curve (or a function) and we know one of its points (or values), then integrating gives us the equation of the curve.
Practice Question 4
A curve passes through the point $\left( -2,\frac{1}{2} \right)$ and has gradient given by $\frac{\text{d}y}{\text{d}x}={{\left( 2x+1 \right)}^{2}}$. Find the equation of the curve.
- Solution
$\begin{aligned}
& \frac{\text{d}y}{\text{d}x}={{\left( 2x+1 \right)}^{2}} \\
& y=\int{{{\left( 2x+1 \right)}^{2}}\text{d}x} \\
& y=\frac{{{\left( 2x+1 \right)}^{3}}}{3\left( 2 \right)}+c \\
& y=\frac{1}{6}{{\left( 2x+1 \right)}^{3}}+c
\end{aligned}$
When $x=-2,y=\frac{1}{2}$:
$\begin{aligned}
\frac{1}{2}&=\frac{1}{6}{{\left( 2\left( -2 \right)+1 \right)}^{3}}+c \\
\frac{1}{2}&=\frac{1}{6}{{\left( -3 \right)}^{3}}+c \\
\frac{1}{2}&=-\frac{9}{2}+c \\
c&=\frac{1}{2}+\frac{9}{2}=5
\end{aligned}$
Equation of curve: $y=\frac{1}{6}{{\left( 2x+1 \right)}^{3}}+5$
- Solution
$\begin{aligned}
& \frac{\text{d}y}{\text{d}x}={{\left( 2x+1 \right)}^{2}} \\
& y=\int{{{\left( 2x+1 \right)}^{2}}\text{d}x} \\
& y=\frac{{{\left( 2x+1 \right)}^{3}}}{3\left( 2 \right)}+c \\
& y=\frac{1}{6}{{\left( 2x+1 \right)}^{3}}+c
\end{aligned}$
When $x=-2,y=\frac{1}{2}$:
$\begin{aligned}
\frac{1}{2}&=\frac{1}{6}{{\left( 2\left( -2 \right)+1 \right)}^{3}}+c \\
\frac{1}{2}&=\frac{1}{6}{{\left( -3 \right)}^{3}}+c \\
\frac{1}{2}&=-\frac{9}{2}+c \\
c&=\frac{1}{2}+\frac{9}{2}=5
\end{aligned}$
Equation of curve: $y=\frac{1}{6}{{\left( 2x+1 \right)}^{3}}+5$
Finding the Equation of the Curve from Second Derivative
The equation of the curve can also be found from the second derivative using integration. This takes a little longer but it gives you practice with derivatives and integrals. Let’s have a look at the practice question.
Practice Question 5
At any point $(x,y)$ on a curve, $\frac{{{\text{d}}^{2}}y}{\text{d}{{x}^{2}}}=\frac{18}{{{\left( x-2 \right)}^{3}}}$. The gradient of the curve at $\left( 5,20 \right)$ is $2$.
Find the equation of the tangent to the curve when it cuts the $y$- axis.
- Image
- I
- II
- III
Part 1: Finding the Original Equation of the Curve
$\begin{aligned}
\frac{\text{d}y}{\text{d}x}&=\int{18{{\left( x-2 \right)}^{-3}}\text{d}x} \\
& =\frac{18{{\left( x-2 \right)}^{-2}}}{\left( -2 \right)}+c \\
\frac{\text{d}y}{\text{d}x}&=-9{{\left( x-2 \right)}^{-2}}+c
\end{aligned}$
Solve for the $c$
When $\frac{\text{d}y}{\text{d}x}=2,x=5$:
$\begin{aligned}
2&=-9{{\left( 5-2 \right)}^{-2}}+c \\
c&=2+9{{\left( 3 \right)}^{-2}} \\
& =3
\end{aligned}$
$\frac{\text{d}y}{\text{d}x}=-9{{\left( x-2 \right)}^{-2}}+3$
Part 2: Finding the Equation of the Line
$\begin{aligned}
y&=\int{-9{{\left( x-2 \right)}^{-2}}+3\,\text{d}x} \\
y&=\frac{-9{{\left( x-2 \right)}^{-1}}}{\left( -1 \right)}+3x+D \\
y&=\frac{9}{x-2}+3x+D
\end{aligned}$
Substitute coordinates into the equation
When $x=5,y=20$:
$\begin{aligned}
20&=\frac{9}{5-2}+3\left( 5 \right)+D \\
D&=2
\end{aligned}$
Equation of curve $y=\frac{9}{x-2}+3x+2$
Part 3: Find the $y$-intercept, when $x=0$
$\begin{aligned}
y&=\frac{9}{0-2}+3\left( 0 \right)+2 \\
y&=-\frac{5}{2}
\end{aligned}$
$\left( 0,-\frac{5}{2} \right)$
Find the gradient of the tangent
$\begin{aligned}
{{m}_{\operatorname{t}\text{angent}}},{{\left. \frac{\text{d}y}{\text{d}x} \right|}_{x=0}}&=-9{{\left( 0-2 \right)}^{-2}}+3 \\
& =\frac{3}{4}
\end{aligned}$
Find the equation of the tangent
$\begin{aligned}
y-\left( -\frac{5}{2} \right)&=\frac{3}{4}\left( x-0 \right) \\
y&=\frac{3}{4}x-\frac{5}{2}
\end{aligned}$
- Image
- I
- II
- III
Part 1: Finding the Original Equation of the Curve
$\begin{aligned}
\frac{\text{d}y}{\text{d}x}&=\int{18{{\left( x-2 \right)}^{-3}}\text{d}x} \\
& =\frac{18{{\left( x-2 \right)}^{-2}}}{\left( -2 \right)}+c \\
\frac{\text{d}y}{\text{d}x}&=-9{{\left( x-2 \right)}^{-2}}+c
\end{aligned}$
Solve for the $c$
When $\frac{\text{d}y}{\text{d}x}=2,x=5$:
$\begin{aligned}
2&=-9{{\left( 5-2 \right)}^{-2}}+c \\
c&=2+9{{\left( 3 \right)}^{-2}} \\
& =3
\end{aligned}$
$\frac{\text{d}y}{\text{d}x}=-9{{\left( x-2 \right)}^{-2}}+3$
Part 2: Finding the Equation of the Line
$\begin{aligned}
y&=\int{-9{{\left( x-2 \right)}^{-2}}+3\,\text{d}x} \\
y&=\frac{-9{{\left( x-2 \right)}^{-1}}}{\left( -1 \right)}+3x+D \\
y&=\frac{9}{x-2}+3x+D
\end{aligned}$
Substitute coordinates into the equation
When $x=5,y=20$:
$\begin{aligned}
20&=\frac{9}{5-2}+3\left( 5 \right)+D \\
D&=2
\end{aligned}$
Equation of curve $y=\frac{9}{x-2}+3x+2$
Part 3: Find the $y$-intercept, when $x=0$
$\begin{aligned}
y&=\frac{9}{0-2}+3\left( 0 \right)+2 \\
y&=-\frac{5}{2}
\end{aligned}$
$\left( 0,-\frac{5}{2} \right)$
Find the gradient of the tangent
$\begin{aligned}
{{m}_{\operatorname{t}\text{angent}}},{{\left. \frac{\text{d}y}{\text{d}x} \right|}_{x=0}}&=-9{{\left( 0-2 \right)}^{-2}}+3 \\
& =\frac{3}{4}
\end{aligned}$
Find the equation of the tangent
$\begin{aligned}
y-\left( -\frac{5}{2} \right)&=\frac{3}{4}\left( x-0 \right) \\
y&=\frac{3}{4}x-\frac{5}{2}
\end{aligned}$
Practice Question 6
Problems involving Unknowns
The curve for which $\frac{\text{d}y}{\text{d}x}\,\,=\,\frac{a}{{{(2x\,+\,3\,)}^{3}}}\,\,-\,\,1\,,\,$where $a$ is a constant, is such that the tangent to the curve at $\left( -1,0 \right)$ is perpendicular to the line $5y=x+1$. Find the value of $a$ and the equation of the curve.
- I
- II
The gradient at $x=-1$ is perpendicular to the gradient of the line.
Finding the gradient of the line:
$\begin{aligned}
y&=\frac{1}{5}x+\frac{1}{5} \\
{{m}_{\text{line}}}&=\frac{1}{5}
\end{aligned}$
Finding the value of $a$:
$\begin{aligned}
{{m}_{\text{tangent}}}&={{\left. \frac{\text{d}y}{\text{d}x} \right|}_{x=-1}} \\
& =\frac{a}{{{\left( 2\left( -1 \right)+3 \right)}^{3}}}-1 \\
& =a-1
\end{aligned}$
Since they are perpendicular to each other,
$\begin{aligned}
{{m}_{\text{tangent}}}\times {{m}_{\text{line}}}&=-1 \\
\left( a-1 \right)\times \frac{1}{5}&=-1 \\
a-1&=-5 \\
a&=-4
\end{aligned}$
Finding the equation of the curve:
$\begin{aligned}
\frac{\text{d}y}{\text{d}x}&=-\frac{4}{{{\left( 2x+3 \right)}^{3}}}-1 \\
y&=\int{-4{{\left( 2x+3 \right)}^{-3}}-1\,\text{d}x} \\
y&=\frac{-4{{\left( 2x+3 \right)}^{-2}}}{\left( -2 \right)\left( 2 \right)}-x+c \\
y&={{\left( 2x+3 \right)}^{-2}}-x+c
\end{aligned}$
Find the value of constant $c$:
When $x=-1,y=0$:
$\begin{aligned}
0&={{\left( -2+3 \right)}^{-2}}-\left( -1 \right)+c \\
0&=1+1+c \\
c&=-2
\end{aligned}$
$\therefore y={{\left( 2x+3 \right)}^{-2}}-x-2$
Equation of curve, $y=\frac{1}{{{\left( 2x+3 \right)}^{2}}}-x-2$
- I
- II
The gradient at $x=-1$ is perpendicular to the gradient of the line.
Finding the gradient of the line:
$\begin{aligned}
y&=\frac{1}{5}x+\frac{1}{5} \\
{{m}_{\text{line}}}&=\frac{1}{5}
\end{aligned}$
Finding the value of $a$:
$\begin{aligned}
{{m}_{\text{tangent}}}&={{\left. \frac{\text{d}y}{\text{d}x} \right|}_{x=-1}} \\
& =\frac{a}{{{\left( 2\left( -1 \right)+3 \right)}^{3}}}-1 \\
& =a-1
\end{aligned}$
Since they are perpendicular to each other,
$\begin{aligned}
{{m}_{\text{tangent}}}\times {{m}_{\text{line}}}&=-1 \\
\left( a-1 \right)\times \frac{1}{5}&=-1 \\
a-1&=-5 \\
a&=-4
\end{aligned}$
Finding the equation of the curve:
$\begin{aligned}
\frac{\text{d}y}{\text{d}x}&=-\frac{4}{{{\left( 2x+3 \right)}^{3}}}-1 \\
y&=\int{-4{{\left( 2x+3 \right)}^{-3}}-1\,\text{d}x} \\
y&=\frac{-4{{\left( 2x+3 \right)}^{-2}}}{\left( -2 \right)\left( 2 \right)}-x+c \\
y&={{\left( 2x+3 \right)}^{-2}}-x+c
\end{aligned}$
Find the value of constant $c$:
When $x=-1,y=0$:
$\begin{aligned}
0&={{\left( -2+3 \right)}^{-2}}-\left( -1 \right)+c \\
0&=1+1+c \\
c&=-2
\end{aligned}$
$\therefore y={{\left( 2x+3 \right)}^{-2}}-x-2$
Equation of curve, $y=\frac{1}{{{\left( 2x+3 \right)}^{2}}}-x-2$
Practice Question 7
Problems involving Partial Fractions
Express $\frac{4-5x}{2+x-{{x}^{2}}}$ in partial fractions. Hence, integrate $\int\limits_{0}^{1}{\frac{4-5x}{2+x-{{x}^{2}}}\,}\text{d}x$.
- I
- II
Factorise the denominator:
$2+x-{{x}^{2}}=\left( 2-x \right)\left( x+1 \right)$
Solve in partial fractions form:
$\begin{aligned}
\frac{4-5x}{\left( 2-x \right)\left( x+1 \right)}&=\frac{A}{2-x}+\frac{B}{x+1} \\
& =\frac{A\left( x+1 \right)+B\left( 2-x \right)}{\left( 2-x \right)\left( x+1 \right)}
\end{aligned}$
$4-5x=A\left( x+1 \right)+B\left( 2-x \right)$
When $x=-1$:
$\begin{aligned}
4-5\left( -1 \right)&=B\left( 2-\left( -1 \right) \right) \\
9&=3B \\
B&=3
\end{aligned}$
When $x=2$:
$\begin{aligned}
4-5\left( 2 \right)&=A\left( 2+1 \right) \\
-6&=A\left( 3 \right) \\
A&=-2
\end{aligned}$
$\therefore \frac{4-5x}{2+x-{{x}^{2}}}=-\frac{2}{2-x}+\frac{3}{x+1}$
Find the integral:
$\begin{aligned}
& \int_{0}^{1}{\frac{4-5x}{2+x-{{x}^{2}}}}\text{ d}x \\
& =\int_{0}^{1}{-\frac{2}{2-x}+\frac{3}{x+1}}\text{ d}x \\
& =\int_{0}^{1}{-2\left( \frac{1}{2-x} \right)+3\left( \frac{1}{x+1} \right)\text{d}x} \\
& =\left[ -2\frac{\ln \left( 2-x \right)}{\left( -1 \right)}+3\ln \left( x+1 \right) \right]_{0}^{1} \\
& =\left[ 2\ln \left( 2-x \right)+3\ln \left( x+1 \right) \right]_{0}^{1} \\
& =\left[ 2\ln \left( 2-1 \right)+3\ln \left( 1+1 \right) \right]-\left[ 2\ln \left( 2-0 \right)+3\ln \left( 0+1 \right) \right] \\
& =2\ln 1+3\ln 2-\left( 2\ln 2+3\ln 1 \right) \\
& =3\ln 2-2\ln 2 \\
& =\ln 2
\end{aligned}$
- I
- II
Factorise the denominator:
$2+x-{{x}^{2}}=\left( 2-x \right)\left( x+1 \right)$
Solve in partial fractions form:
$\begin{aligned}
\frac{4-5x}{\left( 2-x \right)\left( x+1 \right)}&=\frac{A}{2-x}+\frac{B}{x+1} \\
& =\frac{A\left( x+1 \right)+B\left( 2-x \right)}{\left( 2-x \right)\left( x+1 \right)}
\end{aligned}$
$4-5x=A\left( x+1 \right)+B\left( 2-x \right)$
When $x=-1$:
$\begin{aligned}
4-5\left( -1 \right)&=B\left( 2-\left( -1 \right) \right) \\
9&=3B \\
B&=3
\end{aligned}$
When $x=2$:
$\begin{aligned}
4-5\left( 2 \right)&=A\left( 2+1 \right) \\
-6&=A\left( 3 \right) \\
A&=-2
\end{aligned}$
$\therefore \frac{4-5x}{2+x-{{x}^{2}}}=-\frac{2}{2-x}+\frac{3}{x+1}$
Find the integral:
$\begin{aligned}
& \int_{0}^{1}{\frac{4-5x}{2+x-{{x}^{2}}}}\text{ d}x \\
& =\int_{0}^{1}{-\frac{2}{2-x}+\frac{3}{x+1}}\text{ d}x \\
& =\int_{0}^{1}{-2\left( \frac{1}{2-x} \right)+3\left( \frac{1}{x+1} \right)\text{d}x} \\
& =\left[ -2\frac{\ln \left( 2-x \right)}{\left( -1 \right)}+3\ln \left( x+1 \right) \right]_{0}^{1} \\
& =\left[ 2\ln \left( 2-x \right)+3\ln \left( x+1 \right) \right]_{0}^{1} \\
& =\left[ 2\ln \left( 2-1 \right)+3\ln \left( 1+1 \right) \right]-\left[ 2\ln \left( 2-0 \right)+3\ln \left( 0+1 \right) \right] \\
& =2\ln 1+3\ln 2-\left( 2\ln 2+3\ln 1 \right) \\
& =3\ln 2-2\ln 2 \\
& =\ln 2
\end{aligned}$
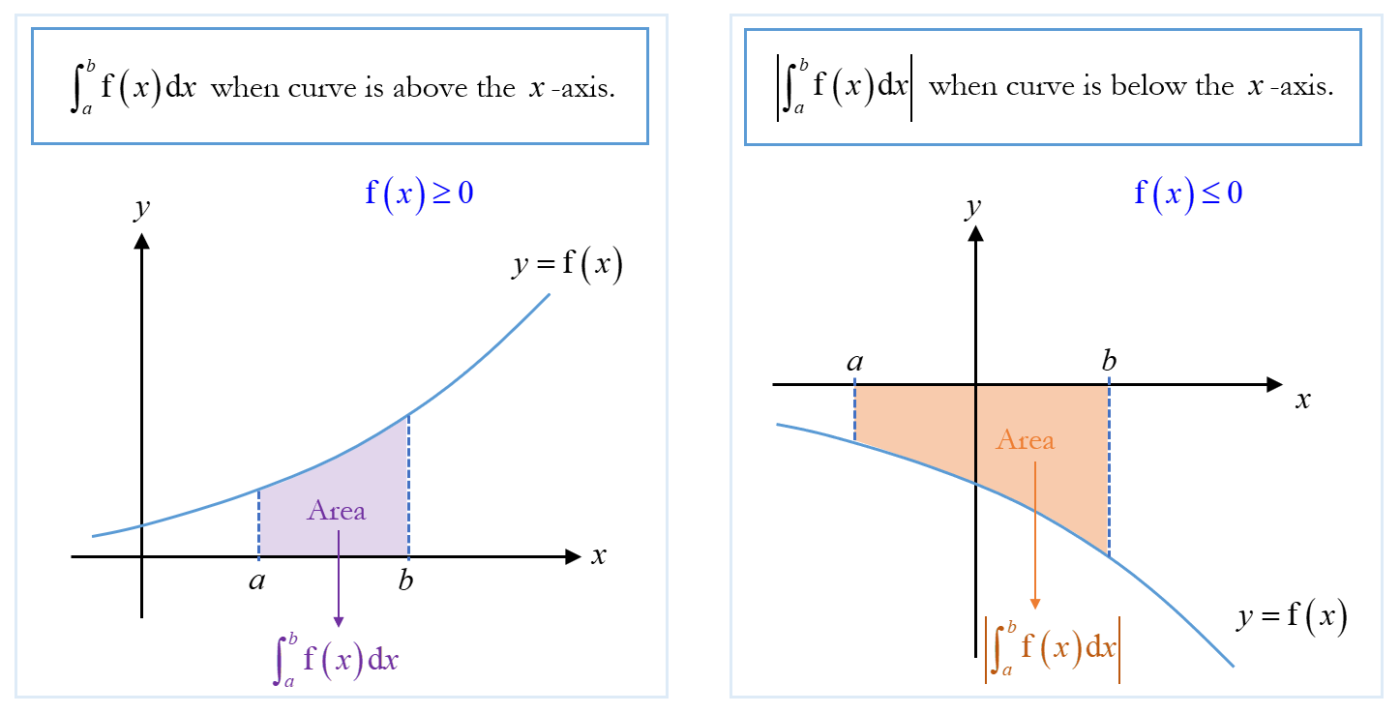
Area Enclosed by the Curve and the $x$-axis
In general, the area enclosed by the curve $y=\text{f}(x)$, the $x$-axis, the lines $x=a$ and $x=b$, where $a<b$, is given by
Practice Question 8
Find the total area enclosed by the curve $y=\left( 3x-2 \right)\left( x+2 \right)$ and the $x$-axis.
$\begin{aligned}
y&=3{{x}^{2}}+6x-2x-4 \\
y&=3{{x}^{2}}+4x-4 \\
\end{aligned}$
- Solution
$\begin{aligned}
\text{Required Area}&=\left| \int_{-2}^{\frac{2}{3}}{y\,\text{d}x} \right| \\
& =\left| \int_{-2}^{\frac{2}{3}}{\left( 3x-2 \right)\left( x+2 \right)\text{d}x} \right| \\
& =\left| \int_{-2}^{\frac{2}{3}}{3{{x}^{2}}+4x-4\,\text{d}x} \right| \\
& =\left| \left[ \frac{3{{x}^{3}}}{3}+\frac{4{{x}^{2}}}{2}-4x \right]_{-2}^{\frac{2}{3}} \right| \\
& =\left| \left( {{x}^{3}}+2{{x}^{2}}-4x \right)_{-2}^{\frac{2}{3}} \right| \\
& =\left| \left[ {{\left( \frac{2}{3} \right)}^{3}}+2{{\left( \frac{2}{3} \right)}^{2}}-4\left( \frac{2}{3} \right) \right]-\left[ {{\left( -2 \right)}^{3}}+2{{\left( -2 \right)}^{2}}-4\left( -2 \right) \right] \right| \\
& =\left| \left( -\frac{40}{27} \right)-\left( 8 \right) \right| \\
& =\left| -9\frac{13}{27} \right| \\
& =9\frac{13}{27}\text{unit}{{\text{s}}^{\text{2}}}
\end{aligned}$
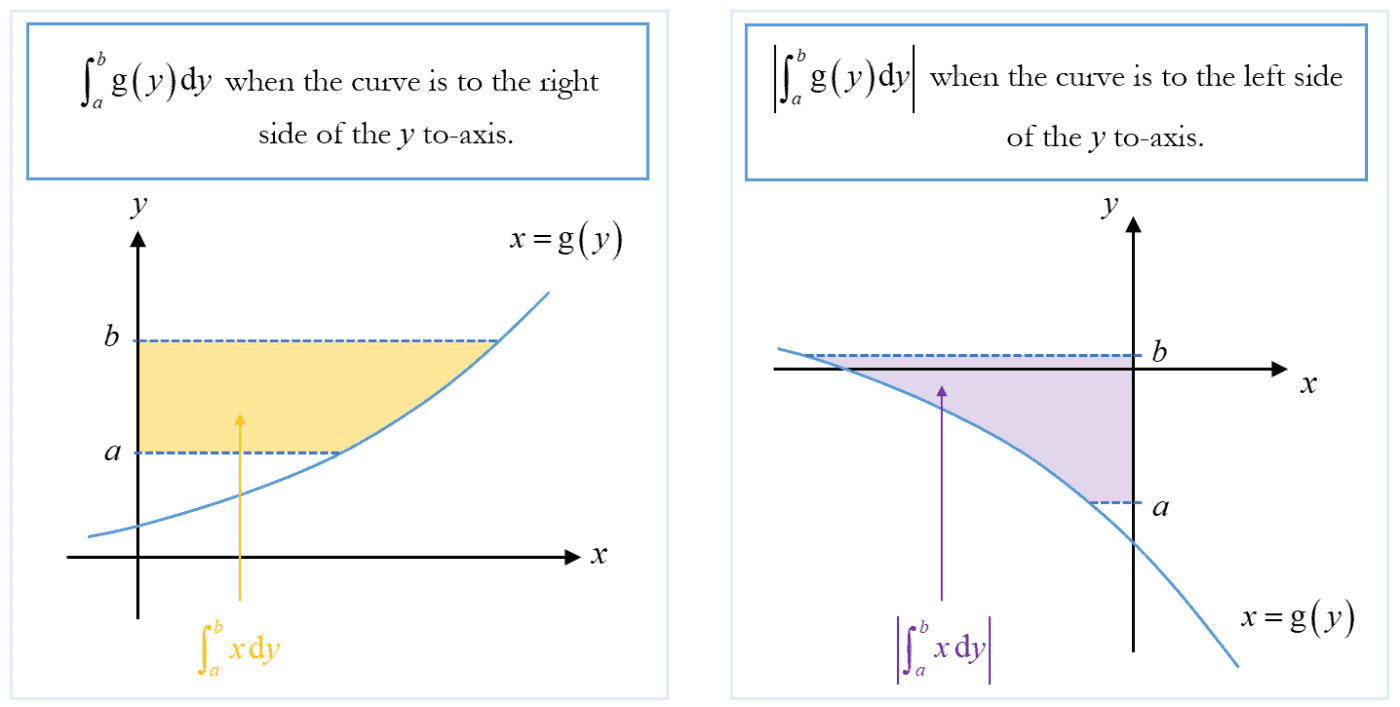
Area Enclosed by the Curve and the $y$-axis
In general, the area enclosed by the curve $x=\text{g}\left( y \right)$, the $y$-axis, the lines $y=a$ and $y=b$, where $a<b$ , is given by
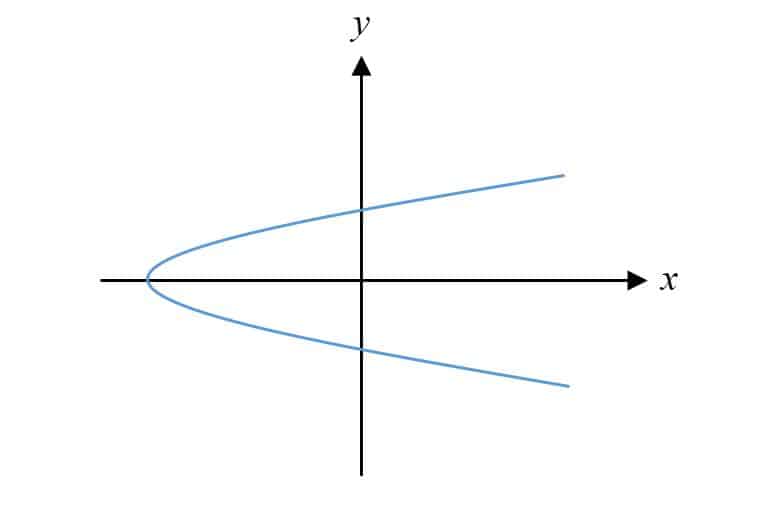
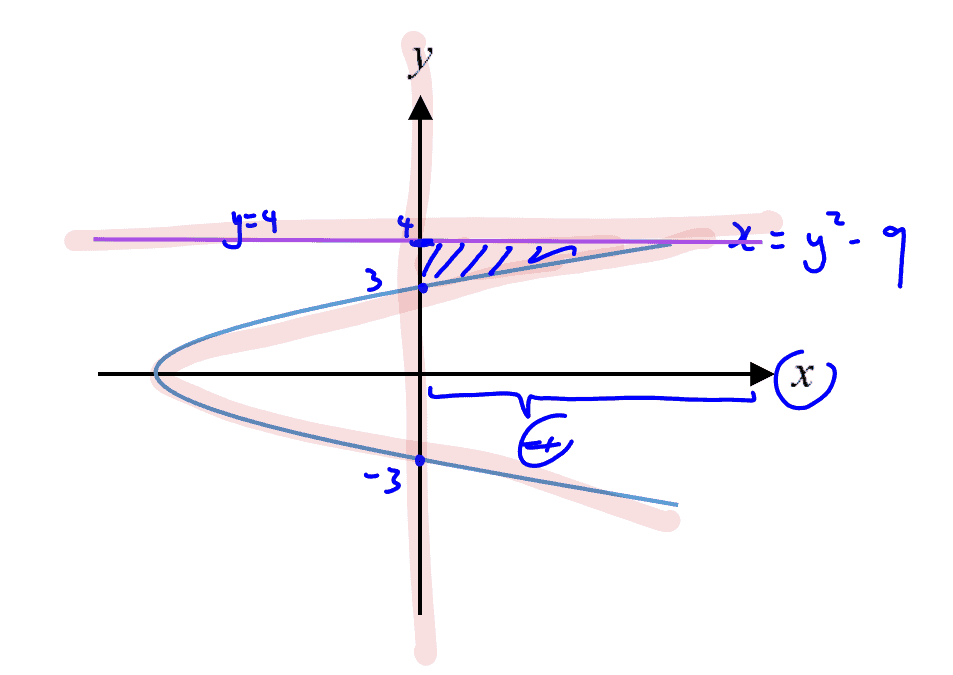
Practice Question 9
The figure shows the curve $x={{y}^{2}}-9$. Find the area of the region bounded by the curve, $y$- axis and the line $y=4$.
- Solution
When $x=0$:
$\begin{aligned}
{{y}^{2}}-9&=0 \\
y&=\pm \sqrt{9} \\
& =3\,\,\text{or}\,\,-3
\end{aligned}$
$\begin{aligned}
\text{Required}\,\text{Area}&=\int_{3}^{4}{x\,\text{d}y} \\
& =\int_{3}^{4}{{{y}^{2}}-9}\,\text{d}y \\
& =\left[ \frac{{{y}^{3}}}{3}-9y \right]_{3}^{4} \\
& =\left( -\frac{44}{3} \right)-\left( -18 \right) \\
& =\frac{10}{3}\text{unit}{{\text{s}}^{2}} \\
& =3\frac{1}{3}\text{unit}{{\text{s}}^{2}}
\end{aligned}$
Area Between Two Curves
Area Enclosed by Curves Projected to the $x$-axis
The area bounded by two curves, $y=\text{f}\left( x \right)$ and $y=\text{g}\left( x \right)$, where $\text{f}\left( x \right)\ge \text{g}\left( x \right)$, from $x=a$ to $x=b$, where $a<b$, is given by $\int\limits_{a}^{b}{\left[ \text{f}\left( x \right)-\text{g}\left( x \right) \right]\text{d}x}$.
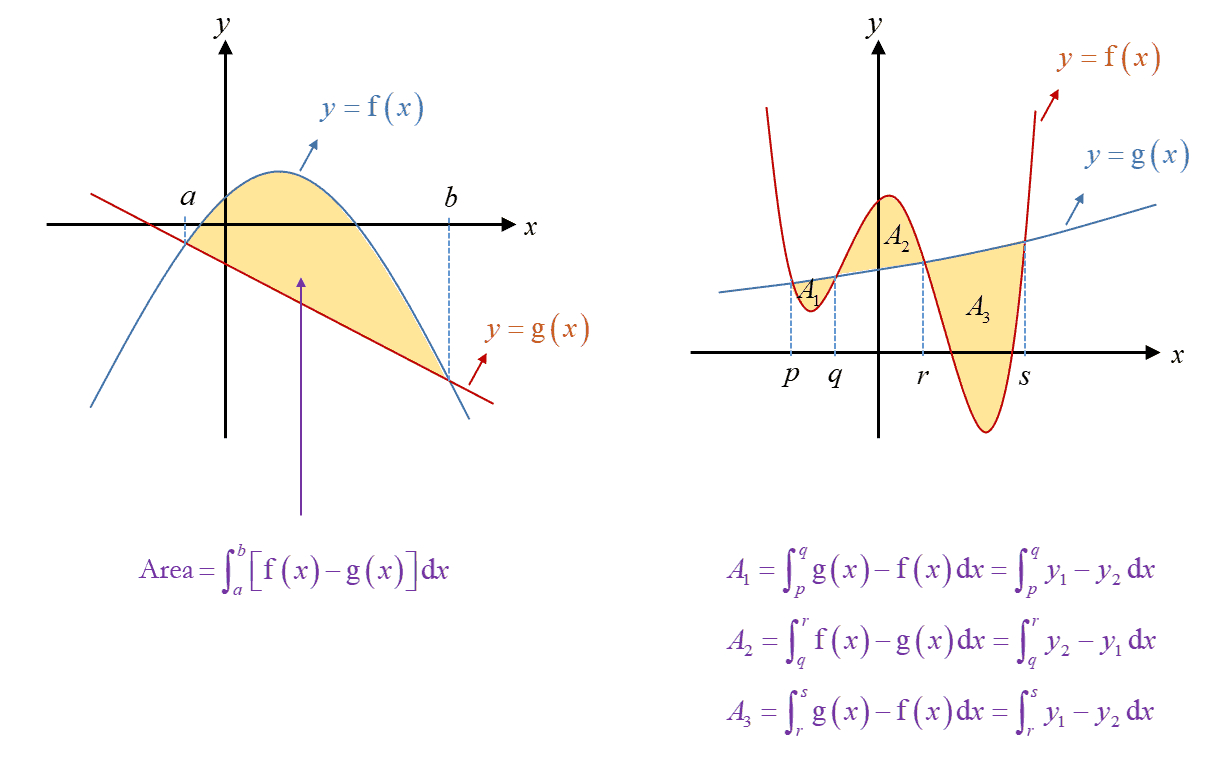
Note: For area between curves, there will not be any negative area generated as we are finding the area between the curves.
Area Enclosed by Curves Projected to the $y$-axis
The area bounded by two curves, $x=\text{f}\left( y \right)$ and $x=\text{g}\left( y \right)$, where $\text{f}\left( y \right)\ge \text{g}\left( y \right)$, from $y=a$ to $y=b$, where $a<b$, is given by $\int\limits_{a}^{b}{\left[ \text{f}\left( y \right)-\text{g}\left( y \right) \right]\text{d}y}$.
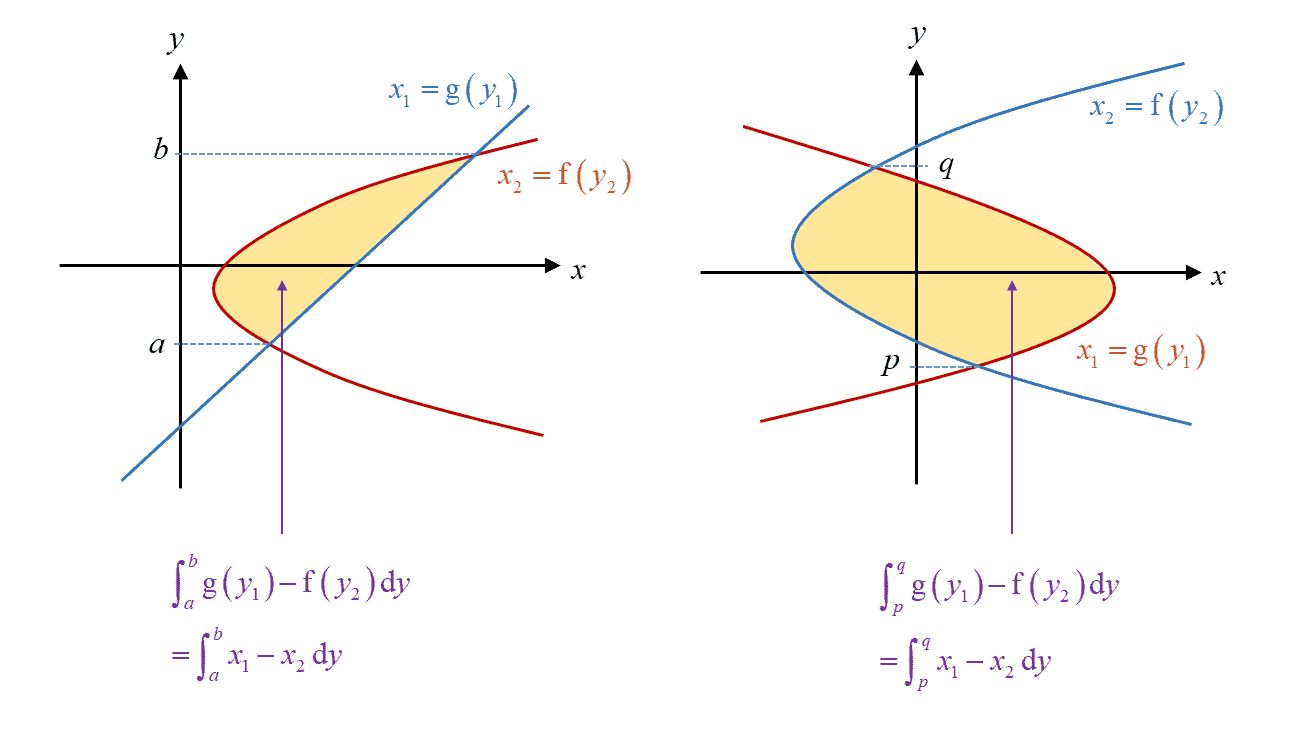
Practice Question 10
The figure shows the two curves $y=-{{x}^{2}}+8x-8$ and $y=-{{\frac{(x-7)}{7}}^{2}}-1$. Find the area of the region bounded by the curves.
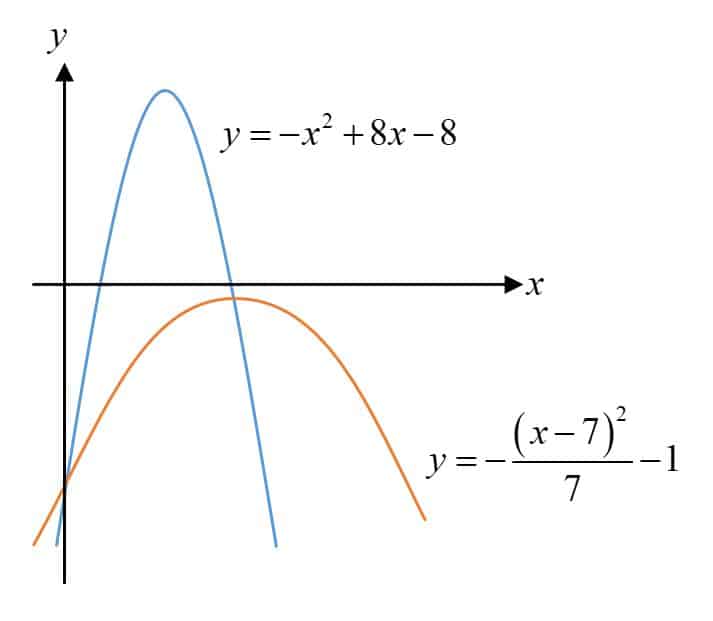
- Solution
To find the intersection point:
$\begin{aligned}
-{{x}^{2}}+8x-8&=-\frac{{{\left( x-7 \right)}^{2}}}{7}-1 \\
-7\left[ {{x}^{2}}+8x-8 \right]&=-7\left[ -\frac{1}{7}{{\left( x-7 \right)}^{2}}-1 \right] \\
7{{x}^{2}}-56x+56&={{\left( x-7 \right)}^{2}}+7 \\
7{{x}^{2}}-56x+56&={{x}^{2}}-14x+49+7 \\
6{{x}^{2}}-42x&=0 \\
6x\left( x-7 \right)&=0 \\
x&=0\,\,\text{or}\,\,7
\end{aligned}$
Required Area
$\begin{aligned}
& =\int_{0}^{7}{\left( -{{x}^{2}}+8x-8 \right)-\left[ -\frac{{{\left( x-7 \right)}^{2}}}{7}-1 \right]}\,\text{d}x \\
& =\int_{0}^{7}{-{{x}^{2}}+8x-8+\frac{1}{7}{{\left( x-7 \right)}^{2}}+1\,\text{d}x} \\
& =\int_{0}^{7}{-{{x}^{2}}+8x+\frac{1}{7}{{\left( x-7 \right)}^{2}}-7\,\text{d}x} \\
& =\left[ -\frac{{{x}^{3}}}{3}+\frac{8{{x}^{2}}}{2}+\frac{1}{7}\cdot \frac{{{\left( x-7 \right)}^{3}}}{3}-7x \right]_{0}^{7} \\
& =\left[ -\frac{1}{3}{{x}^{3}}+4{{x}^{2}}+\frac{1}{21}{{\left( x-7 \right)}^{3}}-7x \right]_{0}^{7} \\
& =\frac{98}{3}-\left( -\frac{49}{3} \right) \\
& =49\,\text{unit}{{\text{s}}^{\text{2}}}
\end{aligned}$
Area under Logarithmic Curve
Practice Question 11
In the diagram, the curve $y=2\ln (x+3)$ cuts the$y$-axis at $(0,q)$. A line, which meets the curve at $(-1,\text{ }p)$ cuts the $y$-axis at $(0,0.5)$.
(a)
State the exact value of $p$ and of $q$.
(a) State the exact value of $p$ and of $q$.
(b)
Calculate the exact area of the shaded region.
(b) Calculate the exact area of the shaded region.
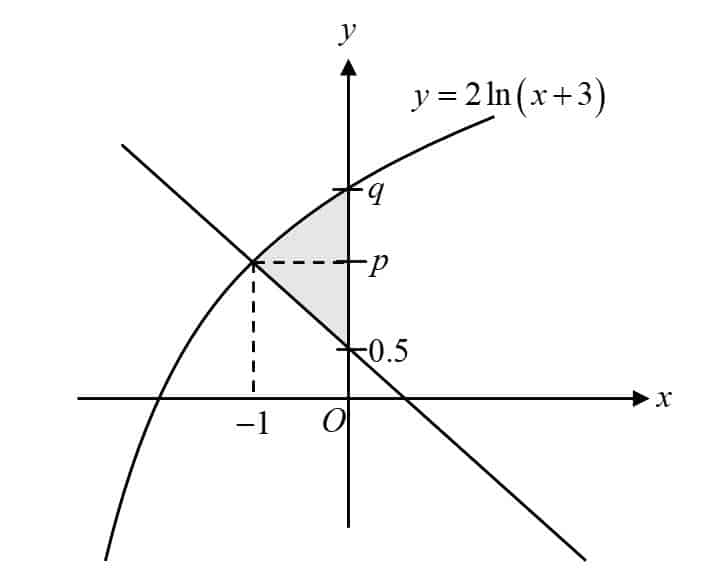
- (a)
- (b)
When $x=0$:
$\begin{aligned}
y&=2\ln \left( 0+3 \right) \\
& =2\ln 3 \\
q&=2\ln 3
\end{aligned}$
When $x=-1$:
$\begin{aligned}
y&=2\ln \left( -1+3 \right) \\
& =2\ln 2 \\
p&=2\ln 2
\end{aligned}$
$q=2\ln 3,p=2\ln 2$
Required Area
$\begin{aligned}
& =\left| \int_{2\ln 2}^{2\ln 3}{{{x}_{1}}}\,\text{d}y \right|+\frac{1}{2}\left( 2\ln 2-\frac{1}{2} \right)\left( 1 \right) \\
& =\left| \int_{2\ln 2}^{2\ln 3}{-3+{{\text{e}}^{\frac{1}{2}y}}}\,\text{d}y \right|+\ln 2-\frac{1}{4} \\
& =\left| \left[ -3y+2{{\text{e}}^{\frac{1}{2}y}} \right]_{2\ln 2}^{2\ln 3} \right|+\ln 2-\frac{1}{4} \\
& =\left[ 3y-2{{\text{e}}^{\frac{1}{2}y}} \right]_{2\ln 2}^{2\ln 3}+\ln 2-\frac{1}{4} \\
& =\left[ 3\left( 2\ln 3 \right)-2{{\text{e}}^{\frac{1}{2}\left( 2\ln 3 \right)}} \right]-\left[ 3\left( 2\ln 2 \right)-2{{\text{e}}^{\frac{1}{2}\left( 2\ln 2 \right)}} \right]+\ln 2-\frac{1}{4} \\
& =6\ln 3-2{{\text{e}}^{\ln 2}}-6\ln 2+2{{\text{e}}^{\ln 2}}+\ln 2-\frac{1}{4} \\
& =6\ln 3-6-5\ln 2+4-\frac{1}{4} \\
& =6\ln 3-5\ln 2-\frac{9}{4}\text{unit}{{\text{s}}^{\text{2}}} \\
\end{aligned}$
Do sign up for our Free Mini-Courses and try our well-structured curriculum to see how it can help to maximize your learning in mathematics online.
Secondary School Additional Mathematics Free Online Course Sign Up.
You may also find the pricing and plans for our Additional Mathematics unlimited all-access courses here!
Topic Lists
Free Mini Course
With our online courses, you can learn at your own pace and take your time whenever it’s most convenient for you. Experience learning with us now for free!
Topics included:
- Derivative as a Gradient Function
- Chain Rule
- Problems involving Tangents and Normals
- Connected Rate of Change Involving Area


