- Home
- Study Guides
Hi students, let’s explore the concept of the Binomial Theorem today! From my experience, this is usually one of the most confusing topics as students approach it with rote memorization instead of seeing the pattern in the expansions.
In this article, I will explain how the formula comes about and provide some examples for you to practice.
Binomial Theorem is a very common topic that can be found in many mathematics syllabi such as the IGCSE Additional Mathematics (0606) and Singapore SEAB Additional Mathematics.
Binomial Theorem - Formula, Expansion and Problems
From previous Elementary Mathematics’ syllabus, we have already learnt the expansion of ${{\left( a+b \right)}^{2}}$.
${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$.
To find ${{\left( a+b \right)}^{3}}$, we will need to multiply ${{\left( a+b \right)}^{2}}$ with $\left( a+b \right)$ and expand the products.
${{\left( a+b \right)}^{3}}={{\left( a+b \right)}^{2}}\left( a+b \right)=\left( {{a}^{2}}+2ab+{{b}^{2}} \right)\left( a+b \right)={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}$.
Similarly for ${{\left( a+b \right)}^{4}}$,
${{\left( a+b \right)}^{4}}={{a}^{4}}+4{{a}^{3}}b+6{{a}^{2}}{{b}^{2}}+4a{{b}^{3}}+{{b}^{4}}$
and so on.
Now, let’s take a look at the three expansions here.
${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$
${{\left( a+b \right)}^{3}}={{a}^{3}}+3{{a}^{2}}b+3a{{b}^{2}}+{{b}^{3}}$
${{\left( a+b \right)}^{4}}={{a}^{4}}+4{{a}^{3}}b+6{{a}^{2}}{{b}^{2}}+4a{{b}^{3}}+{{b}^{4}}$
Did you notice that there is some form of pattern going on with the coefficients when we are trying to expand an expression with two variables?
Basically, this is the essence of the binomial expansion. How do we actually use binomial expansion to expand a given ${{\left( a+b \right)}^{n}}$ formula? This expansion comes in very handy because by using this pattern that revolves around this expansion here, we do not need to painstakingly go through all the different steps in between.
Pascal's Triangle
Before we start, we need to know that there is such a thing called Pascal’s triangle.
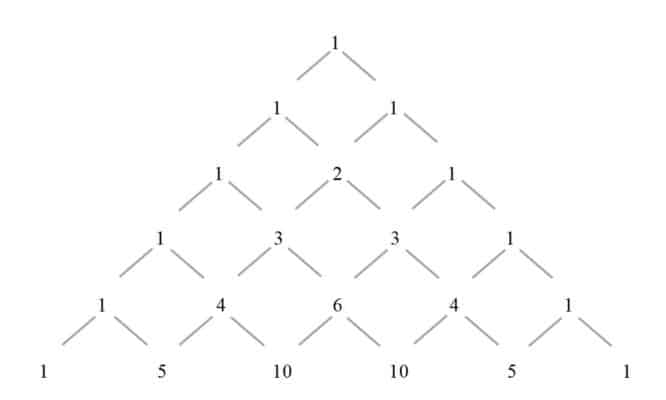
Pascal’s triangle is actually a very fun triangle to play with.
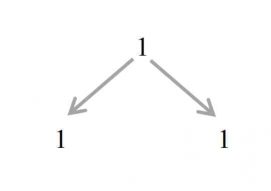
So we start the triangle with one at the top. Then we slide down to both sides and move one in.
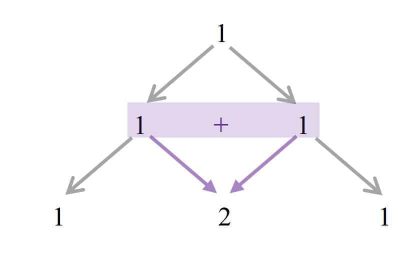
For the interior part, we will have to connect the two numbers above together and add them up.
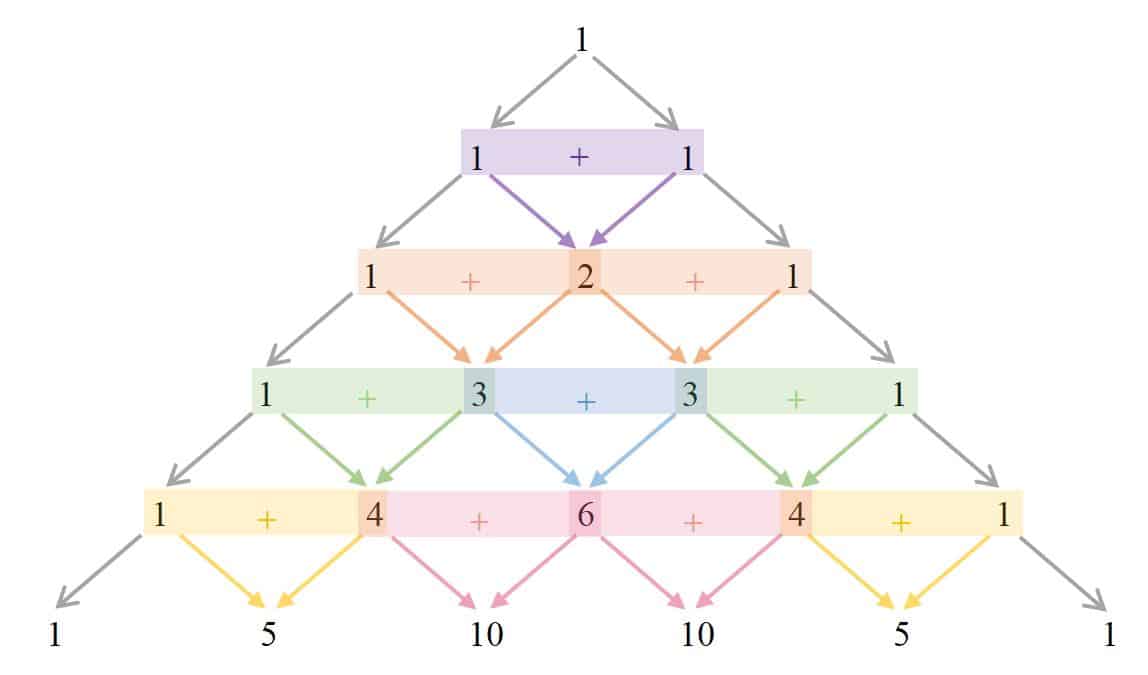
The pattern repeats.
Now, let’s compare the coefficients of the expansions with Pascal’s triangle above.
${{\left( a+b \right)}^{2}}=$$1$${{a}^{2}}+$$2$$ab+$$1$${{b}^{2}}$
${{\left( a+b \right)}^{3}}=$$1$${{a}^{3}}+$$3$${{a}^{2}}b+$$3$$a{{b}^{2}}+$$1$${{b}^{3}}$
${{\left( a+b \right)}^{4}}=$$1$${{a}^{4}}+$$4$${{a}^{3}}b+$$6$${{a}^{2}}{{b}^{2}}+$$4$$a{{b}^{3}}+$$1$${{b}^{4}}$
We could see that there is a similarity in the pattern for the expansion of our expression here. It is pretty obvious how things are working for the coefficients now, but what about the power of the constants? Please note that there is a special pattern of counting for the power of each term in Pascal’s triangle.
${{\left( a+b \right)}^{4}}=1$${{a}^{4}}$${{b}^{0}}$$+4$${{a}^{3}}$${{b}^{1}}$$+6$${{a}^{2}}$${{b}^{2}}$$+4$${{a}^{1}}$${{b}^{3}}$$+1$${{a}^{0}}$${{b}^{4}}$
The powers of the term $a$ descends from $4$ to zero while the powers of the other term, $b$ ascends from zero to $4$.
How Do You Use Pascal's Triangle?
So, if you want to find, for example, ${{\left( a+b \right)}^{5}}$, we could use the subsequent level of Pascal’s triangle to help.
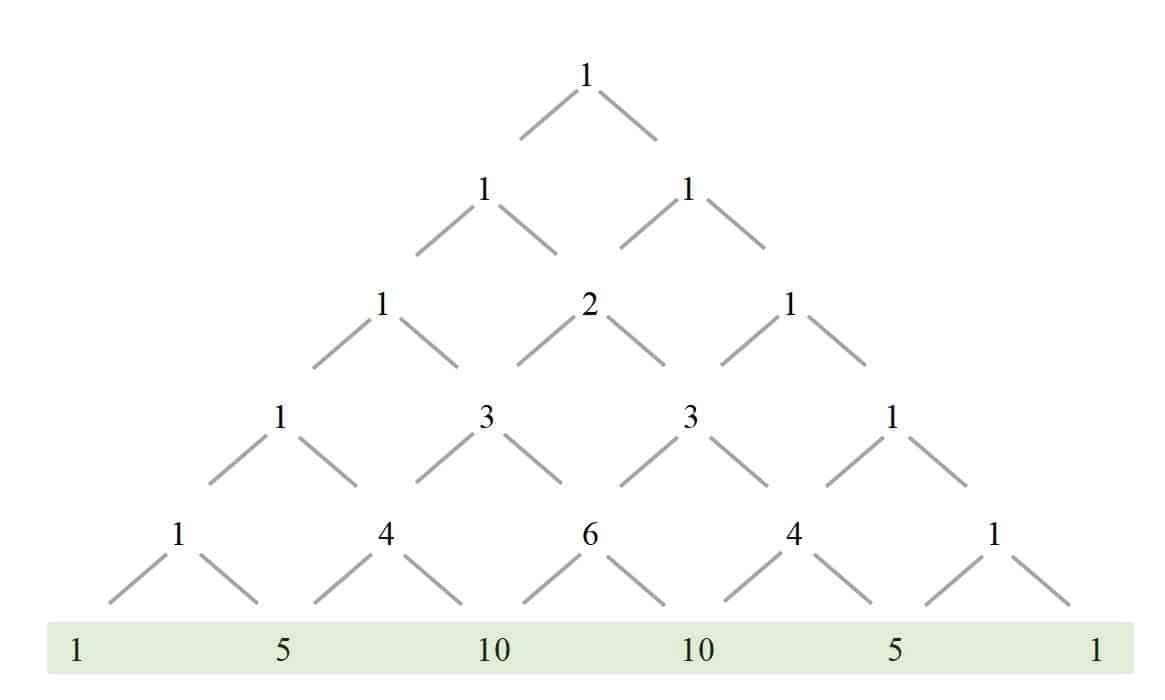
To expand ${{\left( a+b \right)}^{5}}$:
1.
We know that ${{\left(a+b\right)}^{n}}$ would yield $n+1$ terms. So, we could expect to have six terms after the expansion of ${{\left(a+b\right)}^{5}}$.
Let’s write it as:
${{\left( a+b \right)}^{5}}=ab+ab+ab+ab+ab+ab$
2.
Then, run down the powers of the terms where the powers of the term $a$ descend from $5$ to zero while the powers of the other term, $b$ would ascend from zero to $5$.
${{\left( a+b \right)}^{5}}=$${{a}^{5}}$${{b}^{0}}$$+$${{a}^{4}}$${{b}^{1}}$$+$${{a}^{3}}$${{b}^{2}}$$+$${{a}^{2}}$${{b}^{3}}$$+$${{a}^{1}}$${{b}^{4}}$$+$${{a}^{0}}$${{b}^{5}}$
3.
Fill in the coefficients
${{\left( a+b \right)}^{5}}=$$1$${{a}^{5}}{{b}^{0}}+$$5$${{a}^{4}}{{b}^{1}}+$$10$${{a}^{3}}{{b}^{2}}+$$10$${{a}^{2}}{{b}^{3}}+$$5$${{a}^{1}}{{b}^{4}}+$$1$${{a}^{0}}{{b}^{5}}$
4.
Simplify the expansion.
${{\left( a+b \right)}^{5}}={{a}^{5}}+5{{a}^{4}}b+10{{a}^{3}}{{b}^{2}}+10{{a}^{2}}{{b}^{3}}+5a{{b}^{4}}+{{b}^{5}}$
However, it is impossible for us to draw out Pascal’s triangle every time, especially if it involves the expansion of higher powers.
What Is A Binomial Coefficient, And How It Is Calculated?
In fact, there is a formula for us to find the binomial coefficients and this formula is called “$n$ choose $r$” , written as ${}^{n}{{c}_{r}}$ or $\left( \begin{matrix}n \\r \\\end{matrix} \right)$.
But how do we identify the terms in Pascal’s triangle? We need to bear in mind that counting always starts from zero.
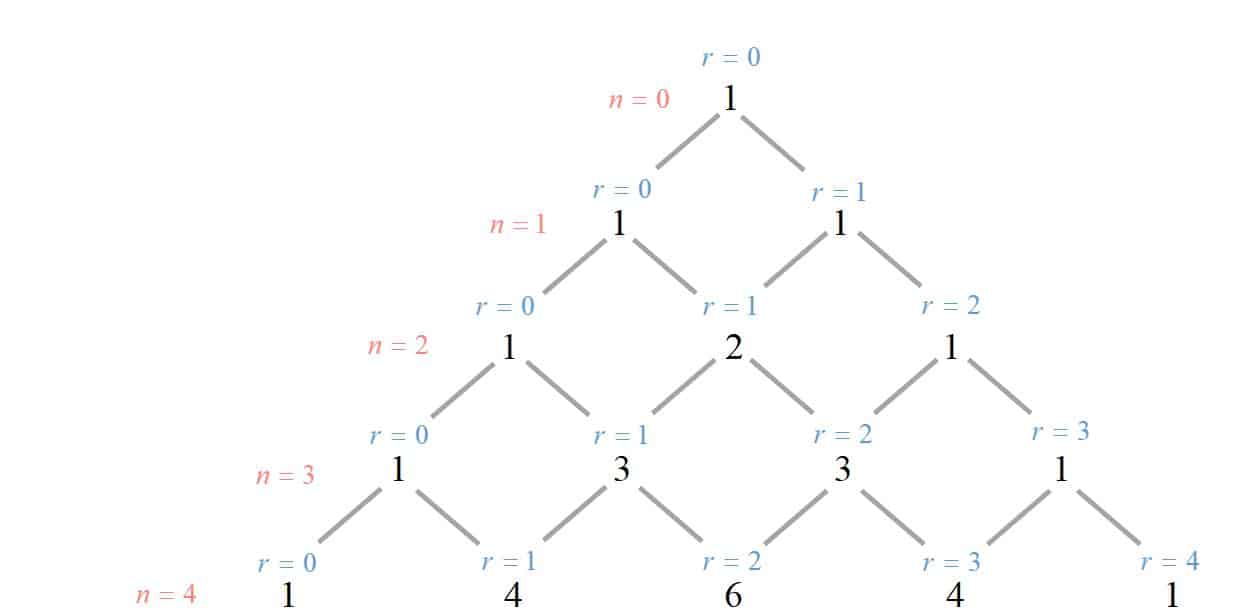
The $n$ refers to the level, which corresponds to the power of the expansion.
This makes it easy to find the coefficient of a particular term as we can use our calculator to find the value of ${}^{n}{{c}_{r}}$.
Example 1
Finding Coefficient of a Specific Term
To find the coefficient of the third term for the expansion ${{\left( a+b \right)}^{5}}$:
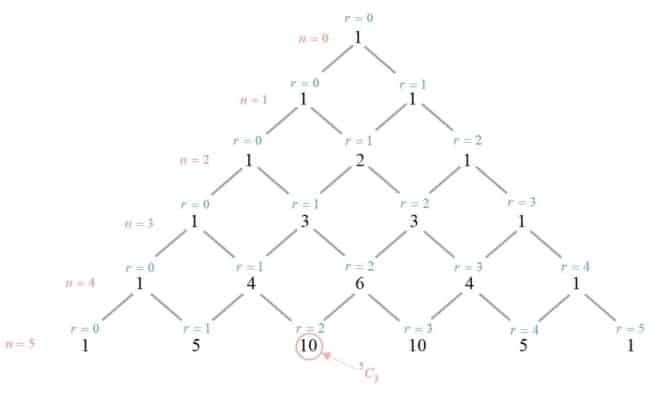 |
$\begin{aligned}{}^{5}{{C}_{3}}&=\left( \begin{matrix}5 \\3 \\\end{matrix} \right) \\ & =\frac{5!}{3!\left( 5-2 \right)!} \\& =10 \end{aligned}$ |
|---|
How To Find The General Term In Binomial Theorem?
For the expansion of ${{(a+b)}^{n}}$ , the general term formula for ${{(r+1)}^{\text{th}}}$ term is ${{T}_{r+1}}=\left( \begin{matrix}n \\r \\\end{matrix} \right){{a}^{(n-r)}}{{b}^{r}}$.
Let’s see how we can apply the general term formula in some simple questions.
(1)
Finding the 5th term of the expansion ${{(1+2x)}^{6}}$
$r=4$ (Note: we start counting from zero hence 5th term will have $r=4$)
5th term, ${{T}_{5}}={{T}_{4+1}}=\left( \begin{matrix}
6 \\
4 \\
\end{matrix} \right){{1}^{(6-4)}}{{\left( 2x \right)}^{4}}=240{{x}^{3}}$
(2)
Finding the 7th term of the expansion ${{(3+x)}^{8}}$
$r=6$ , 7th term, ${{T}_{7}}={{T}_{6+1}}=\left( \begin{matrix}
8 \\
6 \\
\end{matrix} \right){{3}^{(8-6)}}{{\left( x \right)}^{6}}=504{{x}^{3}}$
(3)
Finding the 5th term of the expansion ${{(2x+1)}^{6}}$
$r=4$, 5th term, ${{T}_{5}}={{T}_{4+1}}=\left( \begin{matrix}
6 \\
4 \\
\end{matrix} \right){{\left( 2x \right)}^{(6-4)}}{{\left( 1 \right)}^{4}}=60{{x}^{2}}$
Note that the 5th term of (1) and (3) are different. Why is it different when ${{(1+2x)}^{6}}={{(2x+1)}^{6}}$? It’s because the power of expansion is different. For (1) we ascend the power of $x$ as for (3) we descend the power of $x$. This shows that, though the general term formula is convenient, it’s not all that useful if the context is not given.
This is a brief overview of Pascal’s triangle and Binomial Theorem. Download free printable worksheet here for some extra practice. Now, let’s see how we can solve problems involving binomial theorem in the subsequent questions.
Finding The First Four Terms Of A Binomial Expansion?
Practice Question 1
Binomial Expansion involving Linear Equation
Find, in ascending powers of $x$, the first four terms in the expansion of ${{(2-3x)}^{6}}$.
In the O Level Syllabus, you were given the formula
${{\left( a+b \right)}^{n}}={{a}^{n}}+\left( \begin{matrix}n \\1 \\\end{matrix} \right){{a}^{n-1}}b+\left( \begin{matrix}n \\2 \\\end{matrix} \right){{a}^{n-2}}{{b}^{2}}+…+\left( \begin{matrix}n \\r \\\end{matrix} \right){{a}^{n-r}}{{b}^{r}}+…+{{b}^{n}}$,
where $n$ is a positive integer and $\left( \begin{matrix}n \\r \\\end{matrix} \right)=\frac{n!}{r!\left( n-r \right)!}=\frac{n\left( n-1 \right)…\left( n-r+1 \right)}{r!}$.
To solve this question:
| 1. | From the question, we know that $a=2$, $b=-3x$ and $n=6$. |
|---|---|
| 2. |
Substitute the values into the formula and expand it. $\begin{aligned}{{\left( 2-3x \right)}^{6}}=&\left( \begin{matrix} 6 \\ 0 \\\end{matrix} \right){{\left( 2 \right)}^{6}}{{\left( -3x \right)}^{0}}+\left( \begin{matrix} 6 \\ 1 \\\end{matrix} \right){{\left( 2 \right)}^{5}}{{\left( -3x \right)}^{1}}+\\ &\left( \begin{matrix} 6 \\ 2 \\\end{matrix} \right){{\left( 2 \right)}^{4}}{{\left( -3x \right)}^{2}}+\left( \begin{matrix} 6 \\ 3 \\\end{matrix} \right){{\left( 2 \right)}^{3}}{{\left( -3x \right)}^{3}}+… \\ =&\left( 1 \right){{\left( 2 \right)}^{6}}\left( 1 \right)+6{{\left( 2 \right)}^{5}}\left( -3x \right)+15{{\left( 2 \right)}^{4}}{{\left( -3 \right)}^{2}}{{x}^{2}}\\&+20{{\left( 2 \right)}^{3}}{{\left( -3 \right)}^{3}}{{x}^{3}}+… \\ =&64-576x+2160{{x}^{2}}-4320{{x}^{3}}+… \end{aligned}$ |
Practice Question 2
Binomial Expansion involving Fraction
Find, in ascending powers of $x$, the first four terms in the expansion of ${{\left( 2x+\frac{y}{4} \right)}^{6}}$.
To solve this question:
| 1. | From the question, we know that $a=2x$, $b=\frac{y}{4}$ and $n=6$. |
|---|---|
| 2. |
Substitute the values into the formula and expand it. $\begin{aligned} {{\left( 2x+\frac{y}{4} \right)}^{6}}=&\left( \begin{matrix} 6 \\ 0 \\ \end{matrix} \right){{\left( 2x \right)}^{0}}{{\left( \frac{y}{4} \right)}^{6}}+\left( \begin{matrix} 6 \\ 1 \\ \end{matrix} \right){{\left( 2x \right)}^{1}}{{\left( \frac{y}{4} \right)}^{5}}+\\ &\left( \begin{matrix} 6 \\ 2 \\ \end{matrix} \right){{\left( 2x \right)}^{2}}{{\left( \frac{y}{4} \right)}^{4}}+\left( \begin{matrix} 6 \\ 3 \\ \end{matrix} \right){{\left( 2x \right)}^{3}}{{\left( \frac{y}{4} \right)}^{3}}+… \\ =&\left( 1 \right)\left( 1 \right)\frac{{{y}^{6}}}{{{4}^{6}}}+\frac{6\left( 2 \right)}{{{4}^{5}}}x{{y}^{5}}+\frac{15{{\left( 3 \right)}^{2}}}{{{4}^{4}}}{{x}^{2}}{{y}^{4}}\\ &+\frac{20{{\left( 2 \right)}^{3}}}{{{4}^{3}}}{{x}^{3}}{{y}^{3}}+… \\ =&\frac{1}{4096}{{y}^{6}}+\frac{3}{256}x{{y}^{5}}+\frac{15}{64}{{x}^{2}}{{y}^{4}}+\frac{5}{2}{{x}^{3}}{{y}^{3}}\\&+… \end{aligned}$ |
Finding The Binomial Coefficients?
Practice Question 3
Without the use of a calculator
Evaluate the following without using a calculator.
(a) $\left( \begin{matrix} 10 \\ 3 \\\end{matrix} \right)$,
(b) $\left( \begin{matrix} n+2 \\ 2 \\\end{matrix} \right)$ in terms of $n$,
(c) $\left( \begin{matrix}n+1 \\ n \\\end{matrix} \right)$ in terms of $n$,
(d) $\left( \begin{matrix} n \\n \\\end{matrix} \right)$ in terms of $n$.
- (a)
- (b)
- (c)
- (d)
From the formula, $\left( \begin{matrix}n \\r \\\end{matrix} \right)=\frac{n!}{r!\left( n-r \right)!}=\frac{n\left( n-1 \right)…\left( n-r+1 \right)}{r!}$.
$\begin{aligned}\left( \begin{matrix}n \\ r \\\end{matrix} \right)&=\frac{n!}{r!\left( n-r \right)!} \\\left( \begin{matrix}10 \\ 3 \\\end{matrix} \right)&=\frac{10!}{3!\left( 10-3 \right)!} \\& =\frac{10!}{3!7!} \\& =\frac{10\cdot 9\cdot 8\cdot 7!}{\left( 3\cdot 2\cdot 1 \right)\cdot 7!} \\& =120 \end{aligned}$
$\begin{aligned}\left( \begin{matrix}n+2 \\2 \\\end{matrix} \right)&=\frac{\left( n+2 \right)!}{2!\left( n+2-2 \right)!} \\& =\frac{\left( n+2 \right)!}{2\cdot 1\cdot n!} \\& =\frac{\left( n+2 \right)\left( n+1 \right)n!}{2\cdot n!} \\& =\frac{\left( n+2 \right)\left( n+1 \right)}{2}\end{aligned}$
$\begin{aligned}\left( \begin{matrix}n+1 \\ n\\\end{matrix} \right)&=\frac{\left( n+1 \right)!}{n!\left( n+1-n \right)!} \\& =\frac{\left( n+1 \right)!}{n!1!} \\& =\frac{\left( n+1 \right)n!}{n!} \\& =n+1 \end{aligned}$
$\begin{aligned} \left( \begin{matrix} n \\ n \\\end{matrix} \right)&=\frac{n!}{n!\left( n-n \right)!} \\& =\frac{n!}{n!0!} \\& =1\end{aligned}$
- (a)
- (b)
- (c)
- (d)
From the formula, $\left( \begin{matrix}n \\r \\\end{matrix} \right)=\frac{n!}{r!\left( n-r \right)!}=\frac{n\left( n-1 \right)…\left( n-r+1 \right)}{r!}$.
$\begin{aligned}\left( \begin{matrix}n \\ r \\\end{matrix} \right)&=\frac{n!}{r!\left( n-r \right)!} \\\left( \begin{matrix}10 \\ 3 \\\end{matrix} \right)&=\frac{10!}{3!\left( 10-3 \right)!} \\& =\frac{10!}{3!7!} \\& =\frac{10\cdot 9\cdot 8\cdot 7!}{\left( 3\cdot 2\cdot 1 \right)\cdot 7!} \\& =120 \end{aligned}$
$\begin{aligned}\left( \begin{matrix}n+2 \\2 \\\end{matrix} \right)&=\frac{\left( n+2 \right)!}{2!\left( n+2-2 \right)!} \\& =\frac{\left( n+2 \right)!}{2\cdot 1\cdot n!} \\& =\frac{\left( n+2 \right)\left( n+1 \right)n!}{2\cdot n!} \\& =\frac{\left( n+2 \right)\left( n+1 \right)}{2}\end{aligned}$
$\begin{aligned}\left( \begin{matrix}n+1 \\ n\\\end{matrix} \right)&=\frac{\left( n+1 \right)!}{n!\left( n+1-n \right)!} \\& =\frac{\left( n+1 \right)!}{n!1!} \\& =\frac{\left( n+1 \right)n!}{n!} \\& =n+1 \end{aligned}$
$\begin{aligned} \left( \begin{matrix} n \\ n \\\end{matrix} \right)&=\frac{n!}{n!\left( n-n \right)!} \\& =\frac{n!}{n!0!} \\& =1\end{aligned}$
Practice Question 4
To find the coefficient of a specific term
Find, in ascending powers of $x$, the first three terms in the expansion of ${{\left( 2-\frac{x}{2} \right)}^{6}}.$ Hence, find the coefficient of ${{x}^{2}}$ in the expansion of ${{\left( x+1 \right)}^{2}}{{\left( 2-\frac{x}{2} \right)}^{6}}.$
| 1. | Find the first three terms of ${{\left( 2-\frac{x}{2} \right)}^{6}}$ : $\begin{aligned} {{\left( 2-\frac{x}{2} \right)}^{6}}=&\left( \begin{matrix} 6 \\ 0 \\ \end{matrix} \right){{\left( 2 \right)}^{6}}{{\left( -\frac{x}{2} \right)}^{0}}+\left( \begin{matrix} 6 \\ 1 \\ \end{matrix} \right){{\left( 2 \right)}^{5}}{{\left( -\frac{x}{2} \right)}^{1}}+\\ &\left( \begin{matrix} 6 \\ 2 \\ \end{matrix} \right){{\left( 2 \right)}^{4}}{{\left( -\frac{x}{2} \right)}^{2}}+… \\ =&{{2}^{6}}+6{{\left( 2 \right)}^{5}}\cdot \left( -\frac{1}{2} \right)x+15{{\left( 2 \right)}^{4}}{{\left( -\frac{1}{2} \right)}^{2}}{{\left( x \right)}^{2}}\\&+… \\ =&64-96x+60{{x}^{2}}+… \end{aligned}$ |
|---|---|
| 2. |
Then, multiply ${{\left( x+1 \right)}^{2}}$ to the three terms obtained to Tips: We only need to multiply the terms that would produce ${{x}^{2}}$. $\therefore $coefficient of ${{x}^{2}}=-68$ |
Finding The Unknown Powers For Binomial Expansion?
Practice Question 5
In the expansion of ${{(1-2x)}^{n}}$, where $n$ is a positive integer, in the ascending powers of $x$, the coefficient of the third term is $112$. Find the value of $n$.
| 1. | Expand the term ${{\left( 1-2x \right)}^{n}}$ to find the third term: ${{\left( 1-2x \right)}^{n}}=\left( \begin{matrix} n \\ 0 \\ \end{matrix} \right){{\left( 1 \right)}^{n}}{{\left( -2x \right)}^{0}}+\left( \begin{matrix} n \\ 1 \\ \end{matrix} \right){{\left( 1 \right)}^{n-1}}{{\left( -2x \right)}^{1}}+$$\left( \begin{matrix}n \\2 \\\end{matrix} \right){{\left( 1 \right)}^{n-2}}{{\left( -2x \right)}^{2}}$$+…$ Third term$=\left( \begin{matrix} n \\ 2 \\ \end{matrix} \right){{\left( -2x \right)}^{2}}=\frac{n\left( n-1 \right)}{2!}{{\left( -2 \right)}^{2}}{{x}^{2}}$ |
|---|---|
| 2. |
Compare the coefficient of the third term with $112$
|
Finding A Specific Term of the Expansion?
Practice Question 6
Find the term independent of $x$ in the expansion of ${{\left( {{x}^{3}}-\frac{1}{2x} \right)}^{12}}$.
| 1. | Note that term independent of $x$ refers to the term where the degree of $x=0$, ${{x}^{0}}$. |
|---|---|
| 2. |
Find the general term of ${{\left( {{x}^{3}}-\frac{1}{2x} \right)}^{12}}$. $\begin{aligned} {{\left( {{x}^{3}}-\frac{1}{2x} \right)}^{12}}&=…+\left( \begin{matrix} |
| 3. |
The power of $x$ will be zero since the term is independent of $x$. $\begin{aligned} {{x}^{0}}&={{x}^{36-4r}} \\ |
| 4. |
Substitute $r=9$ into the general term to get the coefficient. $\left( \begin{matrix} 12 \\ |
Solving Binomial Expansion Given The Ratio of Coefficients?
Practice Question 7
Find the value of $n$ in${{(1+2x)}^{n}}$, given that the coefficients of ${{x}^{2}}$ and ${{x}^{3}}$ are in the ratio of $3:14$.
| 1. |
. Write down the general form of ${{\left( 1+2x \right)}^{n}}$. ${{\left( 1+2x \right)}^{n}}=\left( \begin{matrix} |
|---|---|
| 2. |
Find the coefficient of ${{x}^{2}}$; Substitute $r=2$ into the general form. Coefficient of ${{x}^{2}}=\left( \begin{matrix} |
| 3. |
Find the coefficient of ${{x}^{3}}$; Substitute $r=3$ into the general form. Coefficient of ${{x}^{3}}=\left( \begin{matrix} |
| 4. |
Given that the coefficient of ${{x}^{2}}:{{x}^{3}}$ are in the ratio of $3:14$. $\begin{aligned} \frac{\text{coefficient}\,\,\text{of}\,\,{{x}^{2}}}{\text{coefficient}\,\,\text{of}\,\,{{x}^{3}}}&=\frac{3}{14} \\ |
Applications of Binomial Theorem
Practice Question 8
Obtain the first $4$ terms in the expansion, in ascending powers of $x$, of ${{(1-4x)}^{5}}$. Hence, find the value of ${{(0.96)}^{5}}$ correct to $3$ decimal places.
| 1. | Expand the term ${{\left( 1-4x \right)}^{5}}$to find the first four terms: $\begin{aligned} {{\left( 1-4x \right)}^{5}}=&\left( \begin{matrix} 5 \\ 0 \\ \end{matrix} \right){{\left( 1 \right)}^{5}}{{\left( -4x \right)}^{0}}+\left( \begin{matrix} 5 \\ 1 \\ \end{matrix} \right){{\left( 1 \right)}^{4}}{{\left( -4x \right)}^{1}}+\\ &\left( \begin{matrix} 5 \\ 2 \\ \end{matrix} \right){{\left( 1 \right)}^{3}}{{\left( -4x \right)}^{2}}+\left( \begin{matrix} 5 \\ 3 \\ \end{matrix} \right){{\left( 1 \right)}^{2}}{{\left( -4x \right)}^{3}}+… \\ =&1\cdot 1\cdot 1+5\cdot 1\cdot \left( -4x \right)+\\&10\left( 1 \right)\left( 16{{x}^{2}} \right)+10\left( 1 \right)\left( -64 \right){{x}^{3}}+… \\ & =1-20x+160{{x}^{2}}-640{{x}^{3}}+… \end{aligned}$ |
|---|---|
| 2. |
Compare ${{\left( 1-4x \right)}^{5}}$ with ${{\left( 0.96 \right)}^{5}}$: $\begin{aligned} |
| 3. |
Substitute $x=0.01$ into the expansion: $\begin{aligned} |
Special Identities to Remember
- $0!=1$,
- $\left( \begin{matrix}n \\0 \\\end{matrix} \right)=1$,
- $\left( \begin{matrix}n \\1 \\\end{matrix} \right)=n$,
- $\left( \begin{matrix}n \\2 \\\end{matrix} \right)=\frac{n(n-1)}{2!}$,
- $\left( \begin{matrix}n \\3 \\\end{matrix} \right)=\frac{n(n-1)(n-2)}{3!}$,
- $\left( \begin{matrix}n \\n \\\end{matrix} \right)=1$.
Binomial Theorem Formula
Also, remember that this Binomial Theorem Formula is given in the Additional Mathematics Formulae Sheet during GCE O Level Examination
Do sign up for our Free Mini-Courses and try our well-structured curriculum to see how it can help to maximize your learning in mathematics online.
Secondary School Additional Mathematics Free Online Course Sign Up.
You may also find the pricing and plans for our Additional Mathematics unlimited all-access courses here!
Topic List
Free Mini Course
With our online courses, you can learn at your own pace and take your time whenever it’s most convenient for you. Experience learning with us now for free!
Topics included:
- Derivative as a Gradient Function
- Chain Rule
- Problems involving Tangents and Normals
- Connected Rate of Change Involving Area
