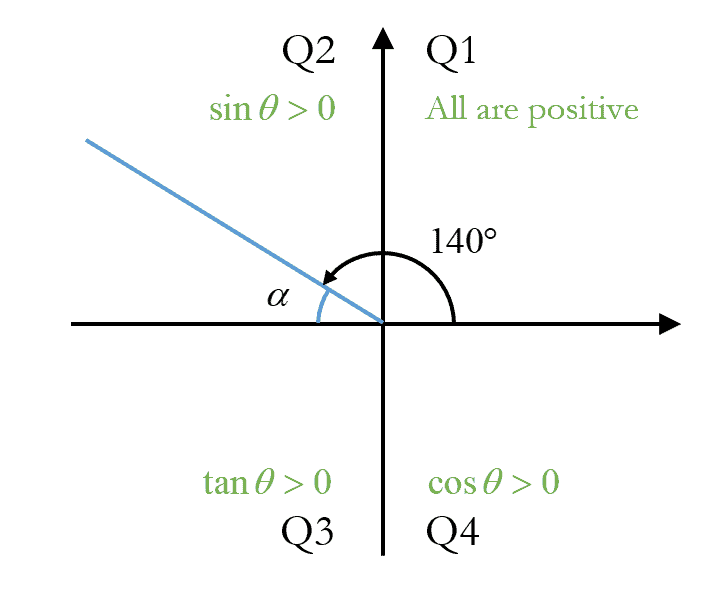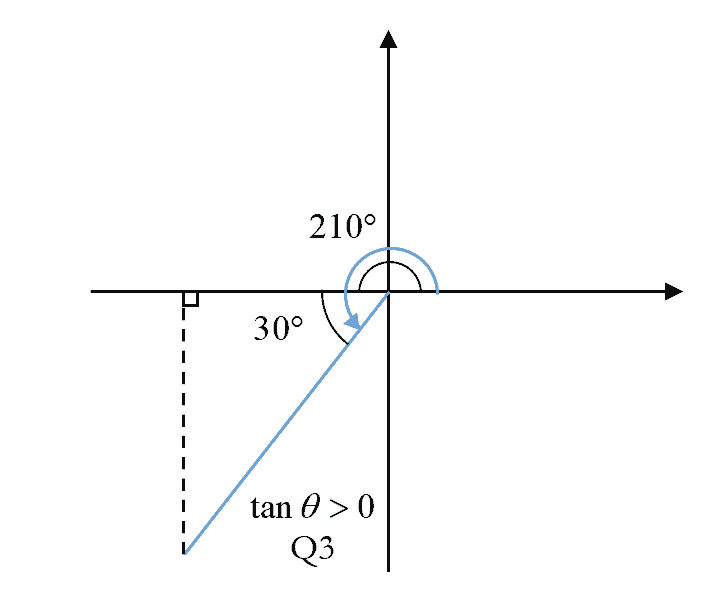O Level | IGCSE | Additional Mathematics

Trigonometric Functions

The Complete Study Guide | Video explanations | Downloadable Worksheets

Many students struggle to master trigonometry, the study of relationships involving right-angled triangles. The six trigonometric functions in relation to a right-angled triangle are used to measure the length of sides and angles of a triangle given its hypotenuse and alternate side or angle.

Sine, cosine, and tangent, the three primary trigonometric functions, are responsible for all other trigonometric functions.

$\sin\theta$

The sine function is the ratio of the opposite side length to that of the hypotenuse.

$\frac{\text{opposite}}{\text{hypotenuse}}$ OR $\frac{1}{\text{cosec }\theta}$

$\cos\theta$

The cosine function is the ratio of the adjacent side length to that of the hypotenuse.

$\frac{\text{adjacent}}{\text{hypotenuse}}$ OR $\frac{1}{\sec\theta}$

$\tan\theta$

The tangent function is the ratio of the opposite side length to the adjacent side length.
This function can also be represented in the form of sine and cosine.

$\frac{\text{opposite}}{\text{adjacent}}$ OR $\frac{\sin\theta}{\cos\theta}$ OR $\frac{1}{\cot\theta}$

The values of trigonometric functions of a general angle cannot be readily calculated unless we are dealing with special angles. Let’s start off with the primary trigonometric functions.

A special angle is an angle where the exact value of one of the trigonometric ratios is known. The trigonometric ratios for the special angles are essential in applications and can be deduced with a little geometry, along with some knowledge of surds.

In this section, we will find the exact values of the special angles. We can use a simple method for doing so, based on the fact that certain basic geometrical shapes have special angles. The special property of the right-angled triangle can also be utilized to find these special angles.

The first shape we have here is an equilateral triangle. An equilateral triangle has three equal-length sides and three angles which are all the same measure, in this case, $60^\circ$.

Since trigonometric ratios have to revolve around a right-angled triangle, we can draw a straight line from the apex of the equilateral triangle to its base to split the triangle into two equal right-angled triangles. This gives us a triangle with angles of $30^\circ$, $60^\circ$ and $90^\circ$.

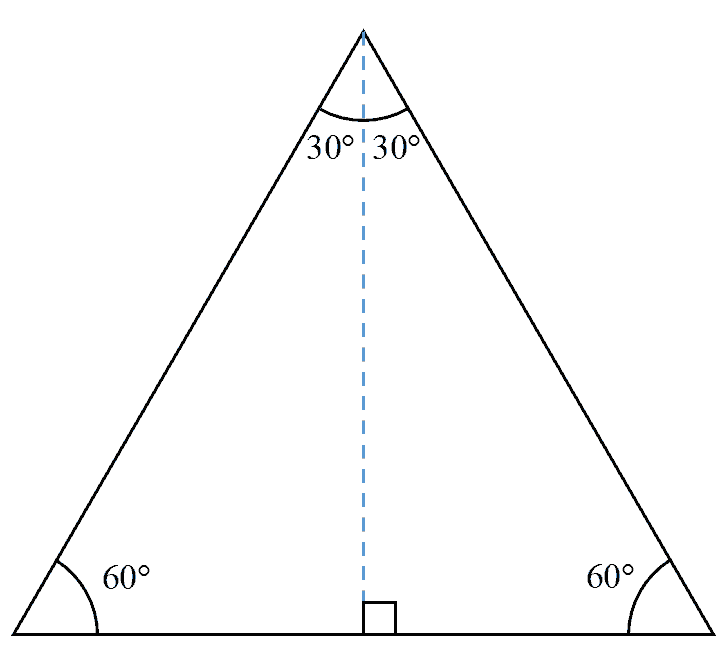
Let the shortest unit of the triangle be $1$ unit. The hypotenuse will be $2$ units as it is twice the length of the shortest unit. To find the height of the triangle, we are going to use Pythagoras’ Theorem.

$\begin{aligned}
c&=\sqrt{{{a}^{2}}+{{b}^{2}}} \\
{{c}^{2}}&={{a}^{2}}+{{b}^{2}} \\
{{2}^{2}}&={{h}^{2}}+{{1}^{2}} \\
{{h}^{2}}&=4-1 \\
h&=\sqrt{3}
\end{aligned}$

$30$ Degrees

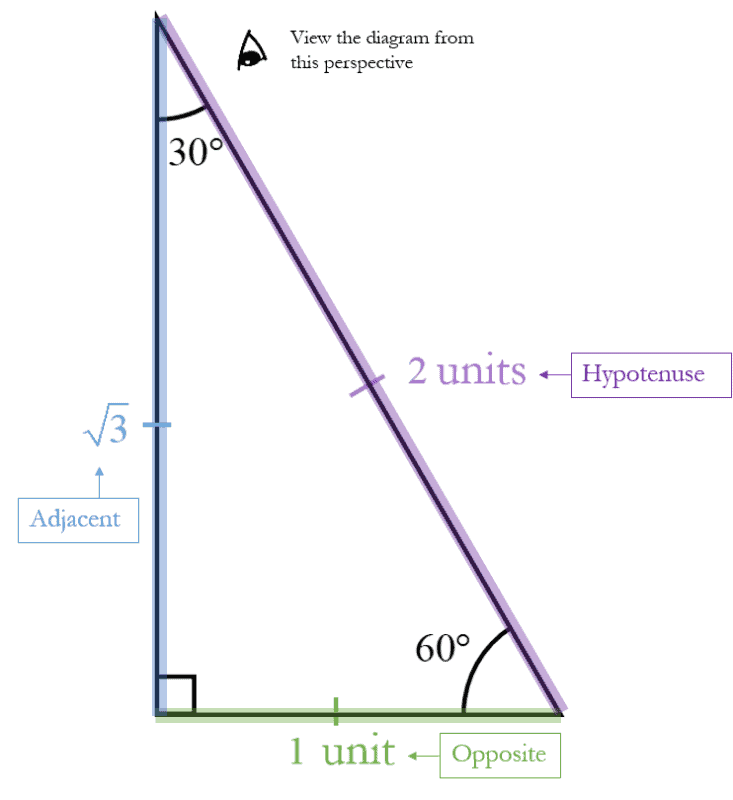
$\theta=30{}^\circ $ or $\frac{\pi }{6}$rad

$\begin{aligned}
\sin \theta &=\frac{\text{opposite}}{\text{hypotenuse}} \\
& =\frac{1}{2}
\end{aligned}$

$\begin{aligned}
\cos \theta &=\frac{\text{adjacent}}{\text{hypotenuse}} \\
& =\frac{\sqrt{3}}{2}
\end{aligned}$

$\begin{aligned}
\tan \theta &=\frac{\text{opposite}}{\text{adjacent}} \\
& =\frac{1}{\sqrt{3}} \\
& =\frac{1}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}} \\
& =\frac{\sqrt{3}}{3}
\end{aligned}$

$60$ Degrees

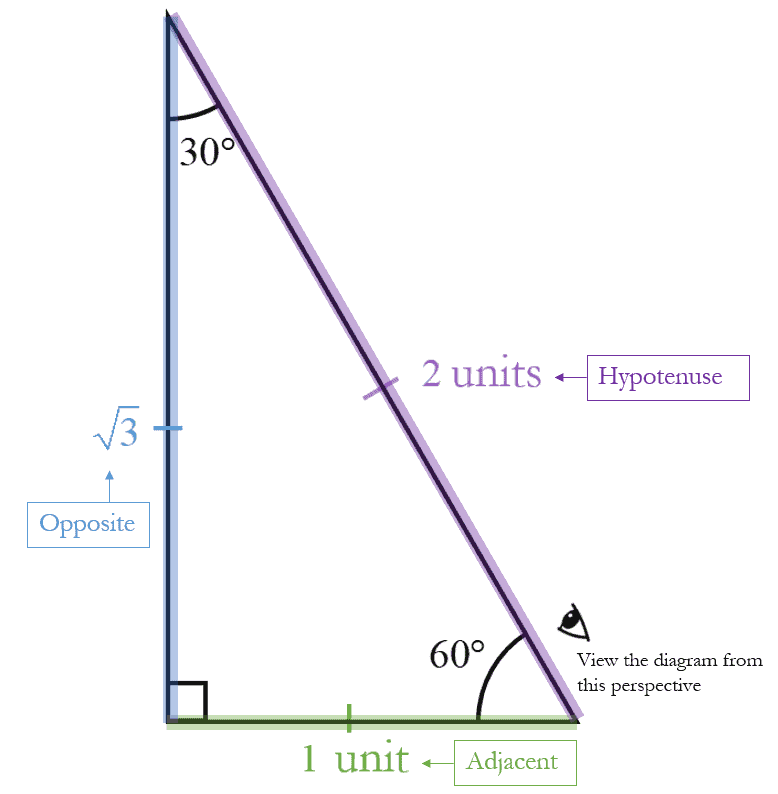
$\theta=60{}^\circ $ or $\frac{\pi }{3}$rad

$\begin{aligned}
\sin \theta &=\frac{\text{opposite}}{\text{hypotenuse}} \\
& =\frac{\sqrt{3}}{2}
\end{aligned}$

$\begin{aligned}
\cos \theta &=\frac{\text{adjacent}}{\text{hypotenuse}} \\
& =\frac{1}{2}
\end{aligned}$

$\begin{aligned}
\tan \theta &=\frac{\text{opposite}}{\text{adjacent}} \\
& =\frac{\sqrt{3}}{1} \\
& =\sqrt{3}
\end{aligned}$

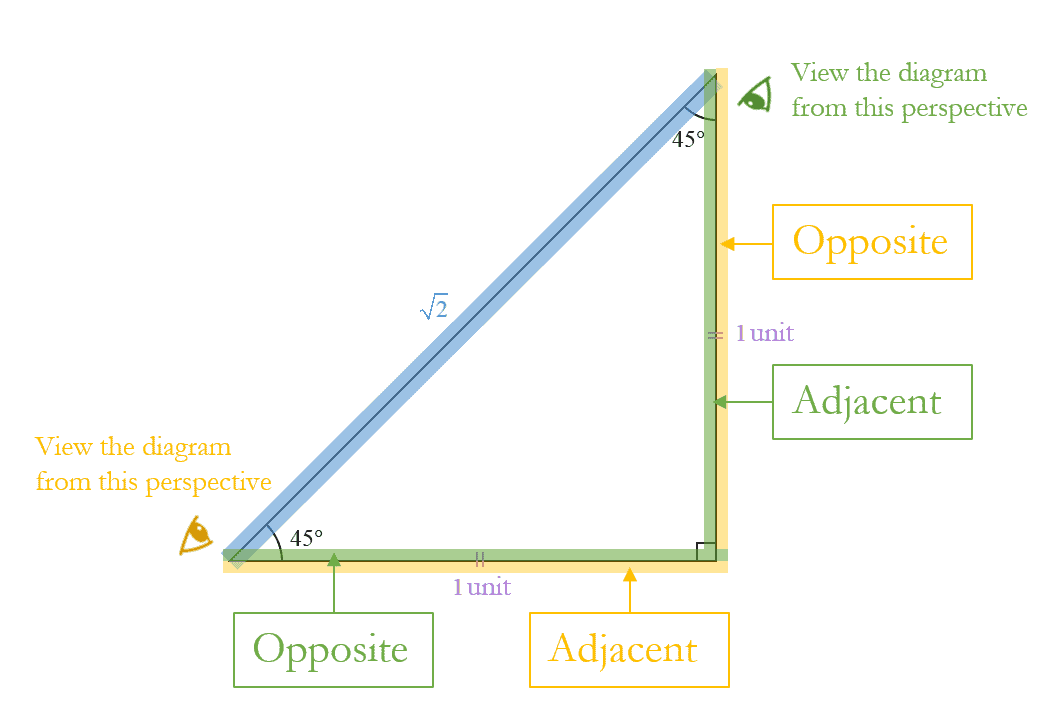
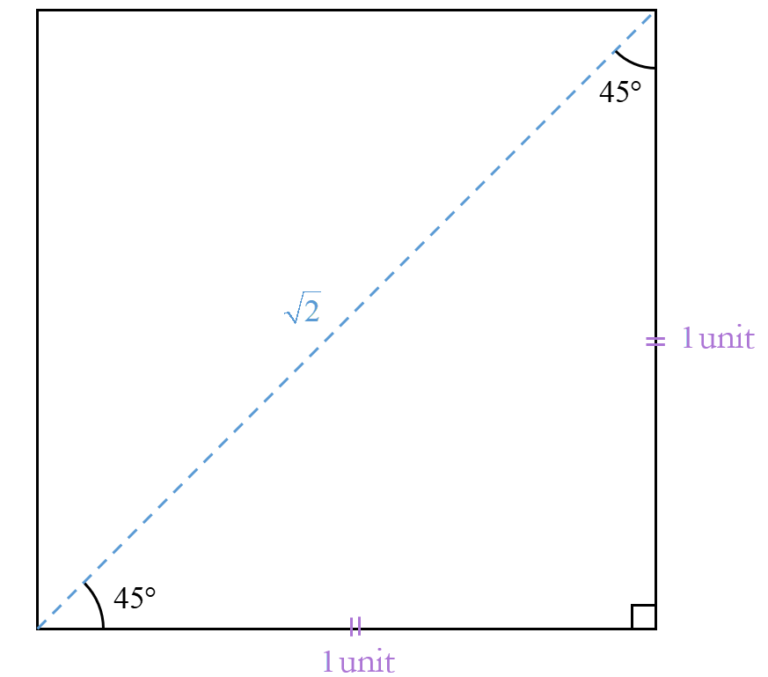
Next is an isosceles triangle, a triangle in which at least two of the sides are congruent (equal in length).

We can draw a diagonal line from corner to corner of the square, as shown at left. Then we see that the square is split into two congruent right-angled triangles. This gives us a triangle with angles of $45^\circ$ and $90^\circ$.

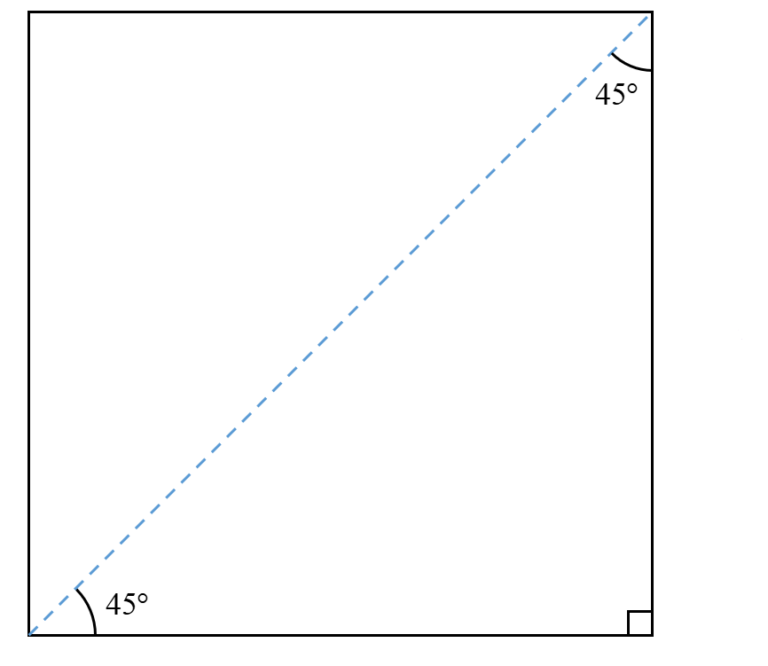
The original square has sides of length $1$ unit. Since this is an isosceles triangle, we can use the Pythagoras’ Theorem to find the hypotenuse.

$\begin{aligned}
c&=\sqrt{{{a}^{2}}+{{b}^{2}}} \\
& =\sqrt{{{1}^{2}}+{{1}^{2}}} \\
& =\sqrt{2}
\end{aligned}$

$45$ Degrees

Click image to view in full size

$\theta=45{}^\circ $ or $\frac{\pi }{4}$rad

$\begin{aligned}
\sin \theta &=\frac{\text{opposite}}{\text{hypotenuse}} \\
& =\frac{1}{\sqrt{2}}
\end{aligned}$

$\begin{aligned}
\cos \theta &=\frac{\text{adjacent}}{\text{hypotenuse}} \\
& =\frac{1}{\sqrt{2}}
\end{aligned}$

$\begin{aligned}
\tan \theta &=\frac{\text{opposite}}{\text{adjacent}} \\
& =\frac{1}{1} \\
& =1
\end{aligned}$

Trigonometric Values of Special Angle

$\theta $	$30{}^\circ $ or $\frac{\pi }{6}$rad	$45{}^\circ $ or $\frac{\pi }{4}$rad	$60{}^\circ $ or $\frac{\pi }{3}$rad
$\sin \theta $	$\frac{1}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{\sqrt{3}}{2}$
$\cos \theta $	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{2}$
$\tan \theta $	$\frac{1}{\sqrt{3}}=\frac{\sqrt{3}}{3}$	$1$	$\frac{\sqrt{3}}{1}=\sqrt{3}$

Practice Question 1

Without using a calculator, find the exact value of $\frac{\sin \frac{\pi }{4}}{\cos \frac{\pi }{3}}$.

Solution

$\begin{aligned}
\frac{\sin \frac{\pi }{4}}{\cos \frac{\pi }{3}}&=\frac{\frac{1}{\sqrt{2}}}{\frac{1}{2}} \\
& =\frac{1}{\sqrt{2}}\times \frac{2}{1} \\
& =\frac{2}{\sqrt{2}} \\
& =\frac{2}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}} \\
& =\sqrt{2}
\end{aligned}$

Clockwise and Anticlockwise Rotations

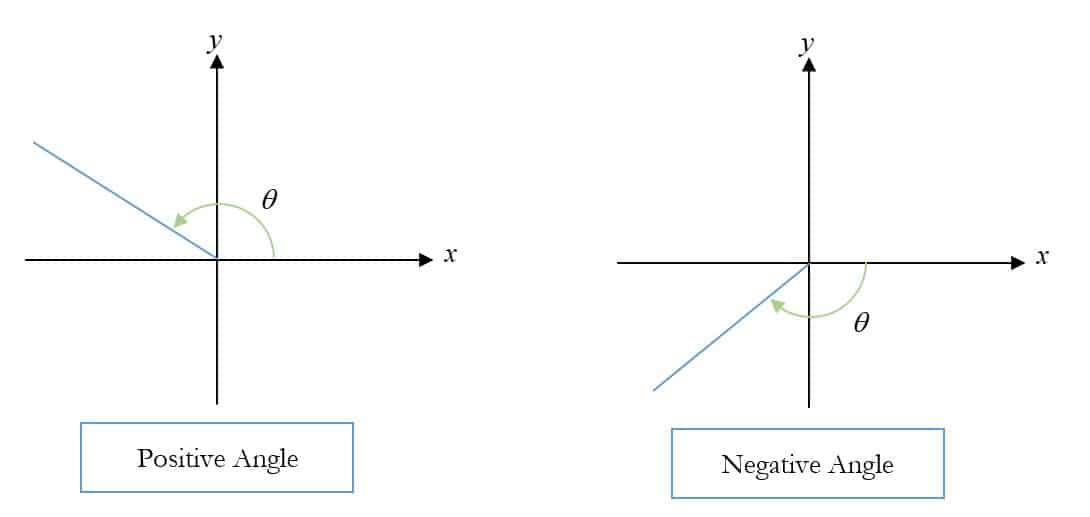
We have all seen objects rotate or revolve, and we know that they can do so in two different ways. The direction in which a plane deviates from a line is called an angle. It can be positive or negative. We know that the hands of a clock go in a clockwise direction but in trigonometry, angles are always measured in the anticlockwise direction from the positive $x$-axis.

The angle measured in an anticlockwise direction has a positive value.

The angle measured in a clockwise direction has a negative value.

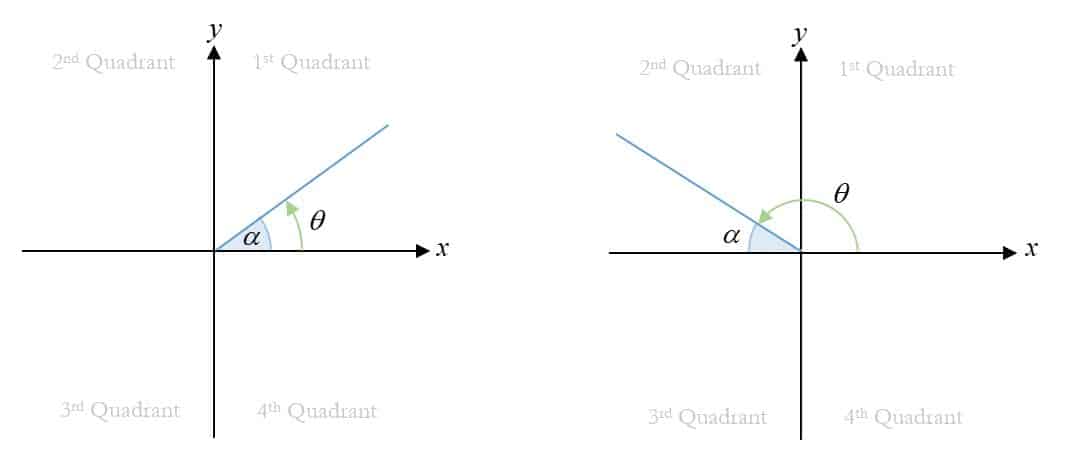
Basic Angle, $\alpha$

The basic acute angle or the reference angle, $\alpha$, is the acute angle that the given angle makes with the $x$-axis.

Left figure: $\left( \theta =\alpha \right)$

Right figure: $\left(\theta =180{}^\circ -\alpha^\circ \right)$ OR $\left(\theta =\pi -\alpha \right)$

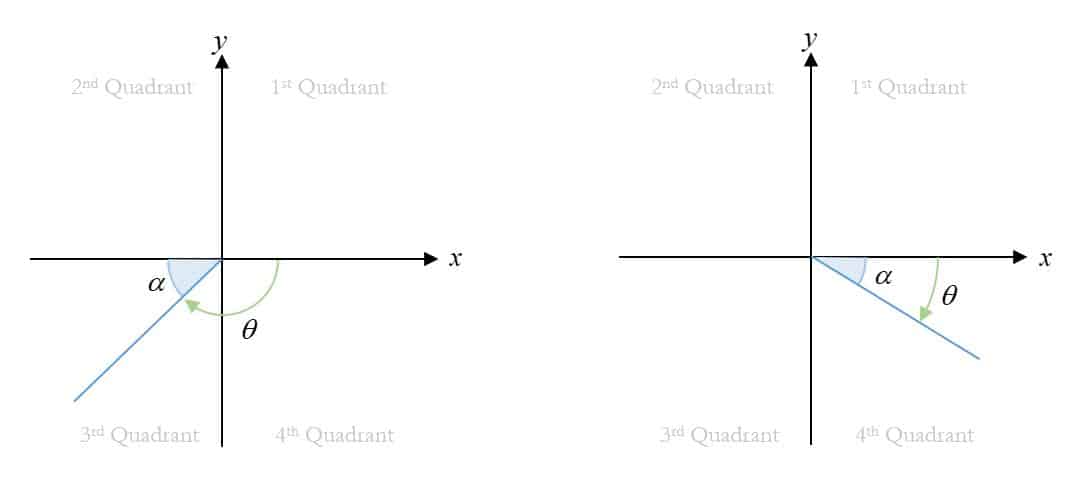
Left figure: $\left(\theta =180{}^\circ +\alpha^\circ \right)$ OR $\left(\theta =\pi +\alpha \right)$

Right figure: $\left(\theta =360{}^\circ -\alpha^\circ \right)$ OR $\left(\theta =2\pi -\alpha \right)$

Practice Question 2

Express $\sin \theta$, $\cos \theta$ and $\tan \theta$ in terms of the ratios of its basic angles when $\theta=140^\circ $.

Solution
Image

Basic angle, $\alpha =180{}^\circ -140{}^\circ =40{}^\circ $

$\begin{aligned}
\sin 140{}^\circ &=40{}^\circ \\
\cos 140{}^\circ &=-\cos 40{}^\circ \\
\tan 140{}^\circ &=-\tan 40{}^\circ
\end{aligned}$

ASTC Rules

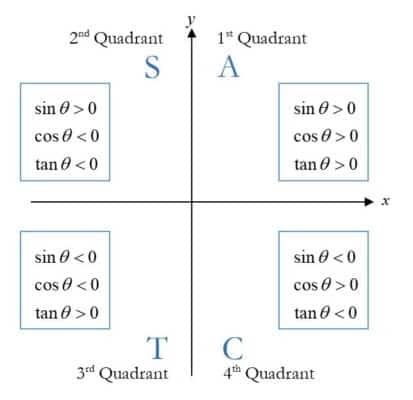
We can easily solve trigonometric questions by identifying the $4$ quadrants and calculating the angles in degrees or radians. The four quadrants of the coordinate plane are important for trigonometric calculations, and it’s helpful to have a quick visual reference for angles. The four quadrants of the coordinate plane are numbered anticlockwise as shown in the figure.

The easiest way to remember is by using the mnemonic ASTC – All Students Take Calculus.

1st Quadrant
2nd Quadrant
3rd Quadrant
4th Quadrant

If a given angle is in the first quadrant ($0^\circ$ to $90^\circ$), then all trigonometric ratios in that angle will be positive.

The letter ‘A’ in ASTC indicates that all trigonometric ratios in the first quadrant are positive.

If a given angle is in the second quadrant ($90^\circ$ to $180^\circ$), then all trigonometric ratios in that angle will be negative except for sine.

The letter ‘S’ in ASTC indicates that only sine in the second quadrant is positive.

If a given angle is in the third quadrant ($180^\circ$ to $270^\circ$), then all trigonometric ratios in that angle will be negative except for tangent.

The letter ‘T’ in ASTC indicates that only the tangent in the third quadrant is positive.

If a given angle is in the fourth quadrant ($270^\circ$ to $360^\circ$), then all trigonometric ratios in that angle will be negative except for cosine.

The letter ‘C’ in ASTC indicates that only cosine in the fourth quadrant is positive.

Any time you are given an angle measurement in degrees, you can use this ASTC rule to figure out which quadrant your ratio will be in. We know that trigonometric ratios can be expressed in both positive and negative forms, but only one of those forms is true for any given angle.

1st Quadrant
2nd Quadrant
3rd Quadrant
4th Quadrant

First Quadrant:
$\left( \theta =\alpha \right)$

$\begin{aligned}
\sin \theta &=\sin \alpha \\
\cos \theta &=\cos \alpha \\
\tan \theta &=\tan \alpha
\end{aligned}$

Second Quadrant: $\left(\theta =180{}^\circ -\alpha^\circ \right)$ OR $\left(\theta =\pi -\alpha \right)$

$\begin{aligned}
\sin \theta &=\sin \alpha \\
\cos \theta &=-\cos \alpha \\
\tan \theta &=-\tan \alpha
\end{aligned}$

Third Quadrant: $\left(\theta =180{}^\circ +\alpha^\circ \right)$ OR $\left(\theta =\pi +\alpha \right)$

$\begin{aligned}
\sin \theta &=-\sin \alpha \\
\cos \theta &=-\cos \alpha \\
\tan \theta &=\tan \alpha
\end{aligned}$

Fourth Quadrant: $\left(\theta =360{}^\circ -\alpha^\circ \right)$ OR $\left(\theta =2\pi -\alpha \right)$

$\begin{aligned}
\sin \theta &=-\sin \alpha \\
\cos \theta &=\cos \alpha \\
\tan \theta &=-\tan \alpha
\end{aligned}$

Practice Question 3

Find the exact value of each of the following.

(a)

$\tan 210^\circ$

(a) $\tan 210^\circ$

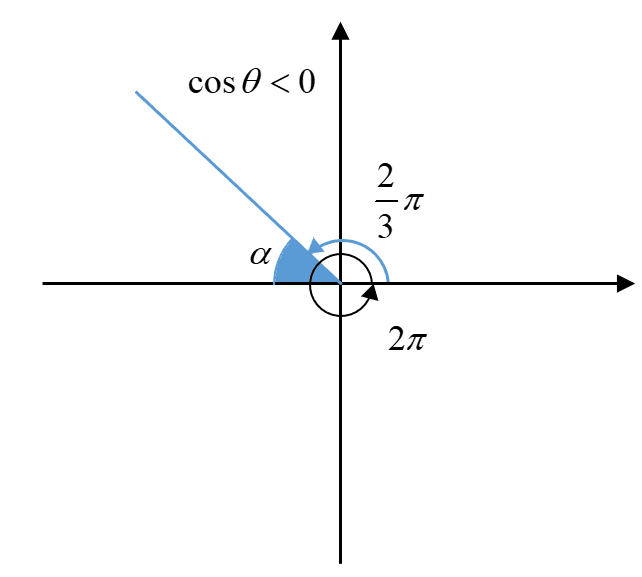
(b)

$\cos \frac{8}{3}\pi $

(b) $\cos \frac{8}{3}\pi $

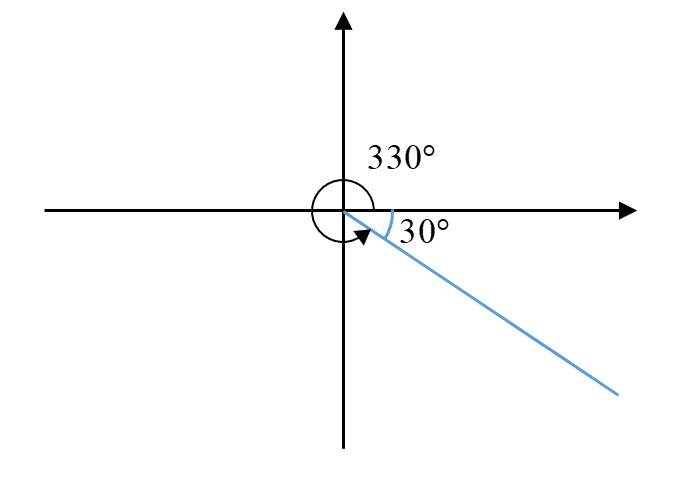
(c)

$\sin 330^\circ$

Solution
Image

Basic angle, $\alpha =30{}^\circ $

$\begin{aligned}
\tan 210{}^\circ &=\tan 30{}^\circ \\
& =\frac{1}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}} \\
& =\frac{\sqrt{3}}{3}
\end{aligned}$

Solution
Image

Basic angle,
$\begin{aligned}
\alpha &=\pi -\frac{2}{3}\pi \\
& =\frac{1}{3}\pi
\end{aligned}$

$\begin{aligned}
\cos \left( \frac{8}{3}\pi \right)&=-\cos \left( \frac{1}{3}\pi \right) \\
& =-\frac{1}{2}
\end{aligned}$

Solution
Image

Basic angle, $\alpha =30{}^\circ$

$\begin{aligned}\sin 330{}^\circ&=-\sin \left( 30{}^\circ\right) \\& =-\frac{1}{2}\end{aligned}$

The other trigonometric functions such as cotangent, secant, and cosecant can be derived from the primary trigonometric functions. The reciprocal of sine is cosecant, the reciprocal of cosine is secant, and the reciprocal of tangent is cotangent. All these ratios are reciprocals of each other.

$\cot\theta$

The cotangent function is the ratio of the adjacent side length to the opposite side length.

$\frac{1}{\tan\theta}$ OR $\frac{\text{adjacent}}{\text{opposite}}$.

$\sec\theta$

The secant function is the ratio of the hypothenuse to the adjacent side length.

$\frac{1}{\cos\theta}$ OR $\frac{\text{hypotenuse}}{\text{adjacent}}$

$\text{cosec }\theta$

The cosecant function is the ratio of the hypothenuse to the opposite side length.

$\frac{1}{\sin\theta}$ OR $\frac{\text{hypotenuse}}{\text{opposite}}$

Tip: Look at the third letter to determine the reciprocal of the trigonometric ratio.

Please note that:

${{\cos }^{n}}\theta ={{\left( \cos \theta \right)}^{n}},{{\sin }^{n}}\theta ={{\left( \sin \theta \right)}^{n}},{{\tan }^{n}}\theta ={{\left( \tan \theta \right)}^{n}}$ for $n\ge 1$,

Example 1
Example 2
Example 3

${{\cos}^{2}}\theta ={{\left( \cos\theta \right)}^{2}}$

${{\sin}^{3}}\theta ={{\left( \sin\theta \right)}^{3}}$

${{\tan}^{5}}\theta ={{\left( \tan \theta \right)}^{5}}$

BUT

${{\cos }^{-1}}\theta \ne {{\left( \cos \theta \right)}^{-1}},{{\sin }^{-1}}\theta \ne {{\left( \sin \theta \right)}^{-1}}$ and ${{\tan }^{-1}}\theta ={{\left( \tan \theta \right)}^{-1}}$

Example 1
Example 2
Example 3

$y={{\cos }^{-1}}x\Leftrightarrow \cos y=x$

$y={{\sin }^{-1}}x\Leftrightarrow \sin y=x$

$y={{\tan }^{-1}}x\Leftrightarrow \tan y=x$

Practice Question 4

Given that $\cos \theta=\frac{2}{7}$ and $\theta$ is acute, without using a calculator, find

(i)

$\sec \theta$,

(i) $\sec \theta$,

(ii)

$\cot \theta$,

(ii) $\cot \theta$,

(iii)

$\text{cosec} \theta$.

(iii) $\text{cosec} \theta$.

Use Pythagoras’ Theorem to find the height:
$\begin{aligned}
\sqrt{{{7}^{2}}-{{2}^{2}}}&=\sqrt{45} \\
=\sqrt{9\cdot 5} \\
=3\sqrt{5}
\end{aligned}$

(i)
(ii)
(iii)

$\begin{aligned}
\sec \theta &=\frac{1}{\cos \theta } \\
& =\frac{7}{2}
\end{aligned}$

$\begin{aligned}
\cot \theta &=\frac{1}{\tan \theta } \\
& =\frac{1}{\frac{3\sqrt{5}}{2}} \\
& =\frac{2}{3\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}} \\
& =\frac{2}{15}\sqrt{5}
\end{aligned}$

$\begin{aligned}
\text{cosec}\theta &=\frac{1}{\sin \theta } \\
& =\frac{1}{\frac{3\sqrt{5}}{7}} \\
& =\frac{7}{3\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}} \\
& =\frac{7}{15}\sqrt{5}
\end{aligned}$

(i)
(ii)
(iii)

$\begin{aligned}
\sec \theta &=\frac{1}{\cos \theta } \\
& =\frac{7}{2}
\end{aligned}$

$\begin{aligned}
\cot \theta &=\frac{1}{\tan \theta } \\
& =\frac{1}{\frac{3\sqrt{5}}{2}} \\
& =\frac{2}{3\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}} \\
& =\frac{2}{15}\sqrt{5}
\end{aligned}$

$\begin{aligned}
\text{cosec}\theta &=\frac{1}{\sin \theta } \\
& =\frac{1}{\frac{3\sqrt{5}}{7}} \\
& =\frac{7}{3\sqrt{5}}\cdot \frac{\sqrt{5}}{\sqrt{5}} \\
& =\frac{7}{15}\sqrt{5}
\end{aligned}$

The principal values of trigonometric functions are those values in the domain, which the function will make exist. The principal values of $x$ are defined as follow.

$y=\cos x$

$0{}^\circ \le x\le 180{}^\circ $ or $0\le x\le \pi $

$y=\sin x$

$-{{90}^{{}^\circ }}\le x\le {{90}^{{}^\circ }}$ or $-\frac{\pi }{2}\le x\le \frac{\pi }{2}$

$y=\tan x$

$-{{90}^{{}^\circ }}\le x\le {{90}^{{}^\circ }}$ or $-\frac{\pi }{2}\le x\le \frac{\pi }{2}$

Practice Question 5

Write down the principal value of ${{\tan }^{-1}}\left( -\sqrt{3} \right)$, leaving your answer in radian as a multiple of $\pi $.

Solution

$\begin{aligned}
{{\tan }^{-1}}\left( -\sqrt{3} \right)&=-60{}^\circ \\
& =-60{}^\circ \times \frac{\pi }{180{}^\circ } \\
& =-\frac{1}{3}\pi
\end{aligned}$

Do sign up for our Free Mini-Courses and try our well-structured curriculum to see how it can help to maximize your learning in mathematics online.

Secondary School Additional Mathematics Free Online Course Sign Up.

You may also find the pricing and plans for our Additional Mathematics unlimited all-access courses here!

Topic List

Free Mini Course

With our online courses, you can learn at your own pace and take your time whenever it’s most convenient for you. Experience learning with us now for free!

Topics included:

O Level | IGCSE | Additional Mathematics

Trigonometric Functions

The Complete Study Guide | Video explanations | Downloadable Worksheets