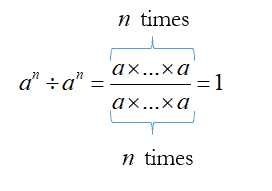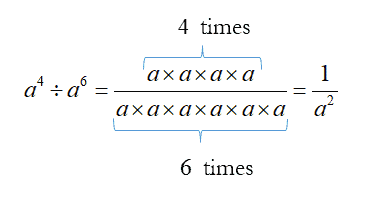- Home
- Study Guides
What Are Indices?
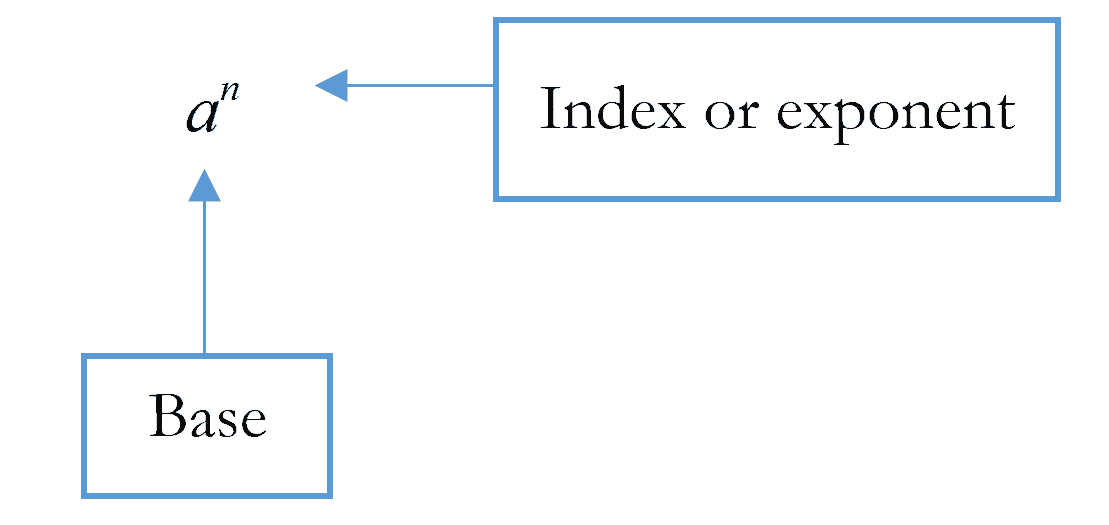
An index is a number multiplied by itself some number of times. The power, also called the index, tells you how many times you have to multiply the number by itself. If you raise a number to the power of $n$, then you multiply that number by itself $n$ times. When a number $a$ is multiplied by itself $n$ times, we can express it as index notation:
It is read as ‘$a$ to the power of $n$’.
Laws of Indices
The laws of indices are a set of techniques to be applied when simplifying expressions containing powers. The purpose of the laws is to enable us to simplify problems of addition, subtraction, multiplication, and division involving powers. They are useful in many branches of mathematics, both for reducing lengthy calculations and for allowing us to work out a solution by inspection. There are $5$ important laws of indices.
In general, if $a$ is real number, and $m$ and $n$ are positive integers, then
Law 1 of Indices (same base)
Law 2 of Indices (same base)
Law 3 of Indices (same base)
Law 1 of Indices (same base)
${{a}^{m}}\times {{a}^{n}}={{a}^{m+n}}$
Example:
${{6}^{4}}\times {{6}^{5}}={{6}^{9}}$
${{a}^{3}}\times {{a}^{4}}={{a}^{7}}$
Law 2 of Indices (same base)
$\frac{{a}^{m}}{{a}^{n}}={{a}^{m-n}}$, if $a \neq 0$.
Example:
$\frac{{{10}^{6}}}{{{10}^{4}}}={{10}^{2}}$
$\frac{{{a}^{7}}}{{{a}^{3}}}={{a}^{4}}$
Law 3 of Indices (same base)
${{({{a}^{m}})}^{n}}={{a}^{mn}}$
Example:
${{\left( {{2}^{5}} \right)}^{2}}={{2}^{10}}$
${{\left( {{a}^{3}} \right)}^{4}}={{a}^{12}}$
If $a$ and $b$ are real numbers, and $n$ is a positive integer, then
Law 4 of Indices (same index)
Law 5 of Indices (same index)
Law 4 of Indices (same index)
${{a}^{n}}\times {{b}^{n}}={{\left( ab \right)}^{n}}$
It can also be written as ${{\left( ab \right)}^{n}}={{a}^{n}}{{b}^{n}}$.
Example:
${{\left( -3 \right)}^{2}}\times {{\left( -4 \right)}^{2}}={{\left( -3\times \left( -4 \right) \right)}^{2}}$
$\left( {{7}^{3}}\times {{2}^{3}} \right)={{\left( 7\times 2 \right)}^{3}}$
Law 5 of Indices (same index)
$\frac{{{a}^{m}}}{{{b}^{m}}}={{\left( \frac{a}{b} \right)}^{m}}$
It can also be written as ${{\left( \frac{a}{b} \right)}^{m}}=\left( \frac{{{a}^{m}}}{{{b}^{m}}} \right)$
Example:
$\frac{{{8}^{3}}}{{{5}^{3}}}={{\left( \frac{8}{5} \right)}^{3}}$
$\frac{{{7}^{3}}}{{{2}^{3}}}={{\left( \frac{7}{2} \right)}^{3}}$
Practice Question 1
Simplify each of the following
(i)
${{a}^{7}}\times {{a}^{3}}$ ÷ ${{\left( {{a}^{3}} \right)}^{2}}$
(i) ${{a}^{7}}\times {{a}^{3}}$÷${{\left( {{a}^{3}} \right)}^{2}}$
(ii)
${{\left( {{2}^{b}} \right)}^{5}}$ ÷ $8{{b}^{2}}$
(ii) ${{\left( {{2}^{b}} \right)}^{5}}$ ÷ $8{{b}^{2}}$
(iii)
${{\left( \frac{3{{x}^{2}}}{{{x}^{3}}} \right)}^{3}}$ ÷ $\frac{27{{x}^{7}}}{{{x}^{21}}}$
(iii) ${{\left( \frac{3{{x}^{2}}}{{{x}^{3}}} \right)}^{3}}$ ÷ $\frac{27{{x}^{7}}}{{{x}^{21}}}$
(iv)
${{\left( {{c}^{2}}d \right)}^{4}}\times {{\left( {{c}^{4}}{{d}^{3}} \right)}^{5}}$
(iv) ${{\left( {{c}^{2}}d \right)}^{4}}\times {{\left( {{c}^{4}}{{d}^{3}} \right)}^{5}}$
(v)
$5{{\left( ef \right)}^{3}}\times 10e{{f}^{2}}$
(v) $5{{\left( ef \right)}^{3}}\times 10e{{f}^{2}}$
(vi)
$16{{m}^{8}}{{n}^{7}}$ ÷ ${{\left( -2{{m}^{3}}{{n}^{2}} \right)}^{2}}$
(vi) $16{{m}^{8}}{{n}^{7}}$ ÷ ${{\left( -2{{m}^{3}}{{n}^{2}} \right)}^{2}}$
(vii)
${{\left( \frac{{{p}^{2}}}{q} \right)}^{6}}\times {{\left( \frac{2{{q}^{2}}}{-3{{p}^{5}}} \right)}^{3}}$
(vii) ${{\left( \frac{{{p}^{2}}}{q} \right)}^{6}}\times {{\left( \frac{2{{q}^{2}}}{-3{{p}^{5}}} \right)}^{3}}$
${{a}^{7}}\times {{a}^{3}}$ ÷ ${{\left( {{a}^{3}} \right)}^{2}}$
$={{a}^{7}}\times {{a}^{3}}$ ÷ ${{a}^{6}}$
$={a}^{7+3-6}$
$={a}^{4}$
${{\left( {{2}^{b}} \right)}^{5}}$ ÷ $8{{b}^{2}}$
$\begin{aligned}
& =\frac{{{\left( 2b \right)}^{5}}}{8{{b}^{2}}} \\
& =\frac{{{2}^{5}}\cdot {{b}^{5}}}{8{{b}^{2}}} \\
& =\frac{{{2}^{5}}}{8}{{b}^{5-2}} \\
& =4{{b}^{3}} \\
\end{aligned}$
${{\left( \frac{3{{x}^{2}}}{{{x}^{3}}} \right)}^{3}}$ ÷ $\frac{27{{x}^{7}}}{{{x}^{21}}}$
$\begin{aligned}
& =\frac{{{3}^{3}}\cdot {{\left( {{x}^{2}} \right)}^{3}}}{{{\left( {{x}^{3}} \right)}^{3}}}\times \frac{{{x}^{21}}}{27{{x}^{7}}} \\
& =\frac{27{{x}^{6}}}{{{x}^{9}}}\times \frac{{{x}^{21}}}{27{{x}^{7}}} \\
& =\frac{{{x}^{6+21}}}{{{x}^{9+7}}} \\
& ={{x}^{27-16}} \\
& ={{x}^{11}} \\
\end{aligned}$
${{\left( {{c}^{2}}d \right)}^{4}}\times {{\left( {{c}^{4}}{{d}^{3}} \right)}^{5}}$
$\begin{aligned}
& ={{\left( {{c}^{2}} \right)}^{4}}{{d}^{4}}\times {{\left( {{c}^{4}} \right)}^{5}}{{\left( {{d}^{3}} \right)}^{5}} \\
& ={{c}^{8}}{{d}^{4}}{{c}^{20}}{{d}^{15}} \\
& ={{c}^{28}}{{d}^{19}} \\
\end{aligned}$
${{a}^{7}}\times {{a}^{3}}$ ÷ ${{\left( {{a}^{3}} \right)}^{2}}$
$={{a}^{7}}\times {{a}^{3}}$ ÷ ${{a}^{6}}$
$={a}^{7+3-6}$
$={a}^{4}$
${{\left( {{2}^{b}} \right)}^{5}}$ ÷ $8{{b}^{2}}$
$\begin{aligned}
& =\frac{{{\left( 2b \right)}^{5}}}{8{{b}^{2}}} \\
& =\frac{{{2}^{5}}\cdot {{b}^{5}}}{8{{b}^{2}}} \\
& =\frac{{{2}^{5}}}{8}{{b}^{5-2}} \\
& =4{{b}^{3}} \\
\end{aligned}$
${{\left( \frac{3{{x}^{2}}}{{{x}^{3}}} \right)}^{3}}$ ÷ $\frac{27{{x}^{7}}}{{{x}^{21}}}$
$\begin{aligned}
& =\frac{{{3}^{3}}\cdot {{\left( {{x}^{2}} \right)}^{3}}}{{{\left( {{x}^{3}} \right)}^{3}}}\times \frac{{{x}^{21}}}{27{{x}^{7}}} \\
& =\frac{27{{x}^{6}}}{{{x}^{9}}}\times \frac{{{x}^{21}}}{27{{x}^{7}}} \\
& =\frac{{{x}^{6+21}}}{{{x}^{9+7}}} \\
& ={{x}^{27-16}} \\
& ={{x}^{11}} \\
\end{aligned}$
${{\left( {{c}^{2}}d \right)}^{4}}\times {{\left( {{c}^{4}}{{d}^{3}} \right)}^{5}}$
$\begin{aligned}
& ={{\left( {{c}^{2}} \right)}^{4}}{{d}^{4}}\times {{\left( {{c}^{4}} \right)}^{5}}{{\left( {{d}^{3}} \right)}^{5}} \\
& ={{c}^{8}}{{d}^{4}}{{c}^{20}}{{d}^{15}} \\
& ={{c}^{28}}{{d}^{19}} \\
\end{aligned}$
$5{{\left( ef \right)}^{3}}\times 10e{{f}^{2}}$
$\begin{aligned}
& =5{{e}^{3}}{{f}^{3}}\times 10{{e}^{1}}{{f}^{2}} \\
& =50{{e}^{3+1}}{{f}^{3+2}} \\
& =50{{e}^{4}}{{f}^{5}} \\
\end{aligned}$
$16{{m}^{8}}{{n}^{7}}$ ÷ ${{\left( -2{{m}^{3}}{{n}^{2}} \right)}^{2}}$
$\begin{aligned}
& =\frac{16{{m}^{8}}{{n}^{7}}}{{{\left( -2{{m}^{3}}{{n}^{3}} \right)}^{2}}} \\
& =\frac{16{{m}^{8}}{{n}^{7}}}{{{\left( -2 \right)}^{2}}{{\left( {{m}^{3}} \right)}^{2}}{{\left( {{n}^{2}} \right)}^{2}}} \\
& =\frac{16{{m}^{8}}{{n}^{7}}}{4{{m}^{6}}{{n}^{4}}} \\
& =\frac{16}{4}{{m}^{8-6}}{{n}^{7-4}} \\
& =4{{m}^{2}}{{n}^{3}} \\
\end{aligned}$
${{\left( \frac{{{p}^{2}}}{q} \right)}^{6}}\times {{\left( \frac{2{{q}^{2}}}{-3{{p}^{5}}} \right)}^{3}}$
$\begin{aligned}
& =\frac{{{\left( {{p}^{2}} \right)}^{6}}}{{{q}^{6}}}\times \frac{{{2}^{3}}{{\left( {{q}^{2}} \right)}^{3}}}{{{\left( -3 \right)}^{3}}{{\left( {{p}^{5}} \right)}^{3}}} \\
& =\frac{{{p}^{12}}}{{{q}^{6}}}\times \frac{8{{q}^{6}}}{-27{{p}^{15}}} \\
& =-\frac{8}{27}\cdot {{p}^{12-15}} \\
& =-\frac{8}{27}{{p}^{-3}} \\
\end{aligned}$
$5{{\left( ef \right)}^{3}}\times 10e{{f}^{2}}$
$\begin{aligned}
& =5{{e}^{3}}{{f}^{3}}\times 10{{e}^{1}}{{f}^{2}} \\
& =50{{e}^{3+1}}{{f}^{3+2}} \\
& =50{{e}^{4}}{{f}^{5}} \\
\end{aligned}$
$16{{m}^{8}}{{n}^{7}}$ ÷ ${{\left( -2{{m}^{3}}{{n}^{2}} \right)}^{2}}$
$\begin{aligned}
& =\frac{16{{m}^{8}}{{n}^{7}}}{{{\left( -2{{m}^{3}}{{n}^{3}} \right)}^{2}}} \\
& =\frac{16{{m}^{8}}{{n}^{7}}}{{{\left( -2 \right)}^{2}}{{\left( {{m}^{3}} \right)}^{2}}{{\left( {{n}^{2}} \right)}^{2}}} \\
& =\frac{16{{m}^{8}}{{n}^{7}}}{4{{m}^{6}}{{n}^{4}}} \\
& =\frac{16}{4}{{m}^{8-6}}{{n}^{7-4}} \\
& =4{{m}^{2}}{{n}^{3}} \\
\end{aligned}$
${{\left( \frac{{{p}^{2}}}{q} \right)}^{6}}\times {{\left( \frac{2{{q}^{2}}}{-3{{p}^{5}}} \right)}^{3}}$
$\begin{aligned}
& =\frac{{{\left( {{p}^{2}} \right)}^{6}}}{{{q}^{6}}}\times \frac{{{2}^{3}}{{\left( {{q}^{2}} \right)}^{3}}}{{{\left( -3 \right)}^{3}}{{\left( {{p}^{5}} \right)}^{3}}} \\
& =\frac{{{p}^{12}}}{{{q}^{6}}}\times \frac{8{{q}^{6}}}{-27{{p}^{15}}} \\
& =-\frac{8}{27}\cdot {{p}^{12-15}} \\
& =-\frac{8}{27}{{p}^{-3}} \\
\end{aligned}$
Zero Indices
Any number raised to the power zero will yield a value equal to one. In general, for $n=0$, we define
$a^0=1$
where $a$ is any real number and $a\neq0$.
Suppose we are required to simplify $\left( \frac{{{a}^{5}}}{{{a}^{5}}} \right)$,
Using Law 2 of Indices, $\left( \frac{{{a}^{5}}}{{{a}^{5}}} \right)={a}^{5-5}=a^0$,
Therefore, $a^0=1$
Examples of Zero Indices:
$13^0=1$
$\left(-\frac{3}{7} \right)^0=1$
$\begin{aligned}5a^0&=5(1)\\&=5\end{aligned}$
Negative Indices
The negative index notation is a convenient way to deal with situations where the power is a number less than $0$. What happens if we have a number with a negative power? Generally, we define it as
${a}^{-n}=\frac{1}{a^n}$
where $a$ is any real number and $a\neq 0$.
To simplify $\left( \frac{{{a}^{4}}}{{{a}^{6}}} \right)$,
We can use Law 2 of Indices, $\left( \frac{{{a}^{4}}}{{{a}^{6}}} \right)={a}^{4-6}={a}^{-2}$
So what is ${a}^{-2}$?
Therefore, ${a}^{-2}=\frac{1}{{a}^{2}}$
Examples of Negative Indices:
$\begin{aligned}{5}^{-3}&=\frac{1}{5^3}\\&=\frac{1}{125}\end{aligned}$
$\begin{aligned}
 {{2}^{0}}+{{2}^{-3}}&=1+\frac{1}{{{2}^{3}}} \\
& =1+\frac{1}{8} \\
& =1\frac{1}{8}
\end{aligned}$
| $\begin{aligned} {{\left( \frac{2}{3} \right)}^{-3}}&=\frac{1}{{{\left( \frac{2}{3} \right)}^{3}}} \\ & =\frac{1}{\frac{8}{27}} \\ & =\frac{27}{8} \\ & =3\frac{3}{8} \end{aligned}$ |
OR | Faster Method: $\begin{aligned} {{\left( \frac{2}{3} \right)}^{-3}}&={{\left( \frac{3}{2} \right)}^{3}} \\ & =\frac{27}{8} \\ & =3\frac{3}{8} \end{aligned}$ |
${{\left( \frac{a}{b} \right)}^{-n}}={{\left( \frac{b}{a} \right)}^{n}}$
We can now extend all the $5$ laws of indices to include all integer indices. (positive, zero, and negative)
Practice Question 2
Simplify each of the following, giving your answers in positive index notation.
(i)
$18{{a}^{-6}}$ ÷ $3{{\left( {{a}^{-2}} \right)}^{2}}$
(i) $18{{a}^{-6}}$ ÷ $3{{\left( {{a}^{-2}} \right)}^{2}}$
(ii)
$5{{b}^{0}}\times 3{{\left( {{b}^{-2}} \right)}^{2}}$
(ii) $5{{b}^{0}}\times 3{{\left( {{b}^{-2}} \right)}^{2}}$
(iii)
${{\left( 3{{c}^{2}}{{d}^{-2}} \right)}^{2}}$
(iii) ${{\left( 3{{c}^{2}}{{d}^{-2}} \right)}^{2}}$
(iv)
${{\left( \frac{{{e}^{2}}{{f}^{-1}}}{2} \right)}^{-3}}$
(iv) ${{\left( \frac{{{e}^{2}}{{f}^{-1}}}{2} \right)}^{-3}}$
$18{{a}^{-6}}$ ÷ $3{{\left( {{a}^{-2}} \right)}^{2}}$
$\begin{aligned}
& =18\left( \frac{1}{{{a}^{6}}} \right)\times \frac{1}{3{{\left( {{a}^{-2}} \right)}^{2}}} \\
& =6\left( \frac{1}{{{a}^{6}}} \right)\times \frac{1}{{{a}^{-4}}} \\
& =6\left[ \frac{1}{{{a}^{6-4}}} \right] \\
& =\frac{6}{{{a}^{2}}} \\
\end{aligned}$
$5{{b}^{0}}\times 3{{\left( {{b}^{-2}} \right)}^{2}}$
$\begin{aligned}
& =5\left( 1 \right)\times 3\left( {{b}^{-4}} \right) \\
& =15{{b}^{-4}} \\
& =15\left( \frac{1}{{{b}^{4}}} \right) \\
& =\frac{15}{{{b}^{4}}} \\
\end{aligned}$
${{\left( 3{{c}^{2}}{{d}^{-2}} \right)}^{2}}$
$\begin{aligned}
& ={{3}^{2}}{{\left( {{c}^{2}} \right)}^{2}}{{\left( {{d}^{-2}} \right)}^{2}} \\
& =9{{c}^{4}}{{d}^{-4}} \\
& =9{{c}^{4}}\left( \frac{1}{{{d}^{4}}} \right) \\
& =\frac{9{{c}^{4}}}{{{d}^{4}}} \\
\end{aligned}$
${{\left( \frac{{{e}^{2}}{{f}^{-1}}}{2} \right)}^{-3}}$
$\begin{aligned}
& ={{\left( \frac{2}{{{e}^{2}}{{f}^{-1}}} \right)}^{3}} \\
& =\frac{{{2}^{3}}}{{{\left( {{e}^{2}} \right)}^{3}}{{\left( {{f}^{-1}} \right)}^{3}}} \\
& =\frac{8}{{{e}^{6}}{{f}^{-3}}} \\
& =\frac{8}{{{e}^{6}}}\cdot \frac{1}{{{f}^{-3}}} \\
& =\frac{8}{{{e}^{6}}}\cdot {{\left( \frac{1}{f} \right)}^{-3}} \\
& =\frac{8}{{{e}^{6}}}{{\left( \frac{f}{1} \right)}^{3}} \\
& =\frac{8{{f}^{3}}}{{{e}^{6}}} \\
\end{aligned}$
$18{{a}^{-6}}$ ÷ $3{{\left( {{a}^{-2}} \right)}^{2}}$
$\begin{aligned}
& =18\left( \frac{1}{{{a}^{6}}} \right)\times \frac{1}{3{{\left( {{a}^{-2}} \right)}^{2}}} \\
& =6\left( \frac{1}{{{a}^{6}}} \right)\times \frac{1}{{{a}^{-4}}} \\
& =6\left[ \frac{1}{{{a}^{6-4}}} \right] \\
& =\frac{6}{{{a}^{2}}} \\
\end{aligned}$
$5{{b}^{0}}\times 3{{\left( {{b}^{-2}} \right)}^{2}}$
$\begin{aligned}
& =5\left( 1 \right)\times 3\left( {{b}^{-4}} \right) \\
& =15{{b}^{-4}} \\
& =15\left( \frac{1}{{{b}^{4}}} \right) \\
& =\frac{15}{{{b}^{4}}} \\
\end{aligned}$
${{\left( 3{{c}^{2}}{{d}^{-2}} \right)}^{2}}$
$\begin{aligned}
& ={{3}^{2}}{{\left( {{c}^{2}} \right)}^{2}}{{\left( {{d}^{-2}} \right)}^{2}} \\
& =9{{c}^{4}}{{d}^{-4}} \\
& =9{{c}^{4}}\left( \frac{1}{{{d}^{4}}} \right) \\
& =\frac{9{{c}^{4}}}{{{d}^{4}}} \\
\end{aligned}$
${{\left( \frac{{{e}^{2}}{{f}^{-1}}}{2} \right)}^{-3}}$
$\begin{aligned}
& ={{\left( \frac{2}{{{e}^{2}}{{f}^{-1}}} \right)}^{3}} \\
& =\frac{{{2}^{3}}}{{{\left( {{e}^{2}} \right)}^{3}}{{\left( {{f}^{-1}} \right)}^{3}}} \\
& =\frac{8}{{{e}^{6}}{{f}^{-3}}} \\
& =\frac{8}{{{e}^{6}}}\cdot \frac{1}{{{f}^{-3}}} \\
& =\frac{8}{{{e}^{6}}}\cdot {{\left( \frac{1}{f} \right)}^{-3}} \\
& =\frac{8}{{{e}^{6}}}{{\left( \frac{f}{1} \right)}^{3}} \\
& =\frac{8{{f}^{3}}}{{{e}^{6}}} \\
\end{aligned}$
Positive ${n}^{th}$ Root
An expression that involves the radical sign $\sqrt[n]{\square }$ is called the radical expression. The radical sign is a square root symbol. It is read as “root,” and it means the principal square root. The number inside the radical sign is called the radicand. It must be a real number, not a complex number. The letters on top of the radical sign are called index letters and signify coefficients of powers of the radicand in the expression.
If $a$ is a positive number such that $a={b}^{n}$ for some positive integer $b$, then $b$ is the positive ${n}^{th}$ root of $a$ and we write as:
$b=\sqrt[n]{a}$
Practice Question 3
Evaluate each of the following without the use of a calculator.
(i)
$\sqrt[4]{16}$
(i) $\sqrt[4]{16}$
(ii)
$\sqrt[3]{\frac{27}{125}}$
(ii) $\sqrt[3]{\frac{27}{125}}$
$\sqrt[4]{16}$
$\begin{aligned}
& =\sqrt[4]{{{2}^{4}}} \\
& =2 \\
\end{aligned}$
$\sqrt[3]{\frac{27}{125}}$
$\begin{aligned}
& =\sqrt[3]{\frac{{{3}^{3}}}{{{5}^{3}}}} \\
& =\frac{\sqrt[3]{{{3}^{3}}}}{\sqrt[3]{{{5}^{3}}}} \\
& =\frac{3}{5} \\
\end{aligned}$
$\sqrt[4]{16}$
$\begin{aligned}
& =\sqrt[4]{{{2}^{4}}} \\
& =2 \\
\end{aligned}$
$\sqrt[3]{\frac{27}{125}}$
$\begin{aligned}
& =\sqrt[3]{\frac{{{3}^{3}}}{{{5}^{3}}}} \\
& =\frac{\sqrt[3]{{{3}^{3}}}}{\sqrt[3]{{{5}^{3}}}} \\
& =\frac{3}{5} \\
\end{aligned}$
Rational Indices
Since we have already extended all the 5 laws of indices to include all integer indices, is it possible to have an index that is not an integer? What happens if we encounter indices that are non-integer rational numbers? How do we solve them? For instance, what is $3^{\frac{1}{2}}$ and $3^{\frac{1}{3}}$ equal to?
- Let $p=3^{\frac{1}{2}}$.
- Then square both sides.
We will get ${{\left( p \right)}^{2}}={{\left( {{3}^{\frac{1}{2}}} \right)}^{2}}$. - Applying Law $3$ of Indices,
$\begin{aligned}
 {{p}^{2}}&={{3}^{1}} \\
 p&=\sqrt{3}
\end{aligned}$ - From the previous lesson, we know that when $a={{b}^{n}}$, then $b=\sqrt[n]{a}$.
- Therefore, $p=\sqrt{3}$.
- This means that $3^{\frac{1}{2}}=\sqrt{3}$.
- Let $p=3^{\frac{1}{3}}$.
- Then cube both sides.
We will get ${{\left( p \right)}^{3}}={{\left( {{3}^{\frac{1}{3}}} \right)}^{3}}$. - Applying Law $3$ of Indices, $p^3=3$.
- From the previous lesson, we know that when $a={{b}^{n}}$, then $b=\sqrt[n]{a}$.
- Therefore, $p=\sqrt[3]{3}$.
- This means that $3^{\frac{1}{3}}=\sqrt[3]{3}$.
If $a$ is a positive integer, we can define thatÂ
${a}^{\frac{1}{n}}=\sqrt[n]{a}$
if $a>0$.
Examples:
${7}^{\frac{1}{5}}=\sqrt[5]{7}$
${10}^{\frac{1}{11}}=\sqrt[11]{10}$
Practice Question 4
Rewrite each of the following in radical form and hence evaluate the results without using a calculator.
(i)
${{81}^{\frac{1}{4}}}$
(i) ${{81}^{\frac{1}{4}}}$
(ii)
${{8}^{-\frac{1}{3}}}$
(ii) ${{8}^{-\frac{1}{3}}}$
Tips: Generally, if $m$ and $n$ are positive integers,Â
${{a}^{\frac{m}{n}}}=\sqrt[n]{{{a}^{m}}}$ or ${{\left( \sqrt[n]{a} \right)}^{m}}$
if $a>0$.
${{81}^{\frac{1}{4}}}$
$\begin{aligned}
& =\sqrt[4]{81} \\
& =\sqrt[4]{{{3}^{4}}} \\
& =3 \\
\end{aligned}$
${{8}^{-\frac{1}{3}}}$
$\begin{aligned}
& ={{\left( {{8}^{-1}} \right)}^{\frac{1}{3}}} \\
& ={{\left( \frac{1}{8} \right)}^{\frac{1}{3}}} \\
& =\frac{{{1}^{\frac{1}{3}}}}{{{8}^{\frac{1}{3}}}} \\
& =\frac{\sqrt[3]{1}}{\sqrt[3]{8}} \\
& =\frac{1}{\sqrt[3]{{{2}^{3}}}} \\
& =\frac{1}{2} \\
\end{aligned}$
${{81}^{\frac{1}{4}}}$
$\begin{aligned}
& =\sqrt[4]{81} \\
& =\sqrt[4]{{{3}^{4}}} \\
& =3 \\
\end{aligned}$
${{8}^{-\frac{1}{3}}}$
$\begin{aligned}
& ={{\left( {{8}^{-1}} \right)}^{\frac{1}{3}}} \\
& ={{\left( \frac{1}{8} \right)}^{\frac{1}{3}}} \\
& =\frac{{{1}^{\frac{1}{3}}}}{{{8}^{\frac{1}{3}}}} \\
& =\frac{\sqrt[3]{1}}{\sqrt[3]{8}} \\
& =\frac{1}{\sqrt[3]{{{2}^{3}}}} \\
& =\frac{1}{2} \\
\end{aligned}$
Equations involving Indices
Next, if we have an equation in which the unknown, $x$ is the index, how do we solve this?Â
$a^x=b$
Tips: Change both sides to the same base. (We can use prime factorization to break apart the numbers so that they behave the same)
Practice Question 5
Solve each of the equation
(i)
${2}^{x}=8$
(i) ${2}^{x}=8$
(ii)
${5}^{y}=\frac{1}{25}$
(ii) ${5}^{y}=\frac{1}{25}$
(iii)
${9}^{x}=27$
(iii) ${9}^{x}=27$
$\begin{aligned}
 {{2}^{x}}&=8 \\
 {{2}^{x}}&={{2}^{3}} \\
 x&=3
\end{aligned}$
$\begin{aligned}
 {{5}^{y}}&=\frac{1}{25} \\
 {{5}^{y}}&={{5}^{-2}} \\
y&=-2
\end{aligned}$
$\begin{aligned}
 {{9}^{z}}&=27 \\
 {{\left( {{3}^{2}} \right)}^{z}}&={{3}^{3}} \\
 {{3}^{2z}}&={{3}^{3}} \\
 2z&=3 \\
 z&=\frac{3}{2} \\
 z&=1\frac{1}{2}
\end{aligned}$
$\begin{aligned}
 {{2}^{x}}&=8 \\
 {{2}^{x}}&={{2}^{3}} \\
 x&=3
\end{aligned}$
$\begin{aligned}
 {{5}^{y}}&=\frac{1}{25} \\
 {{5}^{y}}&={{5}^{-2}} \\
y&=-2
\end{aligned}$
$\begin{aligned}
 {{9}^{z}}&=27 \\
 {{\left( {{3}^{2}} \right)}^{z}}&={{3}^{3}} \\
 {{3}^{2z}}&={{3}^{3}} \\
 2z&=3 \\
 z&=\frac{3}{2} \\
 z&=1\frac{1}{2}
\end{aligned}$
Solving Exponential Equations Using Substitution
Suppose you have to solve a complicated question with exponential equations, you can often make the question simpler by a process called substitution. The idea is to replace a hard-to-solve equation with an easier one.
It is called substitution because what gets substituted is a simpler expression that can then be solved using more basic math skills. You can substitute any expression for any variable in an equation as long as you don’t change the value of whatever expression you’re solving for.
Practice Question 6
Use an appropriate substitution, or otherwise, solve ${7}^{2x+1}+20({7}^{x})=3$.
$\begin{aligned}
{{7}^{2x+1}}+20\left( {{7}^{x}} \right)&=3 \\
 {{7}^{2x}}\cdot 7+20\left( {{7}^{x}} \right)&=3 \\
 7{{\left( {{7}^{x}} \right)}^{2}}+20\left( {{7}^{x}} \right)-3&=0
\end{aligned}$
Let $u={{7}^{x}}$,
$\begin{aligned}
 7{{u}^{2}}+20u-3&=0 \\
 \left( 7u-1 \right)\left( u+3 \right)&=0 \\
 u&=\frac{1}{7}\,\,\text{or}\,\,-3
\end{aligned}$
Replace $u$ with ${7}^{x}$:
${{7}^{x}}=\frac{1}{7}\,\,\text{or}\,\,-3$ (rej, as ${{7}^{x}}>0$)
$\begin{aligned}
 {{7}^{x}}&={{7}^{-1}} \\
 x&=-1
\end{aligned}$
Simultaneous Exponential Equations
Now that we’ve seen the different types of exponential functions, we generally have the idea of how to solve equations involving them. In this section, we will learn how to solve simultaneous exponential equations.
Remember that in order to solve the simultaneous equations, we need to make sure that all base values in the equations are the same.
Practice Question 7
Solve the simultaneous equations,
$\begin{aligned}
 {{4}^{x}}\left( {{2}^{y}} \right)&=\frac{{{2}^{11}}}{{{16}^{y}}} \\
 {{5}^{x}}\left( {{5}^{x-6y}} \right)&=1
\end{aligned}$
$\begin{aligned}
 {{4}^{x}}\left( {{2}^{y}} \right)&=\frac{{{2}^{11}}}{{{16}^{y}}}—(1) \\
 {{5}^{x}}\left( {{5}^{x-6y}} \right)&=1—(2) \\
\end{aligned}$
From (1):
$\begin{aligned}
 {{4}^{x}}\left( {{2}^{y}} \right)&=\frac{{{2}^{11}}}{{{16}^{y}}} \\
 {{\left( {{2}^{2}} \right)}^{x}}\cdot \left( {{2}^{y}} \right)&=\frac{{{2}^{11}}}{{{\left( {{2}^{4}} \right)}^{y}}} \\
 {{2}^{2x}}\cdot {{2}^{y}}&=\frac{{{2}^{11}}}{{{2}^{4y}}} \\
 {{2}^{2x+y}}&={{2}^{11-4y}} \\
 2x+y&=11-4y \\
 2x&=11-5y—(3)
\end{aligned}$
From (2):
$\begin{aligned}
 {{5}^{x}}\left( {{5}^{x-6y}} \right)&=1 \\
 {{5}^{x+\left( x-6y \right)}}&={{5}^{0}} \\
 x+x-6y&=0 \\
 2x&=6y \\
 x&=3y—(4)
\end{aligned}$
Substitute (4) into (3):
$\begin{aligned}
 2\left( 3y \right)&=11-5y \\
 6y&=11-5y \\
 11y&=11 \\
 y&=1
\end{aligned}$
$\therefore y=1,x=3$
Do sign up for our Free Mini-Courses and try our well-structured curriculum to see how it can help to maximize your learning in mathematics online.
Secondary School Additional Mathematics Free Online Course Sign Up.
You may also find the pricing and plans for our Additional Mathematics unlimited all-access courses here!
Topic List
Free Mini Course
With our online courses, you can learn at your own pace and take your time whenever it’s most convenient for you. Experience learning with us now for free!
Topics included:
- Derivative as a Gradient Function
- Chain Rule
- Problems involving Tangents and Normals
- Connected Rate of Change Involving Area