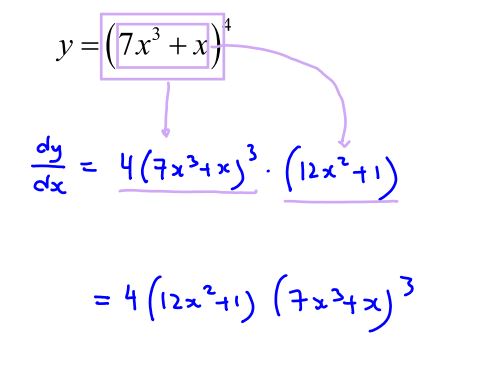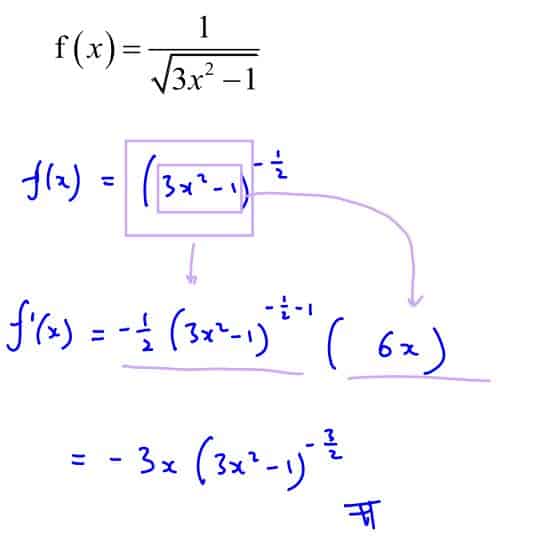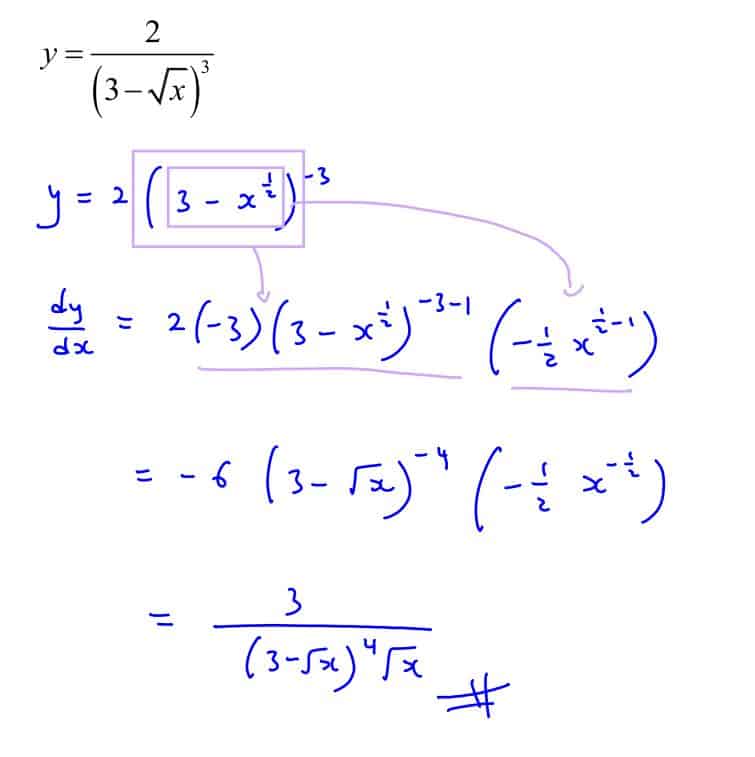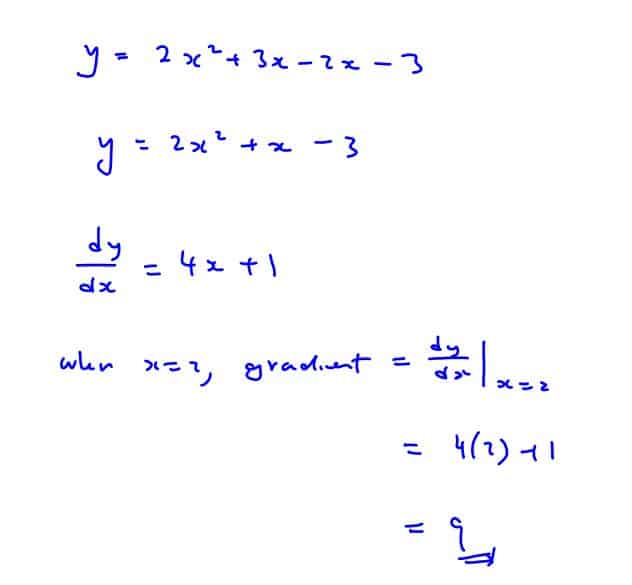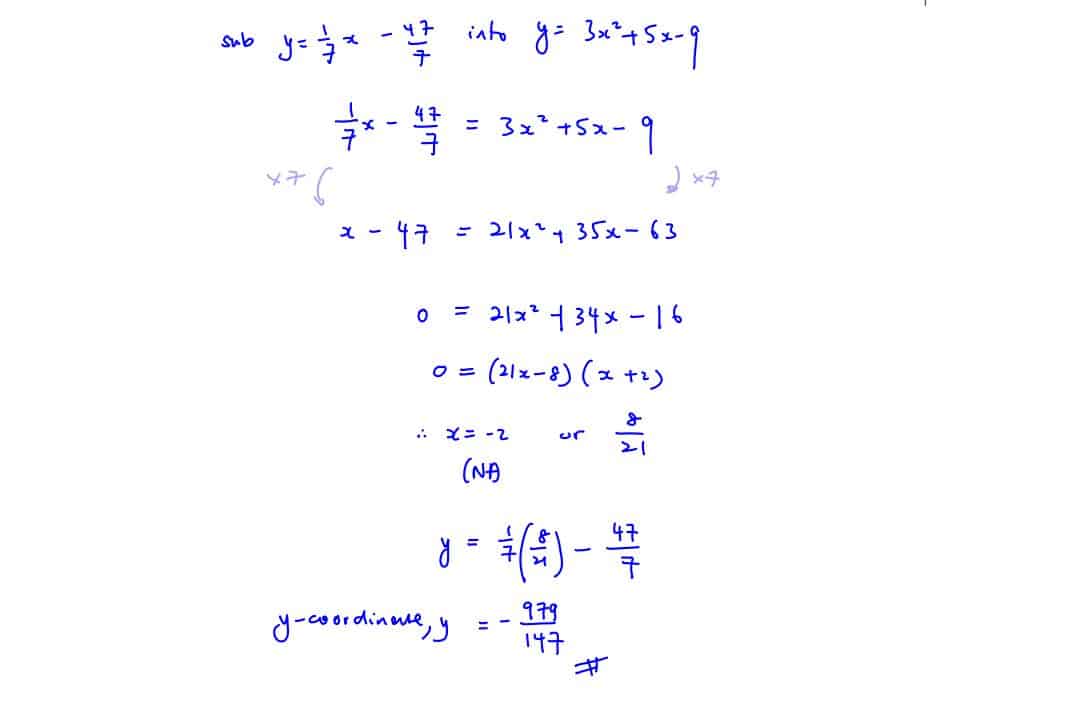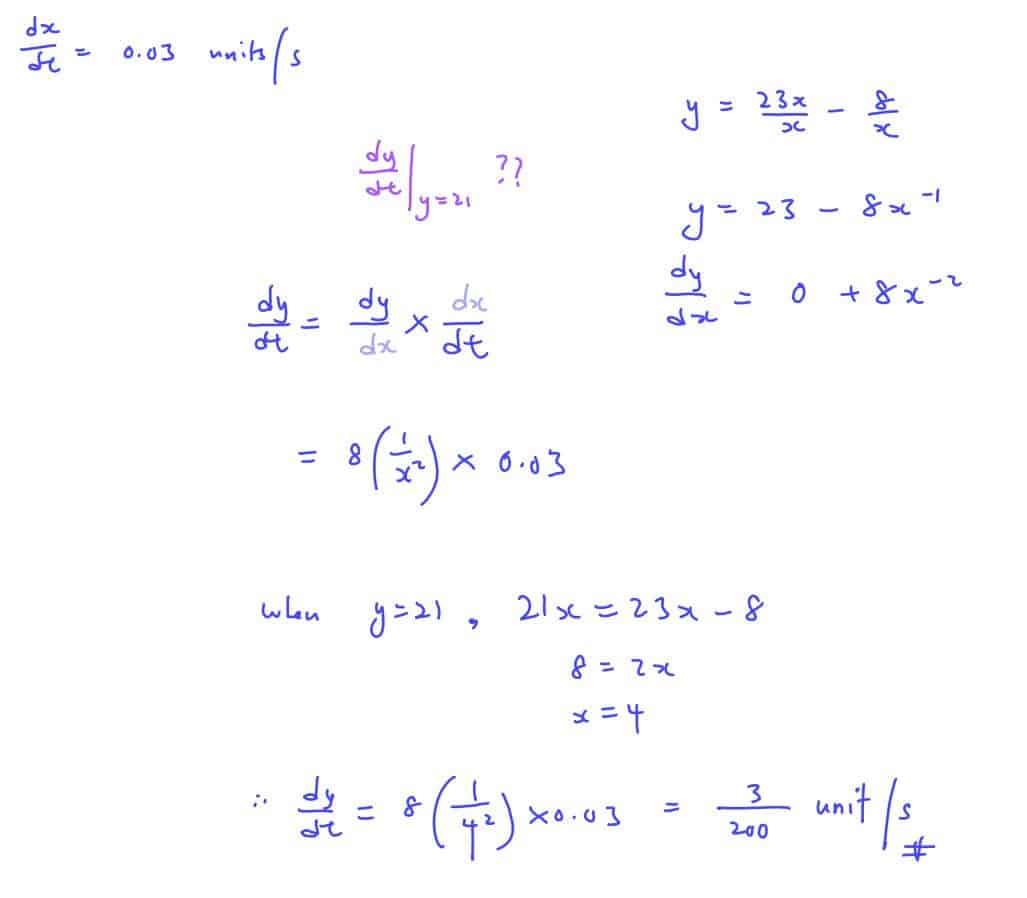- Home
- Study Guides
Differentiation is the fundamental practice of mathematics. It directly relates to the knowledge we acquired during Elementary Math, which indirectly teaches us how to reason about concepts by changing from one representation to another. Differentiation gives us the ability to isolate and measure values between two variables instead of just their sum or average. This article aims to help you learn how to do differentiation in a way that will be fastest for you.
Differentiation is a math topic that can be found in many mathematics syllabi such as the IGCSE Additional Mathematics (0606) and Singapore SEAB Additional Mathematics.
Differentiation - Formula and Its Application
Calculus is a branch of mathematics that studies the continuous change between two variables. Calculus can be further classified into two kinds: differential and integral calculus. Differentiation in calculus is a key concept used to determine instantaneous rates of change. Instantaneous rate of change is the measure of how quickly the new value is affecting the old value. In this article, we will focus on exploring how to differentiate and provide several real-life differentiation examples for you to practice.
What Are The Rules of Differentiation?
Derivative As Gradient Function
Gradient functions are used in math and graphing, and they’re also the most basic function in linear and polynomial regression. The gradient function is a way to describe a slope by showing the height of each degree of ascent (or descent) as a linear function of $x$, with the suffix indicating the direction (positive or negative). A positive gradient indicates that as you approach the endpoint on the $x$-axis, the $y$-axis points go up; a negative gradient indicates that as you approach the endpoint on the $x$-axis, the $y$-axis points go down.
So how do we calculate the gradient function? To make a gradient function, you pick an $x$-axis value (called the “endpoint”) and then sketch every possible $y$-axis point that goes up (or down) with a given slope.
Derivative As Power Functions
How do we find the gradient function of a power function?
Power Rule is a relatively straightforward formula that helps to find the derivative of a power function, a function that has a variable base raised to a fixed real number.
Here are some examples of power functions: $\text{f}\left( x \right)=x,\text{g}\left( x \right)={{x}^{3}},\text{h}\left( x \right)=\frac{1}{x}$
To find the derivative of power functions, we can use this formula:
$\frac{\text{d}}{\text{d}x}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$, where $n$ is a constant
If it is ${x}^{n}$, we can bring the power, $n$, to the front of the $x$, and then minus 1 from the power.
Derivative As Power Functions
How do we find the gradient function of a power function?
Power Rule is a relatively straightforward formula that helps to find the derivative of a power function, a function that has a variable base raised to a fixed real number.
Here are some examples of power functions: $\text{f}\left( x \right)=x,\text{g}\left( x \right)={{x}^{3}},\text{h}\left( x \right)=\frac{1}{x}$
To find the derivative of power functions, we can use this formula:
$\frac{\text{d}}{\text{d}x}\left( {{x}^{n}} \right)=n{{x}^{n-1}}$, where $n$ is a constant
If it is ${x}^{n}$, we can bring the power, $n$, to the front of the $x$, and then minus 1 from the power.
Scalar Multiple
Now, how will we do it if there is a constant in front of the power function? Let’s explore another concept which is called the Scalar Multiple.
$\frac{\text{d}}{\text{d}x}(k{{x}^{n}})=k\frac{\text{d}}{\text{d}x}({{x}^{n}})=kn{{x}^{n-1}}$, where $k$ is a constant.
The constant will not affect the process of differentiation. In fact, we could just take the constant out and differentiate the remaining function according to the appropriate rule. The constant stays until the last step where we multiply the constant with the answer. Simplify and you will get the final answer!
Take note: It has to be a constant. Only constant could be brought out!
Addition and Subtraction Rule
Next, how do we differentiate if there is an addition or subtraction sign between the terms?
$\begin{aligned}
\frac{\text{d}}{\text{d}x}(k{{x}^{n}}+q{{x}^{m}})&=k\frac{\text{d}}{\text{d}x}({{x}^{n}})+q\frac{\text{d}}{\text{d}x}({{x}^{m}}) \\
& =kn{{x}^{n-1}}+qm{{x}^{m-1}}
\end{aligned}$,
where $k$ and $q$ are a constants.
Even though this might look complicated at first, but we can differentiate each term independently. The addition and subtraction do not affect the differentiation process.
Addition and Subtraction Rule
Next, how do we differentiate if there is an addition or subtraction sign between the terms?
$\begin{aligned}
\frac{\text{d}}{\text{d}x}(k{{x}^{n}}+q{{x}^{m}})&=k\frac{\text{d}}{\text{d}x}({{x}^{n}})+q\frac{\text{d}}{\text{d}x}({{x}^{m}}) \\
& =kn{{x}^{n-1}}+qm{{x}^{m-1}}
\end{aligned}$,
where $k$ and $q$ are a constants.
Even though this might look complicated at first, but we can differentiate each term independently. The addition and subtraction do not affect the differentiation process.
Chain Rule
The Chain Rule is a quite fundamental rule in differentiation, which reveals how to find the derivative of a composite function.
$\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}\times \frac{\text{d}u}{\text{d}x}$
The general rule for finding the derivative of a composite function is to:
- Identify the nested function and let the nested function be variable $u$ .
- Calculate the derivative of the nested function, $\frac{\text{d}u}{\text{d}x}$.
- Convert the outer function $y$ in terms of $u$.
- Calculate the derivative of the outer function, $\frac{\text{d}y}{\text{d}u}$.
- Substitute the derivatives into the formula: $\frac{\text{d}y}{\text{d}x}=\frac{\text{d}y}{\text{d}u}\times \frac{\text{d}u}{\text{d}x}$
- Since $u$ is something that we introduce into the equation, we have to substitute the original function back for the variable $u$.
- Simplify to get the final answer.
If you are looking for a faster solution to differentiate a composite function, you can also try this method $\rightarrow$
- Identify the nested function and the outer function.
- Calculate the derivative of the outer function as an entity.
- Calculate the derivative of the nested function.
- Multiply the derivatives to get the final answer.
Practice Question 1
Find the derivative of each of the following,
(a)
$y={{\left( 7{{x}^{3}}+x \right)}^{4}}$
(b)
$\text{f}\left( x \right)=\frac{1}{\sqrt{3{{x}^{2}}-1}}$
(c)
$y=\frac{2}{{{\left( 3-\sqrt{x} \right)}^{3}}}$
- (a)
- (b)
- (c)
- (a)
- (b)
- (c)
Product Rule
The Product Rule of Differentiation is another very important rule that helps us find the derivatives of a product from the multiplication of two variables.
$\frac{\text{d}}{\text{d}x}\left( uv \right)=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$
How to differentiate using the Product Rule:
- Multiply the first term with the derivative of the second term.
- Add the second term multiplied by the derivative of the first term to the first product.
Product Rule
The Product Rule of Differentiation is another very important rule that helps us find the derivatives of a product from the multiplication of two variables.
$\frac{\text{d}}{\text{d}x}\left( uv \right)=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}$
How to differentiate using the Product Rule:
- Multiply the first term with the derivative of the second term.
- Add the second term multiplied by the derivative of the first term to the first product.
Practice Question 2
Differentiate $\sqrt{x}{{({{x}^{2}}+2)}^{5}}$ with respect to $x$.
Quotient Rule
What happens if you have to find the derivatives of the quotients of two variables?
$\frac{\text{d}}{\text{d}x}\left( \frac{u}{v} \right)=\frac{v\frac{\text{du}}{\text{d}x}-u\frac{\text{dv}}{\text{d}x}}{{{v}^{2}}}$
How to differentiate using the Quotient Rule?
- Multiply the denominator with the derivative of the numerator.
- Minus the product of the numerator and the derivative of the denominator.
- Divide all with the square of the denominator.
Practice Question 3
Find the derivative of $y=\frac{x+1}{\sqrt{3{{x}^{2}}-1}}$.
Applications of Differentiation
Gradient of Curve
It is very easy to find the gradient of a function when you have a situation in which a tangent line is easy to find. But finding the gradient in most situations with a complicated equation is tricky. A tangent line does not always give you enough information. Fortunately, there is another way of getting information about the slope of a curve in the plane. Instead of drawing a tangent line, we could use differentiation to find the answer! The difference here is not that it’s harder; it’s that it requires fewer steps. To an onlooker, this difference would seem negligible. But if you look at how much time you spend solving problems, you’ll find that lots of time can be saved if you solve using derivatives. Differentiation is a useful trick because it reduces a problem to a calculation that can be done by hand much faster than by drawing a tangent line.
Practice Question 4
Find the gradient of the curve $y=\left( x-1 \right)\left( 2x+3 \right)$ at $x=2$.
Practice Question 5
Finding the Unknowns when given the gradient
The curve $y=a{{x}^{2}}+bx$ has a gradient of $2$ at the point $\left( 2,0 \right)$. Find the values of $a$ and $b$.
Practice Question 6
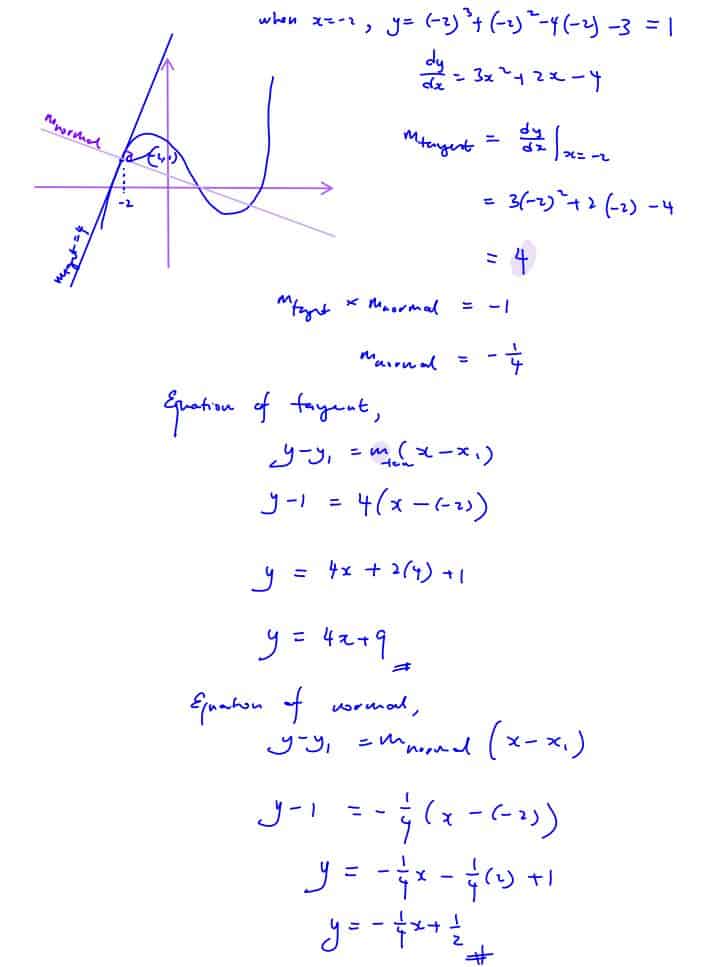
Equations of Tangents and Normal to Curve
Find the equation of the tangent and the normal to the curve $y={{x}^{3}}+{{x}^{2}}-4x-3$ at the point where $x=-2$ .
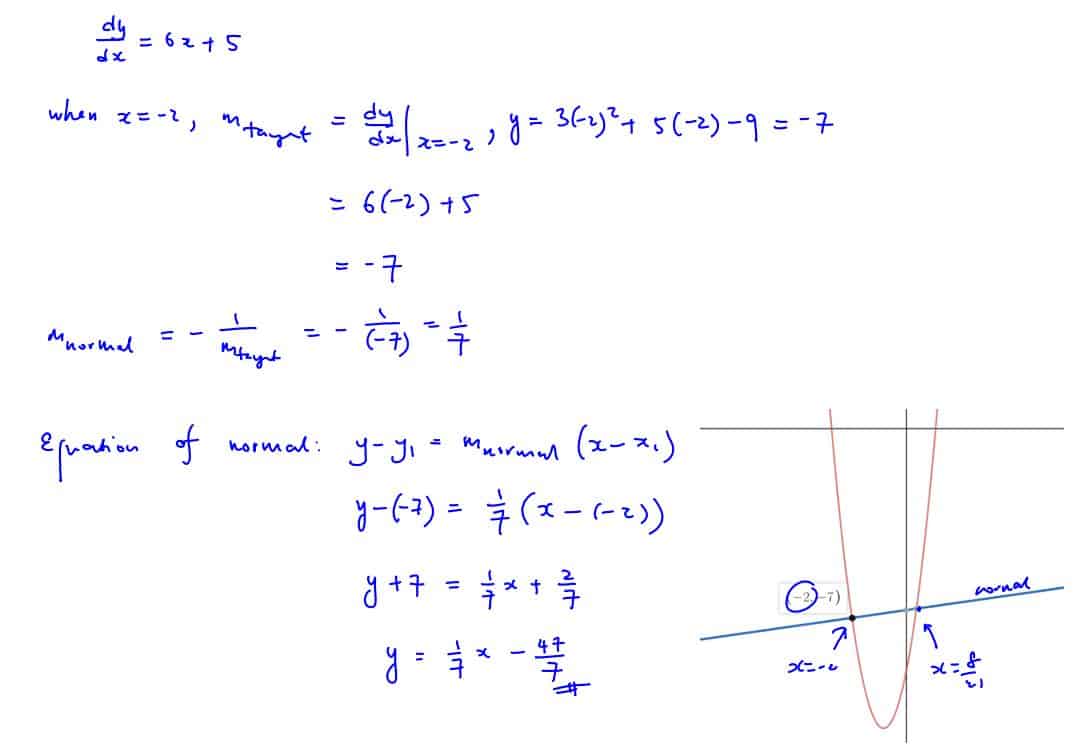
Practice Question 7
Meeting the Curve Again
Find the equation of the normal to the curve $y=3{{x}^{2}}+5x-9$ at the point where$x=-2$, hence find the $y$ -coordinate of the point where this normal meets the curve again.
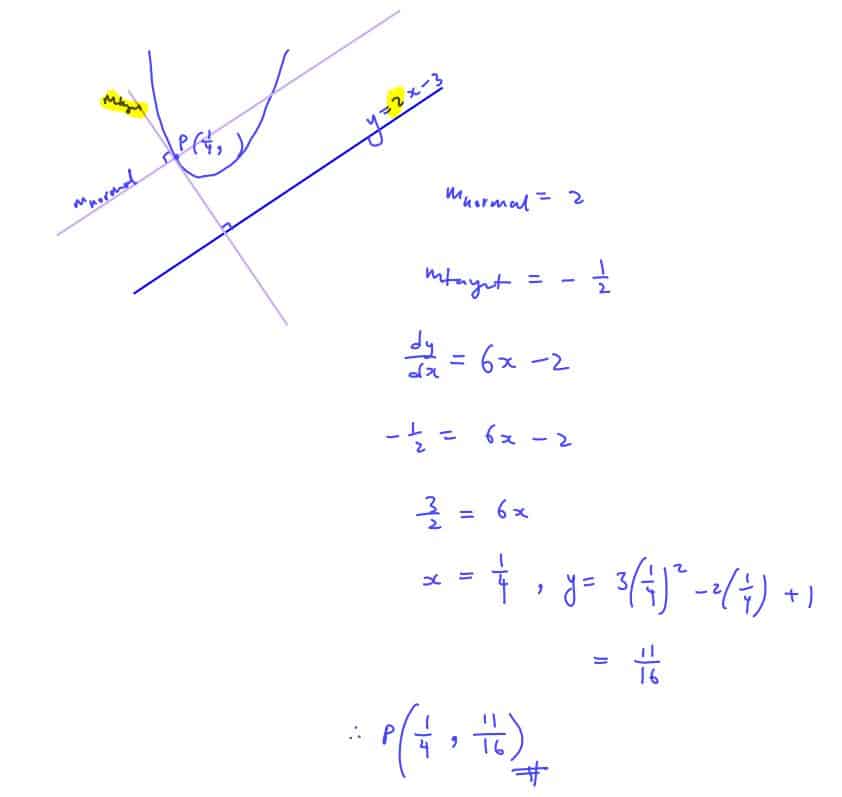
Practice Question 8
Finding Perpendicular and Parallel Lines
Find the coordinates of point $P$ on the curve $y=3{{x}^{2}}-2x+1$ for which the normal at $P$ is parallel to the line $y=2x-3$.
Connected Rate of Changes
In finding the derivative of a function, we have to know the rate at which the function is changing at each point. We can determine the rate of change of one thing with respect to another by taking the derivative of one variable with respect to the other. For example, if an object is moving in a straight line, the rate of change of its position with respect to time is called velocity and is defined as the measure of how quickly an object’s position changes over time. If two objects are moving at constant speeds along parallel lines, they are said to have constant relative velocity. If their speeds are different, they have a relative velocity that is different from this value. The rate of change of their relative velocity is called acceleration, which is defined as the derivative of their relative velocity with respect to time.
The same idea can be applied in different settings. Suppose we are doing investment in a fund that pays $3\%$ per annum, compounded annually, what would the amount in the account be after ten years if the starting amount is $\$1000$? We can calculate the rate of change of the amount in the account by using differentiation too. When you know how things change with respect to time, you know how they vary over different intervals of time. This allows you to predict how they will behave in the future and whether or not a problem can be solved.
The formula for connected rate of changes:
$\frac{\text{d}y}{\text{d}t}=\frac{\text{d}y}{{}}\times \frac{{}}{\text{d}t}$
Practice Question 9
The radius, $r$ cm, of a hemisphere is increasing at a constant rate of $0.5$ cm/s. Find the rate of increase of the volume of the hemisphere when $r=3$.
Practice Question 10
Connected Rate of Change involving Coordinate Geometry
The values of $x$ and $y$ are related by the equation $xy=23x-8$. If $x$ increases at the rate of $0.03$ unit/s, find the rate of change of $y$ when $y=21$.
Practice Question 11
Connected Rate of Change involving Area
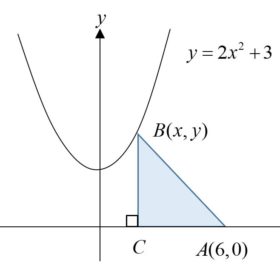
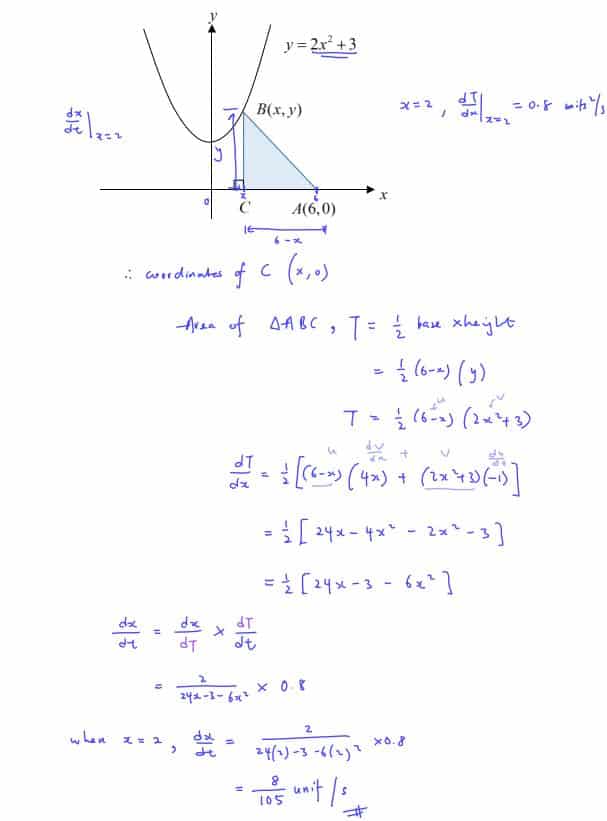
The figure shows part of the curve$y=2{{x}^{2}}+3$ . The point $B(x,y)$ is a variable point that moves along the curve for $0<x<6$ . $C$ is a point on the $x$-axis such that $BC$ is parallel to the $y$-axis and $A(6,0)$ lies on the $x$-axis. Express the area of triangle $ABC$, $T$ units², in terms of $x$, and find an expression for $\frac{\text{d}T}{\text{d}x}$. Given that when$x=2$, $T$ is increasing at the rate of $0.8$ units²/s, find the corresponding rate of change of $x$ at this instant.
Differentiation Strategies In Math
Increasing and Decreasing Functions
A function describes a relationship between two variables. The derivative of a function provides a lot of details to the shape of the graph; it is equal to the slope of the line tangent to the curve at that point. A positive derivative indicates an increasing function, a function where the value of its derivative is always positive; this means that if you plot its graph, you will see that the graph goes up as $x$ increases. Whereas a negative derivative indicates a decreasing one, with the value of its derivative being always negative; this means that if you plot its graph, you will see that the graph goes down as $x$ increases.
Practice Question 12
The equation of a curve is $y={{x}^{3}}+4{{x}^{2}}+kx+3$, where $k$ is a constant. Find the set of values of $k$ for which the curve is always an increasing function.
Stationary Points
What happens when the derivative is $0$? These points are called “stationary” because at these points the function is neither increasing nor decreasing. There are three types of stationary points: maximums, minimums, and points of inflexion.
The maximum and minimum are the largest and smallest values the function can take. The maximum is the highest point on the function’s graph. The minimum is the lowest point on the function’s graph. The point of inflexion is where the curve changes direction from increasing to decreasing, or from decreasing to increasing.
Take Note:
- Maximum and minimum points are also called turning points.
- All turning points are stationary points but not all stationary points are turning points.
- The stationary point of inflexion is a stationary point but not a turning point.
- Not all point of inflexion is a stationary point.
First Derivative Test
This is a technique used to find whether a given point is a maximum, minimum, or point of inflexion of a function. By determining whether the function is increasing or decreasing at these points, the approximate shape of the graph is obtained.
First Derivative Test
This is a technique used to find whether a given point is a maximum, minimum, or point of inflexion of a function. By determining whether the function is increasing or decreasing at these points, the approximate shape of the graph is obtained.
Practice Question 13
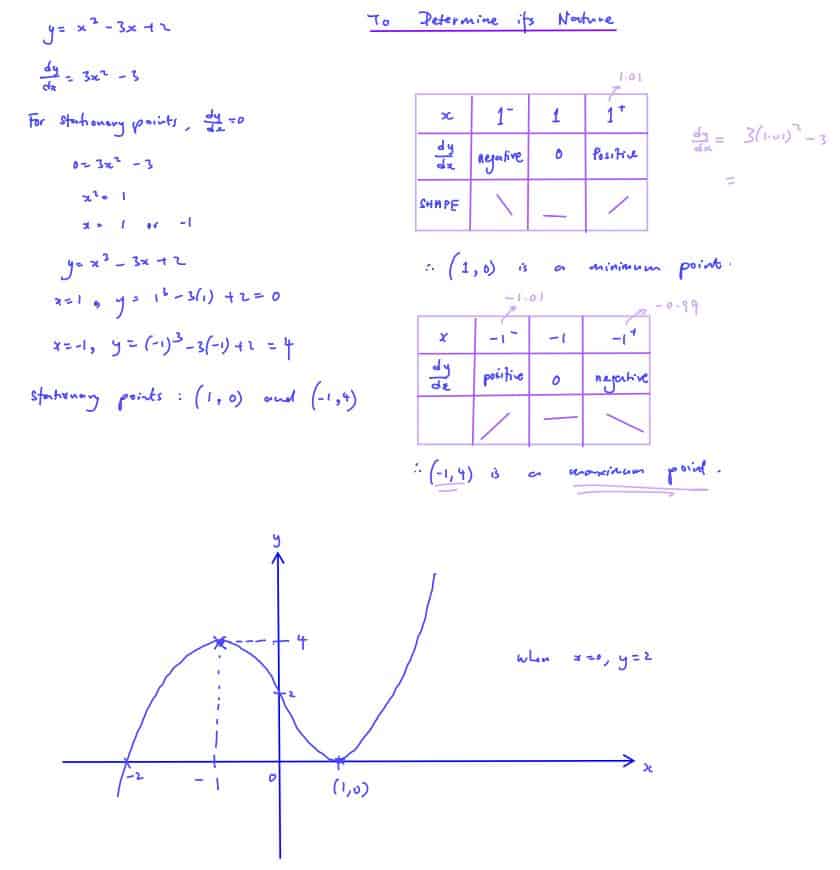
Find the coordinates of the stationary points on the curve $y={{x}^{3}}-3x+2$. Determine its nature by using the first derivative test. Hence, sketch the curve.
Second Derivative Test
The second derivative test is used to test the concavity of a function. It is a simple but powerful technique used to distinguish between a maximum point or minimum point. If the second derivative is negative, then it is a maximum point. If the second derivative is positive, then it is a minimum point. If the second derivative is zero, then it is a point of inflexion.
Second Derivative Test
The second derivative test is used to test the concavity of a function. It is a simple but powerful technique used to distinguish between a maximum point or minimum point. If the second derivative is negative, then it is a maximum point. If the second derivative is positive, then it is a minimum point. If the second derivative is zero, then it is a point of inflexion.
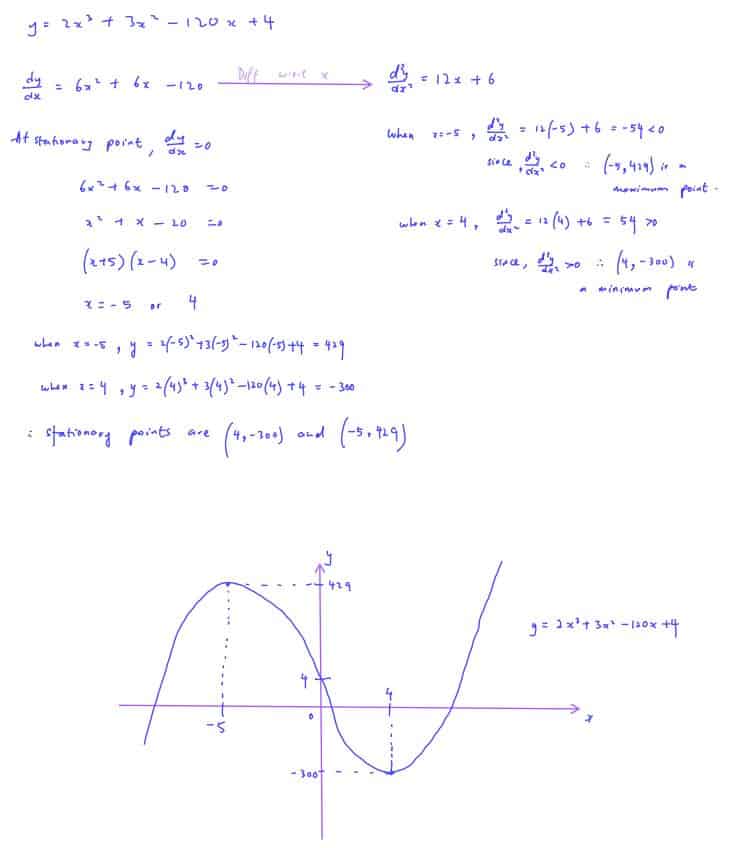
Practice Question 14
Find the coordinates of the stationary point on the curve $y=2{{x}^{3}}+3{{x}^{2}}-120x+4$. Determine its nature by using the second derivative test. Hence, sketch the curve.
$\leftarrow$ Here are some essential steps on solving problems involving maximum and minimum values.
Differentiation of Trigonometric, Logarithmic, And Exponential Functions
Basics of Trigonometric Derivative
Let’s have a look at the differentiation formula of trigonometric functions. You will have to use Chain Rule.
$\frac{\text{d}}{\text{d}x}(\cos (ax))=-a\sin \left( ax \right)$
$\frac{\text{d}}{\text{d}x}(\tan(ax))=a{{\sec }^{2}}\left( ax \right)$
$\frac{\text{d}}{\text{d}x}(\sin (ax))=a\cos \left( ax \right)$
Basics of Logarithmic Derivative
Logarithmic functions, have the following differentiation formulas:
$\frac{\text{d}}{\text{d}x}\left[ \ln x \right]=\frac{1}{x}$
$\frac{\text{d}}{\text{d}x}\left[ \ln \left( ax+b \right) \right]=\frac{a}{ax+b}$
Basics of Logarithmic Derivative
Logarithmic functions, have the following differentiation formulas:
$\frac{\text{d}}{\text{d}x}\left[ \ln x \right]=\frac{1}{x}$
$\frac{\text{d}}{\text{d}x}\left[ \ln \left( ax+b \right) \right]=\frac{a}{ax+b}$
Basics of Exponential Derivative
What about the differentiation formula for exponential functions?
$\frac{\text{d}}{\text{d}x}\left( {{e}^{x}} \right)={{e}^{x}}$
$\frac{\text{d}}{\text{d}x}\left( {{e}^{ax}} \right)=a{{e}^{ax}}$
Please note that there is an interesting case where $\frac{\text{d}}{\text{d}x}\left( {{e}^{x}} \right)={{e}^{x}}$. This is because the gradient is equal to the function itself.
Do sign up for our Free Mini-Courses and try our well-structured curriculum to see how it can help to maximize your learning in mathematics online.
Secondary School Additional Mathematics Free Online Course Sign Up.
You may also find the pricing and plans for our Additional Mathematics unlimited all-access courses here!
Topic List
Free Mini Course
With our online courses, you can learn at your own pace and take your time whenever it’s most convenient for you. Experience learning with us now for free!
Topics included:
- Derivative as a Gradient Function
- Chain Rule
- Problems involving Tangents and Normals
- Connected Rate of Change Involving Area