A-Level H2 Math | 5 Essential Questions
Arithmetic and Geometric Progressions
An ordered collection of numbers, also known as terms, when arranged in a specific order form sequence. The two types of sequences in mathematics are: arithmetic and geometric progressions. The sequence of numbers where the difference between each consecutive term is constant is called arithmetic progression. Meanwhile, geometric progression consists of a sequence of numbers where the consecutive terms differ by a constant ratio.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2009 VJC J1 MYE Q10
The terms of a geometric progression ${{u}_{1}},{{u}_{2}},{{u}_{3}},{{u}_{4}},…$ are such that the sum to infinity is $81$ and the sum of the first $4$ terms is $80$.
If ${{u}_{1}}>100\,\,$and $\,\text{n}\ge \text{3}$,
(i)
find ${{u}_{n}}$ in terms of $n$,
[5]
(i) find ${{u}_{n}}$ in terms of $n$,
[5]
(ii)
show that ${{u}_{3}}+{{u}_{4}}+{{u}_{5}}+…+{{u}_{n}}=\,p\left[ 1-{{\left( -\frac{1}{3} \right)}^{n+q}} \right]$, where the integers $p$ and $q$ are to be found.
[3]
(ii) show that ${{u}_{3}}+{{u}_{4}}+{{u}_{5}}+…+{{u}_{n}}=\,p\left[ 1-{{\left( -\frac{1}{3} \right)}^{n+q}} \right]$, where the integers $p$ and $q$ are to be found.
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
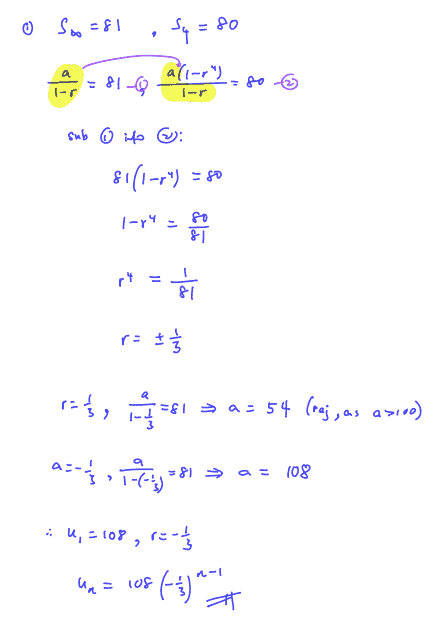
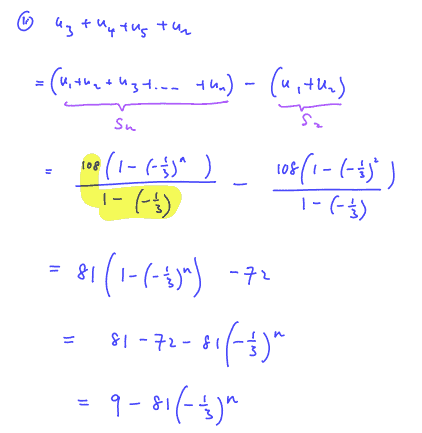
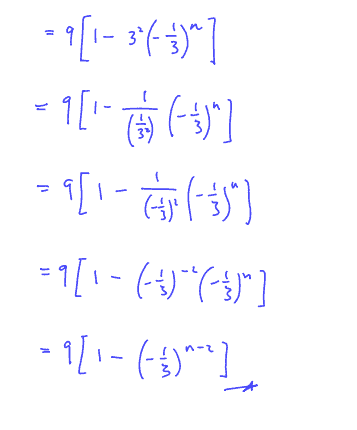
- (i)
- (ii)
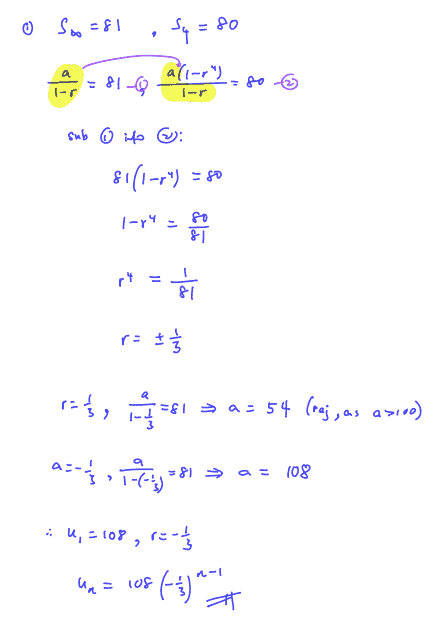
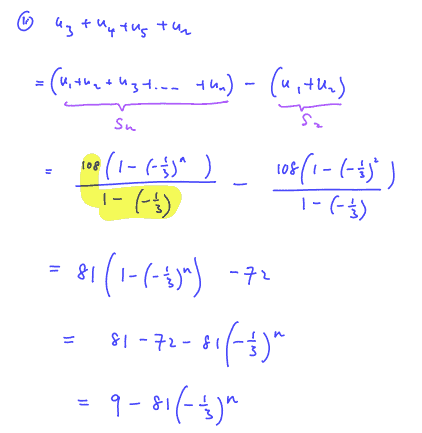
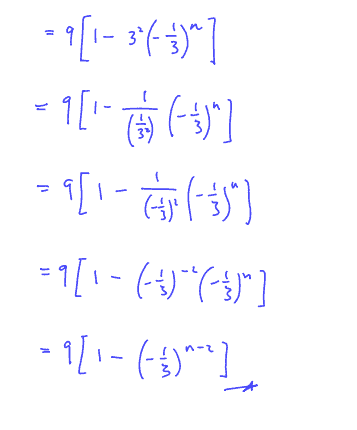
Share with your friends!
2020 RI P2 Q1
An arithmetic series has first term $\frac{3}{2}$ and fourth term ${{u}_{4}}$.
A geometric series also has first term $\frac{3}{2}$ and fourth term ${{u}_{4}}$.
Given that the common ratio of the geometric series is non-negative and the sum of its first $3$ terms is $\frac{21}{2}$, find the sum of the first $10$ odd-numbered terms of the arithmetic series.
[5]
Suggested Handwritten and Video Solutions
Share with your friends!
2017 TJC P1 Q5
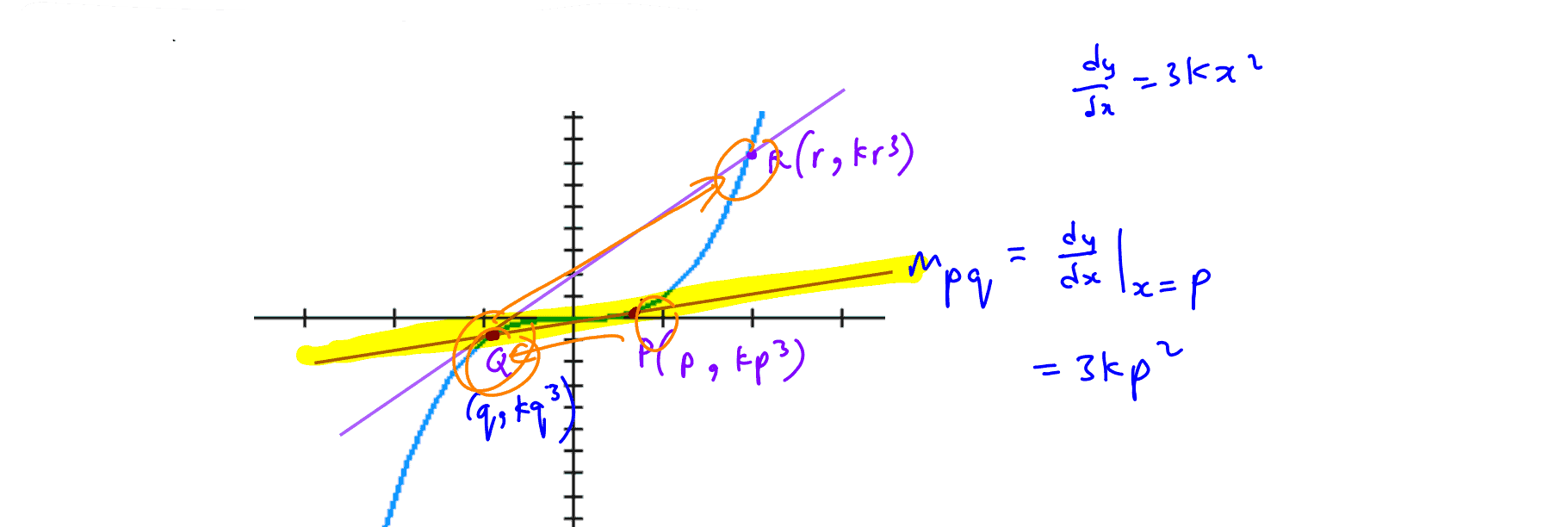
The curve $C$ has equation $y=k{{x}^{3}}$ . The tangent at the point $P$ on $C$ meets the curve again at point $Q$. The tangent at point $Q$ meets the curve again at point $R$. If the $x$ coordinates of $P$, $Q$ and $R$ are $p$ , $q$, and $r$ respectively where $p\ne 0$ .
(i)
Show that $p$ and $q$ satisfy the equation ${{\left( \frac{q}{p} \right)}^{2}}+\left( \frac{q}{p} \right)-2=0$ .
[4]
(i) Show that $p$ and $q$ satisfy the equation ${{\left( \frac{q}{p} \right)}^{2}}+\left( \frac{q}{p} \right)-2=0$ .
[4]
(ii)
Show that $p$ , $q$, and $r$ are three consecutive terms of a geometric progression. Hence determine if this geometric series is convergent.
[4]
(ii) Show that $p$ , $q$, and $r$ are three consecutive terms of a geometric progression. Hence determine if this geometric series is convergent.
[4]
[You may use the identity ${{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)$ for $a,b\in \mathbb{R}$.]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
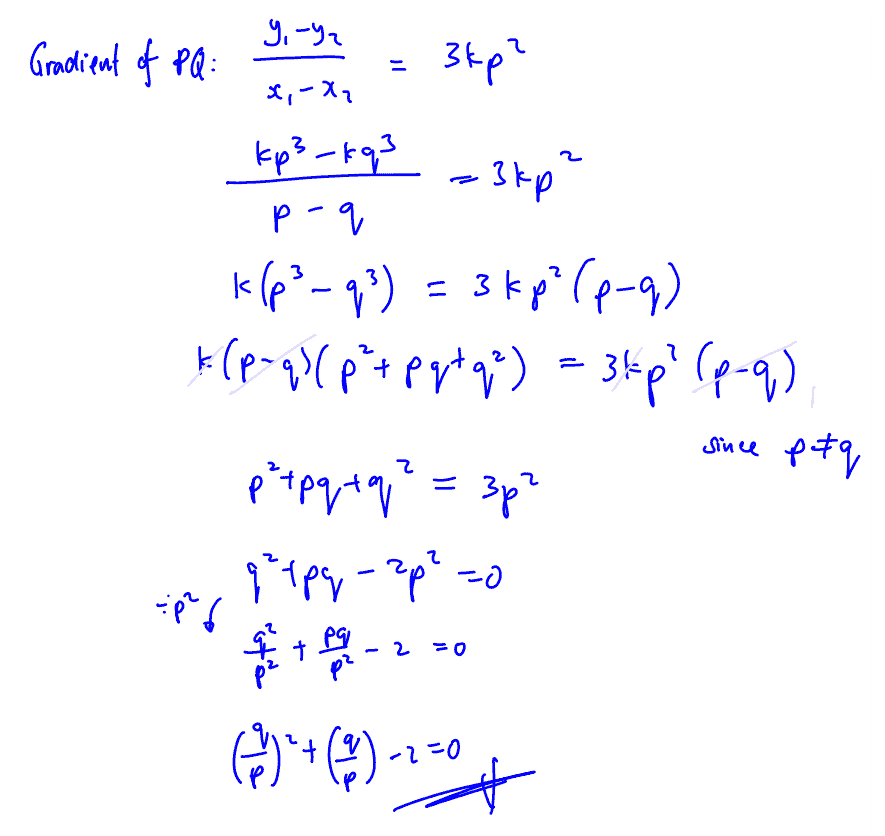
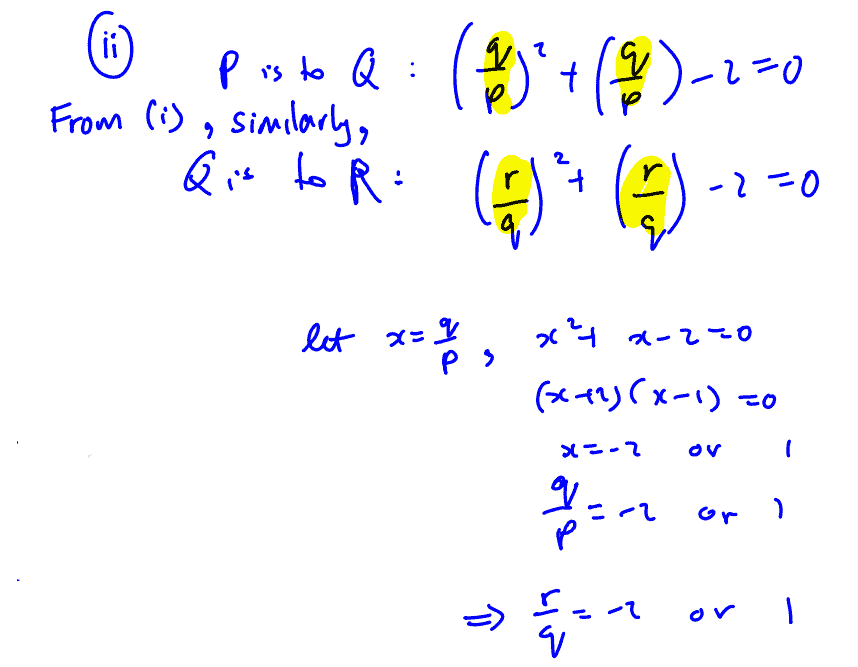

- (i)
- (ii)

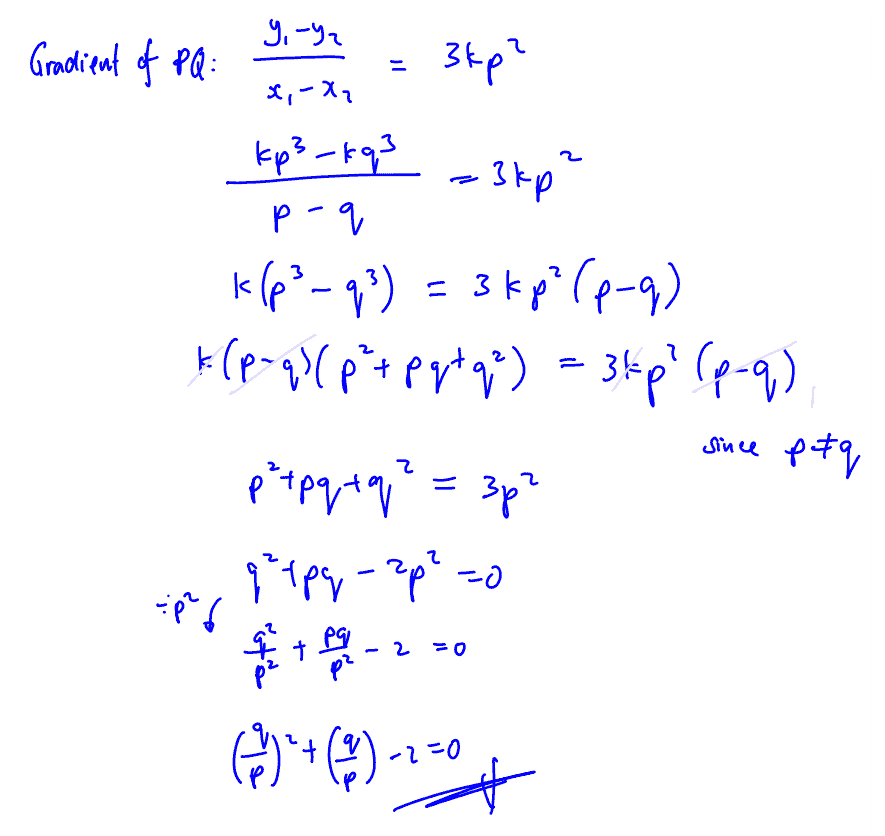
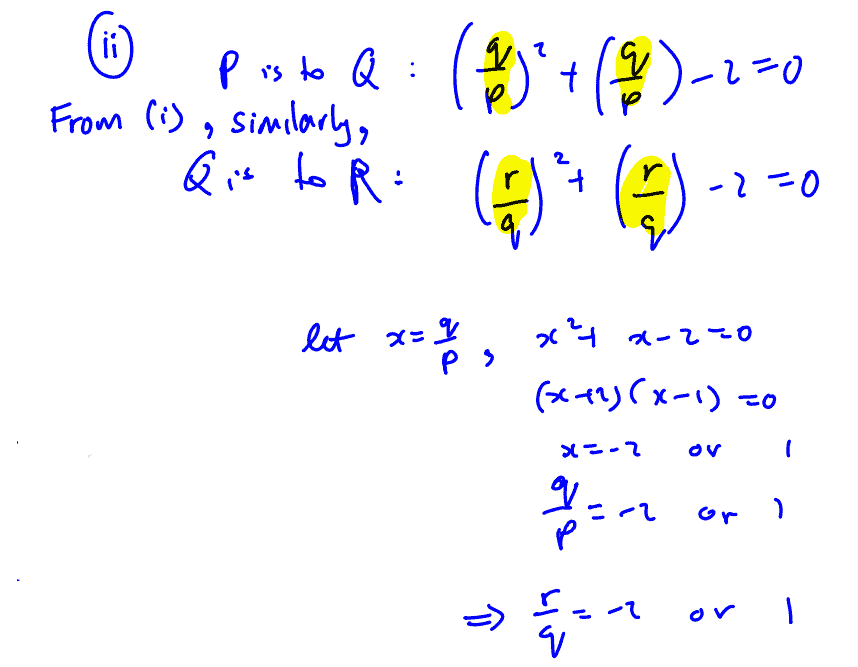

Share with your friends!
2017 JJC P1 Q4
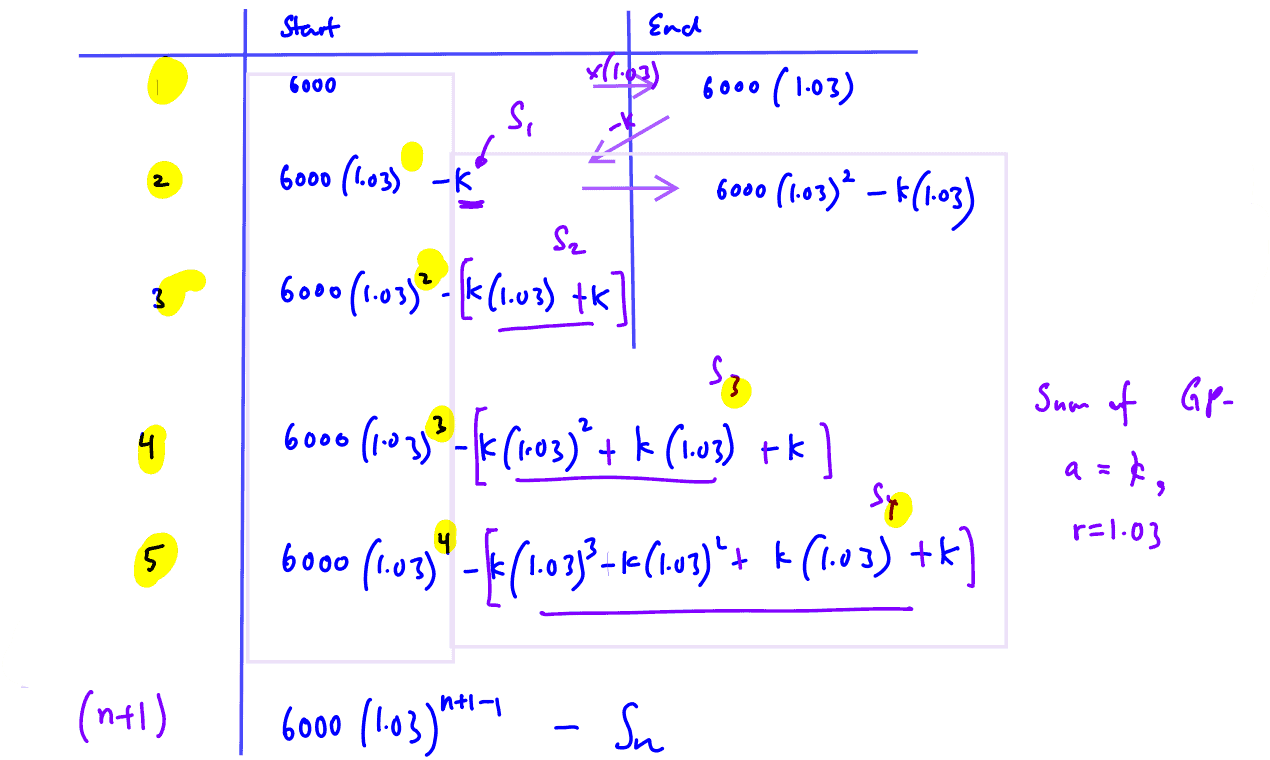
A fund is started at $\$6000$ and compound interest of $3\%$ is added to the fund at the end of each year. If withdrawals of $\$k$ are made at the beginning of each of the subsequent years, show that the amount in the fund at the beginning of the $\left( n+1 \right)$th year is
$\$\frac{100}{3}\left[\left(180-k\right){{\left(1.03\right)}^{n}}+k\right]$.
[5]
(i)
It is given that $k=400$. At the beginning of which year, for the first time, will the amount in the fund be less than $\$1000$?
[2]
(i) It is given that $k=400$. At the beginning of which year, for the first time, will the amount in the fund be less than $\$1000$?
[2]
(ii)
If the fund is fully withdrawn at the beginning of sixteenth year, find the least value of $k$ to the nearest integer.
[2]
(ii) If the fund is fully withdrawn at the beginning of sixteenth year, find the least value of $k$ to the nearest integer.
[2]
Suggested Handwritten and Video Solutions
- -
- (i)
- (ii)

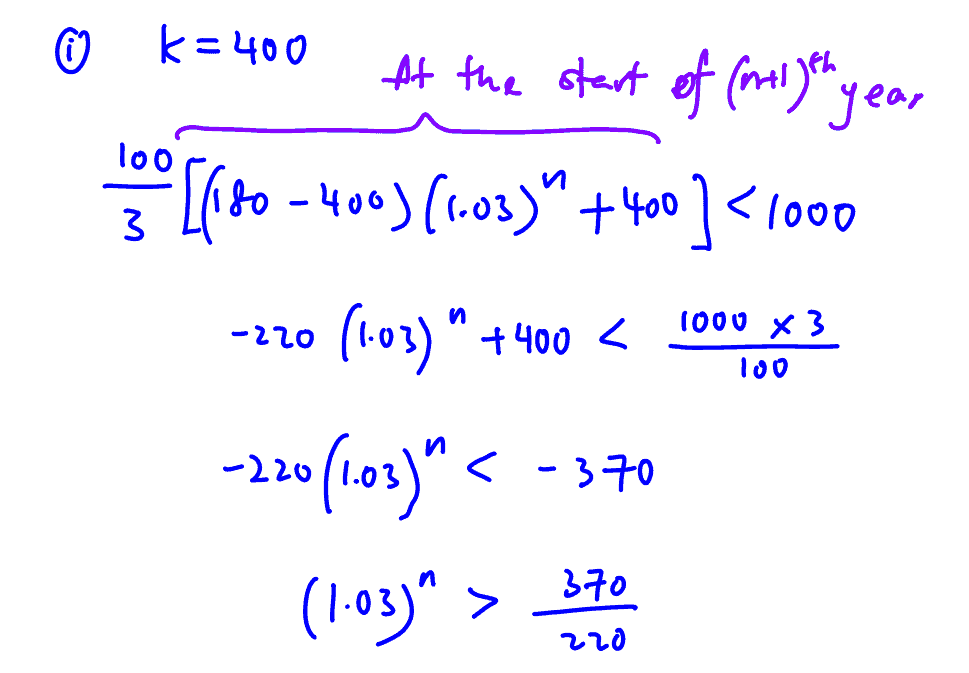
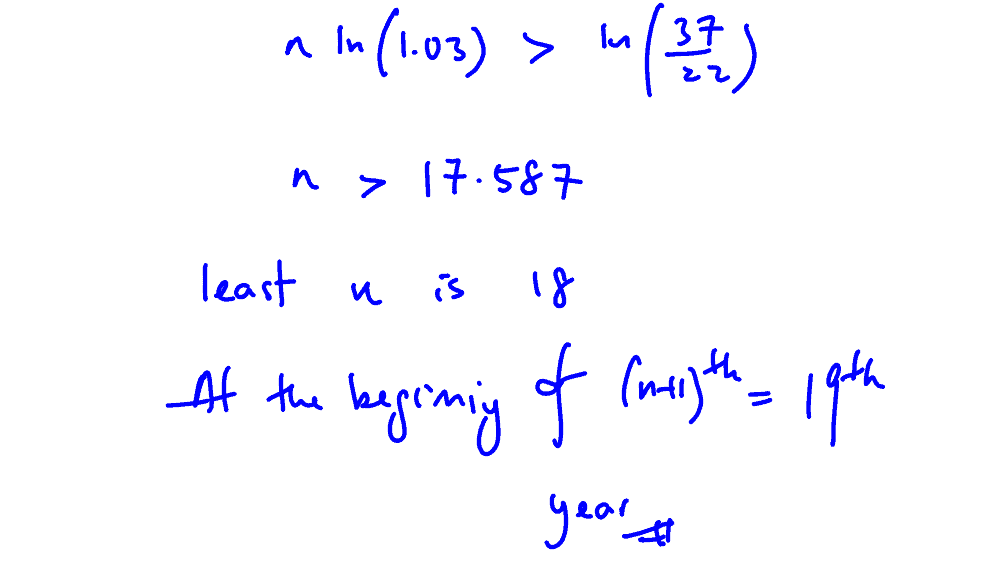
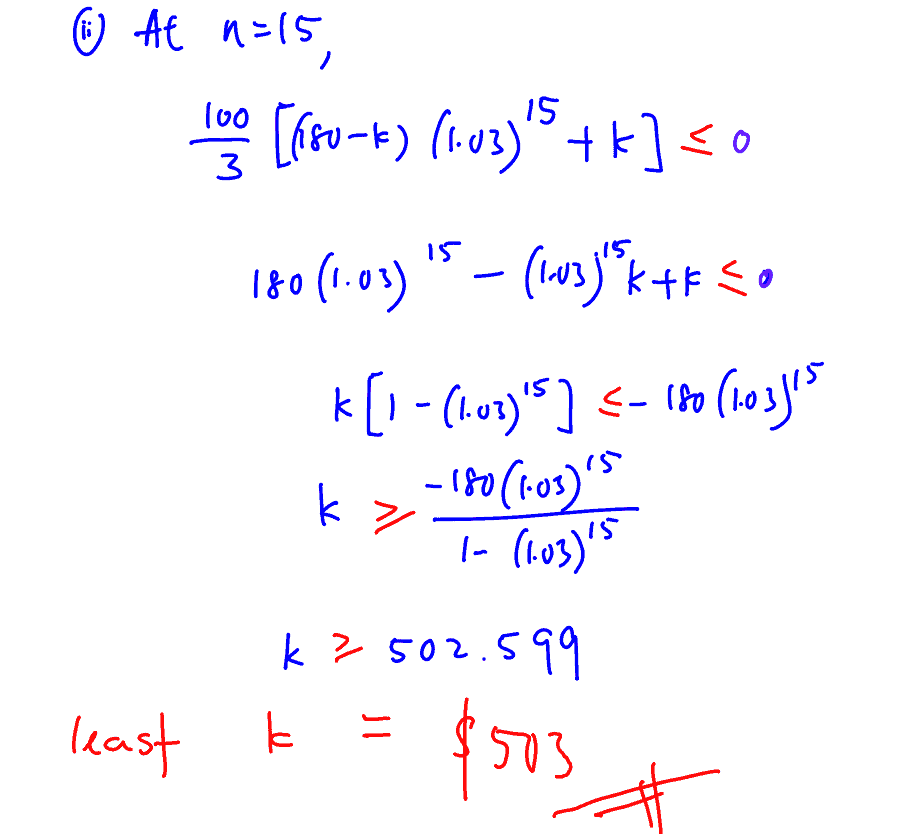
- -
- (i)
- (ii)


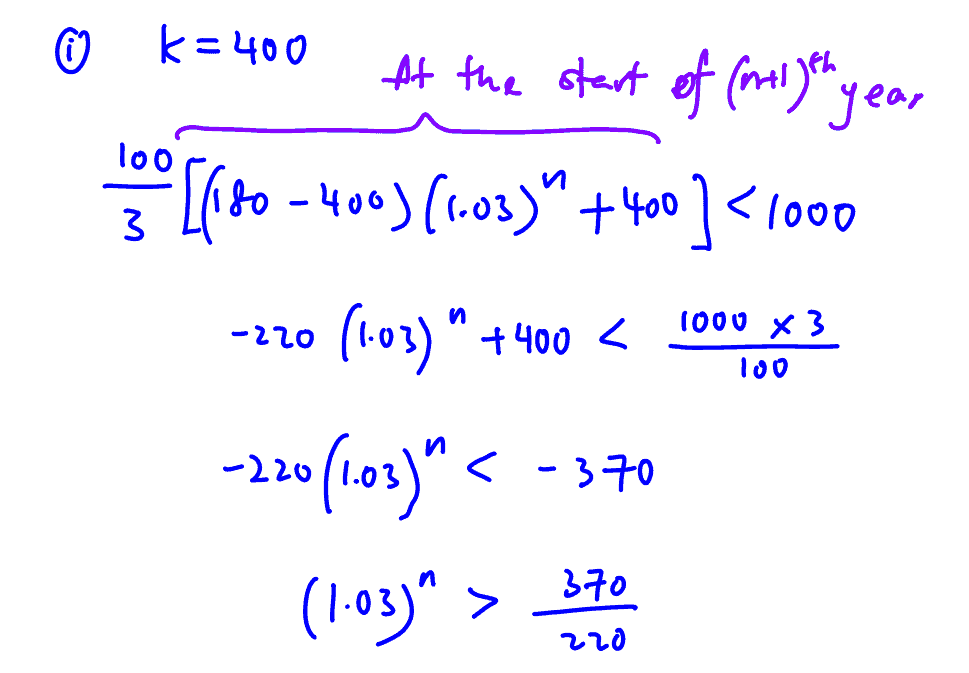
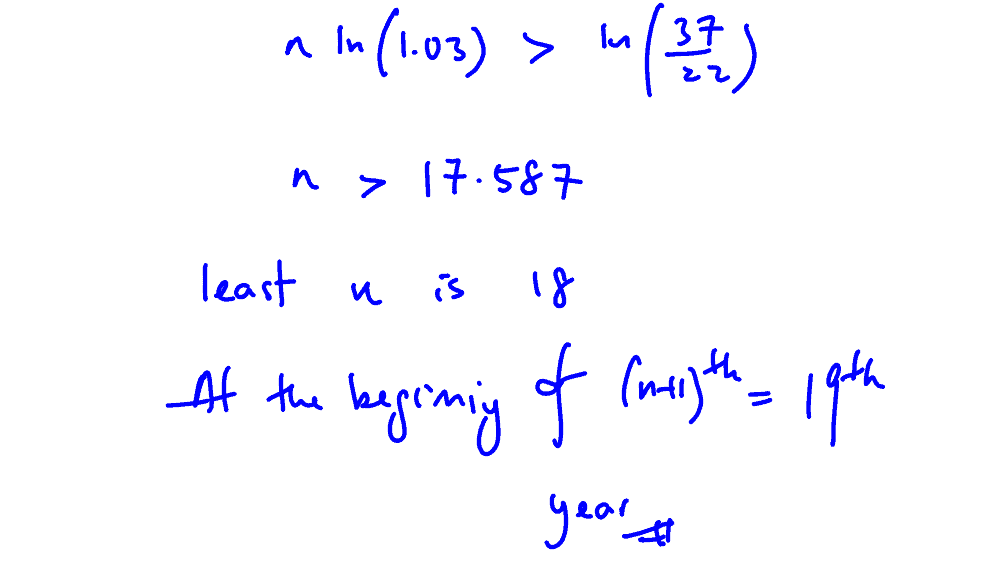
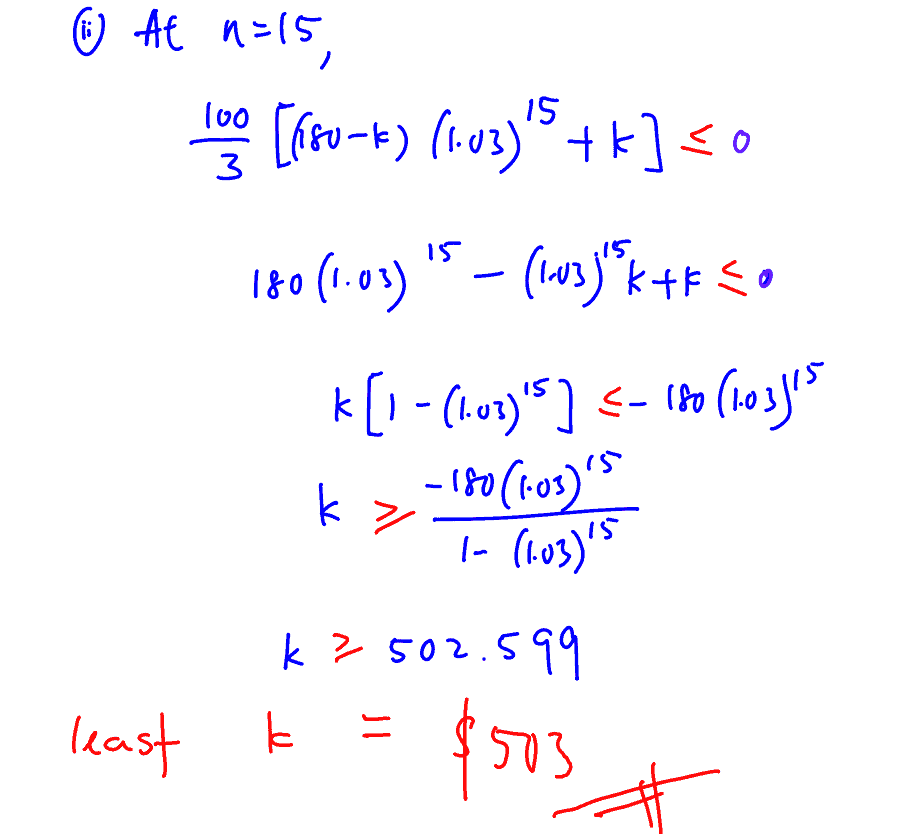
Share with your friends!
2021 HCI J1 CT1 Q5
Jane deposited \$ $x$ on 1 January $2018$ and then a further \$ $x$ on 1 February $2018$ and at the start of every subsequent month in a bank account. The interest rate was $0.3\%$ per month, so that on the last day of each month the amount in the account on that day was increased by $0.3\%$.
(i)
Find an expression in terms of $n$ and $x$ for the amount of money in the bank account on the last day of the $n$th month.
[3]
(i) Find an expression in terms of $n$ and $x$ for the amount of money in the bank account on the last day of the $n$th month.
[3]
(ii)
What is the minimum amount (to the nearest dollar) Jane should deposit in the bank every month if she were to have at least \$ $5000$ in the bank at the end of $15$ months?
[2]
(ii) What is the minimum amount (to the nearest dollar) Jane should deposit in the bank every month if she were to have at least \$ $5000$ in the bank at the end of $15$ months?
[2]
After $2$ years, Jane stopped depositing \$ $x$ per month, and instead decided to withdraw \$ $200$ from the account on the ${{15}^{\text{th}}}$ of every subsequent month, starting on ${{15}^{\text{th}}}$ January 2020. The interest rate remained as $0.3\%$ per month, so that on the last day of each month the amount in the account on that day was increased by $0.3\%$.
(iii)
Using the value of $x$ found in part (ii), find the date in which Jane would do her last withdrawal till she has no more money left in her account, and the amount of her last withdrawal to the nearest cent.
[5]
(iii) Using the value of $x$ found in part (ii), find the date in which Jane would do her last withdrawal till she has no more money left in her account, and the amount of her last withdrawal to the nearest cent.
[5]
Having no money left in her bank account, Jane decided to take an interest free loan of \$ $10\,000$ from a friend. She would repay her friend \$ $100$ on the last day of the first month she took the loan. On the last day of each subsequent month, she would repay her friend \$ $150$ more than the amount she repaid in the previous month.
(iv)
Find the number of months Jane will take to repay her loan.
[2]
(iv) Find the number of months Jane will take to repay her loan.
[2]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
- (iv)

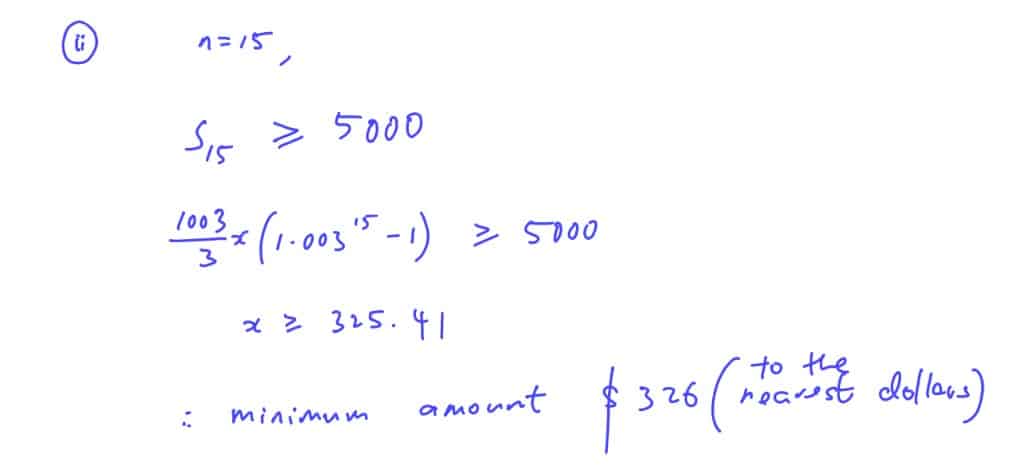



- (i)
- (ii)
- (iii)
- (iv)

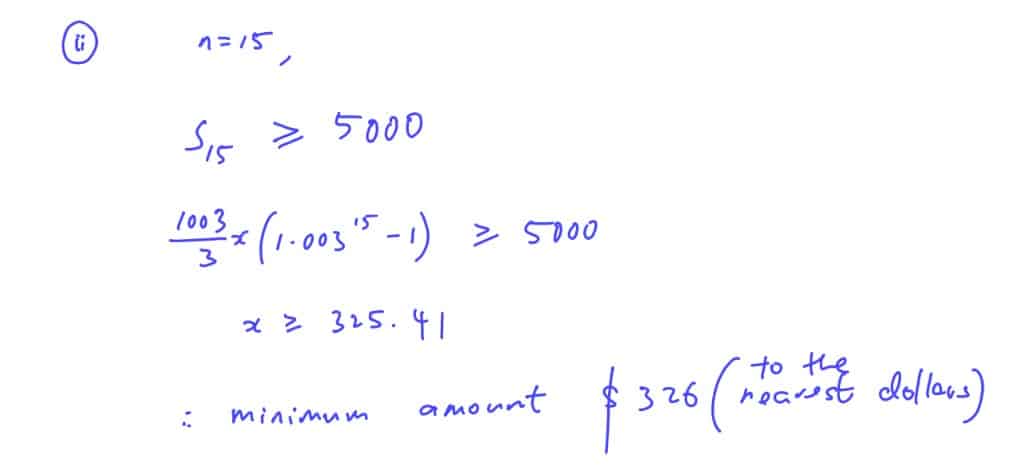



Share with your friends!
Download Arithmetic and Geometric Progressions Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!


