A-Level H2 Math | 5 Essential Questions
Maclaurin and Power Series
Maclaurin series refers to the expansion of a series of functions where the estimated value of the function is determined as a sum of the derivatives of that function when evaluated at zero. It is named after Colin Maclaurin (1698–1746), a Scottish mathematician who made extensive use of this special case of Taylor series in the 18th century.
Maclaurin series are very frequently used to approximate functions.
This free online revision course is specially designed for students to revise important topics from A Level H2 Maths. The course content is presented in an easy to study format with 5 essential questions, core concepts and explanation videos for each topic. Please download the worksheet and try the questions yourself! Have fun learning with us, consider joining our tuition classes or online courses.
- Q1
- Q2
- Q3
- Q4
- Q5
2009 HCI Promo P1 Q3 Modified
Expand $\frac{{{x}^{2}}+2x}{2{{x}^{2}}+1}$ in ascending powers of $x$ up to and including the term in ${{x}^{5}}$. State the range of values of $x$ for which this expansion is valid.
[3]
Find, in the simplest form, the coefficient of ${{x}^{2017}}$ in this expansion.
[2]
Suggested Handwritten and Video Solutions
- I
- II

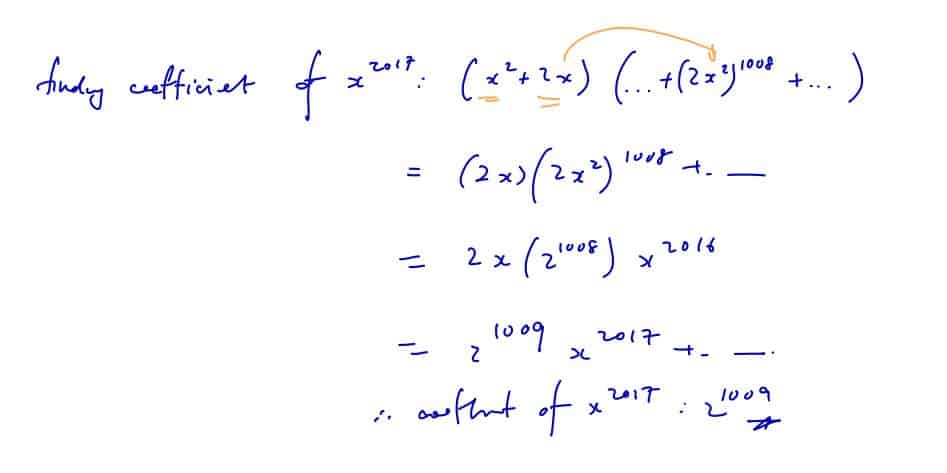
- I
- II

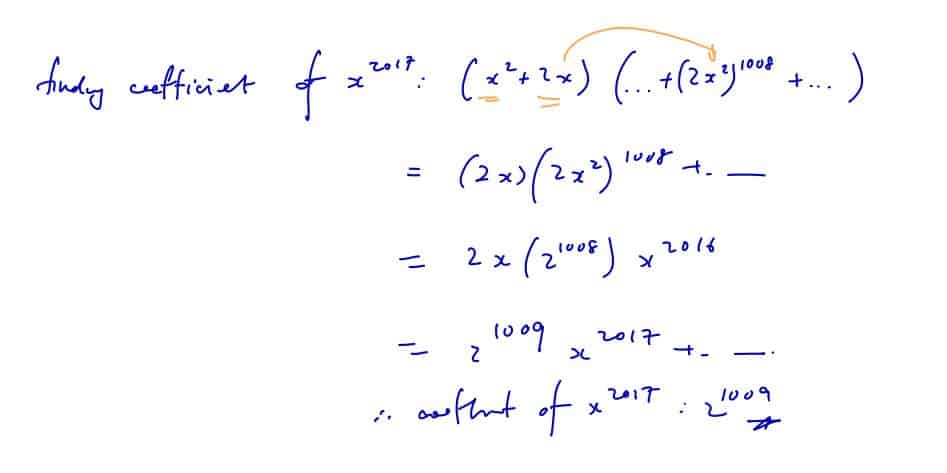
Share with your friends!
2020 MI P1 Q6
It is given that $y=\sqrt{{{\text{e}}^{x}}\cos x}$.
(i)
Show that $2y\frac{\text{d}y}{\text{d}x}={{y}^{2}}-{{\text{e}}^{x}}\sin x$.
[2]
(i) Show that $2y\frac{\text{d}y}{\text{d}x}={{y}^{2}}-{{\text{e}}^{x}}\sin x$.
[2]
(ii)
By further differentiation of the result in part (i), find the Maclaurin series for $y$, up to and including the term in ${{x}^{2}}$.
[4]
(ii) By further differentiation of the result in part (i), find the Maclaurin series for $y$, up to and including the term in ${{x}^{2}}$.
[4]
(iii)
Using the standard series from the List of Formulae (MF 26). Expand $\sqrt{{{\text{e}}^{x}}\cos x}$ as far as the term in ${{x}^{2}}$ and verify that the same result is obtained in part (ii).
[3]
(iii) Using the standard series from the List of Formulae (MF 26). Expand $\sqrt{{{\text{e}}^{x}}\cos x}$ as far as the term in ${{x}^{2}}$ and verify that the same result is obtained in part (ii).
[3]
Suggested Handwritten and Video Solutions
- (i)
- (ii)
- (iii)
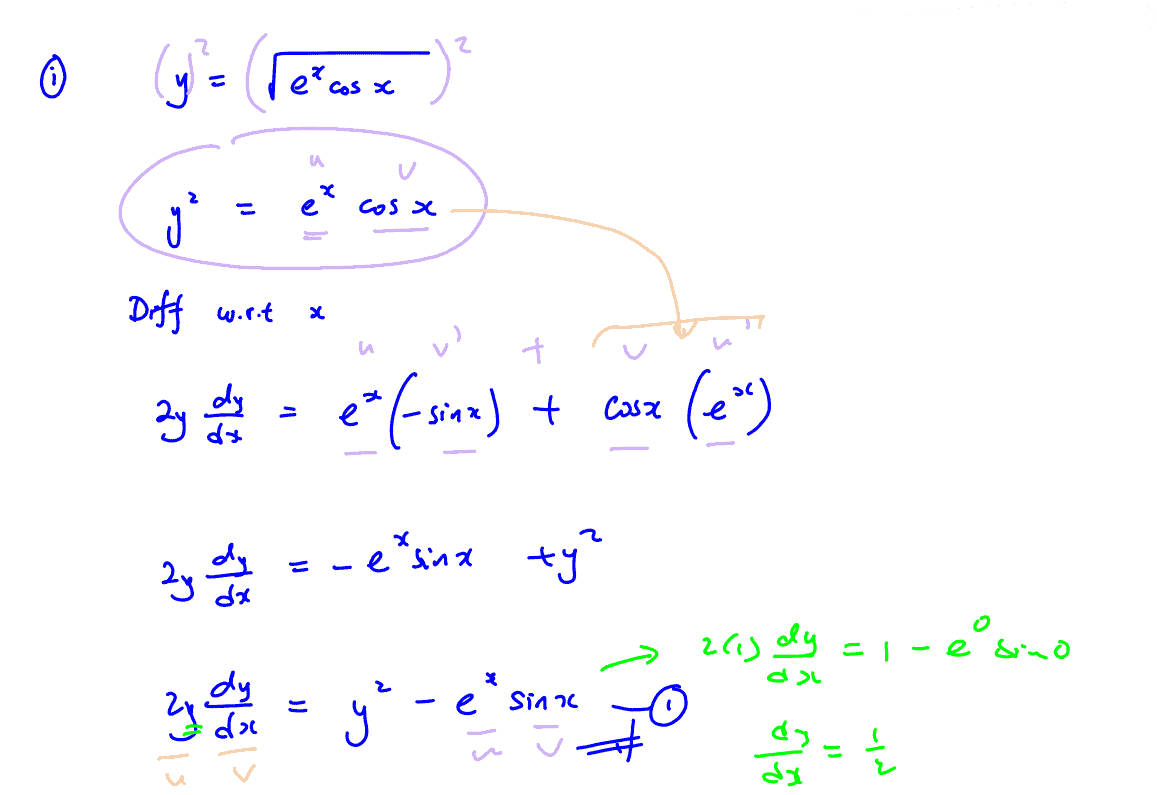
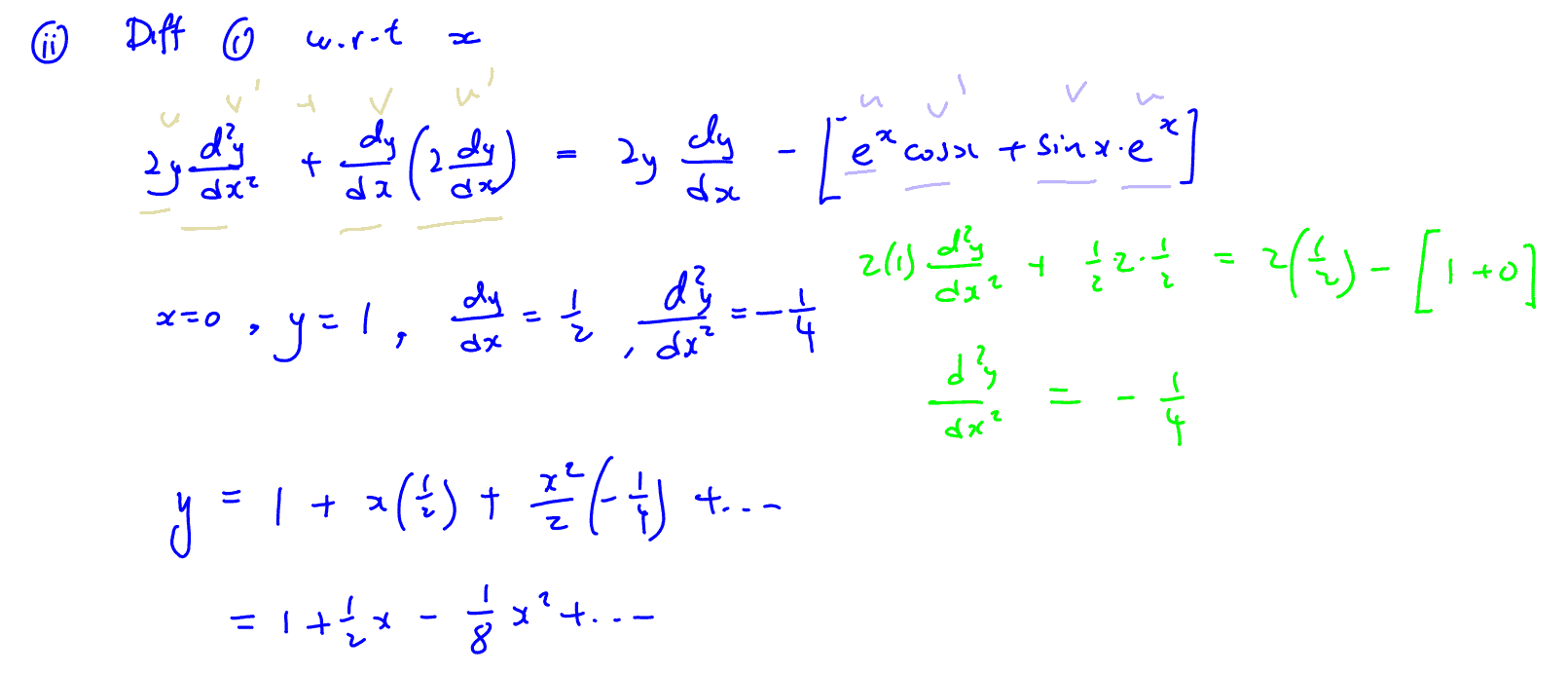
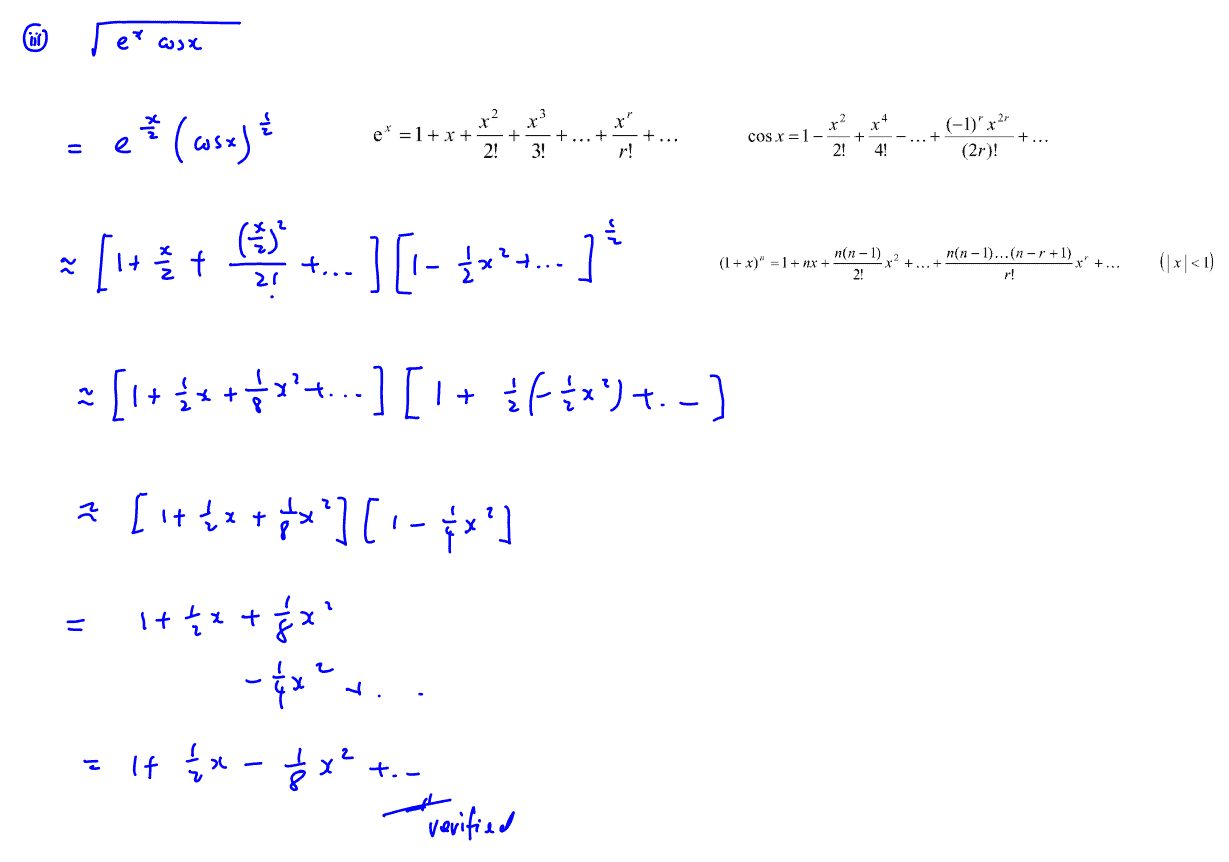
- (i)
- (ii)
- (iii)
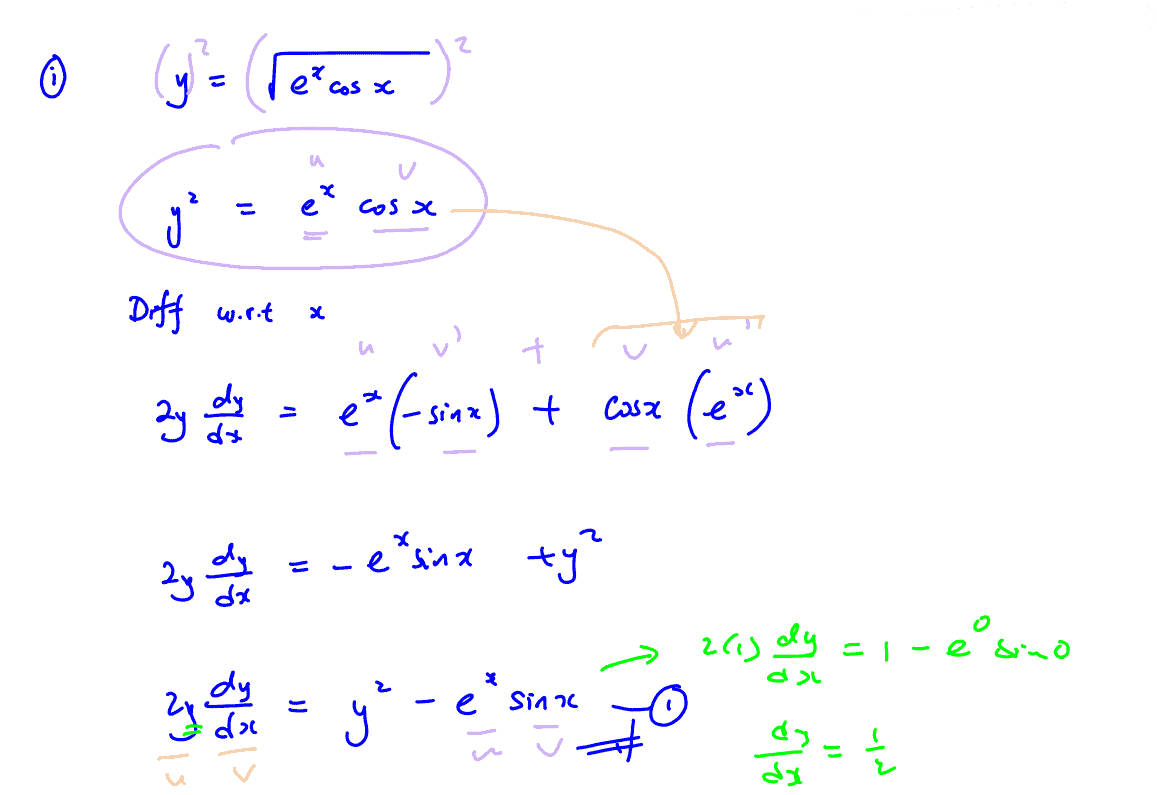
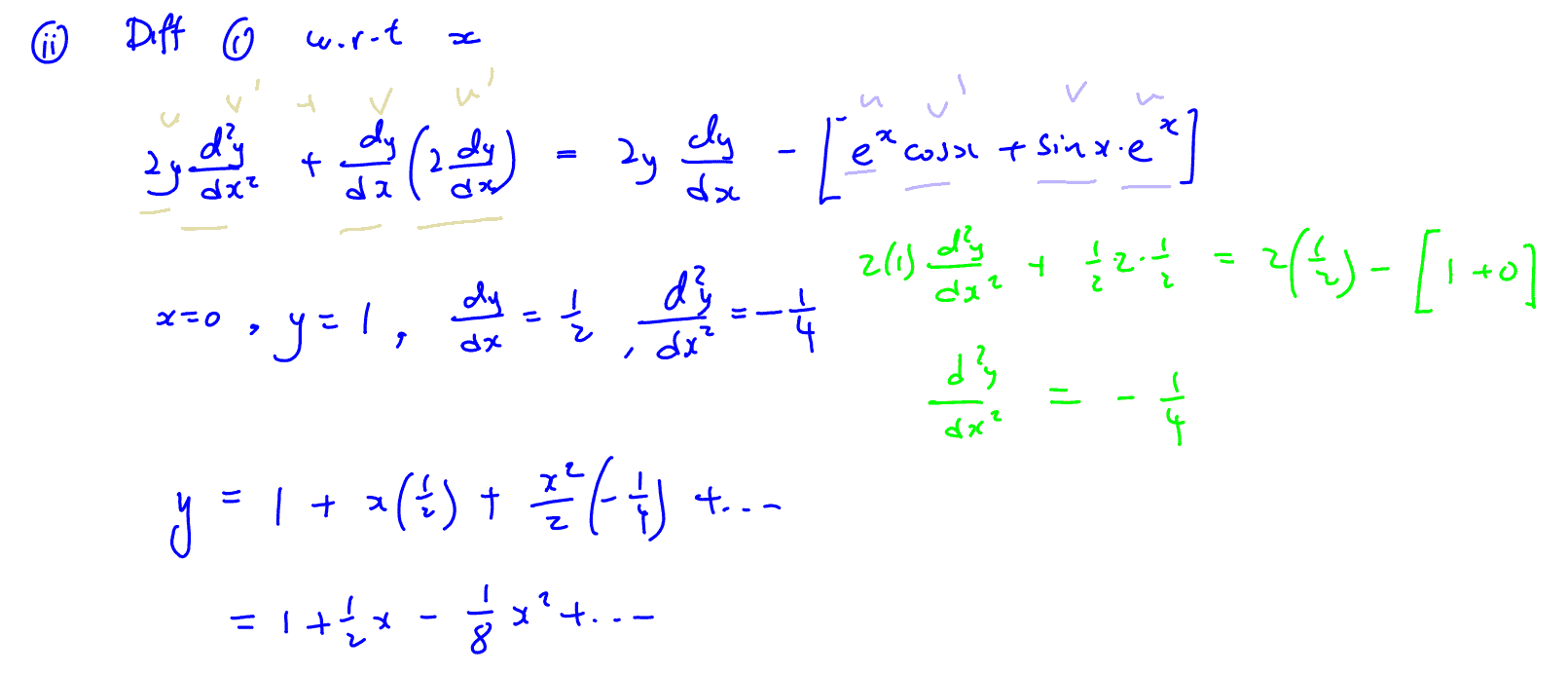
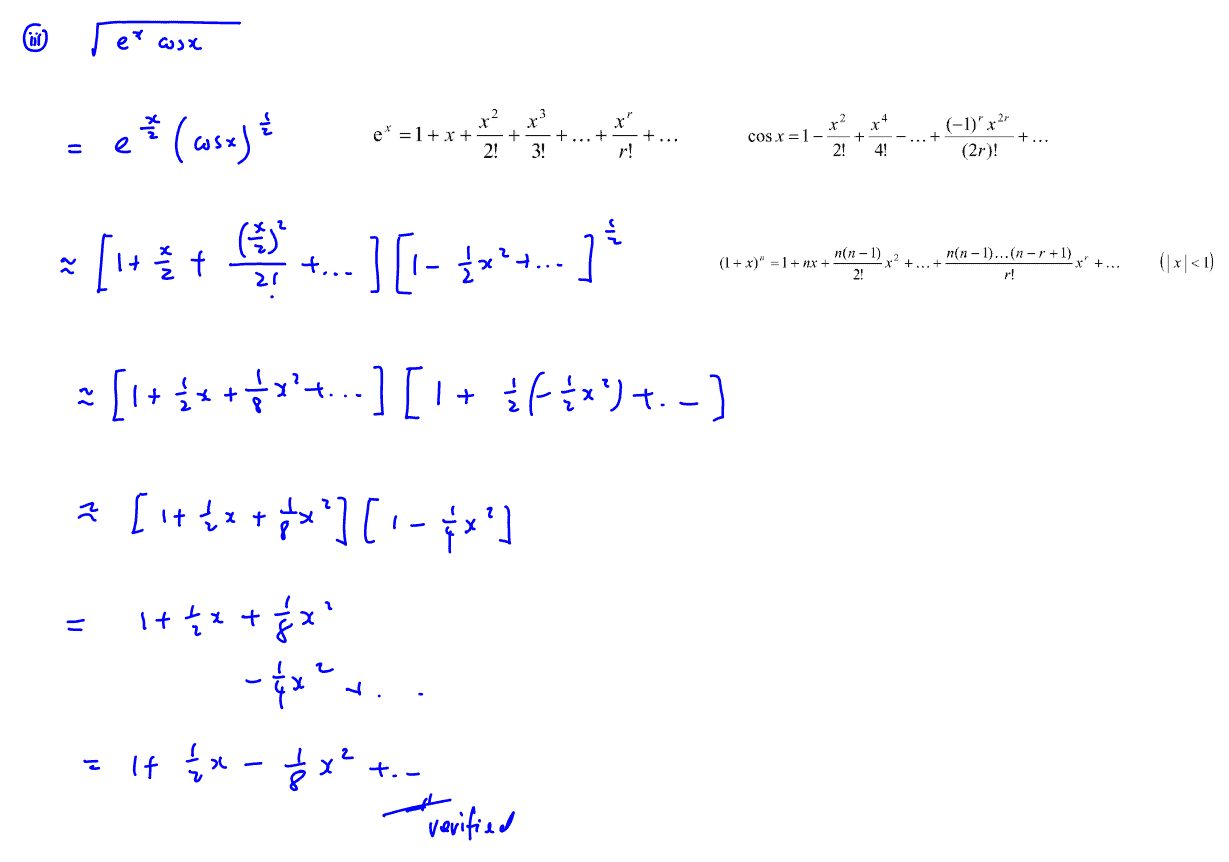
Share with your friends!
2013 ACJC P1 Q12
$\left( 1-{{x}^{2}} \right){{\left( \frac{\text{d}y}{\text{d}x} \right)}^{2}}=4y$
and $\left( 1-{{x}^{2}} \right)\frac{{{\text{d}}^{\text{2}}}y}{\text{d}{{x}^{2}}}-x\frac{\text{d}y}{\text{d}x}=2$.
[3]
By further differentiation of these results, find the Maclaurin series of $y$ up to including the term in ${{x}^{4}}$.
[3]
Suggested Handwritten and Video Solutions
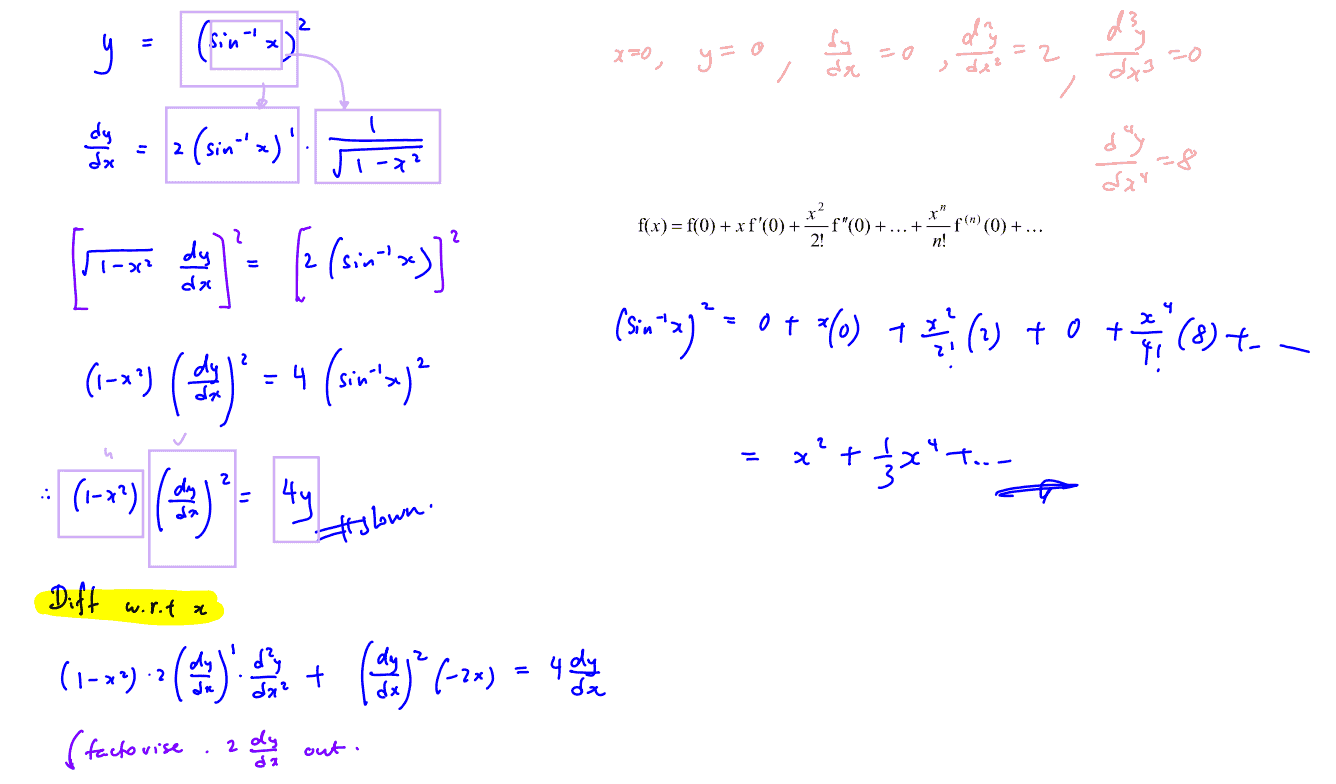
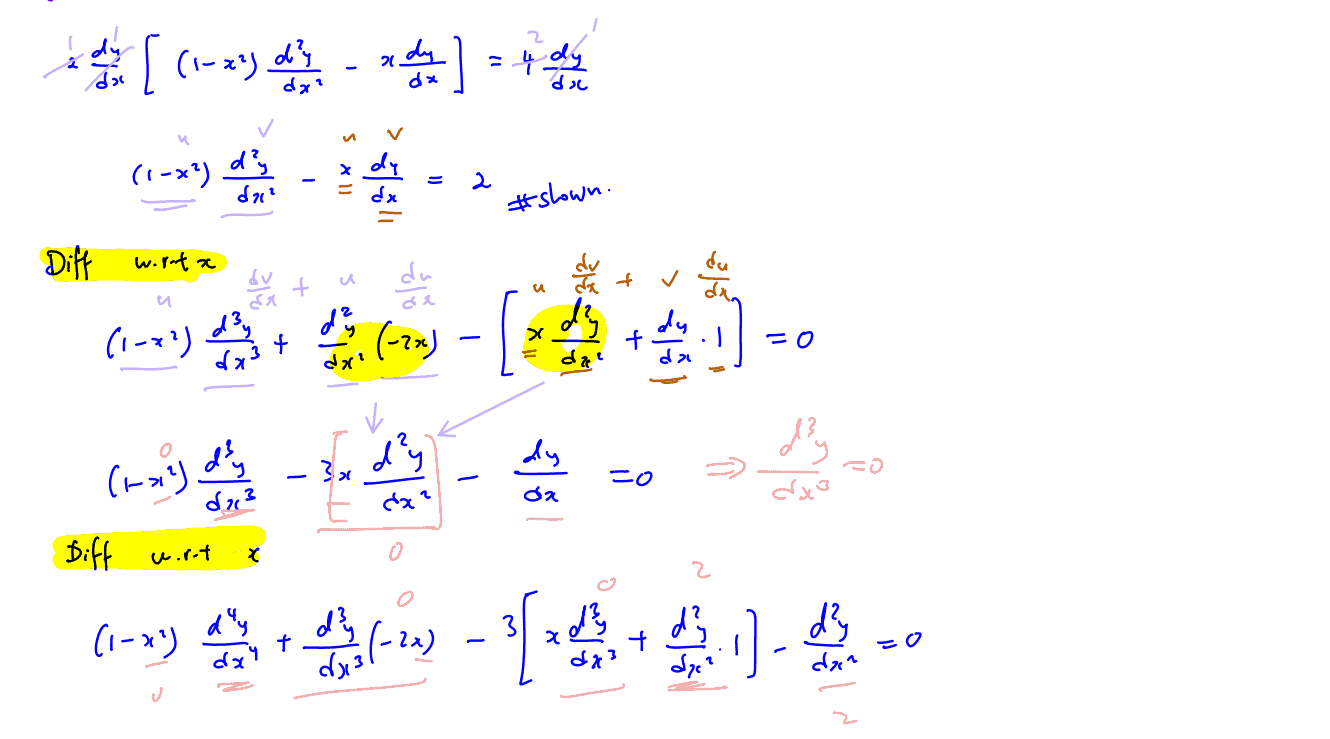
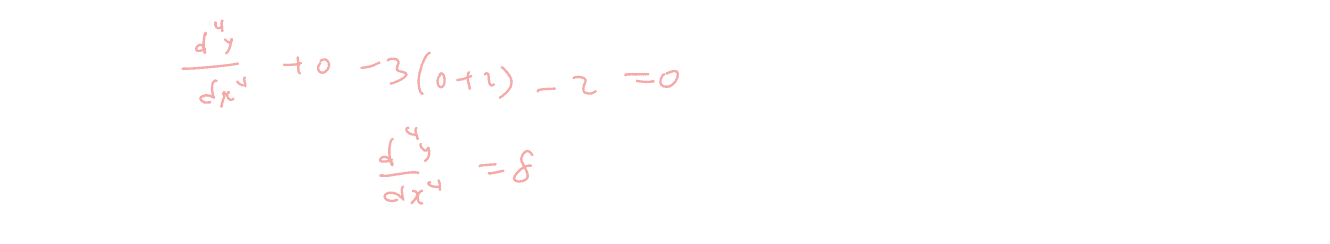
Share with your friends!
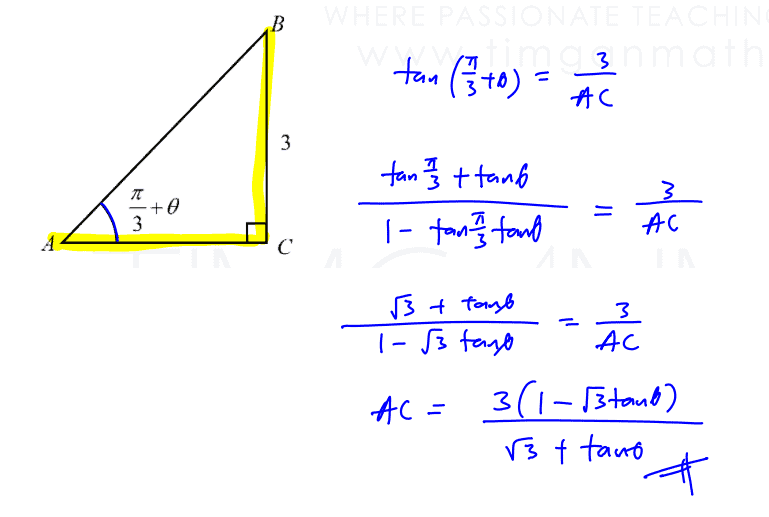
2017 PJC Promo Q9 (a)
In the triangle $ABC$ as shown below, $BC=3$, angle $BAC=\frac{\pi }{3}+\theta $ radians and angle $ACB=\frac{\pi }{2}$ radians.
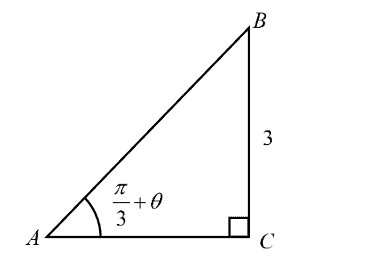 Show that $AC=\frac{3\left( 1-\sqrt{3}\tan \theta \right)}{\sqrt{3}+\tan \theta }$.
Show that $AC=\frac{3\left( 1-\sqrt{3}\tan \theta \right)}{\sqrt{3}+\tan \theta }$.
[3]
Given that $\theta $ is a sufficiently small angle, deduce that $AC\approx \sqrt{3}+a\theta $, where $a$ is a constant to be determined.[3]
Suggested Handwritten and Video Solutions
- I
- II
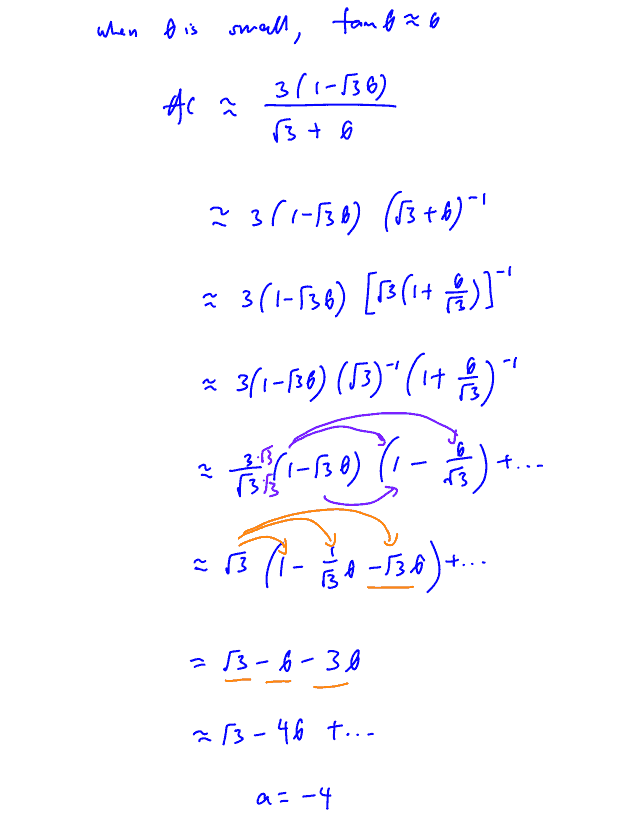
- I
- II

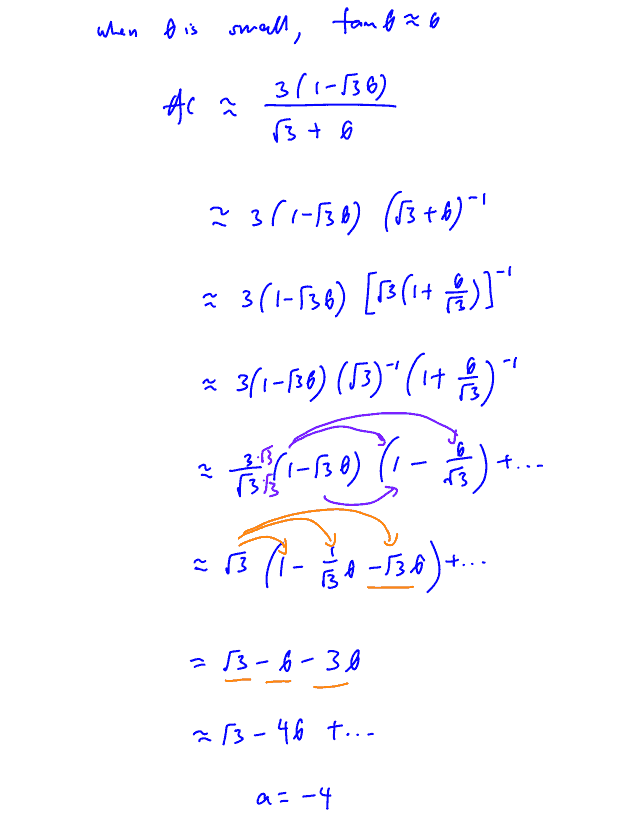
Share with your friends!
How to show ${{\text{e}}^{\text{i}\theta }}=\cos \theta +\text{i}\sin \theta $ using Standard Series
Using the standard series in MF26, show ${{\text{e}}^{\text{i}\theta }}=\cos \theta +\text{i}\sin \theta $.
Suggested Handwritten and Video Solutions
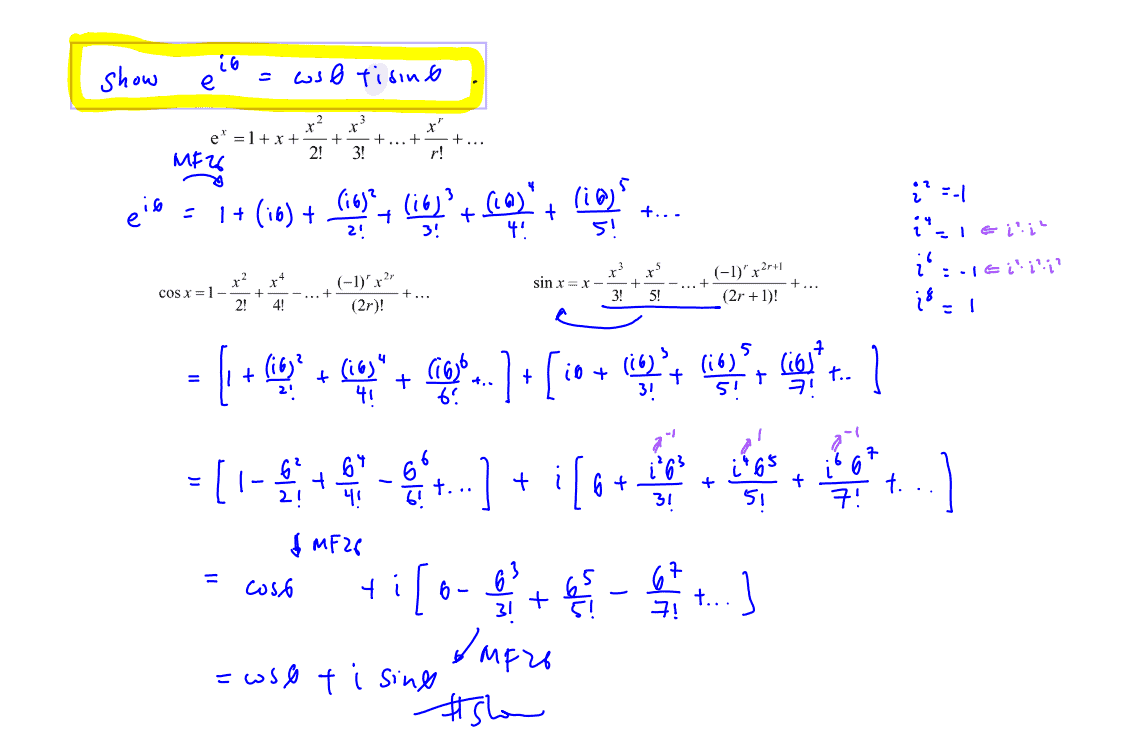
Share with your friends!
Download Maclaurin and Power Series Worksheet
Learn more about our H2 Math Tuition

H2 Math Question Bank
Check out our question bank, where our students have access to thousands of H2 Math questions with video and handwritten solutions.
Share with your friends!
