2020 NJC J2 CT1 Q2
A teacher is conducting a lesson on angles. She asks Bob to verify that the angle of elevation from a fixed point $P$ to a fixed point $A$ at the top of a building is $\theta$ radians where $0<\theta <\frac{\pi }{2}$. Instead of standing at point $P$, Bob stood at point $B$ to take the measurement, shown in the diagram below.
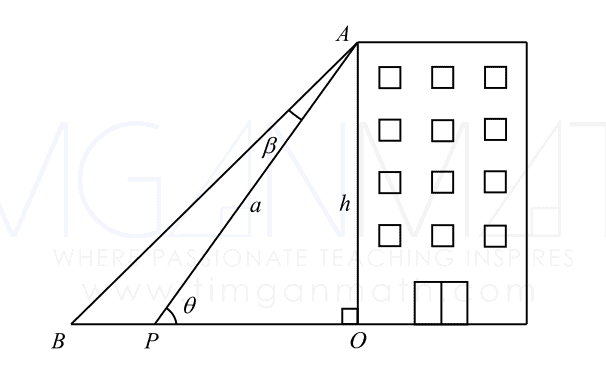
The angle $BAP$ is denoted by $\beta$. The height of the building $OA$ and distance $AP$ are fixed constants $h$ and $a$ respectively. $OPB$ forms a straight line.
(i)
Show that $AB=\frac{a}{\cos \beta -k\sin \beta }$, where $k$ is a constant expressed in terms of $\theta $.
[2]
(ii)
Given that $\beta$ is sufficiently small angle, show that
$AB\approx a\left( 1+m\beta +n{{\beta }^{2}} \right)$,
where $m$ and $n$ are constants, in terms of $k$, to be determined.
[3]
(iii)
It is further given that $k=2$. Find the set of positive values of $\beta$ for the approximation found in part (ii) to be valid, giving your answers to 4 significant figures.
[2]
Suggested Handwritten and Video Solutions
Share with your friends!